基于网络演算的多窗口分区可调度性分析
何锋,张立,于思凡,周璇
北京航空航天大学 电子信息工程学院,北京 100191
航空电子系统的发展经历了分立式、联合式、综合式、先进综合式4 个阶段,正朝着分布式综合化架构发展。ARINC 653 规范是适用于航空软件的实时操作系统接口标准,其规定了综合模块化航空电子系统(Integrated Modular Avionics,IMA)体系架构下的操作系统的行为逻辑和向应用程序提供的接口规范[1]。ARINC 653 规范定义了分区的概念,分区操作系统采用两层调度机制,分区间通过时间轮转调度的方式共享处理资源,处理任务在分区激活窗口内进行本地调度,与其他分区的任务在时间维度上相互隔离[2-3]。由于航空电子系统的高实时性要求,分区调度必须满足实时性,探寻精确的最坏延迟计算方法则是保证实时性的必要条件。当前的分区系统可调度性分析方法无法对主时间框架下具有多窗口分区的系统进行任务最大响应时间(Worst-Case Response Time,WCRT)的精确计算。因而如何能够实现多窗口分区下任务实时性的精确评估就成为当下分区调度研究的重点。
目前针对系统的可调度性分析已有多位国内外学者进行了研究。Bini和Buttazzo[4]针对单调速率调度算法从任务利用率函数的角度来分析,并给出相应的判定不等式。高晓光等[5]针对单分区任务响应时间上限的计算方法进行研究,将其他分区视为对某个分区的阻塞,推导出多分区双层调度系统下的任务响应时间上限分析方法,但该算法只有在系统任务数量较小时才有较高精度。谭龙华等[6]基于负载请求与平台资源提供能力的供需约束关系给出了系统可调度性的判定依据。Easwaran 等[7]基于资源模型分析技术,提出了考虑偏移、抖动和截止期限的可调度性分析模型。Chen 等[8]提出了一种多核处理器上分区可调度性判定方法,通过计算最大缩放因子来确定所有分区的可调度性。
这些方法基本都是从任务最坏响应时间的迭代计算或者任务负载利用率等角度实施系统的可调度性分析,同时还存在不适配一个主时间框架下分区包含多个激活窗口的最坏响应时间计算的问题。此外,对于IMA 系统的研究往往需要对计算模块和网络交换模块组成的系统架构进行综合演算分析。因此本文从网络演算的视角下对分区任务的可调度性进行分析,将计算模块和网络交换模块延迟计算模型进行统一,并发展出对任务系统可调度性分析的新思路。
网络演算是一种对网络性能分析的方法,该方法通过流量的到达曲线和端口的服务曲线之间的关系来对流量的最坏延迟进行精确计算。一方面,网络流量的传输是交换机对于流量中消息数据帧的转发;任务的执行是处理器单元对于任务包含的指令进行运算。这两者都可以抽象为对服务能力需求与对服务能力提供的关系,具有一定的相似性。另一方面,由于分区在主时间框架内的多个释放抖动窗具备服务资源的独立性,使用网络演算中的服务曲线模型,能够与每个激活窗口的具体偏置和持续时间进行匹配,可以解决传统最坏响应时间算法无法计算主时间框架下多激活窗口分区的情况。基于此,可以将网络演算的算法思想应用到任务的延迟计算中,以发展解决调度问题的新思路。
本文将适用于机载网络系统通信确定性分析的方法拓展到系统任务可调度性分析的计算过程中,创建分区和任务的网络演算模型,提出对基于固定优先级调度策略下任务的最大响应时间计算计算方法,发展实现任务调度演算乃至IMA 系统性能一体化演算的新思路。
1 系统模型
1.1 分区任务调度模型
ARINC653 分区操作系统采用两层调度策略。在操作系统层,上层调度器采用轮转调度的方式执行每一个分区;在每个分区内部,下层调度器根据设计的任务调度策略进行任务调度,分区内的任务只有在所属分区处于执行状态时才有机会被执行。分区调度具有严格的确定性,每个分区都有自己的周期和窗口时间,分区基于周期时间序列进行计算资源的确定性分配,并按照主时间框架分配给它的时间窗口依次激活执行。任务在分区内进行调度执行,任务之间根据调度策略进行调度运行。分区内任务调度策略主要包含固定优先级调度策略和动态优先级调度策略,本文主要探讨单核系统固定优先级抢占式调度下的任务可调度性分析问题。对于多核系统分区调度的情况可以简化为多个单核系统[9]。
考虑单处理器系统,系统包含有K个分区,每个分区可以用Pk(1 ≤k≤K)来表示,分区属性可由〈周期Tk,窗口时长Lk〉两元组合来表示。系统对K个分区采用轮转调度策略来进行访问执行,主时间框架TRL为所有分区周期的最小公倍数。分区内包含nk个任务,任务集合为Γk={τki|1 ≤i≤nk},所有任务都为周期任务,任务之间相互独立。任务τki可由〈释放抖动Jki,周期Tki,计算时间Cki,截至期限Dki,优先级Oki〉五元组合来表示。系统对分区内的任务集采用固定优先级调度策略进行调度,任务之间允许抢占。系统中分区任务的调度模型如图1 所示。
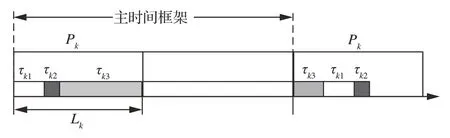
图1 分区任务调度模型Fig.1 Scheduling model of partitions and tasks
1.2 网络演算模型
网络演算是对网络性能进行定量分析的一种基于最小加代数的排队理论。网络演算可以分为确定性网络演算[10-11]和随机网络演算[12-13]2 类,本文将重点讨论确定性网络演算模型。确定性网络演算的基本思想是利用替换代数,即最小加代数和最大加代数的数学演算理论,把复杂的非线性系统转换为简单的线性系统,将网络中的节点作为建模的目标,通过对流经节点的数据流的排队计算,实现整个网络性能的分析。
确定性网络演算中定义到达曲线α(t)[14-15]来表示到达数据的上包络,定义服务曲线β(t)[16-17]来表示某一节点对于数据流的最小服务能力,到达曲线和服务曲线的最大水平截距h(α,β)表示数据流在该节点的最坏延迟dmax,最大垂直截距v(α,β)表示数据流在该节点的最大数据积压wmax[18],σ为突发度,T为技术延迟,如图2 所示。

图2 确定性网络演算模型Fig.2 Deterministic network calculus model
确定性网络演算被广泛应用于航空网络系统确定性分析中[19],其中包括对于时间触发以太网(Time Triggered Ethernet,TTE)的实时性分析。时间触发以太网在以太网的基础上添加了全局时钟同步机制和时间触发机制。TTE 包含时间触发(Time-Triggered,TT)、速率约 束(Rate-Constrained,RC)、尽力传输(Best-Effort,BE)3 种不同类型的流量,其中TT 流量的传输具有严格的周期性和确定性[20]。TT 流量按照离线设计好的固定时刻进行发送,网络中的节点对于TT流的转发时刻也是离线设定。TT 流量具有严格周期性的特点,其到达曲线模型和服务曲线模型也与RC 流量、BE 流量有所不同。图3 给出了单个TT 流的到达曲线和服务曲线以及最坏延迟时间,其中,lTT为TT 流量的数据帧长;pTT为TT 流量的周期;Dmax为最坏延迟时间。
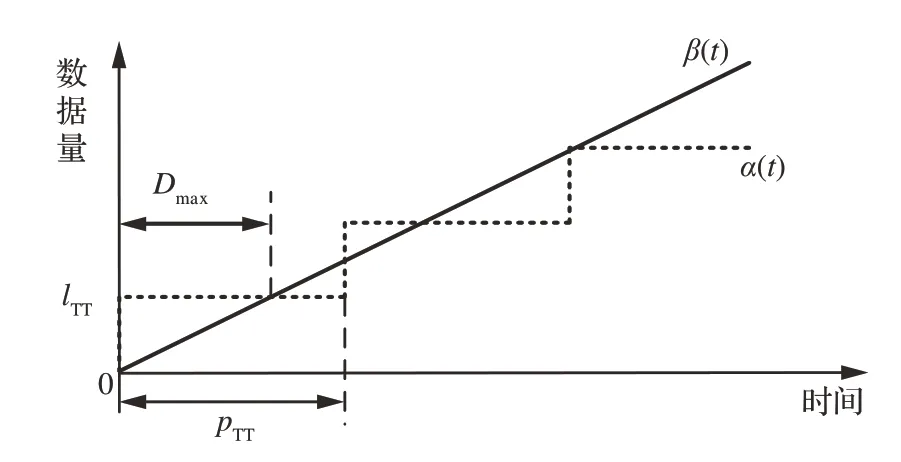
图3 TT 流到达曲线和服务曲线Fig.3 Arrival curve and service curve of a TT flow
2 任务可调度性分析
流量的传输是交换机对输入流量提供服务的过程,本质上是服务需求和服务能力之间的关系,通过分析这两者之间的关系可以计算流量的延迟。而任务的执行也可以看作是处理器单元为任务提供服务的过程。对于任务,其对计算的需求可以表示为任务需求函数,如考虑一段时间内(通常为周期),任务需要得到处理器完成的计算量。借助于网络演算中到达曲线的定义,可以将这种计算的需求看作是任务处理需求的一种到达模型。因此,可以定义任务的到达曲线为任务对计算资源的需求函数;定义平台对任务的服务曲线为处理平台对该任务所能提供计算资源的服务能力,由此可以借助网络演算的理念发展任务最大响应时间计算方法。
定义1 对于某一任务τki,设αki(t)为任务τki的到达曲线函数,βki(t)为处理平台对τki提供的服务曲线函数,那么任务τki的最大响应时间Wki为αki(t) 与βki(t) 的最大水平截距,即h(αki(t),βki(t))。
证明 考虑一周期性任务τki,该任务对计算资源的需求会随着任务周期性的到达而递增,系统对任务τki所提供的计算资源随时间呈非递减,所以任务的到达曲线和服务曲线都是非递减函数。
若任务到达曲线和服务曲线不相交,那么任意时刻t必有αki(t)>βki(t),此时系统不可调度。
若任务到达曲线和服务曲线相交,那么两曲线的交点即为任务需求与系统提供服务能力的平衡点。在平衡点之前,假设任务τki的p次到达时刻为,则任务到达时刻对计算资源的需求为,假设在时刻,满足,即系统在时刻所提供的服务恰好满足任务在时刻所需求的服务,则任务第p次到达时的响应时间为假设平衡点之前任务到达N次,则任务的最大响应时间为这N次到达的响应时间最大值,即

因此任务的最大响应时间即为任务到达曲线与服务曲线的最大水平截距。
2.1 分区任务到达曲线模型
考虑操作系统的整体服务能力,假设处理器的处理速率为V,单位为每秒百万指令(MIPS),从整个系统来看,其服务曲线可定义为

系统总服务曲线如图4 所示。
图4 系统总服务曲线Fig.4 Service curve of system
2.1.1 分区到达曲线模型
按照ARINC 653 规范中分区调度的特点,分区在主时间框架中进行具有严格周期的轮转调度。考虑一分区Pk的周期为Tk,时间窗口长度为Lk,假设其第1 次到达时刻为Ak,那么该分区的调度时刻如图5 所示。
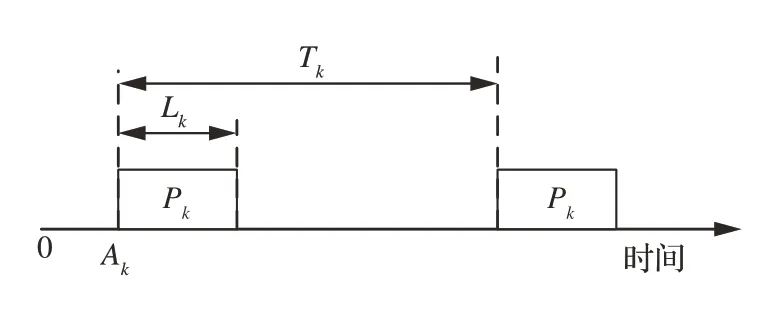
图5 分区调度时刻Fig.5 Partition scheduling timeline
分区Pk在操作系统上的到达是1 个周期为Tk的过程,其到达曲线可由阶梯函数给出

分区到达曲线如图6 所示。
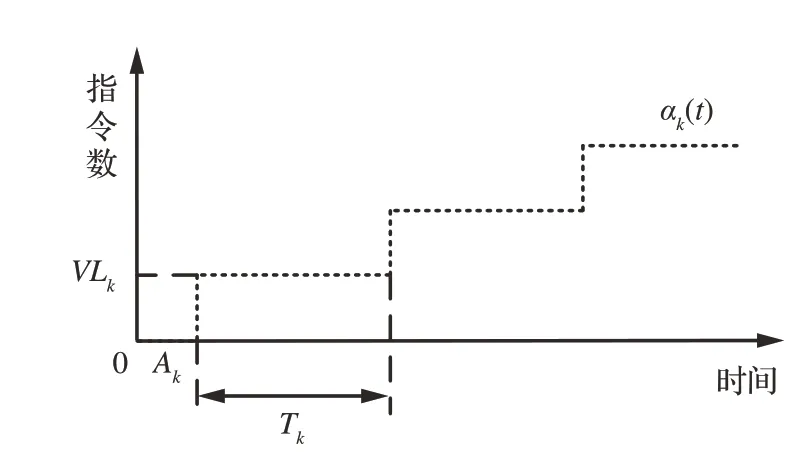
图6 分区到达曲线Fig.6 Arrival curve of partition
证明 对于任意时间间隔[s,t),在操作系统上共有nk(s,t)个分区Pk的时间窗口,有

假设使用Rk(t)表示分区Pk在操作系统上的到达过程,则有

根据网络演算中关于到达曲线与流量累计曲线的定义可知,分区Pk在操作系统上的到达曲线为,其中t>0。
2.1.2 任务到达曲线模型
考虑一分区Pk内的任务τki,其周期为Tki,任务执行时长为Cki,假设第1 次到达时间为Aki,从分区到达曲线的模型可以类似推出任务τki的到达曲线模型,如图7 所示。
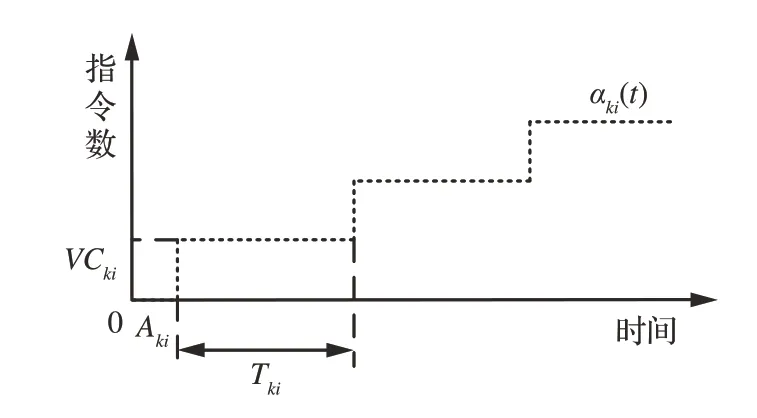
图7 任务到达曲线Fig.7 Arrival curve of task
参考分区到达曲线函数的证明过程,可以类似得出任务的到达曲线函数
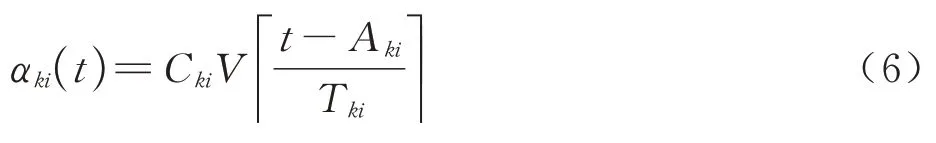
2.2 分区任务服务曲线模型
2.2.1 分区服务曲线模型
在ARINC653 规范中,操作系统对于分区采用轮转调度策略,所以对于分区Pk的服务则为系统所提供的总服务能力减去对其他分区占用窗口后的剩余服务。考虑到主时间框架中的空闲时间部分并不能为其他分区提供服务,所以可以将主时间框架中的空闲时间段看作是周期为TRL的空闲分区,在计算分区服务曲线时减掉。分区Pk的服务曲线为
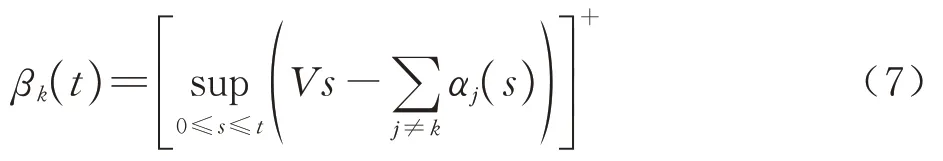
式中:V为处理器速率;sup 为取上确界。
证明 假设使用Rk(t)表示分区Pk的累计服务函数,令s表示忙周期的起始位置,在忙周期[s,t)内其他分区的总的服务为
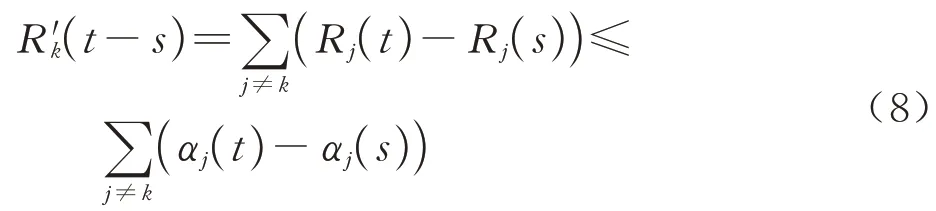
式中:αj(t)为分区Pj的到达曲线。
在忙周期[s,t)内对于分区Pk的服务为总服务能力减去对其他分区Pj的服务,即

又由于Rk(t)为广义增函数,因此有
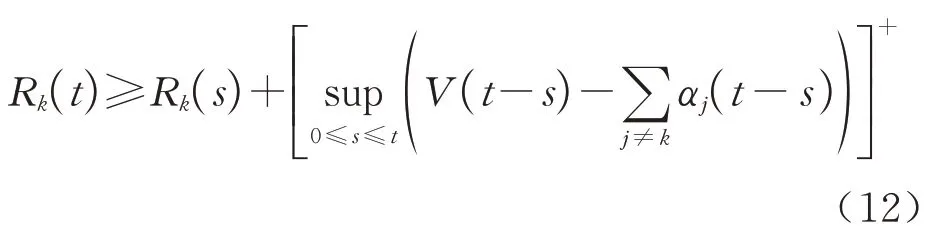
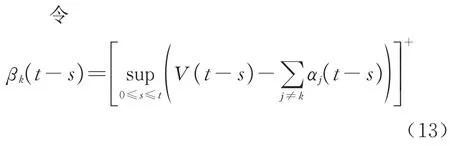
则式(12)可简化为
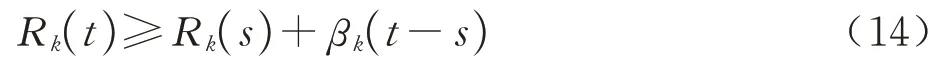
依据最小加代数卷积定义有
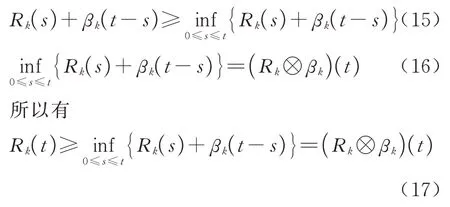
式中:⊗为极小加代数中的卷积运算;inf 为取下确界。
根据网络演算中服务曲线与累计服务曲线的定义可知,分区Pk在操作系统上的服务曲线为,分 区Pk的服务曲线如图8 所示。

图8 分区服务曲线Fig.8 Service curve of partition
2.2.2 任务服务曲线模型
考虑下层调度器采用固定优先级调度策略对分区内的任务进行调度,因而对于分区内任务τki的服务曲线为分区所提供的总的服务能力减去优先级高于τki的任务τkj(Okj<Oki)后的剩余服务
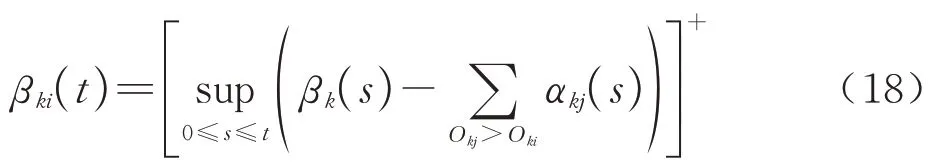
式中:Oki为任务τki的优先级。
详细证明可以参考对分区服务曲线的证明过程。任务τki的服务曲线与分区Pk的服务曲线如图9 所示。
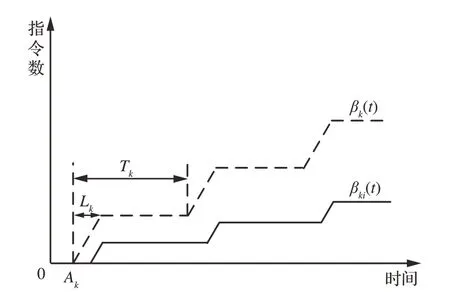
图9 分区和任务服务曲线Fig.9 Service curves of partition and task
2.3 任务可调度性判定
任务的可调度性分析可根据任务的最大响应时间Wki和任务截止期限Dki的关系来进行判定,若任务τki的最大响应时间Wki满足Wki≤Dki,则任务可调度。任务可调度性分析转化为求任务的最大响应时间问题。任务的最大响应时间依据定义1 可以通过任务的到达曲线和服务曲线的最大水平截距h(αki,βki)计算得到。
对于任务τki,其最大响应时间的发生条件为τki的任务实例与分区Pk内所有其他任务实例在同时刻释放,并且刚好错过其所在分区的调度窗口,基于此来计算任务τki的到达曲线和服务曲线。算法1 给出了计算任务最大响应时间的伪代码。
3 案例分析
设计2 个包含若干分区和任务的系统案例,对本文提出算法的计算结果和优缺点进行验证分析。
案例1 验证本文提出的网络演算视角下的最坏延迟分析具有与传统通过迭代方式进行最坏响应时间分析的同等精度。

假设系统提供的总处理速率V为1 000 MIPS,系统共包含5 个分区以及1 个空闲时间分区,分区的参数信息如表1 所示。
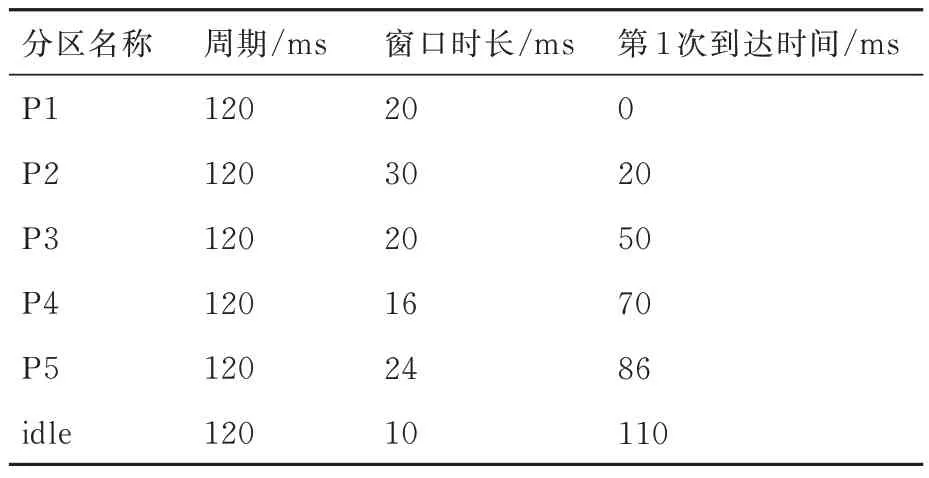
表1 案例1 分区参数Table 1 Parameters of partitions in Case 1
主时间框架的长度为所有分区周期的最小公倍数[6],结合表1 的分区参数信息,可以得出主时间框架的长度为120 ms,在主时间框架中,各分区的调度时刻如图10 所示。
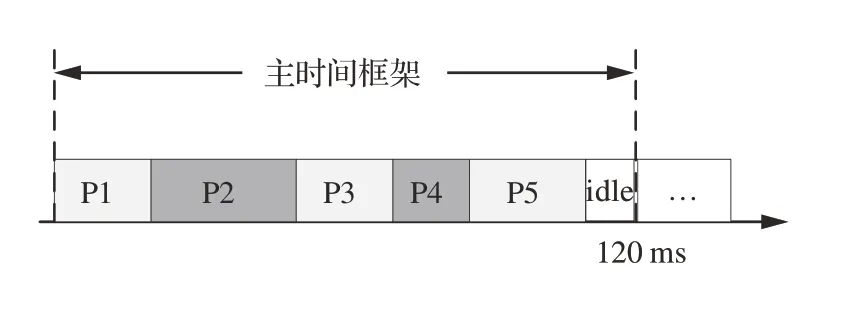
图10 主时间框架中各分区窗口Fig.10 Partition windows within a main frame
系统中分区包含的任务信息如表2 所示,所有任务的释放抖动为0,截止期限Dki等于任务周期Tki,忽略分区任务切换开销。
使用MATLAB 中的rtc 工具箱对表2 中的分区和表3 中的任务参数信息进行建模,并生成分区和任务的到达曲线。任务到达曲线如图11所示。
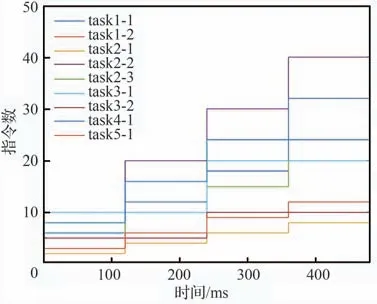
图11 任务到达曲线Fig.11 Arrival curves of tasks
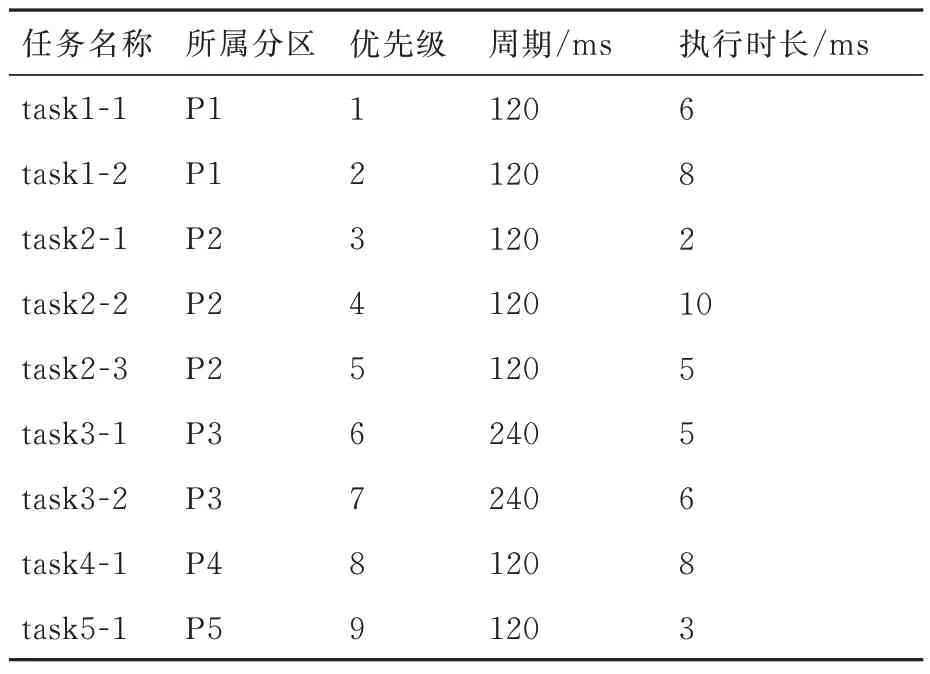
表2 案例1 任务参数信息Table 2 Parameters of tasks in Case 1
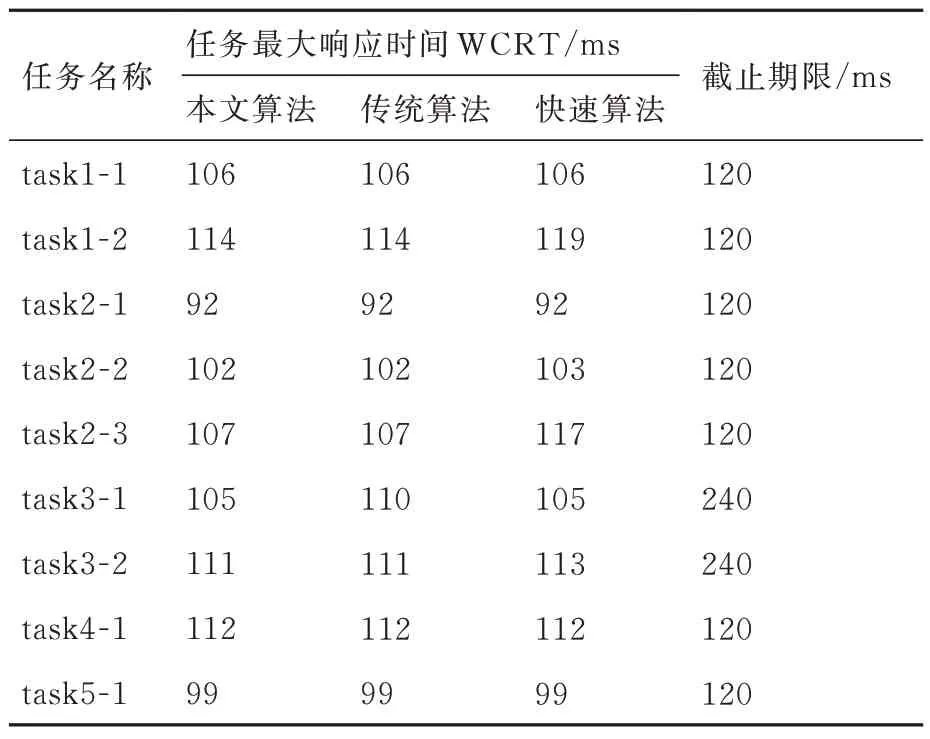
表3 案例1 所有任务的最大响应时间Table 3 WCRT for all tasks in Case 1
以任务task2-2 为例,计算任务的最大响应时间。对于任务的最大响应时间计算条件为分区内所有任务均在同一时刻到达,且刚好错过分区窗口。假设所有任务均在0 时刻到达,那么任务分区窗口将在Tk-Lk后到达。根据各分区到达曲线计算利用式(7)、式(18)可以计算得到任务task2-2 的服务曲线,task2-2 的最大响应时间即为task2-2 的到达曲线和服务曲线的最大水平截距,如图12 所示。
从图12 可得task2-2 的到达曲线和服务曲线的最大水平截距为102,也即task2-2 的最大响应时间102 ms,小于截止期限120 ms,task2-2 可调度。与任务实际执行情况是一致的。对系统中所有任务的最大响应时间使用本文算法进行计算并与文献[21]所提出的精确计算任务最大响应时间的传统算法、文献[5]提出的响应时间上限快速算法的计算结果进行比较,结果如表3所示。
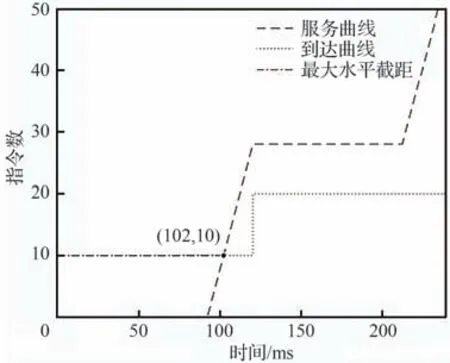
图12 到达曲线和服务曲线最大水平截距Fig.12 Maximum horizontal intercept between arrival curve and service curve
文献[21]所提出的传统算法公式为
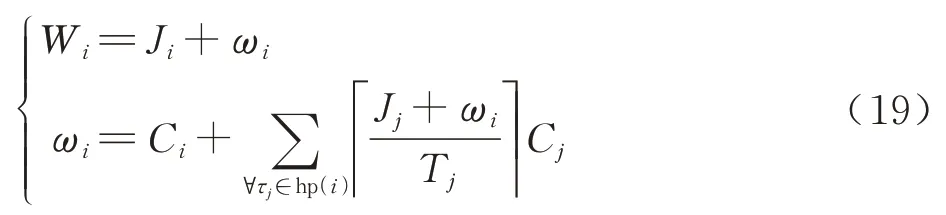
式中:Wi为任务τi的最大响应时间;Ji为释放抖动;Ci为任务执行时长;Ti为任务周期;hp(i)为优先级高于τi的任务集合。
文献[5]所提出的响应时间上限快速算法公式为

式中:Wki为任务τki的最大响应时间;Cki为任务执行时长;TRL为主时间框架长度;ηk为分区的执行系数。
通过表3 可以发现,本文提出的算法与传统算法具有相同的精确度,相较于文献[5]提出的响应时间上限快速算法具有更加紧凑的边界。
案例2 在主时间框架下分区有多个激活窗口的情况下,验证任务的可调度性分析。
假设系统条件与案例1 相同,修改分区参数信息如表4 所示。从分区参数信息可以看出,主时间框架为240 ms,P1、P2、P5在1个主时间框架内有2 个调度窗口,而P3,P4 在主时间框架内有一个调度窗口,在主时间框架中,各分区的调度时刻如图13所示。任务参数信息如表5 所示。

图13 主时间框架中各分区窗口Fig.13 Partition windows within a main frame
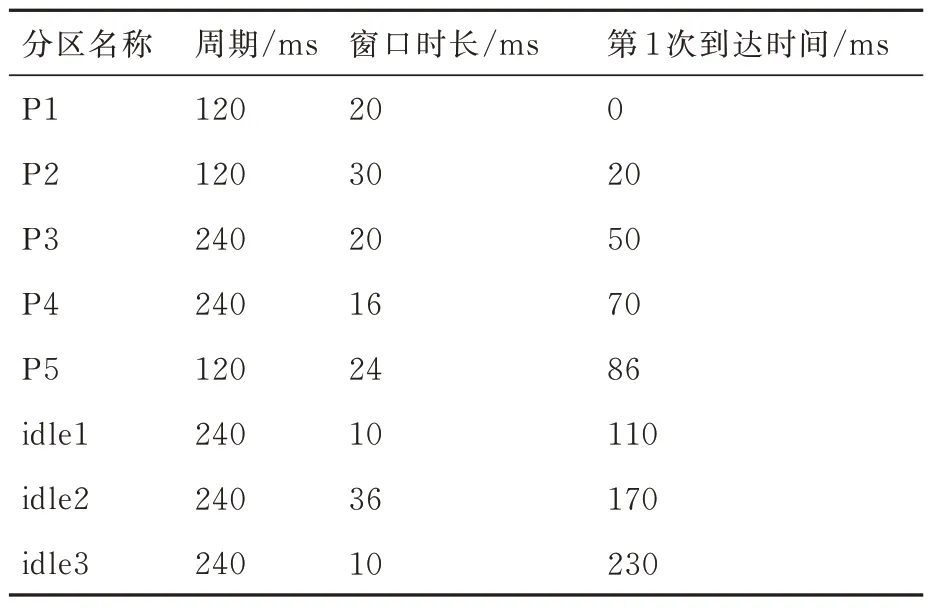
表4 案例2 分区参数Table 4 Parameters of partitions in Case 2
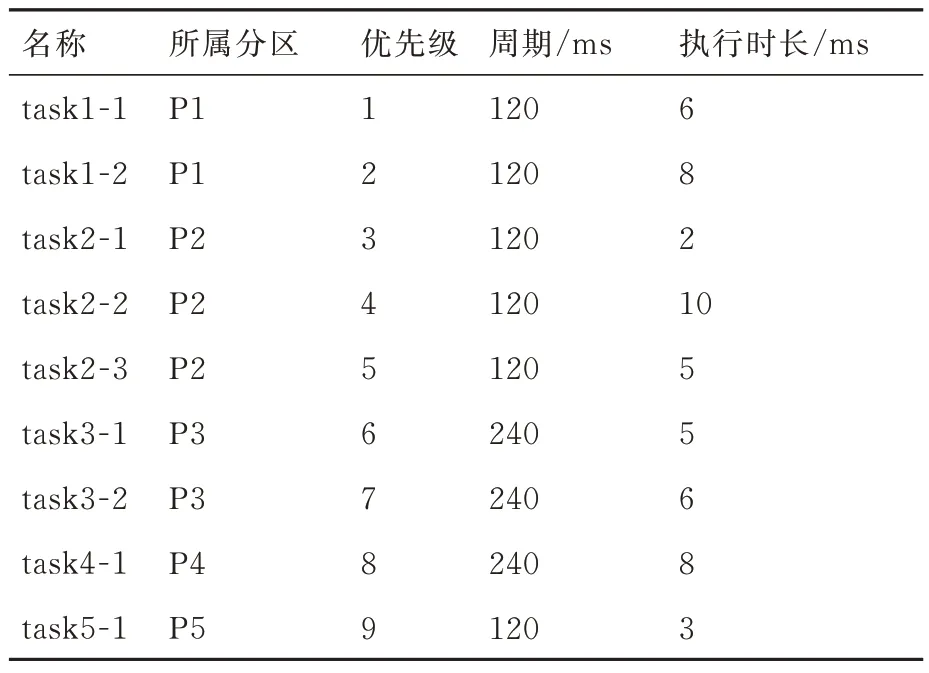
表5 案例2 任务参数信息Table 5 Parameters of tasks in Case 2
按照案例1 计算过程,分别使用本文算法、文献[21]的传统算法、文献[5]的快速算法,计算各任务的最大响应时间,如表6 所示。
从表6 可看出3 种方法对主时间框架中只有1 个窗口的单窗口分区(P3、P4)内任务的WCRT计算结果是比较接近的,其中本文方法与传统方法计算结果相同,比文献[5]的快速算法更准确,但对多窗口分区的计算结果相差较多。文献[21]的传统算法和文献[5]的快速算法将其他分区视为最高优先级任务对本分区内任务的阻塞,这就会在计算时将多窗口分区的多个窗口合并,导致计算结果远大于实际结果,而基于网络演算的最大响应时间算法解决了这一问题。
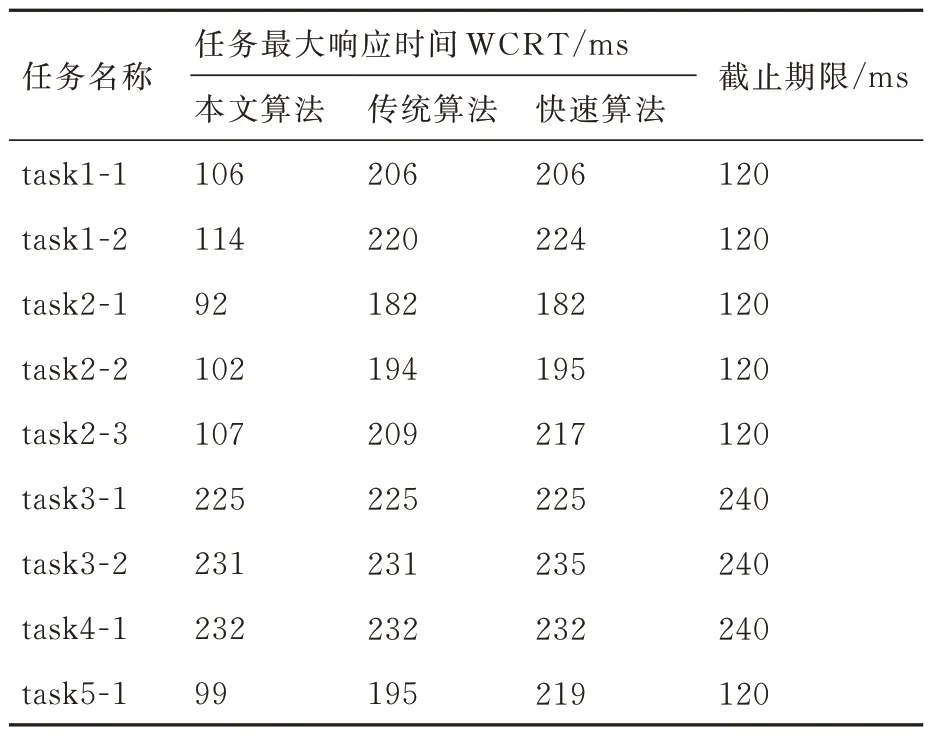
表6 案例2 任务的最大响应时间Table 6 WCRT of tasks in Case 2
4 结论
1)针对ARINC653 规范的分区操作系统的任务可调度判定问题,提出了一种基于网络演算思想的可调度性判断方法。通过实验分析表明,该方法能够对分区任务两层调度模型下任务的最大响应时间进行精确计算,计算结果的精确度与传统的任务最大响应时间算法相同,为任务可调度性判定提供了数据基础。
2)该分析方法将航空电子系统的网络传输系统延迟计算模型和处理系统延迟计算模型进行了统一,使用一套计算模型即可完成对消息的端到端、任务到任务之间的延迟进行精确计算。其能够计算分区在主时间框架中有多个激活窗口的情况,弥补了当前可调度分析算法在这一方面的不足。后续将进一步优化算法的时间复杂度。

