基于旋转搜索的相机位姿估计和对应点匹配

王平，付辉，徐贵力

1.兰州理工大学 电气工程与信息工程学院，兰州 730050

2.甘肃省工业过程先进控制重点实验室，兰州 730050

3.南京航空航天大学 自动化学院，南京 210016

基于视觉的位置和姿态（简称位姿）估计问题又称为n点透视成像（Perspective-n-Point，PnP）问题。该问题是在相机内参数已知的情况下，利用n个3D 空间已知的特征点和其对应的2D 图像点来估计相机和目标之间的位姿参数。PnP 问题的解决可广泛应用于视觉导航［1］、目标位置和姿态的监测［2］、无人机的视觉着陆［3］、航天器的自主交会对接［4］等领域。

目前，PnP 算法的研究已经取得了丰硕成果［5-13］。然而，PnP 问题中需要知道3D 空间特征点与其2D 图像点的对应匹配关系，这是PnP 问题能够准确求解的必要条件。在一些实际应用中，可以通过人工的方式寻找3D 物点与2D 像点的匹配关系［14］，但这无法满足实时且自主估算位姿的要求。为了解决以上问题，可以在3D 空间按照一定规则编码目标（即物点）［15］，然后通过图像处理的方法提取编码信息，确定相应的3D 物点和2D 像点对应匹配关系。然而，采用图像编码方式识别3D/2D 对应匹配关系的方法容易受到成像质量的影响，空间目标成像不清晰或图像存在较大畸变时，将无法从图像中正确识别出编码信息，进而导致3D/2D 对应点匹配失败。为克服采用图像识别方式匹配3D/2D 对应点方法的缺点，David 等［16］提出了一种可以实现同步位姿估计和对应点匹配（Simultaneous Pose and Correspondence Determination，SPCD）的 Soft-POSIT 算法。该算法基于弱透视成像模型，同时结 合Softassign［17］和POSIT（Pose from Orthography and Scaling with Iterations）［18］2 种算法，采用交替迭代的方式实现估算位姿的同时确定对应点匹配关系。张鑫等［19］、劳达宝等［20］对Soft-POSIT 算法进行了应用研究，表明SoftPOSIT算法局部收敛能力好，但无法全局收敛。为了提升SoftPOSIT 算法的抗噪能力，Moreno-Noguer等［21］提出了BlindPnP 算法。该算法采用混合高斯模型建模姿态集，并将其用来初始化算法中的卡尔曼滤波器。存在大量噪声的情况下，Blind-PnP 算法性能优于SoftPOSIT 算法，在常规情况下性能和SoftPOSIT 算法相当，且都无法收敛于全局最优值。为了得到SPCD 问题的最优解，Brown 等［22-23］提出了BnBDA 算法，该算法将SPCD 问题转换为优化问题，并采用分支定界的方法在旋转和位置空间上交替搜索位姿参数的最优值。基于以上思路，Campbell 等［24］在随后的工作中研究了空间存在孤立点时的SPCD 问题。最近的工作中，Liu 等［25］基于分支定界的思路，研究了基于直线特征的同步位姿估计和对应直线匹配问题，取得了良好的效果。

相比于SoftPOSIT 算法，采用分支定界思路解决SPCD 问题的方法可以在全局空间上得到最优解，因此收敛率和精度都较高。然而，分支定界方法求解时需要预先给定旋转和位置参数的搜索空间。对于旋转参数，利用欧拉角表示时取值范围为[-π，π]。而对于位置参数，实际问题中的初始位置往往是无法确定的，为了保证搜索到较为准确的位置值，通常需要给定一个很大范围，这增加了分支定界迭代搜索的复杂度，影响了效率，限制了这类算法的实际应用。事实上，在SPCD 问题中，除了3D/2D 点特征可以提供约束信息构建优化函数以外，点和点之间也可以提供约束信息，但现有算法中都未曾考虑这些信息。基于以上思路，本文在SPCD 问题中引入点和点之间的约束模型，该约束模型中仅含有旋转参数。并基于以上约束模型，从几何意义上出发构建优化求解SPCD 问题的目标函数，采用分支定界的方式在旋转空间上搜索最优旋转参数和最佳3D/2D 匹配对应关系，以高精度实现相机同步位姿估计和对应点匹配。

1 SPCD 问题描述

如图1 所示，相机内参数标定的情况下，在3D 空间给定一组世界坐标已知的空间目标参考点P={Pi|i=1，2，…，m}，其在2D 图像上的投影点 为p={pj|j=1，2，…，n}，并且P和p之间的一一对应关系未知。SPCD 问题就是在计算相机位姿（即旋转矩阵R∈SO(3)和平移矩阵t∈R3）的同时来确定P和p之间的对应关系。在一些位姿估算任务中，如点云匹配［26］，由于目标遮挡的原因，目标参考点集P和其2D 投影点集p的大小不相等，即m≠n。但在大多数视觉位姿任务中，P和p的大小是相同的，即m=n。基于相机透视成像模型［8］，SPCD 问题可以表示为

图1 SPCD 问题描述Fig.1 Description of SPCD problem

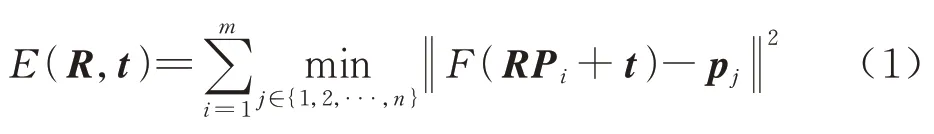
式中：F(·)为相机坐标系下3D 参考点到2D 图像点的投影变换。SPCD 问题的本质就是在3D 特征点和2D 投影点对应关系未知的情况下，寻找最优的R*、t*使得式（1）的误差最小。在误差最小的情况下，通过估算位姿R和t反向重构的模型能够和原始模型实现最佳的匹配。

2 基于点对点约束SPCD 问题求解

2.1 点对点约束模型推导

现有的SoftPOSIT 算法［14］或优化求解SPCD 问题的方法［20-22］都是以式（1）误差最小为思路求解。从式（1）中可以看出，求解过程中涉及的变量有R和t，因此迭代优化过程中需要对R和t交替求解，无疑增加了算法实现的复杂度。除此之外，旋转R和平移t自身的量纲不同，同时优化求解时容易造成算法的不稳定。事实上，在求解SPCD 问题时，除了3D/2D 点特征可以提供约束外，点和点之间也可以提供约束信息，现有的算法中并未有效利用这些点和点之间的约束信息。基于以上思路，本文提出一种基于点和点之间约束信息，并从几何意义上构建优化目标函数求解SPCD 问题的方法。

如 图2 所 示，Pi，Pj∈P为3D 空间中 的任意2 点，假设其对应图像平面上的投影点为pi，pj∈p。相机光心O和pi、pj共同形成一平面，其平面法向量为Nij。当相机内参数标定的情况下，Nij可以很容易由O和pi、pj形成的向量得到

利用旋转矩阵R和平移向量t可以将世界坐标系下的Pi、Pj转换为相机坐标系下的Ci、Cj，转换关系为

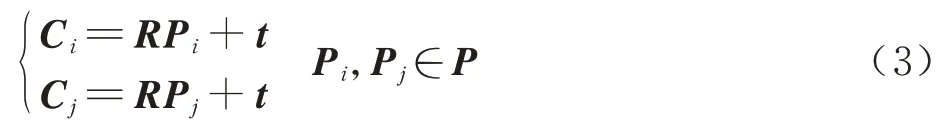
式（3）中上下两式相减，得

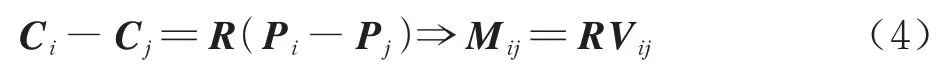
式中：Mij为相机坐标系下的向量，且在平面OCiCj内。从图2 可以看出，Opi pj、OCiCj为同一个平面，因此Nij与Mij互相垂直，即Nij与RVij之间的夹角为。对于空间目标参考点集P，按式（4）的定义可以生成个关于V的方向向量V={Vx|x=1，2，...，K1}。同理，投影点集p可按照式（2）生成平面法向量集合N={Ny|y=1，2，...，K2}，其中。由于P和p的对应关系未知，因此生成的V和N对应关系也未知。此时，基于新生成的方向向量集合V和法向量集N，SPCD 问题可以转换为如下优化问题：

图2 点对点的约束Fig.2 Point-to-point constraint

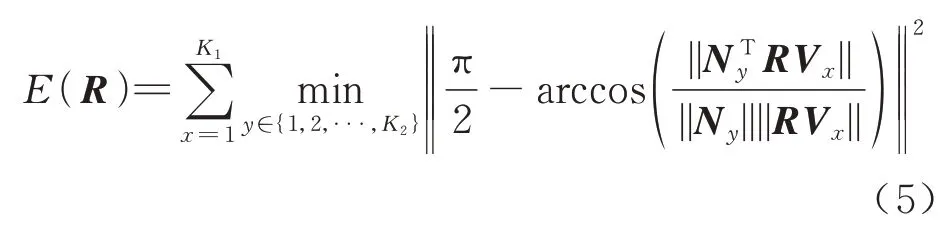
式中：arccos(·)为反余弦函数，表示Ny和RVx的夹角，||NyTRVx||则限定了该夹角为锐角。当3D参考点生成的方向向量V与其2D 投影点生成的平面法向量N一一对应，且计算的姿态参数R*最优时，式（5）误差最小。相比于式（1），式（5）中仅含有旋转参数R待求解，形式上更为简单且待求解参数量纲唯一，能够有效提升求解SPCD 问题时收敛到全局最优解的概率，并且在优化求解时更容易实现。由于R是一个旋转矩阵，具有正交性。当Ny和Vx单位化的时候，||Ny||||RVx||=1，此时式（5）可以简化为

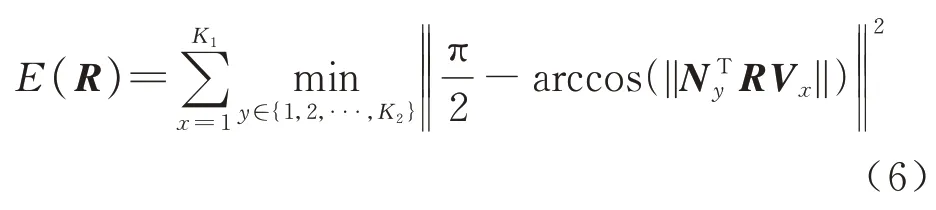
2.2 目标函数上界和下界确定

分支定界法能够在变量取值空间上迭代搜素全局最优值且不会陷入局部最优，因此本文采用分支定界的方式求解式（6）的最优值。采用欧拉角r=[α，β，γ]表示旋转R

式中：α、β、γ的取值范围为-π～π，因此r=的取值空间形成半径为π 的球体，如图3（a）所示。为了在分支定界过程中取值空间的划分方便，将r=[α，β，γ]的取值空间从半径为π 的球体扩充为半径为π 的立方体，记作Cr。对式（6）分支定界的过程，就是对Cr按照3D 八叉树结构不断迭代划分使得式（6）误差最小的过程，在这一过程中需要确定式（6）在每个划分子空间的上界和下界

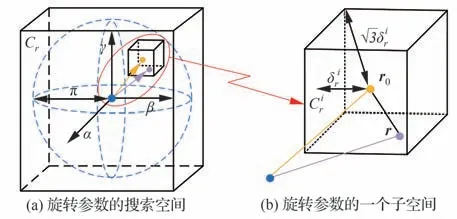
图3 旋转参数几何边界的表示Fig.3 An illustration of geometric bounds of rotation parameters

对于式（6）下界的推导，需要使用到文献［27］中的引理。

引理1 采用欧拉角的形式给定2 个旋转r、r0，其对应旋转矩阵为R(r)、R(r0)，则对于空间任意向量Vx∈R3，都存在不等式关系

式中：∠(·，·)为两向量的夹角。

综合式（9）、式（10）可以得出

式（6）在分支定界过程中主要计算Ny与R(r)Vx的夹角，即∠(Ny，R(r)Vx)，利用三角不等式的关系可以得到

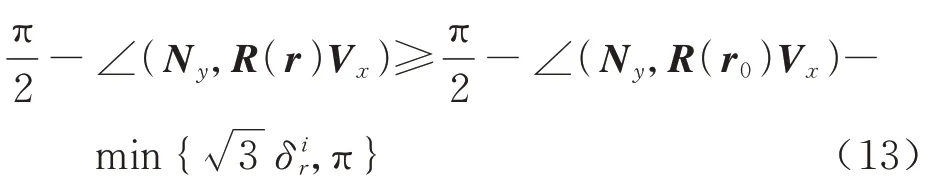
式（13）两端取模代入式（6），最终得到式（6）在子空间上的下界

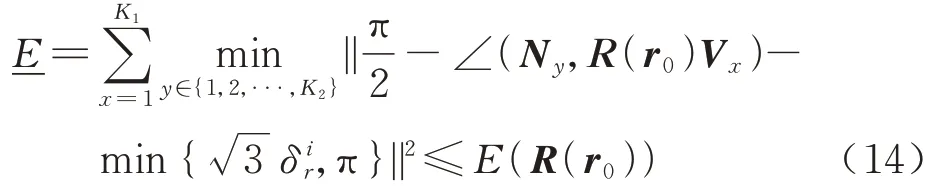
式中：∠(Ny，R(r0)Vx)可以由计算得到。

2.3 分支定界优化求解位姿参数

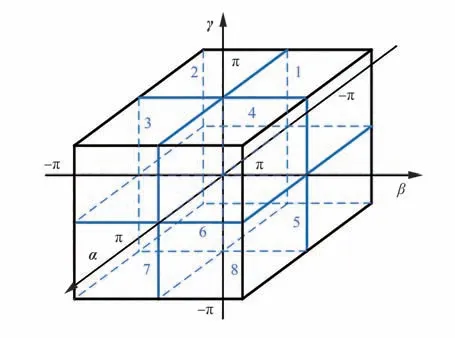
图4 一个划分子空间Fig.4 A branched subspace

根据式（6）的定义，得到最优旋转R*的同时也得到了V和N之间的最佳匹配关系。假设总共得到了k对匹配关系，从图2 可以看出，当Vij∈V和Nij∈N匹配时，Pi和Pj的中点同样垂直于Nij。记Pi和Pj的中点为，则有

将式（15）展开，进一步写为关于t的表达式

式（15）、式（16）对k对匹配关系都满足，因此有

3 实验分析

将本文提出的方法命名为BnB-P2P 算法，并采用仿真和真实实验验证的方法与SoftPOSIT算法［14］进行对比。为了测试公平，所有代码都采用MATLAB2018a 实现，本文实验代码可以从https：//github.com/pingwangsky 下载。

3.1 仿真实验

合成焦距f=800 像素，分辨率为640×480像素的虚拟相机。在相机坐标系下随机产生3D空间参考点，分布在［-2，2］m×［-2，2］m×［4，8］m 的范围内。旋转矩阵R按照式（7）生成，平移向量t取相机坐标系下3D 参考点的平均值。由于相机拍摄时目标物体在相机前方，因此式（7）中的角度r=[α，β，γ]取值在的 范围。利用生成的R、t将相机坐标系下的3D 参考点转换到世界坐标系下，得到世界坐标系下的3D参考点集P。采用合成的虚拟相机，将P投影到2D 图像上，得到其投影点集合p，并随机打乱P与p的对应匹配关系。

3.1.1 收敛成功率

SoftPOSIT 算法对初值的选取比较敏感，初值选择不合理将导致SoftPOSIT 算法无法收敛。设r=[α，β，γ]为仿真时生成的真值，SoftPOSIT算法的初始值分别在范围内选取。对于本文提出的BnB-P2P算法，由于其可以全局寻优，初始值范围只影响收敛速率，不影响最终收敛结果，因此初始值范围直接选取。改变测试点的数目从4～10，每个点处程序执行50 次，分别统计Soft-POSIT 算法、BnB-P2P 算法的收敛成功率，结果如图5 所示。

从图5 中可以看出，随着点数目的增加，Soft-POSIT 算法能够收敛的次数逐渐增加，这是由于点数目增加时提供的有效约束信息也随之增多，因此SoftPOSIT 算法能够收敛的概率随之增大。但随着初始角选取范围的扩大，SoftPOSIT 算法能够收敛的次数减少，即使点数目增加时也不能保证其完全收敛。相比之下，由于本文提出的BnB-P2P 算法采用了全局寻优的方式，在以上测试情况下的收敛成功率均可达100%，远高于SoftPOSIT 算法。

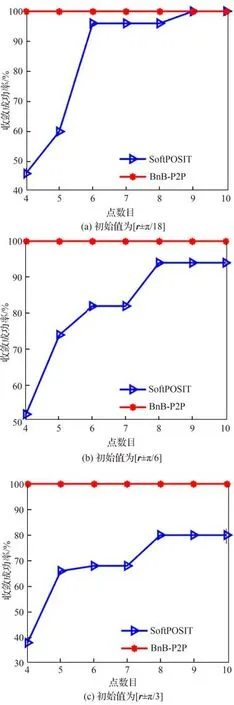
图5 收敛成功率Fig.5 Success rate of convergence

3.1.2 求解精度

算法收敛成功并不能保证算法收敛到正确的结果，为此需求取第3.1.1 节中收敛成功的结果与仿真真值之间的误差，并计算误差的平均值，旋转矩阵、平移向量的误差分别如图6 和图7所示。值得注意的是，为了误差评估的统一性，本文误差计算公式采用文献［8，11-13］中的表示形式。即

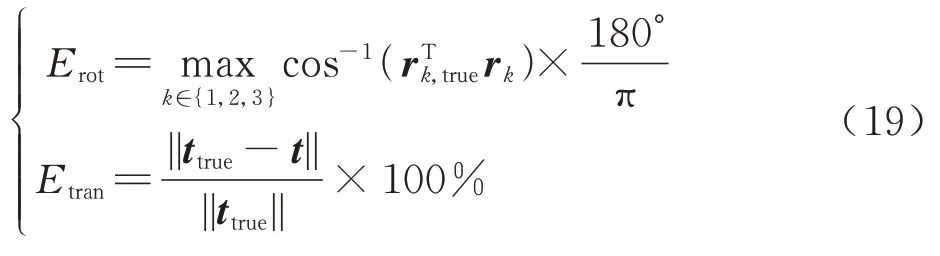
式中：Erot、Etran分别为旋转矩阵误差、平移向量误差；rk，true、rk分别为旋转矩阵真值和计算得到旋转矩阵的第k列；ttrue、t分别为平移向量真值和计算得到的平移向量。

从 图6 和 图7 可以看出，SoftPOSIT 算法虽然能够收敛成功，但是并不能保证每次都收敛到正确的结果，因此误差均值波动较大。本文提出的BnB-P2P 算法将SPCD 问题转换为了最优化问题，并且采用分支定界的方法在整个旋转空间上搜索，因此能够保证搜索到全局最优值，可靠性和准确率远高于SoftPOSIT 算法。进一步做出BnB-P2P 算法旋转矩阵误差和平移向量误差的箱型图，如图8 所示（由于SoftPOSIT 算法误差波动太大，无法绘制其箱型图）。从图中可以看出，BnB-P2P 算法平均误差数量级在10-4以内，并且波动范围不大，收敛可靠性远高于Soft-POSIT 算法。

3.1.3 求解鲁棒性

为进一步验证算法的鲁棒性，初始仿真数据中增加方差为2 的零均值高斯白噪声，并改变测试点的数目从4～10，采用式（19）分别计算Soft-POSIT、BnB-P2P 算法的旋转矩阵、平移向量误差，结果如图9 所示（SoftPOSIT 算法的初始值在真值的范围内选取）。从图9 中可以看出，存在噪声的情况下SoftPOSIT、BnB-P2P 算法的求解误差要显著大于不存在噪声时的情况（参见图6）。类似于图6 和图7 所得结论，由于本文BnB-P2P 算法由于采用了全局搜索最优值的方法，因此在存在干扰噪声的情况下，求解精度、稳定性要高于SoftPOSIT 算法。

图6 旋转矩阵误差Fig.6 Rotation matrix errors

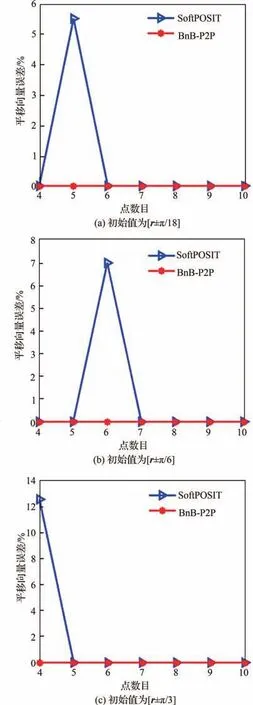
图7 平移向量误差Fig.7 Translation vector errors

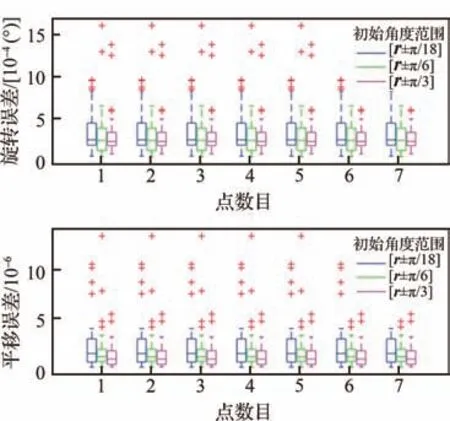
图8 旋转和平移误差箱型图Fig.8 Rotation and translation errors box-plot

图9 噪声情况下的旋转和平移误差Fig.9 Rotation and translation errors in the case of noise

3.1.4 计算效率

对2 种算法设置不同的初始角度范围，并从4～10 改变空间3D 参考点的数目，每个参考点处各算法分别执行100 次，统计各算法的平均运行时间，结果如图10 所示。可以看出，SoftPOSIT由于是局部寻优的算法，因此求解速度快。本文的BnB-P2P 算法需要在整个解的空间上搜索最优值，因此效率低于SoftPOSIT 算法。在明确初始位姿范围且空间参考点数目较少的情况下，本文BnB-P2P 算法和SoftPOSIT 算法所消耗的时间相差不大。但随着初始位姿范围的扩大和空间参考点数目的增加，本文BnB-P2P 算法的寻优时间显著增加，原因在于本文算法的复杂度是O(n2)。综合以上考虑，本文BnB-P2P 算法适用于空间点数目较少且要求位姿求解精度较高的场合（如基于视觉的空间交汇对接、视觉辅助无人机降落等任务）。在不需要考虑运行效率的位姿求解任务中，相比于SoftPOSIT 算法，本文BnB-P2P 算法有更可靠的收敛率、更高的求解精度，具有明显的优势。

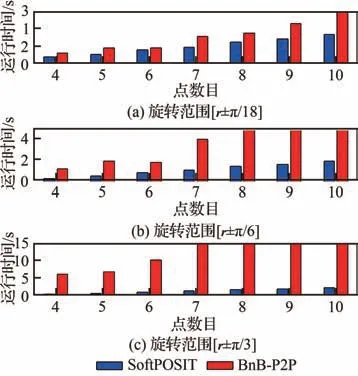
图10 计算效率Fig.10 Computational efficiency

3.2 实物实验

采用现实增强的方式验证对比算法，实验中使用的相机分辨率为1 292×964 像素，像元尺寸为3.75 μm。采用张正友法［28］标定相机内参数，结果如表1 所示。

表1 相机标定结果Table 1 Camera calibration result

以118 mm×118 mm×82 mm 的长方体为模型，对其7 个可以目视的三维顶点提取2D 图像坐标，如图11（a）中绿点所示。三维顶点在3D 空间的真实坐标可以由长方体的尺寸计算得到。长方体顶点的2D 图像坐标和其3D 顶点坐标的对应匹配关系未知，分别采用SoftPOSIT 算法和BnB-P2P 算法求解长方体模型在相机坐标系下的位姿。对于SoftPOSIT 算法，初始值首先选择在真值较近处，通过迭代计算得到长方体在相机下的旋转矩阵和平移向量，并利用该计算值将长方体模型的3D 顶点投影到图像平面，结果如图11（b）所示，可见SoftPOSIT 算法投影模型能够和真实模型较好重合，证明当初始值离真值范围较近时，SoftPOSIT 算法能够有效收敛到真值。然后，将SoftPOSIT 算法的初始值设置为r=[0，0，0 ]，同样使用迭代结果得到投影长方体模型的3D 顶点，如图11（c）所示，可见当初始值离真值范围较远时，SoftPOSIT 算法不能有效收敛于真实值，容易导致位姿求解出现错误。对于本文BnB-P2P 算法，无需选择迭代初始值，直接给定旋转参数的搜索空间为[-π，π]。同样利用最终搜索的位姿参数将长方体模型的3D 顶点投影到图像平面，如图11（d）所示。可以看出，本文BnB-P2P 算法能够在旋转参数的整个定义域空间上搜索并收敛于真实值，迭代求解位姿真值的能力明显好于SoftPOSIT 算法。图12 为BnBP2P 算法搜寻最优旋转参数时上界和下界的收敛曲线，大约经过5 000 次迭代以后，BnB-P2P 算法的上界和下界偏差小于预先设定的精度，最终收敛于最优值。

图11 使用3D 模型的投影增强图像Fig.11 Images augmented by using projections of 3D model

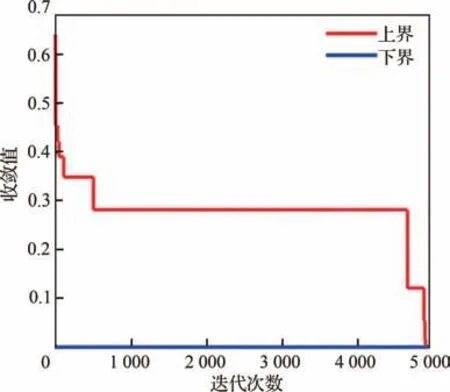
图12 收敛曲线Fig.12 Convergence curves

4 结论

1）本文推导出了一种新的基于点和点约束的SPCD 问题求解模型，该模型中仅含有旋转参数，不含有平移参数，优化求解时无需采用交替迭代的方式。

2）基于推导的新模型，从角度距离出发构建了求解SPCD 问题的优化目标函数，并采用分支定界搜索的方法在旋转参数的全局空间上搜寻最优的相机位姿和最佳的3D/2D 匹配关系。

3）实验表明，相比于传统SoftPOSIT 算法，本文算法的收敛率成功率更高，位姿求解的精度更好，并且求解时无需精确的初始值，可以在旋转参数的整个定义域空间上搜索寻优，具有更好的适应性。