CPT及IRPT多场景电流分解对比及分析

丁 勇，茆美琴

（合肥工业大学光伏系统教育部工程研究中心，安徽合肥 230009）

0 引言

功率理论是分析电路传输功率、计量电费的依据，同时作为电流信号分解方法，也广泛应用于有源滤波器及功率变换器控制中用于生成参考电流［1-2］。传统功率理论在单相及三相对称正弦电压条件下的功率传输现象分析、功率补偿等领域已得到普遍认可。而在三相非正弦电压条件下，传统功率理论不再适用［3］。随着电力电子化电力系统的不断发展，可再生能源渗透比例持续增加，新型负荷应用快速增长，系统中尤其是在容量较小的微电网边界内，不对称／不平衡、非正弦、非线性现象将日益明显。例如随意连接的单相分布式电源（distributed generator，DG）及负荷将造成源侧及荷侧功率不平衡［4］、电力电子接口将引入高频扰动［5］、电动汽车充电可能产生谐波污染［6］等。因此，寻求适用于非正弦条件下的功率理论在当前建设以新能源为主体的新型电力系统背景下有着重要的理论及现实意义。

从20世纪20年代起，关于非正弦电压条件下的各种功率理论学说相继被提出。按照适用系统不同，可分为单相、三相及单／三相非正弦功率理论3类；按照处理域不同，可分为频域功率理论［7-10］、时频域功率理论［11］、几何代数域功率理论［12］及时域功率理论［13-16］4类。其中，频域功率理论和时频域功率理论需要采用傅里叶变换获得电压、电流信号各次谐波表达式，分析通常较为复杂、费时，一般应用于电路稳态分析，特别是谐波分析领域。典型理论包括频域中的Budeanu 理论［7］、S&Z 理论［8］、Sharon 理论［9］、IEEE 1459—2010 标准［10］及时频域中的电流物理分量（currents’physical component，CPC）理论［11］等；几何代数域功率理论［12］通过引入几何代数变换将时域电压、电流信号映射到几何代数域中，定义电压和电流向量的几何积为电路的几何视在功率，其包含电路的瞬时有功及无功功率信息。几何代数域功率理论涉及几何代数域及时域间的多次变换，且目前仅适用于单相非正弦系统。相比而言，时域功率理论直接对电压、电流信号进行时域计算，不涉及傅里叶变换及几何代数映射，具有“瞬时性”或“类瞬时性”特征，可更好地适应电力电子设备的实时控制要求，典型时域功率理论包括Fryze 理论［13］、FBD 理论［14］、瞬时无功功率理论（instantaneous reactive power theory，IRPT）［15］、守恒功率理论（conservative power theory，CPT）［16］等。

上述功率理论已分别在非正弦系统电路分析、计量、功率补偿、功率控制等领域得到应用，但应用于相同电路时可能得到彼此不同甚至相互矛盾的结果，其主要原因在于各理论采用的电流／功率分解方式不一。换言之，上述功率理论只适用于特定的应用领域。例如IRPT 已被广泛应用于对称正弦三相系统的有源滤波领域，但不能用于电费计量，且不适用于单相系统。CPT 作为一种新兴的时域功率理论，近年来越来越受到关注，被认为是可能同时应用于电路分析、计量、补偿及功率变换器控制的“通用”功率理论［17］。

不同功率理论间的比较已有少量研究，但多为理论及数学阐述［18-19］。也有部分文献进行了IRPT或CPT 与其他功率理论的对比研究，但总体上通过具体案例对IRPT 与CPT 在电流分解中的应用进行对比，还鲜有成果报道。为此，本文在介绍基于IRPT 及CPT 的电流分解原理基础上，构建含不同源荷特性的多类型三相电气系统场景，通过具体应用场景对比，直观分析2 种时域功率理论间的联系与不同，为2 种功率理论应用于不同场景下计量、滤波、功率变换等装置中的设计与控制提供参考。

1 IRPT及CPT理论基础

IRPT 及CPT 均属于时域功率理论，2 种功率理论对电流、功率的定义均在时域中进行，直接对电压、电流信号进行时域计算。其中，IRPT 在α β坐标系下对各电流、功率项进行定义，CPT 的电流、功率项定义则是在abc坐标系下完成。

1.1 IRPT理论基础

IRPT 主要依据Clarke 变换将abc坐标系中的三相系统电压及电流信号xn（x=v，i分别表示电压、电流信号；n=1，2，3，分别表示A、B、C 相）转换成α β坐标系中的电压、电流信号xα、xβ，进而在α β坐标系下定义系统的瞬时有功功率、瞬时无功功率及相关的电流项。abc坐标系与αβ坐标系之间的关系如附录A 图A1 所示。由图A1 及式（1）可将x1—x3变换为xα、xβ，如式（1）所示。

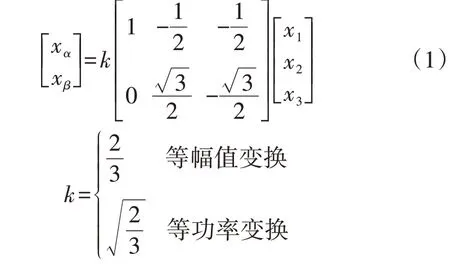
IRPT框架下的瞬时复功率S与传统功率理论中的复功率类似，定义为α β坐标系下的电压矢量v与电流矢量i的共轭复数i*的乘积，即：

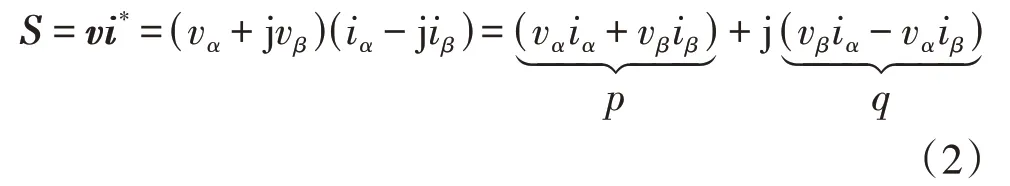
式中：p为瞬时有功功率或瞬时实功率；q为瞬时无功功率或瞬时虚功率；vα、vβ分别为v的α、β轴分量；iα、iβ分别为i的α、β轴分量。

根据式（2），可得αβ坐标系下瞬时电流iα、iβ为：

基于IRPT 的电流分解示意图如图1 所示。在存在畸变的情况下，瞬时有功、无功功率均包含两部分，即直流（平均）分量pˉ及qˉ、交流（振荡）分量p͂及q͂。q对负载与电源之间的能量流在任意瞬间都没有贡献，表示系统各相之间交换的能量大小，其决定了瞬时无功功率α、β轴分量的大小，瞬时无功功率α、β轴分量之和总等于0。pˉ及qˉ仅与基波电压、电流有关，而p͂及q͂与谐波／不平衡电压、电流有关。

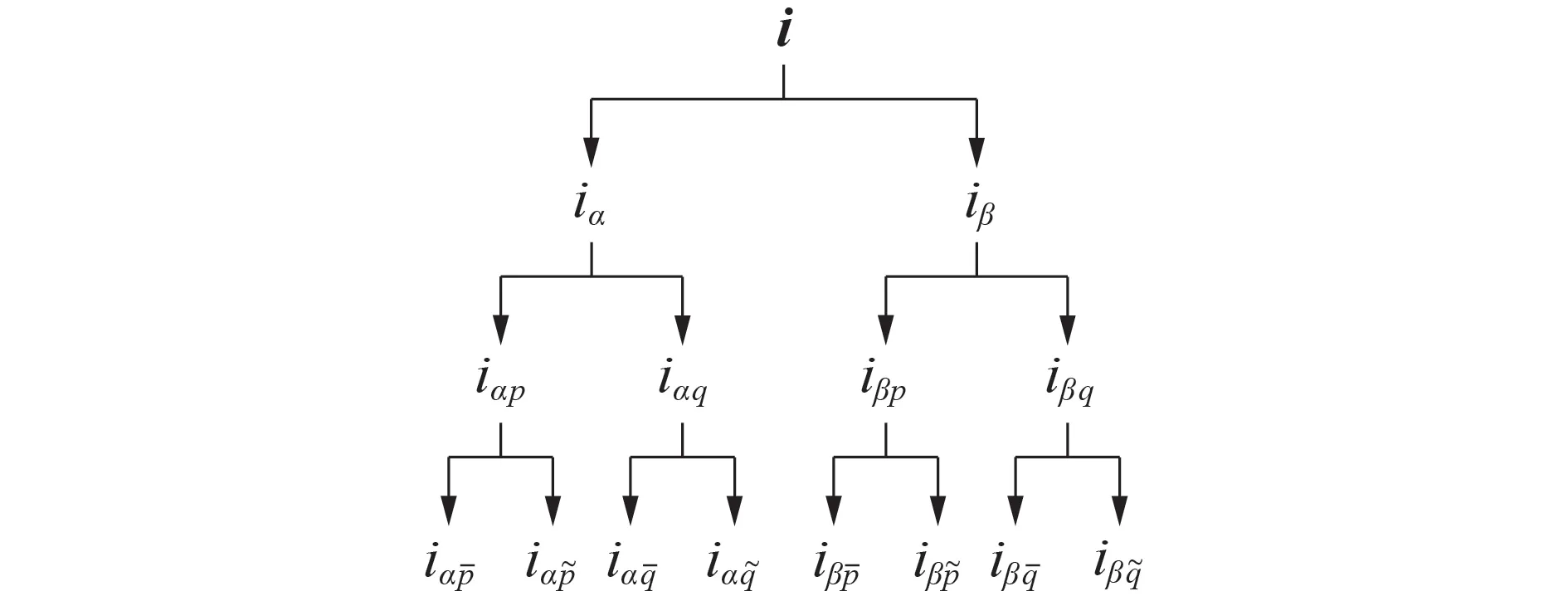
图1 基于IRPT的电流分解示意图Fig.1 Schematic diagram of current decomposition based on IRPT

通过上述分解，系统三相电流在IRPT 框架下可用αβ坐标系下的8 项子电流表示，对应的α、β轴子电流经过Clarke 反变换即可得到abc坐标系下的各子电流，其中平均有功、无功电流与基波分量有关，瞬时有功、无功振荡电流与谐波、不平衡分量有关。

1.2 CPT理论基础

CPT 主要根据电压及电流的“无偏变量”或“同源变量”，定义相关的功率项及电流项，“无偏变量”或“同源变量”的定义［16］为：

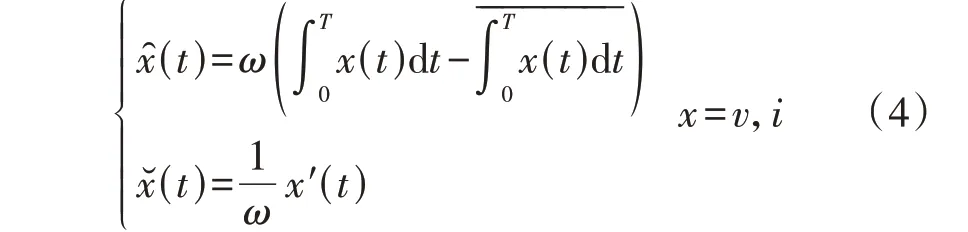
式中：ω为信号频率；T为周期；“—”表示平均值计算；x′(t)为x(t)的微分；“^”为同源积分标志；“˘”为同源微分标志。

依据上述电压、电流的“无偏变量”及原始变量，可以获得多种守恒的功率或功率相关的定义［17］。CPT 最常采用的瞬时有功功率p及无功能量w定义为：

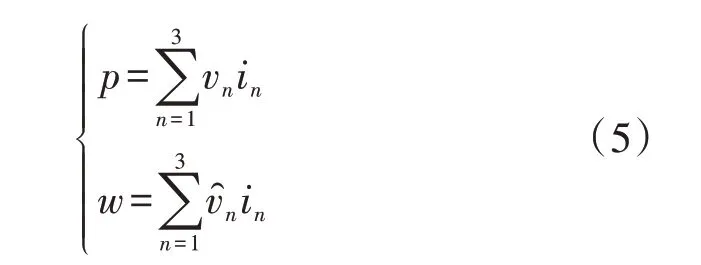
在单相系统中，CPT相关电流定义为：

式中：“＜·，·＞”表示内积计算，具体运算见附录B 的B1 部分；P、W分别为系统平均有功功率、无功能量；V和V̑分别为电压有效值及其同源积分变量的有效值；Gact为等效电导；Brea为等效无功性；iact为有功电流，irea为无功电流，ivoid为空电流，根据定义可知，这3项电流彼此正交，且具有明确的物理意义，与特定的功率现象相关［16］。

在三相系统中，各相有功、无功电流定义与单相系统定义一致，但因三相系统可能存在负荷不平衡，CPT 将各相有功及无功电流进一步分解成平衡有功电流和不平衡有功电流，分别如式（7）、（8）所示。

从式（7）、（8）可看出，CPT 下定义的各相平衡有功电流及无功电流始终分别与各相电压及电压同源积分波形呈比例关系。

综上所述，三相系统电流在CPT 下可分解为平衡有功电流、平衡无功电流、不平衡有功电流、不平衡无功电流及空电流，且各项电流彼此正交，具体分解如图2所示。

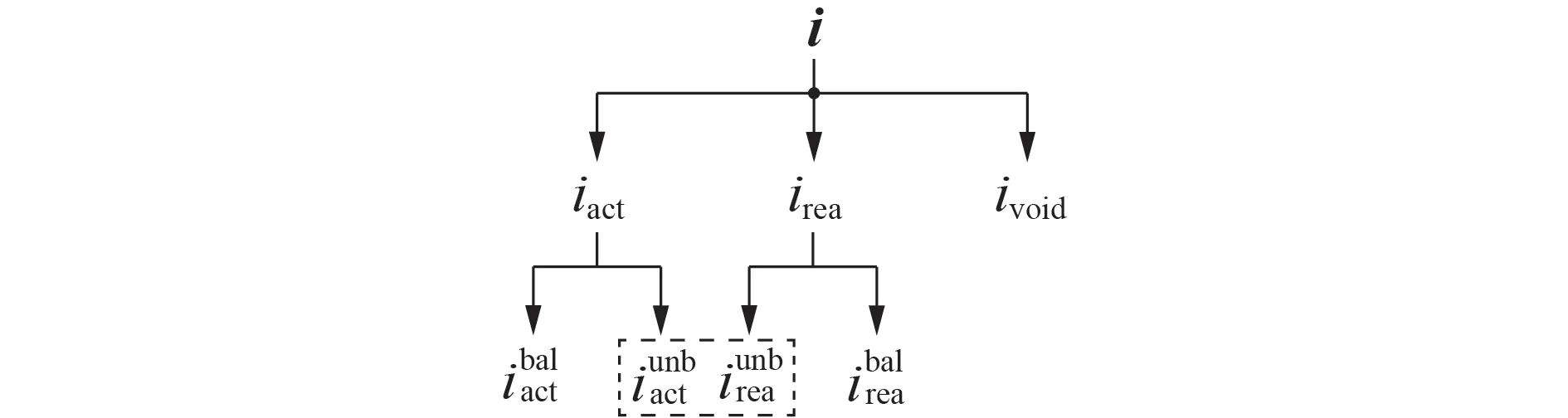
图2 基于CPT的电流分解示意图Fig.2 Schematic diagram of current decomposition based on CPT

相较于IRPT 而言，CPT 可将电流分解为更多与特定物理现象如无功损耗、谐波等相关联的子项，尤其是可提取出系统中的不平衡电流。更多电流信息的获取，为灵活电流补偿及逆变器控制提供了理论基础。值得说明的是，在正弦线性条件下，CPT 的功率定义与传统功率理论定义具有一致性，传统功率理论中的功率定义可视为CPT 功率理论的特例，详细说明见附录B的B2部分。

2 基于IRPT及CPT的电流检测与分解

对原始电流进行合理、准确的分解，是后续电流补偿及控制的关键。本节基于第1 节所述的IRPT及CPT 的基本理论基础，阐述基于IRPT 及CPT 的电流检测及分解方法。

2.1 基于IRPT的电流分解方法

2.2 基于CPT的电流分解方法

根据式（4）—（8）可得到基于CPT的电流检测与分解方法，如图4 所示。图中：RMS 表示有效值计算；AVE表示平均值计算，用于计算各相的无功能量Wn及有功功率Pn，进而根据式（6）和式（7）分别计算各相有功电流iactn、无功电流irean和各相平衡有功电流ibalactn、平衡无功电流ibalrean；各相电流与各相有功、无功电流之差即为各相空电流ivoidn；各相有功电流与平衡有功电流之差、无功电流与平衡无功电流之差分别为不平衡有功电流iunbactn、不平衡无功电流iunbrean。

图3 基于IRPT计算p、q的电流检测示意图Fig.3 Schematic diagram of IRPT-based current detection using p and q calculation

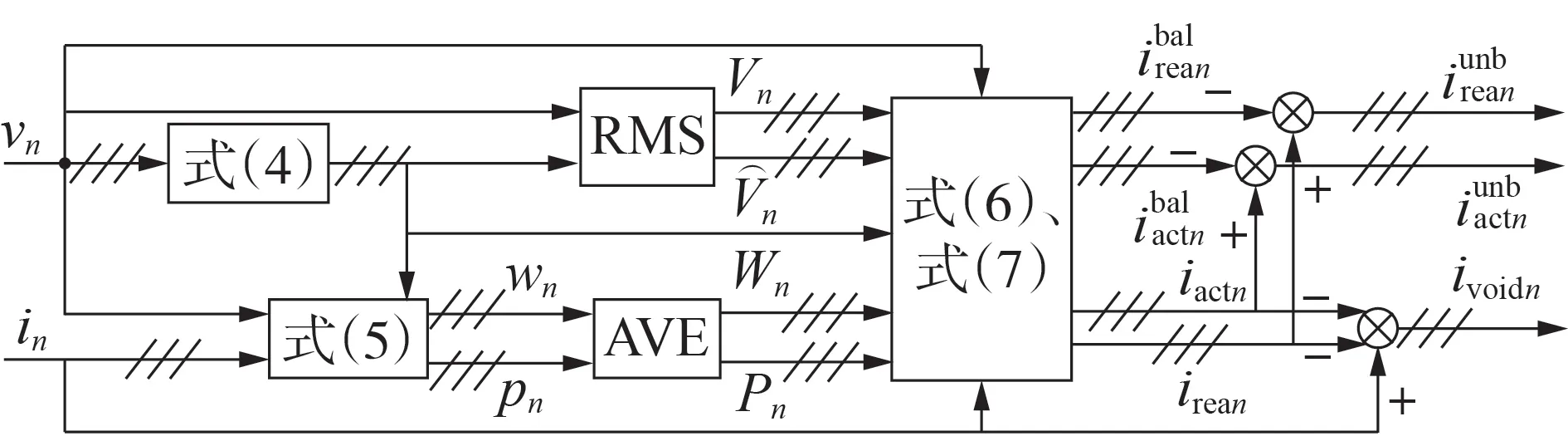
图4 基于CPT的电流检测示意图Fig.4 Schematic diagram of CPT-based current detection

3 多场景应用对比与讨论

为了评估基于IRPT 及CPT 在不同条件下的电流检测与分解效果，本文在MATLAB／Simulink 环境下构建含不同源荷特性的多类型三相系统运行场景，并对各场景下的电流分析结果进行比较。需要说明的是，本文各场景中，电源中性点引出接地，以此为参考电压，使用3 个电压测量模块采集各相电压。在电压中性点未引出的情况下，可采用虚拟星接法获取各相电压［20］。

3.1 场景1：含正弦电压、不平衡负荷

本场景的系统结构及源荷参数分别如图5及表1所示，图5中vM、iM分别为电压测量点、电流测量点。

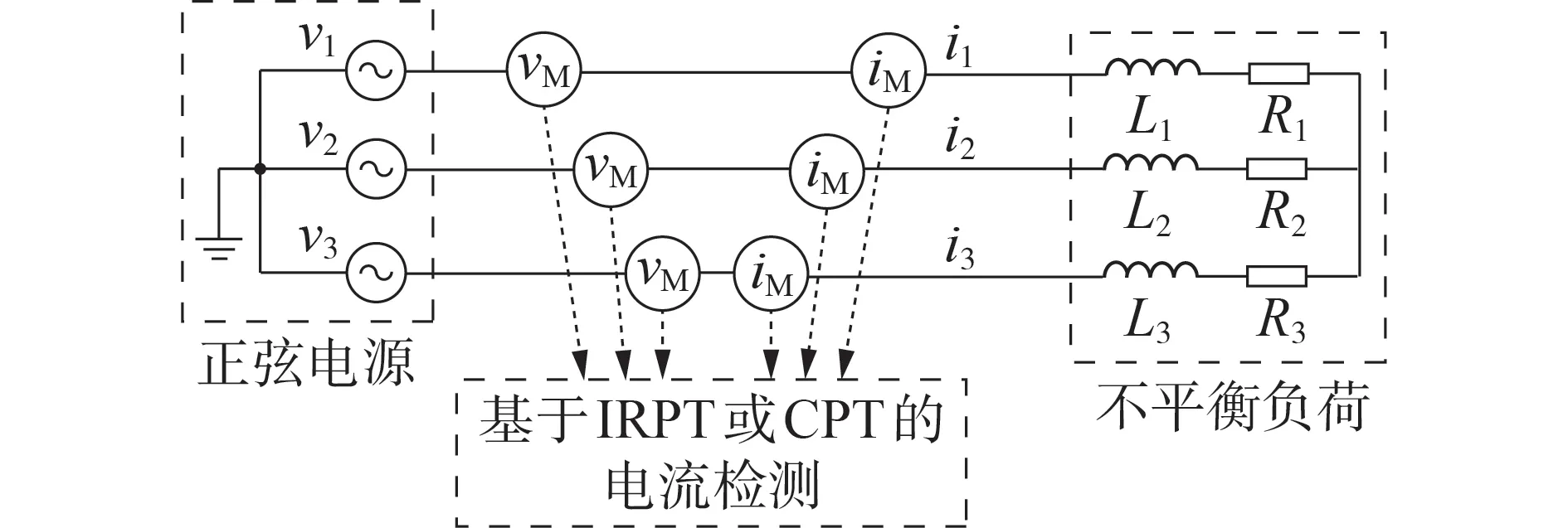
图5 场景1下系统结构Fig.5 System structure in Scenario 1

表1 场景1下系统参数Table 1 System parameters in Scenario 1

系统三相电压、电流波形如附录C 图C1 所示。由图可见：三相系统电压为正弦对称电压；但因不平衡负荷的存在，三相电流呈现不平衡状态，且因存在感性负荷，各相电压超前电流一定相位。

基于IRPT 的电流分解结果见图6。图中，A 相电压分别等比例压缩为原波形的1/20及1/200，后续各场景均如此处理，不再赘述。由图可见：基于IRPT得到的平均有功电流与电压同相位，反映了负荷中的阻性分量；类似地，IRPT 平均无功电流滞后电压90°，反映了负荷中的感性分量。本场景中，振荡电流不为0，说明系统负荷存在不平衡或／和非线性特性，但不能进一步分析究竟由何种非理想特性引发。

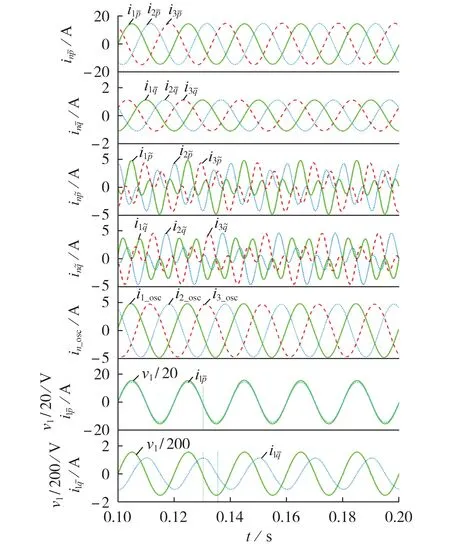
图6 场景1下基于IRPT的电流分解结果Fig.6 Current decomposition results based on IRPT in Scenario 1

基于CPT 的电流分解结果见图7。图中：inonan为各相非有功电流；A 相电压及其同源积分等比例缩小为原波形的1/40，平衡有功电流缩小为原波形的1/4，后续各场景均如此处理，不再赘述。由图可见：基于CPT 得到的各相平衡有功电流与电压、平衡无功电流与电压同源积分（滞后原始电压90°）波形分别同相位且成比例，这表明基于CPT 得到的平衡有功及无功电流分别反映了负荷中平衡线性阻性和感性负荷分量；CPT 可进一步将负荷不平衡及非线性特性分离，其中不平衡有功及无功电流反映了各相负荷阻性及无功性（本文为感性）分量同等效平衡阻性及无功性分量之间的差异；因本场景不含非线性负荷且电压未畸变，因此反映非线性特性的空电流为0；非有功电流反映了除平衡阻性负荷之外其他所有非理想负荷特性，本场景中其反映了负荷不平衡及无功性。

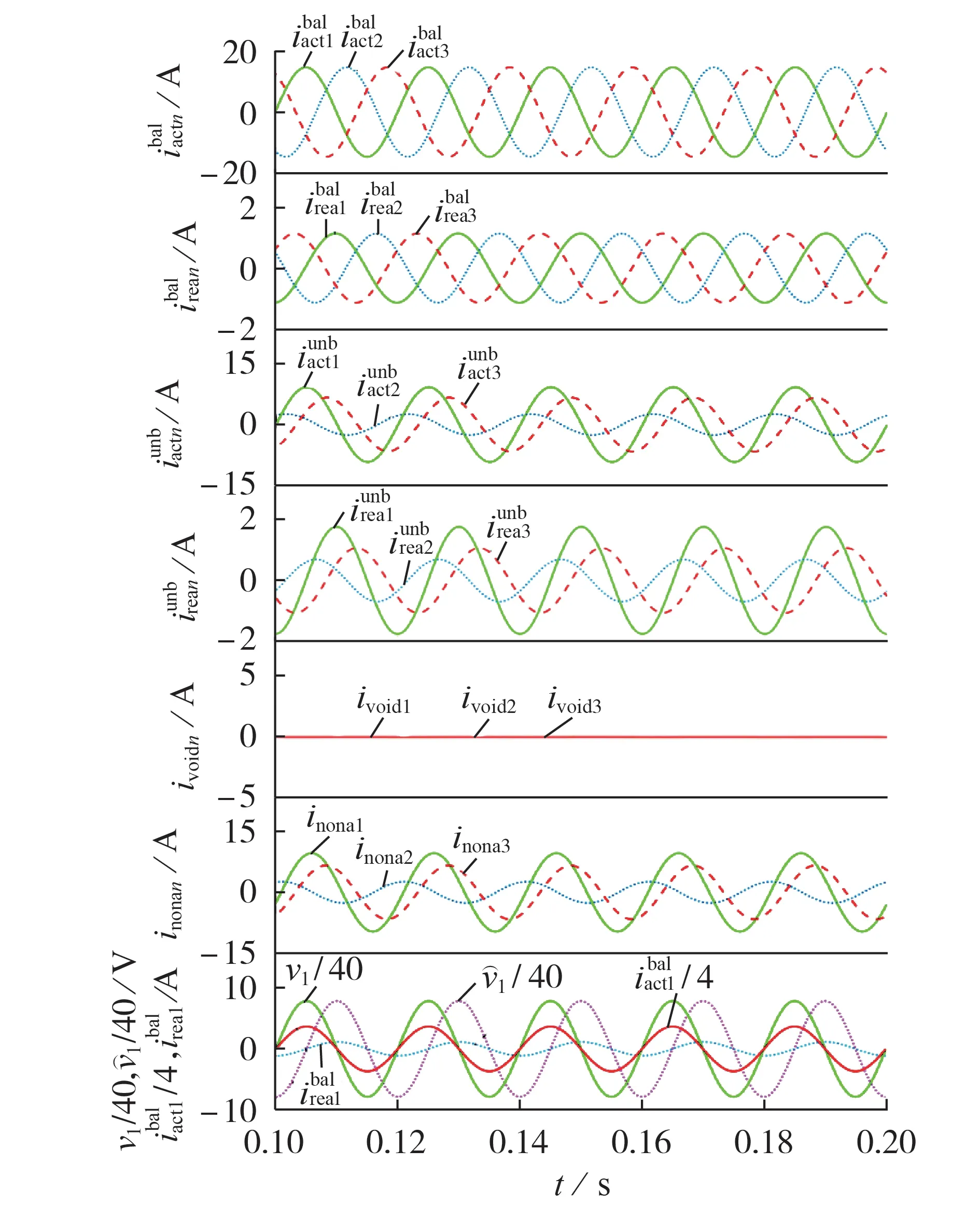
图7 场景1下基于CPT的电流分解结果Fig.7 Current decomposition results based on CPT in Scenario 1

进一步观察可以发现，平衡有功及无功电流、不平衡有功及无功电流、空电流两两正交，限于篇幅，仅展示平衡有功电流与平衡无功电流、不平衡无功电流与空电流间的内积，如附录C图C2所示。

若将本场景中负荷改为平衡负荷R1=R2=R3=13 Ω，L1=L2=L3=5mH，则不平衡有功／无功电流将均为0，如图8所示，这表明负荷中无不平衡现象。进一步地，若将本场景下的负荷替换为仅含不控整流的非线性负荷，则基于CPT 得到的不平衡有功、无功电流将仍然为0，其他相关电流分解结果如图9 所示。由图可见，基于IRPT 得到的振荡电流与基于CPT 得到的空电流波形相同，而基于IRPT 得到的振荡有功、无功电流不为0。这进一步说明：采用CPT 时，负荷不平衡与非线性特性可分别由不平衡电流及空电流体现；而采用IRPT 时，振荡电流反映的是不平衡及非线性综合效应，不可进一步分解。

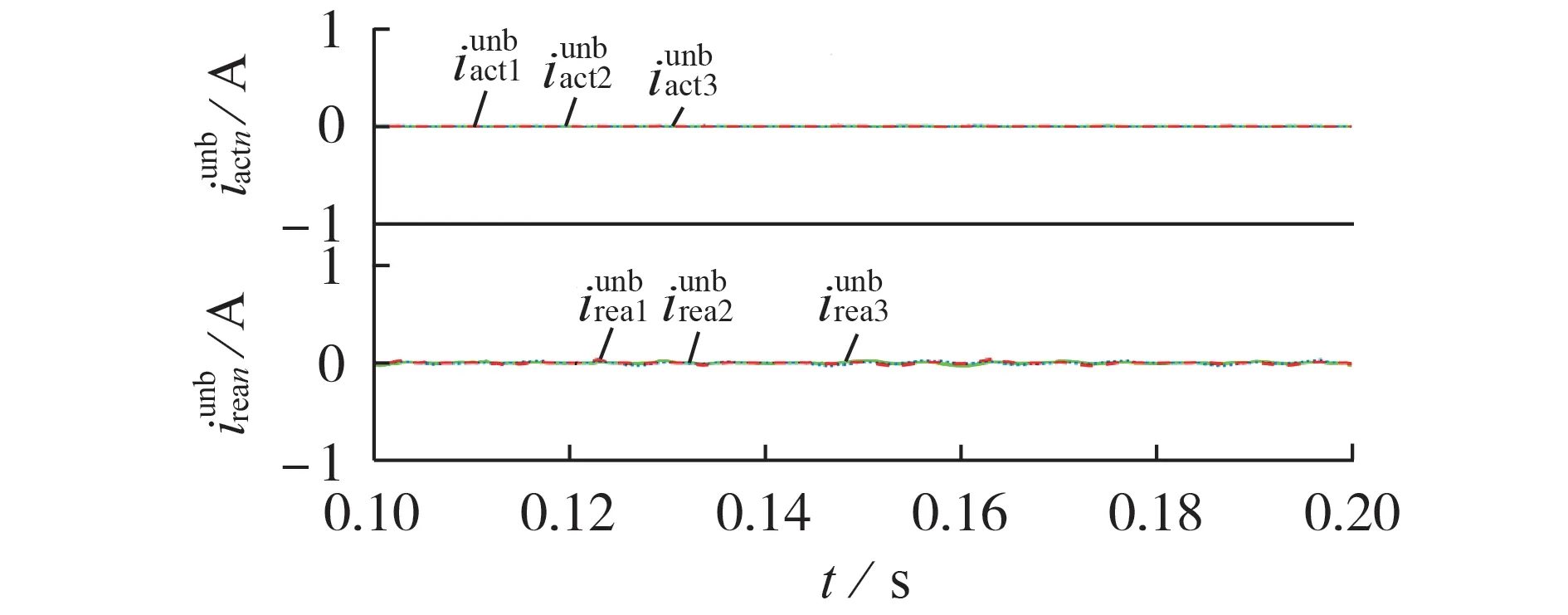
图8 仅含平衡负荷时基于CPT得到的不平衡有功、无功电流Fig.8 Unbalanced active and reactive currents obtained by CPT when balanced loads are connected

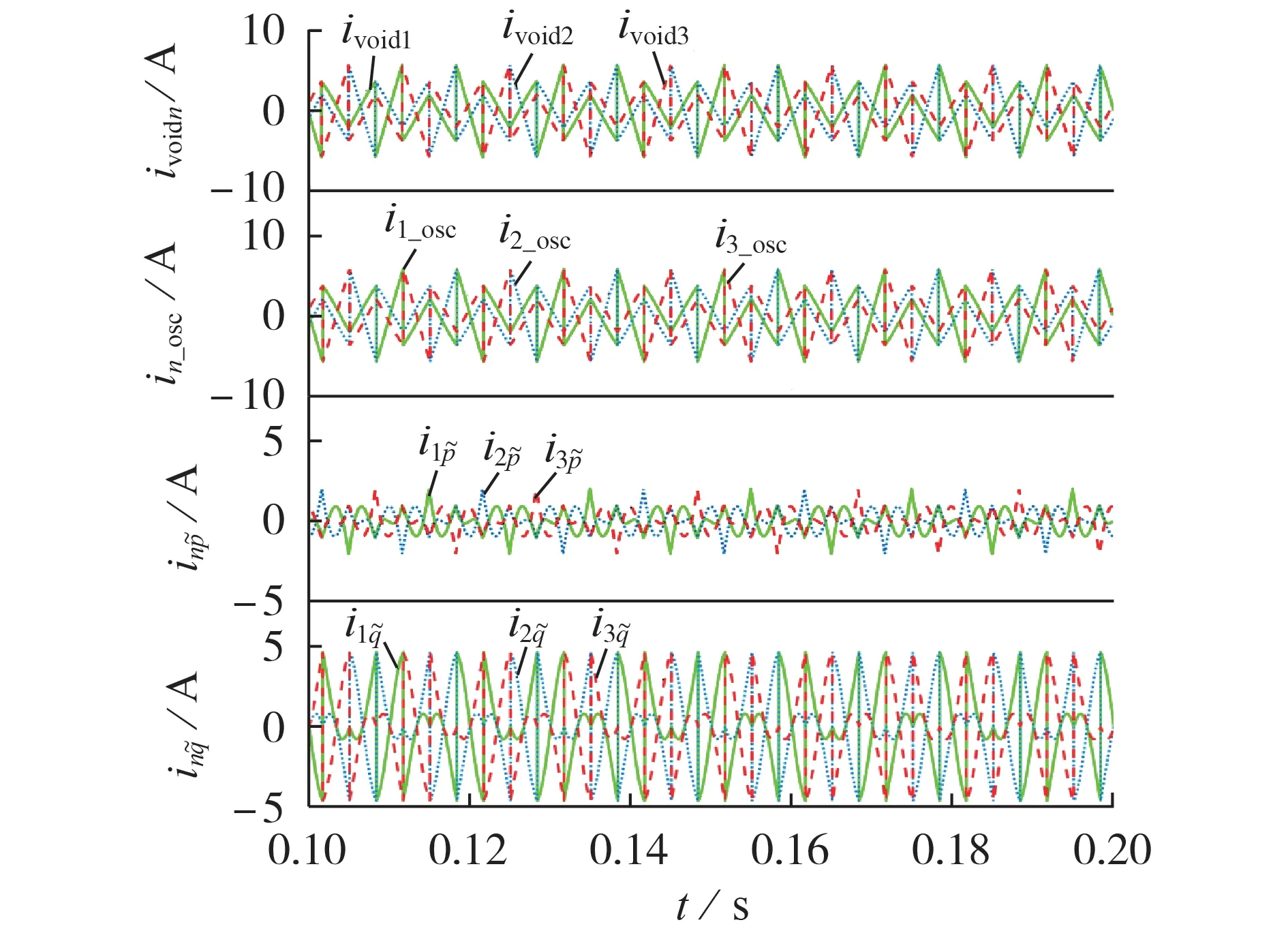
图9 仅含非线性负荷时的相关电流Fig.9 Related currents when only non-linear loads are connected

另外，根据图6、7 可观察到本场景中基于IRPT得到的平均有功电流与基于CPT得到的平衡有功电流相等，将式（3）、（7）中两电流表达式重写为：

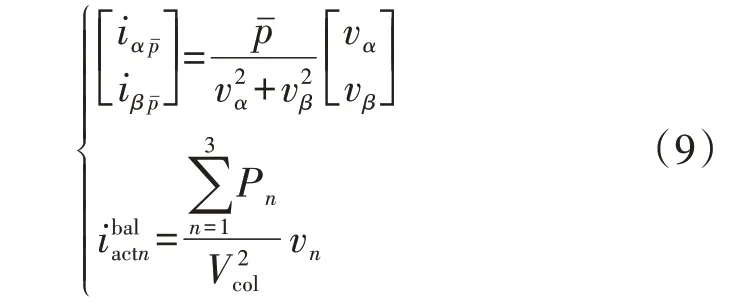
本场景下电压为三相正弦电压，故基于IRPT 得到的平均有功电流α、β轴分量中的电压相关项在变换到abc坐标系后，与基于CPT得到的平均有功电流中的电压相关项相同，且二者中的有功功率项也相等，因此IRPT 平均有功电流与CPT 平衡有功电流在本场景中是一致的。

由式（9）还可以观察到：IRPT 下的平均有功电流计算涉及瞬时有功功率平均分量获取，应用中一般通过低通滤波器实现，这意味着基于IRPT 得到的平均有功电流准确度与低通滤波器的性能有着密切关系；而基于CPT 得到的平衡有功电流计算涉及的有功功率一般通过平均值模块获取，其始终为常数，且式（9）中涉及的电压有效值也为常数，故基于CPT得到的平衡有功电流能够始终跟踪电压波形，仿真结果与理论分析一致。

尽管IRPT 及CPT 分解得到的各电流子项有所差异，但其各相子电流之和iIRPTn及iCPTn均可还原原电流，如图10所示。

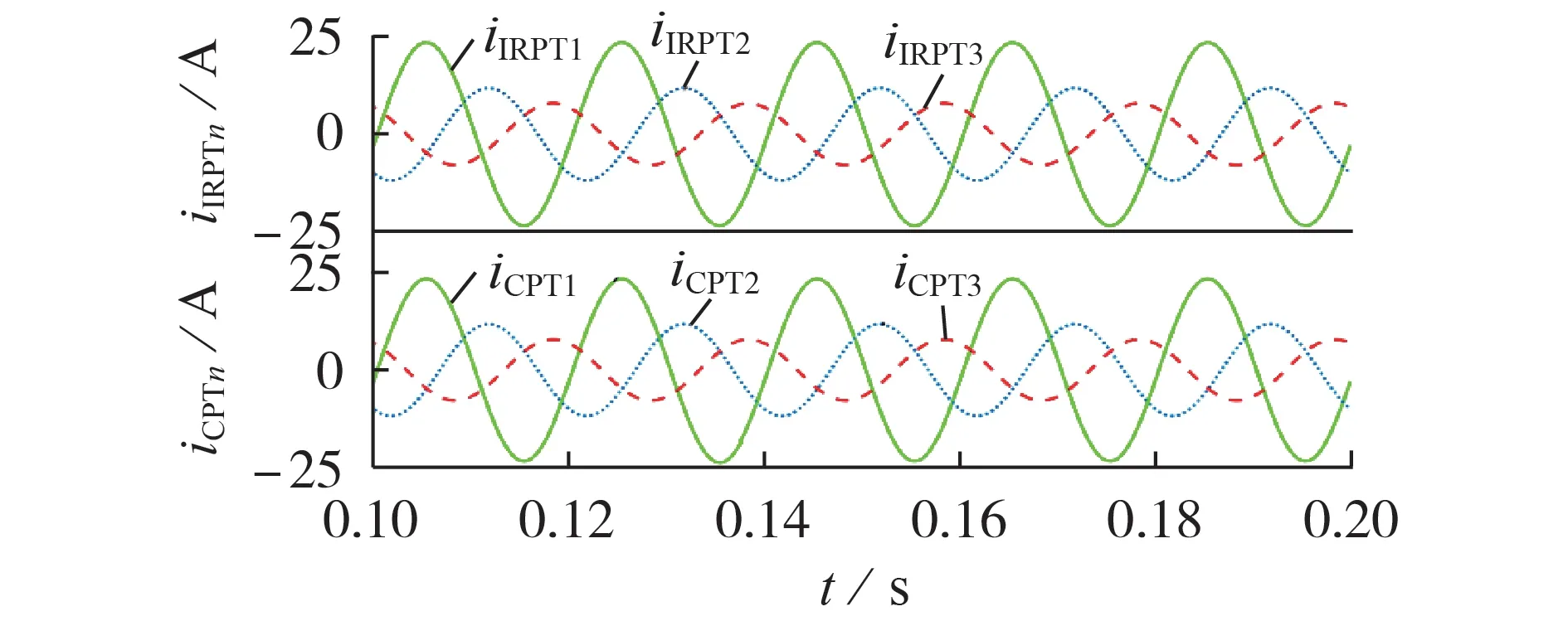
图10 场景1下基于IRPT、CPT得到的各相分解电流之和Fig.10 Sums of decomposed currents of each phase obtained by IRPT and CPT in Scenario 1

3.2 场景2：含正弦电压、不平衡及非线性负荷

本场景中，系统电压为标准三相对称正弦电压，负荷含三相不平衡负荷及非线性负荷，系统结构如附录C图C3所示，源荷参数如附录C表C1所示。

本场景下的系统三相电压、电流如附录C 图C4所示。由图可见，本场景下三相系统电压为正弦电压，但因不平衡、非线性负荷存在，三相电流发生畸变、不平衡。且因存在感性负荷，各相电压均超前电流一定相位。

本场景下基于IRPT、CPT 的电流分解结果分别如附录C 图C5、C6 所示。由图C5 可见：本场景下，基于IRPT 得到的平均有功电流、平均无功电流分别与电压同相位、滞后电压90°，分别反映了负荷中的阻性分量和感性分量；本场景中振荡电流也不为0，同样说明负荷存在不对称或／和非线性分量，但IRPT无法进一步分解。而由图C6可见：基于CPT得到的各相平衡有功电流与电压、平衡无功电流与电压同源积分波形分别同相位且成比例，表明CPT 平衡有功及无功电流分别反映了负荷中的平衡线性阻性和感性负荷分量。与IRPT 不同，CPT 可进一步将负荷不平衡及非线性特性分离。本场景下的负荷包含非线性负荷，因此空电流不为0；非有功电流在本场景下反映了负荷不平衡、无功性及非线性。此外，本场景下基于CPT 得到的各分解电流也两两正交，部分结果如附录C 图C7 所示。本场景下基于IRPT及CPT 分解得到的各电流子项之和均可还原原电流，如附录C图C8所示。

3.3 场景3：含非正弦电压、不平衡负荷

本节构建含非正弦电压、不平衡负荷场景，系统结构与源荷参数分别如附录C图C9与表C2所示。

本场景下的系统三相电压均含有10%的5次谐波，且B、C 两相电压的基波幅值分别为A 相电压基波幅值的80%、90%，如附录C 图C10 所示。尽管负荷不含非线性负荷，但由于电压的畸变，三相电流也发生畸变、不平衡。且因负荷中存在感性负荷，各相电压超前电流一定相位。

本场景下基于IRPT、CPT 得到的电流分解结果分别如附录C图C11、C12所示。

由图C11 可见，场景3 中基于IRPT 得到的平均有功电流与电压同相位，负责从“源”向“荷”单向传送功率。但是二者波形不同，主要原因在于利用式（3）计算α、β轴平均有功电流分量时，计算系数vαβ/(v2α+v2β)由于电压畸变且不对称而存在波动，导致平均有功电流也畸变不对称，如附录C 图C13 所示。观察本场景下的平均无功电流可发现其滞后电压90°。本场景下，振荡电流不为0，说明负荷存在不对称或／和非线性分量，但IRPT无法进一步分解。

由图C12 可见，本场景下基于CPT 得到的各相平衡有功电流与电压、平衡无功电流与电压同源积分的波形分别同相位且成比例。换言之，平衡无功电流滞后电压90°相位。因此，基于CPT得到的平衡有功及无功电流分别反映了负荷中的平衡线性阻性和感性分量。从式（7）可以发现，不管系统电压波形如何，因基于CPT 计算有功电流、无功电流时仅涉及有效值，故可分别跟踪电压及电压的同源积分。CPT 可进一步将负荷不平衡及非线性特性分离，其中，不平衡有功及无功电流分别反映了负荷各相阻性及感性分量与等效平衡阻性及感性分量之间的差异。本场景虽然不含非线性负荷，但由于畸变电压导致负荷电流也产生了畸变，因此本场景下空电流不为0。本场景下基于CPT 得到的各分解电流也两两正交，部分结果如附录C图C14所示。

事实上，若对本场景系统电压及负荷电流采用快速傅里叶变换分析，则可以发现本场景下负荷电流与电压一样也仅含有5 次谐波。在CPT 早期定义中，将空电流还分解为杂散有功电流isa、杂散无功电流isr及负荷生成电流ig，三者相互正交［20］。其中杂散有功／无功电流反映不同谐波次数下各等效电导／无功性之间的差异，负荷生成电流反映仅由负荷而非电压引起的电流谐波畸变。在本场景下，负荷生成电流ig=0，表示电流谐波畸变仅与非正弦电压相关。随着CPT 在功率补偿及控制领域应用的不断发展，借助于频域分析对空电流进一步分解的必要性逐渐降低。近年来的相关研究基本不再对空电流进行分解，仅在利用CPT详细分析电路现象、源荷谐波责任划分等少数应用场合使用。

本场景下基于IRPT 及CPT 分解得到的各子电流之和也均可还原原电流，如附录C图C15所示。

3.4 场景4：含非正弦电压、不平衡及非线性负荷

本节构建了含非正弦畸变电压、不平衡及非线性负荷场景，该场景可能在未来尤其是微电网边界内高比例可再生能源及电力电子设备渗透背景下普遍存在，系统结构与参数分别如附录C 图C16 与表C3所示。

本场景下的系统电压、电流波形如附录C 图C17所示。由图可见，本场景下的电压波形与场景3下一致，三相电流因电压非正弦及不平衡、负荷非线性而发生畸变与不平衡，且因负荷中存在感性负荷，各相电压均超前电流一定相位。

本场景下基于IRPT 及CPT 的电流分解结果分别如附录C 图C18、C19 所示。由图C18 可见，场景4中基于IRPT 得到的平均有功电流与电压同相位，负责从“源”向“荷”单向传送功率，但是二者波形不同，原因与场景3 相同，即均是由电压非正弦畸变所致。本场景中，振荡电流不为0，说明负荷存在不对称或／和非线性分量，但IRPT 无法进一步将不对称及非线性分量进行分解。由图C19 可见，CPT 各相平衡有功电流与电压、平衡无功电流与电压同源积分波形分别同相位且成比例。平衡有功及无功电流分别反映了负荷中的平衡线性阻性和感性分量。CPT 可进一步将负荷不平衡及非线性特性分离，其中不平衡有功及无功电流分别反映负荷各相阻性及感性分量同等效平衡阻性及无功性之间的差异。因本场景负荷包含非线性负荷，且电压存在畸变，因此空电流不为0。且若将空电流进一步分解可发现与场景3中负荷生成电流为0情况不同，本场景中负荷生成电流不为0，表明负荷对电流畸变也有贡献。本场景中非有功电流反映了负荷不平衡、无功性及非线性。本场景下CPT 各分解电流也两两正交，部分结果如附录C图C20所示。本场景下IRPT 及CPT各相子电流之和也均可还原原电流，如附录C 图C21所示。

4 结论

本文通过构建4 种典型场景，对基于IRPT 及CPT 非正弦电压或／和不平衡、非线性负荷条件下的电路分析结果进行综合比较，分析二者联系与不同，为2 种功率理论应用领域与场景选择提供参考依据，所得结论如下。

1）正弦电压条件（场景1、2）下，不管负荷如何，基于IRPT 得到的平均有功／无功电流及CPT 平衡有功／无功电流结果均相同，平均／平衡有功电流与电压同相位且波形成比例，平均／平衡无功电流滞后电压90°，分别反映系统平衡线性（基波）阻性和无功性（本文中为感性）分量。

2）而在非正弦电压条件（场景3、4）下，因电压非正弦畸变，导致基于IRPT 得到的平均有功电流也出现畸变，与电压波形不再一致，且平均有功／无功电流结果同采用的低通滤波器性能关系密切。CPT平衡有功／无功电流计算涉及平均值和有效值，不管电压波形如何，计算系数均为常数，故平衡有功电流始终跟踪电压波形，平衡无功电流始终跟踪电压同源积分。

3）IRPT 振荡电流反映了负荷不平衡与非线性综合效应，在负荷存在不平衡或／和非线性时，振荡电流均不为0，IRPT 不可进一步将二者影响分离（场景1—4）；CPT 可分离负荷不平衡与非线性特性，分别由不平衡电流及空电流体现。

4）在非正弦电压带线性（场景3）及非线性（场景4）负荷情形下，基于CPT 得到的负荷空电流不等于0。可进一步将空电流分解为杂散有功电流、杂散无功电流及负荷生成电流。场景3 中负荷生成电流为0，反映负荷电流谐波畸变仅与电压相关；而场景4中负荷生成电流不为0，反映负荷电流谐波畸变不仅与电压相关，也同负荷相关。

综上所述，CPT 较IRPT 而言具有更广的应用场景，在非正弦、不平衡／非线性场景下均能很好地将负荷电流提取、分解成与负荷特性相关的电流，且各电流彼此正交，可灵活选取电流组合用于功率补偿与功率控制中的参考电流生成；而传统IRPT 仅在正弦电压条件下可有效提取负荷平均有功／无功电流，且无法将不平衡与非线性特性从其振荡电流中提取出来。通过详细对比研究可以发现，与IRPT 相比，CPT 能全面地分解负荷电流以解释电路有功传输、无功消耗、谐波污染、负荷不平衡等物理现象。作为一种新型时域功率理论，CPT 在未来电力系统转型升级中的负荷特征识别、电费计量、滤波补偿、功率变换器控制等领域有着广阔应用前景。

附录见本刊网络版（http：//www.epae.cn）。