光纤阵列准直器设计及其发散角测量
刘若仙, 赵士元, 谷一英, 谢日凡, 赵明山
(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.大连理工大学 光电工程与仪器科学学院,辽宁 大连 116024;3.辽宁省先进光电子技术重点实验室,辽宁 大连 116024)
1 引 言
光纤阵列准直器是光纤通信系统的关键基础部件。随着新一代信息系统向阵列化、宽带化、小型化方向发展,基于微波光子技术的通信雷达等光电子系统对光纤阵列准直器的需求迅速增长,对其性能也提出了更高的要求。光纤阵列准直器急需向低成本、阵列化、集成化方向发展。现有工艺多采用固定折射率透镜(Conventional Lens, C-Lens)和渐变式折射率透镜(Gradient-index Lens, G-Lens)制备光纤阵列准直器,将多个单透镜依次与光纤阵列各通道光纤进行调试、匹配及封装,不断扩展成所需通道数的光纤阵列准直器[1]。武汉光迅通过将多个C-Lens与光纤阵列进行耦合封装,制备出一维多通道光纤阵列准直器[2]。该阵列准直器具有良好的准直特性和较大的工作距离,但阵元间距为3.9 mm,难以满足集成化更高的应用需求,且通道扩展过程中难以保证精确的阵元间距。Zabou等提出直接将透镜集成在光纤端面来制备准直器的方法,可以突破透镜尺寸及光学封装对结构紧凑性的限制[3]。该方法制备的光纤阵列准直器阵元间距在微米量级,但其工作距离有限,多应用在直接跟硅光芯片耦合的应用场合。此外,该方法设计及制造工艺复杂、价格昂贵,准直一致性差。向金山等提出利用衍射型菲涅尔透镜阵列制备光纤阵列准直器的方法[4],通过微光学和微细加工技术制备菲涅尔透镜阵列,设计实现了高密度集成化的光纤阵列准直器,其阵元间距在微米量级。但菲涅尔透镜阵列浮雕结构依靠精确的光学设计,制备工艺复杂,难以保证通道间准直特性的一致性。此外,用以制备的光纤阵列准直器在不同工作波长条件下表现出不同的耦合损耗。近年来,人们采用单点金刚石车削与紫外固化压印技术[5]、光刻胶热熔法[6]等工艺制备微透镜阵列,制备工艺相对简单。所制备的微透镜阵列具有阵元填充率高、阵元位置精确、面形均匀度好等优点,且在一定的工作波长范围内耦合效率一致性好[7],还可根据实际应用需求扩展成多维任意布局的光纤阵列准直器。采用微透镜阵列来制备光纤阵列准直器,阵元间距可以达到光纤自身纤芯直径这一极限值。本文基于该思路,将平凸微透镜阵列用于设计与制备光纤阵列准直器,通过对光纤阵列准直器的准直特性进行理论分析和仿真,确定光纤阵列准直器的相关设计参数,加工制备光纤阵列准直器。最后,通过远场光斑法对光纤阵列准直器的主要性能参数远场发散角进行测量,并采用蒙特卡洛法对测量不确定度进行分析与评定。
2 理论分析与参数设计
2.1 高斯光束变换理论
高斯光束在自由空间中的传播如图1所示。
基模高斯光束在横截面内的场振幅分布按照高斯函数从中心向外平滑降落,由振幅降落到中心值的点所定义的光斑半径ω(z)为[8]:
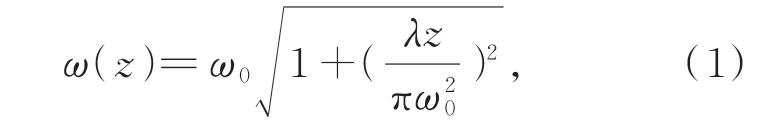
式中:ω0为高斯光束的束腰半径;z为以束腰为坐标原点的轴向距离;λ为工作波长。当ω(z)=时,称为瑞利距离。
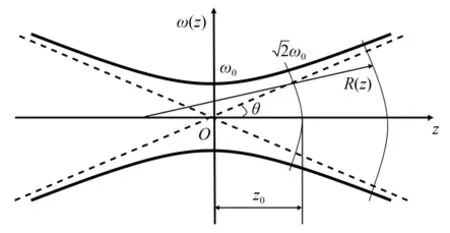
图1 高斯光束Fig.1 Gaussian beam
定义高斯光束光斑半径ω(z)随传播距离z的变化率为光束的发散半角θ(z)。当z→∞时,得到高斯光束远场发散半角,即:
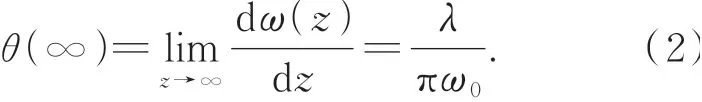
为方便研究高斯光束的传输变换规律,将高斯光束光斑半径ω(z)、等相位面曲率半径R(z)合为一个复参数q(z),即:
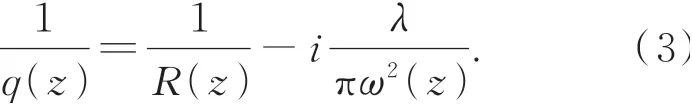
已知高斯光束在某位置的q(z),则可确定该位置处的ω(z),R(z),即:
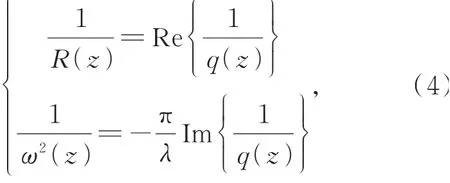
式中:Im表示取复数虚部,Re表示取复数实部。
高斯光束复参数q(z)的传播及变换规律遵守ABCD定律[9],即:

如果复参数q(z)的高斯光束顺次通过光学变换矩阵为M1,M2……Mn的光学系统,ABCD定律仍成立,该光学系统的光学变换矩阵M为:
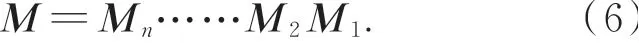
2.2 光纤阵列准直输出原理
图2为光纤阵列准直器结构示意图,它由光纤阵列与平凸微透镜阵列组成,光纤阵列端面与平凸微透镜阵列之间的距离为阵列耦合参数b。通过在光纤阵列与平凸微透镜阵列之间注入光学胶水实现二者的耦合,即采用光路有胶的封装方式。

图2 光纤阵列准直器结构示意图Fig.2 Structure diagram of optical fiber array collimator
以光纤阵列准直器单个通道为例,平凸微透镜的准直光路示意图如图3所示。光纤输出的光束近似为高斯光传输,束腰半径较小但发散角较大。利用平凸微透镜对高斯光束的变换作用,将光纤阵列端面出射的发散角较大的光束准直成发散角较小的近似平行光束。其中,P1为光纤阵列端面,b为光纤阵列端面与平凸微透镜阵列之间的距离,L,R分别为平凸微透镜阵列的厚度和曲率半径,P2为高斯光束出射后距离微透镜阵列曲面顶点d处的一个观察面。
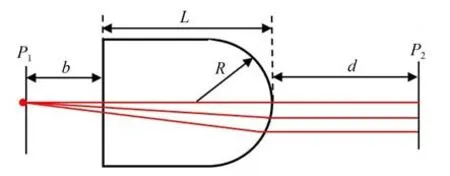
图3 单通道准直光路示意图Fig.3 Schematic diagram of single-channel collimated optical path
当光纤阵列与微透镜阵列之间注入光学胶水时,平凸微透镜对光纤出射高斯光束的光学变换矩阵T为:
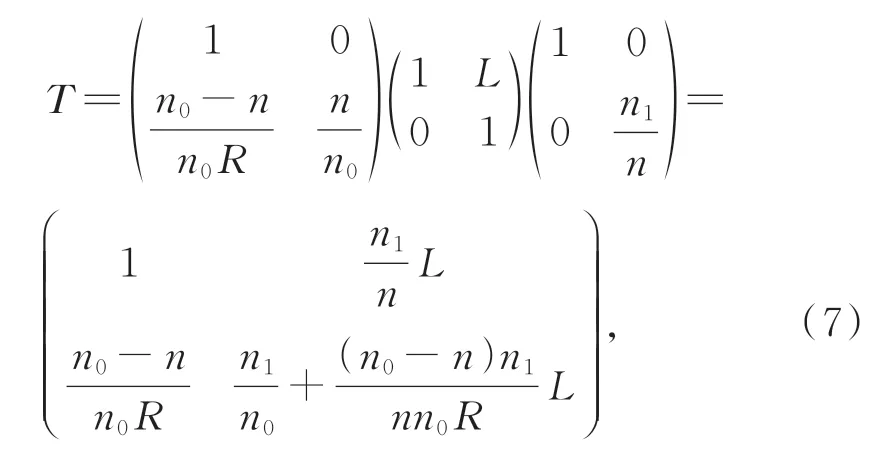
式中:n0为空气折射率;n为微透镜材料的折射率;n1为光学胶水的折射率。定义为平凸微透镜的物方截距[10]。
光纤阵列端面P1出射的高斯光束经由平凸微透镜出射到距离透镜曲面顶点d处观察面P2的整体光学变换矩阵M为:

光纤阵列端面出射的高斯光束用q表示为:

式中:ω为光纤阵列各通道光纤的模场半径,λ为工作波长。令则距离微透镜阵列曲面顶点d处的高斯光束的q为:
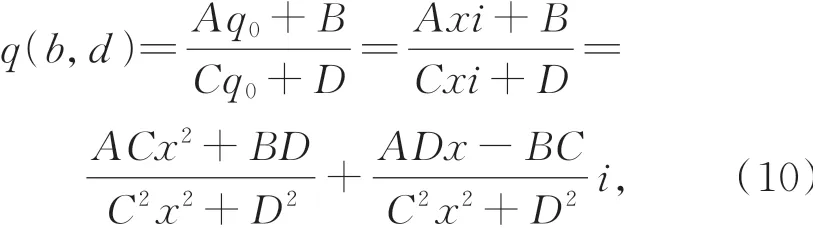
式中A,B,C,D为光学变换矩阵M的元素。根据高斯光束复参数q(z)通过光学系统的变换特性,可知观察面P2处高斯光束的光斑半径ω(b,d)与波面曲率半径R(b,d)为:
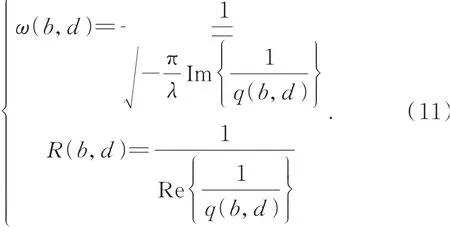
根据高斯光束的传输特性,经过平凸微透镜变换后的高斯光束束腰半径ω0与远场发散角θ分别为:
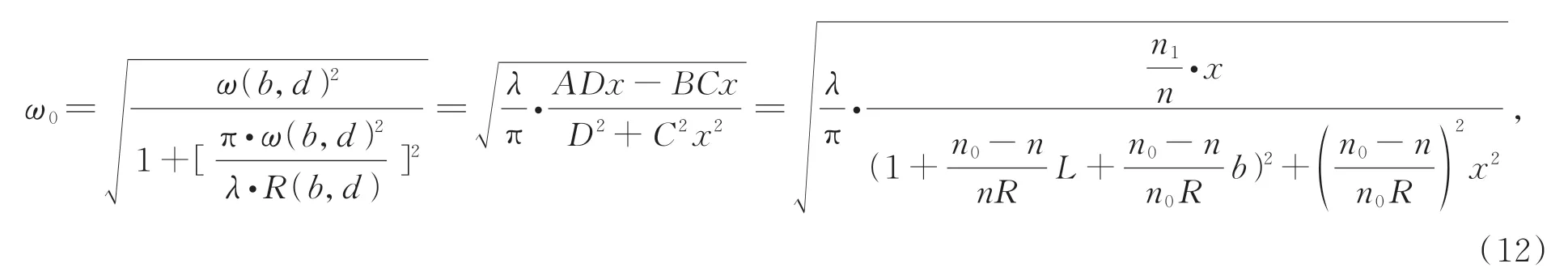

由式(12)可知,当微透镜阵列的相关参数确定后,变换后的高斯光束束腰半径ω0只与阵列耦合参数b有关。此外,高斯光束束腰半径ω0越大,远场发散角θ越小,光纤阵列准直器的准直效果越好。
2.3 光纤阵列准直器参数设计
通过Matlab软件进行数值模拟仿真,分析阵列耦合参数b对光纤阵列准直器准直性能的影响,从而确定光纤阵列准直器的设计参数。仿真参数设置如表1所示。
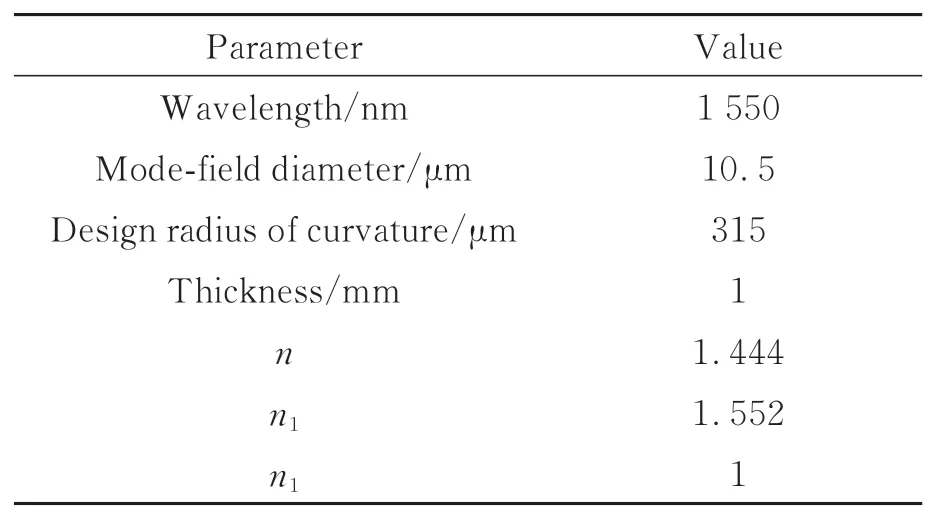
表1 光纤阵列准直器的仿真参数Tab.1 Simulation parameters of optical fiber array collimator
高斯光束束腰半径ω0与阵列耦合参数b之间的关系如图4所示。当阵列耦合参数b=0.026 mm时,光纤阵列准直器出射的高斯光束的束腰半径最大,ω0=83.06 μm,对应的远场发散角θ=0.68°。

图4 阵列耦合参数b与束腰半径ω0的关系Fig.4 Relationship between array coupled parameter and beam radius
进一步分析可知,当高斯光束的束腰半径ω0最大时,光纤阵列出射端面刚好位于平凸微透镜的物方焦点处,即当阵列耦合参数b等于平凸微透镜物方截距s时,光纤阵列准直器的准直效果最好。
当b=s时,式(12)可进一步简化成:

由式(14)可知,光纤阵列准直器准直后的高斯光束束腰半径ω0只与微透镜阵列的曲率半径R和光纤模场半径ω有关,而与微透镜阵列的厚度L无关。
为制备一维四阵元光纤阵列准直器,通过六维精密调整装置,实时调整光纤阵列与微透镜阵列之间的相对位置,而后注入光学胶水实现二者的耦合封装。光纤阵列参数及微透镜阵列参数如表2~表3所示,阵列耦合参数b=0.026 mm,光学胶水固化后在1 550 nm波长条件下的折射率为1.552。其中,光纤阵列采用V型槽法制备[11-12],微透镜阵列采用光刻胶热熔法制备。封装后的光纤阵列准直器实物图如图5所示,其头部主体尺寸为2.5 mm×2.5 mm×10 mm。采用光学设计软件Zemax对上述设计参数的光纤阵列准直器进行建模仿真,其准直光路如图6所示,准直效果良好。

表2 一维光纤阵列参数Tab.2 Parameters of one-dimensional optical fiber array
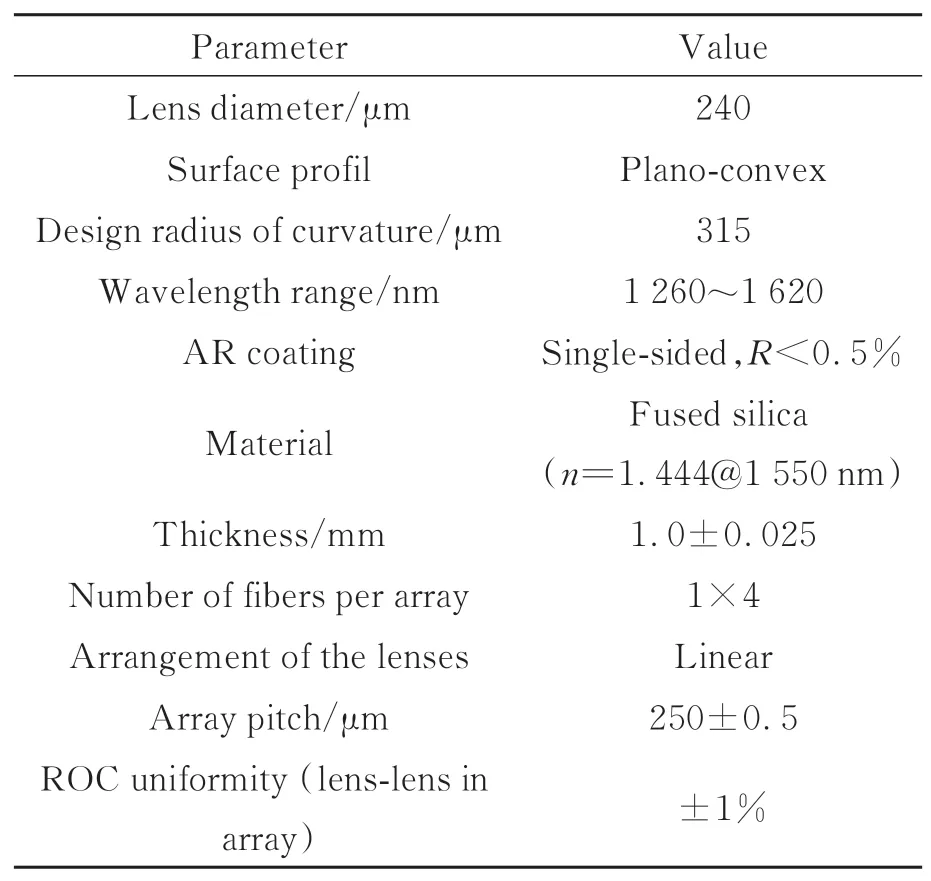
表3 微透镜阵列参数Tab.3 Parameters of microlens array

图5 光纤阵列准直器实物图Fig.5 Physical map of fiber array collimator

图6 光纤阵列准直器的Zemax光学仿真结果Fig.6 Optical simulation results by Zemax for fiber array collimator
2.4 理论设计误差
由式(14)可知,若忽略光学胶水及微透镜阵列材料的折射率误差,光纤阵列准直器出射后的高斯光束束腰半径ω0的理论设计误差dω0仅与微透镜阵列曲率半径R的公差dR及光纤模场直径ω的公差dω有关,则束腰半径ω0的理论设计偏差dω0为:
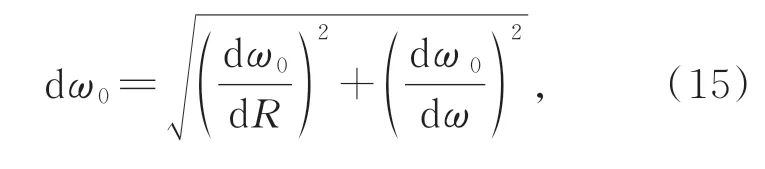
式中:

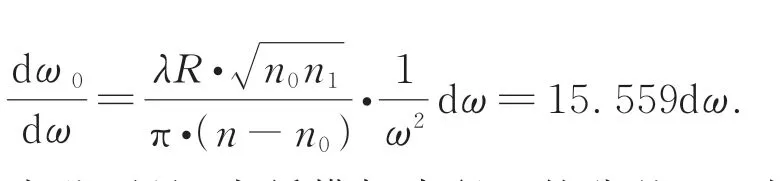
由此可见,光纤模场半径ω的公差dω对于光纤阵列准直器的准直性能影响较大。由表1~表2可知,平凸微透镜阵列的曲率半径R、光纤模场半径ω的公差dR,dω分别为3.15 μm(±1%),0.25 μm,计算得到高斯光束束腰半径ω0的理论设计误差dω0=3.975 μm,根据式(13)可得远场发散角的理论设计误差那么,设计的光纤阵列准直器的远场发散角为(0.68±0.03)°。
3 实 验
3.1 远场发散角测量
3.1.1 测量原理
为了评价光纤准直器的准直特性,需要测量其远场发散角。远场光斑法通过测得远场区域不同位置处高斯光束的光斑直径计算得到高斯光束的远场发散角[13-14]。为了准确测量高斯光束的远场发散角θ,定义L为从高斯光束高斯束腰到高斯光束发散角θ(z)=0.99θ处的距离,当因 此,采用远场光斑法测量高斯光束远场发散角时,需要保证测量位置大于7倍瑞利距离[15]。
光纤阵列准直器单个通道出射的高斯光束传播示意图如图7所示。取平凸微透镜曲面出射顶点为坐标原点O,高斯光束传播方向为Z轴正方向。其中,ω0为光纤阵列准直器出射高斯光束束腰半径;d为高斯光束束腰位置距离坐标原点的轴向距离;θ为高斯光束的远场发散角。

图7 准直器光束传播示意图Fig.7 Schematic diagram of beam propagation of collimator
假设在远场区域z1,z2两处测得的光斑半径分别为ω1和ω2,由式(1)可得:

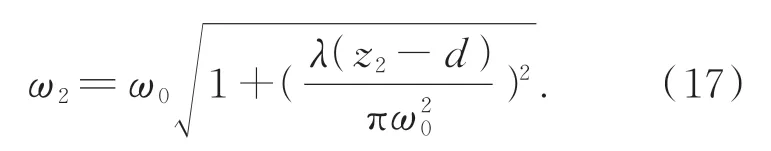
将式(16)和式(17)联立可得:
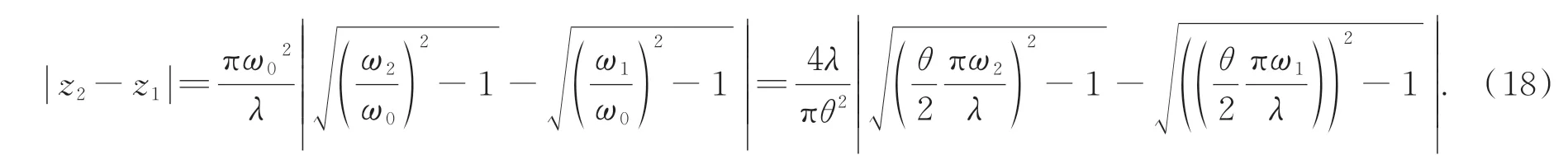
令Δz=|z2-z1|,由式(18)可知,通过测量相对距离Δz的两处位置的光斑半径ω1,ω2,可以求出光纤阵列准直器准直出射后的高斯光束束腰半径ω0及远场发散角θ。
该光纤阵列准直器出射高斯光束的束腰半径ω0理论值为83.06 μm,此时瑞利距离z0=因此,取距离坐标原点O的轴向距离140 mm处为初始测量位置。考虑到实际操作空间,距离太远,测试光源的光输出功率难以满足光束分析仪的探测要求,选定相对测量距离Δz=60 mm,即z2=200 mm。
3.1.2 测量装置

图8 高斯光束远场发散角测量装置Fig.8 Measuring devices of far-field divergence of Guassian beam
基于远场光斑法的高斯光束远场发散角测量装置如图8所示。该装置包括窄线宽激光器(Agilent 8164B)、多维度机械调节架、光纤准直器夹具、光学接杆组件、光学导轨和光束分析仪。待测光纤阵列准直器通过光纤准直器夹具固定在多维度机械调节架中,多维度机械调节架可以实现光纤阵列准直器六个自由度的调节。多维度机械调节架与光束分析仪分别通过高度可调节的光学接杆组件固定在光学导轨上。通过红外光显示卡辅助调整光束分析仪的高度,使光纤阵列准直器出射的高斯光束入射到光束分析仪的有效探测区域内。测量时,将多维度机械调节架固定在光学导轨中,通过光束分析仪在光学导轨中的左右滑动来改变与待测光纤阵列准直器之间的相对位置。测量过程中,所有元件都被安置在隔振光学平台上,且保证外界测量背景光不发生改变。
3.1.3 测量过程
激光器的工作波长为1 550 nm,输出光功率为4.25 mW,线宽典型值为100 kHz。光束分析仪为CINOGY公司CinCam系列光束分析仪,相机类型设置为CMOS-1203IR,响应波长为1 470~1 605 nm,可测 光斑直径 的为45 μm~4 mm。其配套软件在线监测界面如图9所示,设置光束分析仪光斑尺寸测量方法为“Fit Gauss”中的13.53%,即处的光斑尺寸。通过光束分析仪配套软件对各测量位置处高斯光束各参数数据进行读取与保存,可以读取光斑位置、光斑尺寸及椭圆度等信息。采用远场光斑法测量高斯光束的远场发散角时,首先调整多维度机械调节架使得各通道测量光斑的椭圆度均≥99%,保证测试光源正入射到光束分析仪的探测面,以长轴光斑尺寸Width Major作为各测量位置处的光斑直径2ω进行计算。
图9 软件监测界面Fig.9 Software monitoring interface
以光纤阵列准直器微透镜曲面出射顶点为坐标原点O,高斯光束传播方向为z轴正方向。移动光束分析仪在光学导轨上的位置,取距离坐标原点O轴向距离140,200 mm处作为测量位置点z1,z2,并将两处位置测得的光斑直径分别记为2ω1,2ω2,各测量位置处光斑直径均为20次测量的平均值,由式(18)计算得到高斯光束的束腰半径ω0及远场发散角θ的最佳估计值。由于式(18)为超越方程,故采用差分法由Matlab编程计算求解ω0及θ。
3.2 测量结果
采用远场光斑法依次测量光纤阵列准直器4个通道出射高斯光束的束腰半径ω0及远场发散角θ,测量结果如表4所示。光纤阵列准直器各通道的远场发散角θ分别为0.69°,0.67°,0.71°,0.68°,与远场发散角理论设计值0.68°的差值均在0.03°以内,即制备的光纤阵列准直器满足设计要求。同时,各通道保持了较高的一致性。
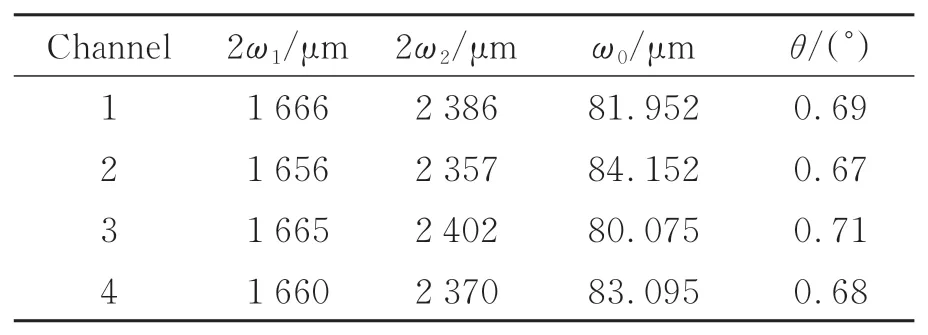
表4 通道参数测量结果Tab.4 Parameter measurement results of channels
3.3 测量不确定度分析
由式(18)可知,高斯光束远场发散角θ的测量误差源主要包括相对测量距离Δz的测量误差以及高斯光束光斑半径ω1,ω2的测量误差,且测量过程中多种误差源同时存在。在进行测量不确定度评定时,GUM(Guide to the Uncertainty in Measurement)方法基于不确定度传播规律,主要适用于线性模型。采用远场光斑法测量远场发散角的测量模型为非线性模型,采用GUM方法所需的偏导计算比较困难,因而本文通过蒙特卡洛法(Monte Carlo Method, MCM)评定远场发散角的测量不确定度。MCM在建立数学模型、设定输入量概率密度函数的基础上,通过对概率分布随机采样进行分布传递,确定输出量的概率密度函数,从而得到输出量的估计值、标准不确定度以及在指定包含概率下的包含区间,进而实现对测量不确定度的评定[16-17]。
光学导轨的定位精度为0.5 mm,光束分析仪的光斑测量误差为10 μm,且两类误差均符合均匀分布。已知均匀分布函数R(a,b)对应的概率密度函数(Probability Density Function, PDF)为以通道1为例,光束分析仪在测量位置点z1,z2处测得的光斑半径ω1,ω2分别为833,1 193 μm。采用Matlab MCM模型分析多误差源同时作用下的远场发散角测量不确定度的流程如下:
(1)MCM输入:定义远场发散角θ为输出量Y,相对测量距离Δz及高斯光束光斑半径ω1,ω2分别为相关输入量X1,X2,X3;输出量Y与输入量Xi(i=1,2,3)之间的模型为所推导的理论测量公式(18)。相对测量距离Δz及高斯光束光斑半径ω1,ω2均满足均匀分布,对应分布函数分别为RX1(59.5,60.5),RX2(828,838),RX3(1188,1198)。设置MCM试验样本量M为106。
(2)MCM传播:从输入量Xi(i=1,2,3)的PDF中 抽 取M个 样 本 值xi,r(i=1,2,3,r=1,2,...,M),并 对 每 个 样 本 向 量(x1,r,x2,r,x3,r)计算相应输出量Y的模型值。
(3)MCM输出及结果:将M个模型值按严格递增次序排序,并以200为子区间间隔绘制成直方图,得到输出量Y即通道1远场发散角θ的概率分布结果,如图10所示。多误差源同时作用下,远场发散角θ的测量值满足正态分布,远场发散角θ的估计值为0.69°,标准不确定度为0.01°,95%概率对称包含区间为[-0.02°,0.02°],即扩展不确定度为0.02°,此时包含因子为2。

图10 远场发散角θ的概率分布Fig.10 Probability distribution of far-field divergence angle θ
4 结 论
本文面向集成化、小型化阵列准直器的应用需求,提出了基于平凸微透镜阵列制备光纤阵列准直器的技术路线,详细阐述了其设计与性能评价的理论和方法。通过高斯光学和矩阵光学理论研究了平凸微透镜阵列对高斯光束的变换原理。基于光路有胶的耦合封装方式,推导了基于平凸微透镜阵列的光纤阵列准直器准直特性的解析表达式,仿真分析了阵列耦合参数对其准直效果的影响,为光纤阵列准直器的参数设计提供理论基础。最后,实验制备了四阵元光纤阵列准直器,并通过远场光斑法对其远场发散角进行测量。依据MCM方法对测量结果进行了测量不确定度的分析与评定。测量结果表明,光纤阵列准直器各通道远场发散角的测量值分别为0.69°,0.67°,0.71°,0.68°,扩 展 不 确 定 度 为0.02°,该测量结果均在设计容差(0.68±0.03)°之内。该光纤阵列准直器具有集成化高、性能指标一致性好、阵列易扩展、调试封装工艺简单等优势,为光通信领域中小型化、集成化的光纤阵列准直器提供了有效的技术手段。

