调频连续波激光雷达及数据采集信号链噪声分析

赵树华， 王玉冰， 张明时， 秦 莉， 宋俊峰， 王立军

（1.中国科学院 长春光学精密机械与物理研究所 发光学及应用国家重点实验室，吉林 长春 130033；2.中国科学院大学 材料与光电研究中心，北京 100049；3.吉林大学 电子科学与工程学院，吉林 长春 130012；4.鹏城实验室，广东 深圳 518055）

1 引 言

激光雷达具有体积小、分辨率高、抗干扰能力强、低空探测性能好等特点，广泛应用于军事［1］、测绘［2-5］、自动驾驶［6］、安防监控［8］等各个领域。调频连续波（Frequency-Modulated Continuous-Wave， FMCW）测距方法发射频率随时间线性变化的激光，回波信号与本振信号混频后产生频率与距离成正比的中频信号，通过分析中频信号的频率，即可获得距离和径向速度信息，具有距离分辨率高、抗干扰能力强等优势。此外，该方法所需的发射功率极低，通常在毫瓦量级。

2021年，Shi等利用双平行马赫-曾德尔调制器产生啁啾信号，实现单边带抑制载波调制的边带抑制比和边带载波抑制比均大于15 dB，搭建的FMCW激光雷达系统的测距分辨率为1.3 cm，测速分辨率为0.5 m/s［9］。2022年，Zhang等报道了一个128×128单元的光栅天线焦平面开关阵列的16 384像素的激光雷达，通过迭代学习获得的预失真电流波形线性调制，实现了距离分辨率为1.7 cm的三维成像［10］。2021年，Rogers等报道了一个512像素的相干探测器阵列的FMCW激光雷达系统，在17 m处实现了1.8 mm的测量精度，在75 m的距离上达到3.1 mm的测量精度。利用光子和电子单片集成技术，将密集的光学外差探测器阵列与集成的电子读出体系结构相结合，探测器阵列能够扩展到任意大［11］。2017年，Poulton等在300 mm晶圆的CMOS兼容平台上制造光学相控阵激光雷达，实现了低成本和紧凑型雷达片上技术，在2 m内距离分辨率为20 mm［12］。2019年，Zhang等提出了一种基于迭代学习预失真的激光扫频线性化方法，用于调频连续波光探测测距系统，在0.4 m的探测距离内实现了0.97 mm的距离分辨率［13］。2020年，Riemensberger等报道了一种基于孤子微梳产生线性啁啾信号的方法，实现了30通道并行测量的FMCW激光雷达，探测距离为10 m，距离分辨率为7.9 cm（192.1 THz）至5.9 cm（194.9 THz）［14］。上述激光雷达实现了较高的测速测距精度，但其数据采集方式都是基于商用示波器或数据采集卡，并没有自制激光雷达硬件电路。

在FMCW激光雷达中，以模拟-数字转换器（Analog-to-Digital Converter， ADC）为核心的中频信号采集模块是其关键组件，信噪比（Signalto-Noise Ratio， SNR）、信纳比（Signal-to-Noiseand-Distortion ratio， SINAD）和无杂散动态范围（Scatter Free Dynamic Range， SFDR）等参数是衡量该数据采集信号链交流特性的重要指标，并且直接决定着FMCW激光雷达的各项性能［15-16］。SNR反应了ADC信号链的噪声特性，影响着FMCW激光雷达的探测距离、动态范围、抗干扰和虚警概率等性能。然而，目前尚无针对FMCW激光雷达中数据采集信号链噪声特性的研究工作。

本文设计了FMCW激光雷达的数据采集信号链，基于该电路搭建了FMCW激光雷达系统，并且分析了该信号链的噪声水平，提出降低噪声的可行方法，能够为FMCW激光雷达设计提供参考。

2 实 验

本文以现场可编程门阵列（Field Programmable Gate Array， FPGA）芯片为主控制器，利用FPGA芯片的高速逻辑运算能力、超强的时序控制能力和丰富外设实现硬件设计［17］。

2.1 单端转差分电路

差分信号可以抑制信号传输路径中的共模电磁干扰，具备抗干扰能力；并且单端转差分电路作为ADC的缓冲器，与信号源进行了50欧姆阻抗匹配，为模数转换器ADC10D1000提供高频、低失真的模拟输入信号。本文选用差分放大器LMH6554作为核心器件，单端转差分电路设计如图1所示。其中，电阻R4和电容C7完成交流阻抗匹配，C7实现输入信号的交流耦合，中频信号经过差分放大器由单端信号转变为差分信号并由12，13脚输出，电阻R3，R6进行源端50 Ω阻抗匹配，吸收远端反射的电磁能量，保证信号的完整性。

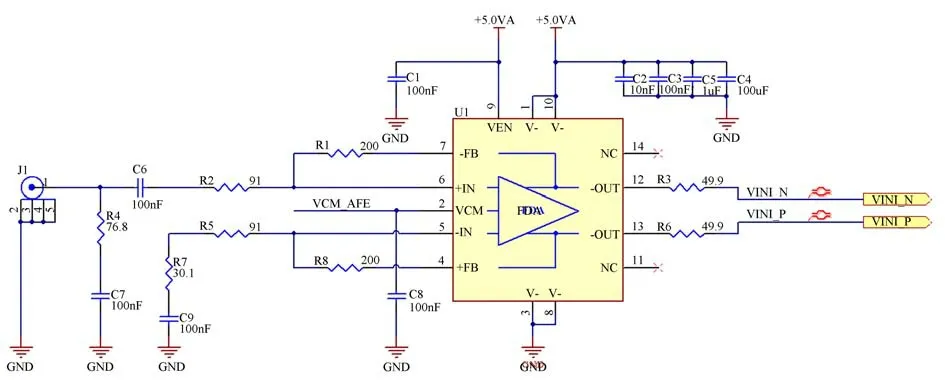
图1 单端转差分电路Fig.1 Single-ended to differential-ended circuit

2.2 模拟-数字转换电路

ADC10D1000是一款双通道10比特的高速ADC，单通道具有1 Gs/s采样率，其高采样率有利于获得高信噪比的频谱曲线。芯片基于时间插值原理，在双边沿采样和复用模式下，使用250 MHz采样时钟能够实现1 Gs/s的采样频率，功能设计如图2所示。其中，V5脚为双边沿采样开关，高电平下有效；D6脚为校准开关，低电平下有效，保证ADC在不同的工作温度、功率下的测量精度；Y3脚为满量程开关，高电平下量程为790 mV。

2.3 网络通信接口电路

为提高FMCW激光雷达的帧率，ADC采集的大量数据需要高速传输至上位机并进行数据处理，所以设计了基于TCP/IP协议的以太网通信接口，具有通信速率快、抗干扰能力强、兼容性好等特点。本文采用的以太网物理层收发器为KSZ9031RNXIC，是一种完全集成的三速（10BASE-T/100BASE-TX/1000BASE-T）以太网物理层收发器，使用标准CAT-6非屏蔽双绞线电缆发送和接收数据，实现了1000 Mb/s的传输速率。以太网通信电路如图3所示。

2～3，5～8，10～11脚分别连接至千兆以太网连接器HR911130A；36，37脚为SPI通信接口，37脚管理数据输入/输出，36脚用于MDIO（37）的输入参考时钟；19～24，27～28，31～33和35脚为RGMII通信接口，进行数据的输入/输出。

图2 AD转换电路Fig.2 AD conversion circuit

图3 网络通信接口电路Fig.3 Ethernet interface circuit

上述三个部分，在硬件层面上保证了信号的处理、数据的采集及发送。单端转差分电路作为ADC的缓冲器，避免ADC的动态阻抗对信号造成影响，并且将单端信号转为差分信号抑制共模干扰，满足ADC接口要求，此外还起到阻抗匹配、保证信号完整性等作用，为ADC电路提供高频、无失真的模拟输入信号；高性能ADC尽可能真实地还原了输入模拟信号，将连续的模拟信号转换为离散的、可数字处理的数字信号，该过程是上位机做快速傅里叶变换的基础；网络通信接口电路可以实现千兆的传输速率，保障ADC采集的大量数据高速、无误地传输至上位机，完成频谱分析等工作。

3 结果与讨论

3.1 ADC信号链测试

实验中，FMCW激光雷达使用的单边带调制器的调制速率为30 MHz/μs，当探测范围为150 m时，最大中频信号频率为30 MHz。根据香农采样定理，理论上60 Ms/s的采样率即可重建中频信号。另一方面，在过采样条件下频谱分析可以获得极高的数据处理增益，处理增益为，其中fs为采样率，WB为信号带宽。所以，为了最大程度降低底噪水平，ADC信号链的采样率应尽可能高。然而，过高的采样率对数据的缓存、传输和实时处理等提出了极高的要求，会显著增加系统的成本和功耗。综合考虑以上因素，配置ADC的采样频率为1 Gs/s。图4所示为输入信号幅度为350 mVp-p、频率为39.92 MHz时，ADC采集得到的时域波形和频谱曲线。其中，时域波形清晰地反应了测试信号的正弦特性；频谱曲线显示2～5谐波得到了充分的抑制。降低高次谐波对信号测试的影响，有利于提高ADC的SINAD参数，体现ADC信号链具有优异的交流特性。

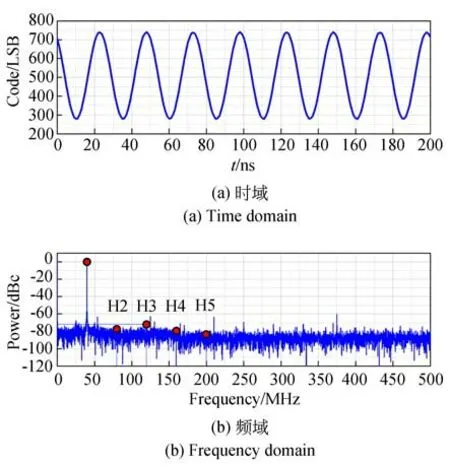
图4 ADC采集波形图Fig.4 Waveforms acquired by ADC

为了全面表征和分析ADC信号链的交流特性，在不同信号频率、不同信号幅度条件下，测试了ADC信号链的SNR，SINAD和SFDR。

为了避免频谱泄露对频谱分析的影响，测试信号频率分别为9.887 695 313，19.897 460 94，29.907 226 56，39.916 992 19，49.926 757 81，59.936 523 44，69.946 289 06，79.956 054 69，89.965 820 31和97.534 179 69 MHz；测试信号的 峰-峰 值 幅 度 为50～750 mV（-23.97～-0.45 dBFS），以50 mV为步进；除非特殊说明，本文采用8 192点进行快速傅里叶变换（Fast Fourier Transform， FFT）频谱分析。

图5为测试得到的SNR，SINAD和SFDR的分布。其中，将信号幅度归一化至0 dBFS。在关注的频率和幅度范围内，SNR与SINAD十分接 近，为37.7～56.4 dB，SFDR为53.1～69.5 dB，3个参数均随着输入信号的幅度增大和频率升高而迅速下降，这意味着系统噪声在快速升高会影响系统的交流特性。为了消除噪声对系统的影响，为后续优化设计提供理论依据，需要对ADC数据采集系统的噪声进行理论分析。

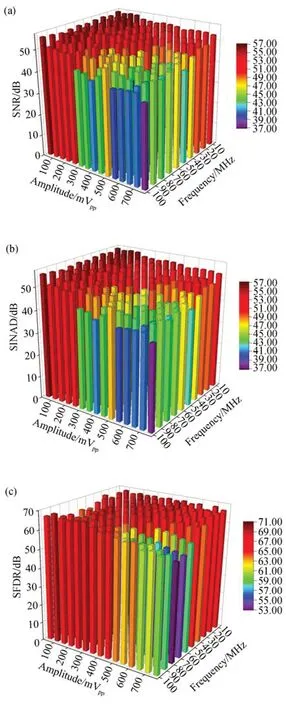
图5 （a） SNR、（b） SINAD和（c） SFDR的柱状图Fig.5 Distribution of （a）SNR， （b） SINAD and （c） SFDR

3.2 噪声分析

ADC数据采集信号链的噪声来源主要包含热噪声、量化噪声和采样时钟的相位噪声。

3.2.1 热噪声

热噪声是由导体中自由电子的布朗运动引起的，其频谱密度主要受温度影响，与频率无关，因此热噪声又称为白噪声。热噪声对于任何输入信号均恒定，但是量化噪声和相位噪声仅存在于交流情况下，所以可以通过统计直流信号的码字分布获得白噪声强度。实验中，使用50 Ω负载端接输入端口，统计了16 000个输出码字，如表1所示。

表1 ADC直流特性Tab.1 DC characteristics of ADC

由于热噪声是时间不相关的，其统计分布符合高斯分布。如图6所示，曲线为高斯拟合曲线，其标准差σ=0.59。热噪声均方根值为：

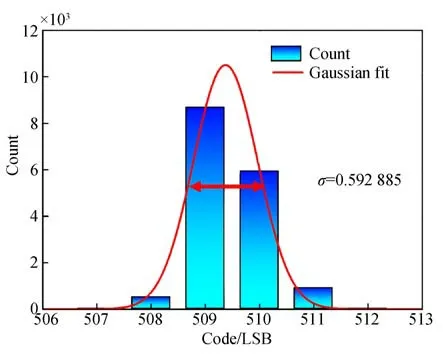
图6 ADC直流特性及高斯拟合Fig.6 DC characteristics of ADC and Gaussian fitting

3.2.2 量化噪声

图7为理想N位ADC的传递关系，模拟信号在±1/2 LSB范围内变化时，数字输出恒定，则产生一定的测量误差，这种量化误差称为量化噪声。由于量化误差在±1/2 LSB的范围内平均分布，则量化噪声的均方根值为：

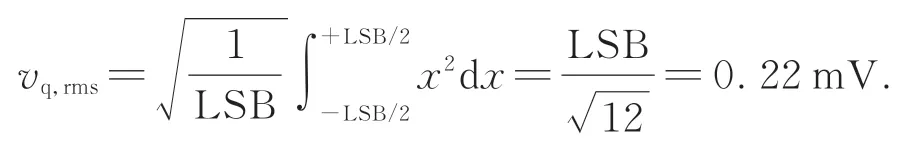
3.2.3 相位噪声与时钟抖动

受温度变化、供电纹波等因素的影响，采样时钟的相位存在快速、短期、随机的波动，导致时域采样边沿不稳定，即时钟抖动，在量化交流信号时存在一定的测量误差，该测量误差称为相位噪声，如图8所示。相位噪声主要表现为载波频点处出现裙边展宽，系统SNR降低。

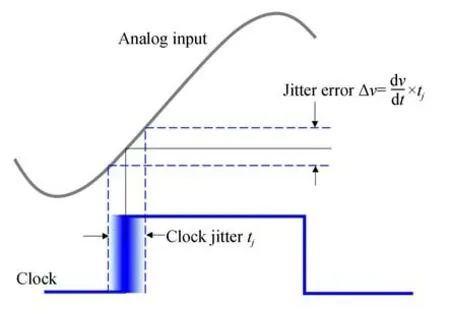
图8 相位误差与时钟抖动的关系Fig.8 Relationship between phase error and clock jitter

分析相位噪声的来源可知：输入信号的频率越高、幅度越大，相位噪声越显著。在分析相位噪声强度时，选择输入信号的幅度最大时（-0.45 dBFS，750 mVp-p）测得的SNR数据进行计算。

由于热噪声、量化噪声和相位噪声是彼此不相关的，所以系统噪声均方根值的平方等于3种噪声的均方根值的平方和，即：

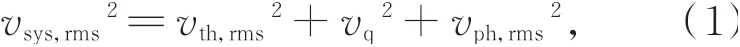
其中：vsys，rms为系统总噪声，vth，rms，vq，rms和vph，rms分别为热噪声、量化噪声和相位噪声。系统总噪声可由测得的SNR数据和输入信号幅度计算：

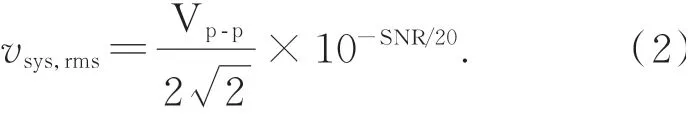
其中Vp-p为输入信号的峰-峰值。

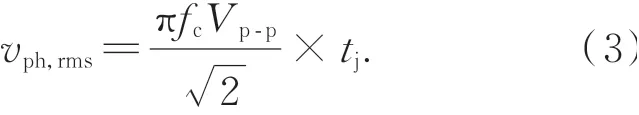
根据式（1）～式（3）即可计算系统相位噪声的幅度，并依据此获得时钟抖动的实验值，如表2所示。另一方面，FPGA设计工具Vivado中的混合模式时钟管理器（MMCM）IP核提供了精准的时钟抖动值，为13.7 ps，作为时钟抖动理论值。

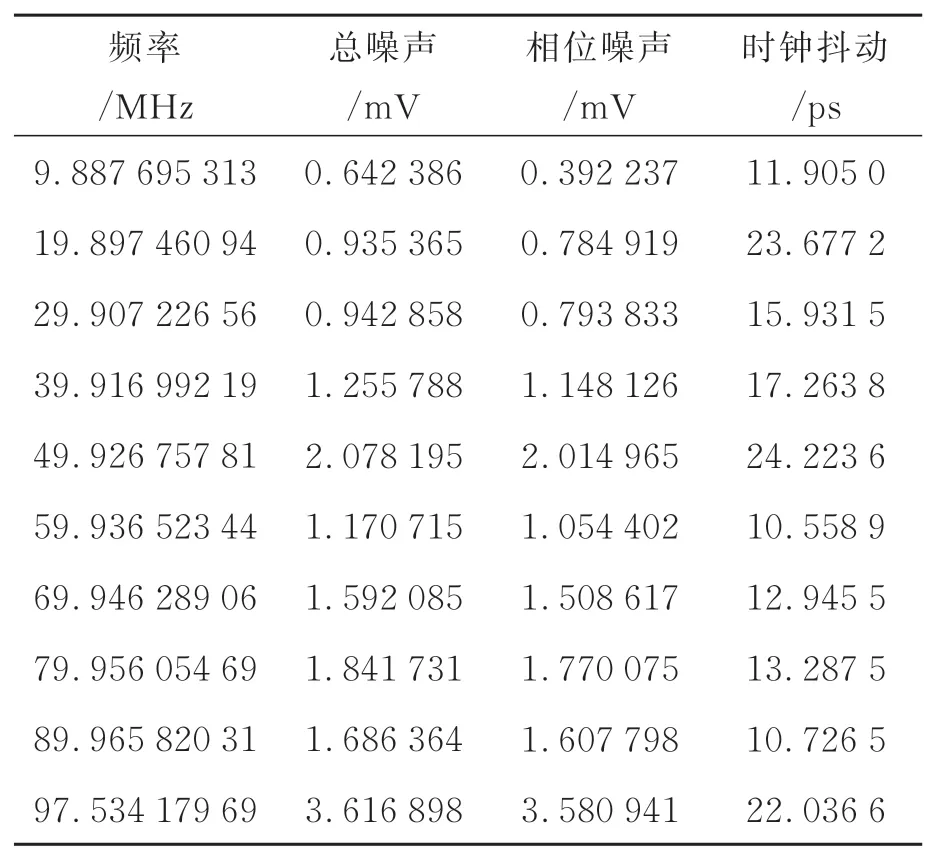
表2 不同频率输入信号的相位噪声和时钟抖动计算Tab.2 Calculation of phase noise and clock jitter of input signals

图9所示为信号幅度为-0.45 dBFS时，时钟抖动实验值随信号频率的变化曲线，时钟抖动平均值为16.3 ps，稍大于理论值13.7 ps，是由时钟走线与相邻数据线产生的电磁串扰导致的，可以通过增加走线间距、电磁屏蔽等方法解决。

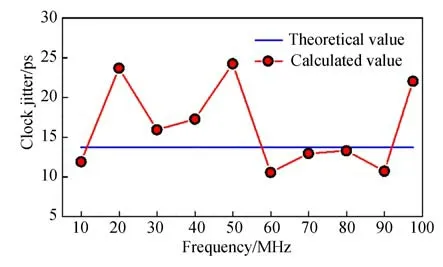
图9 不同频率下时钟抖动的计算值与理论值Fig.9 Calculated and theoretical values of clock jitter at different frequencies

由图9可知，与理论值13.7 ps最为接近的时钟抖动计算值为13.29 ps，对应的信号频率为79.956 054 69 MHz、幅值为750 mVp-p，此时系统的噪声组成如图10所示。噪声的主要来源是采样时钟的相位噪声，占总噪声的92.4%。

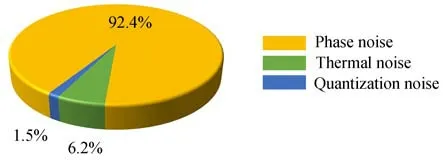
图10 噪声占比Fig.10 Proportion of noises

通过使用专用的时钟芯片降低时钟抖动，如LTC6950的时钟抖动为18 fs，由式（3）可计算当对应的信号频率为79.956 054 69 MHz、幅值为750 mVp-p时相位噪声为0.002 4 mV，与原有相位噪声（1.77 mV）、热噪声（0.457 4 mV）、量化噪声（0.222 7 mV）相比可忽略；由式（2）可计算出SNR为51.82 dB，提高8.65 dB，探测距离提高2.71倍。使用专用时钟芯片时使它靠近ADC芯片，用短而粗的走线，保障信号的完整性。

通过提高本振激光功率，使得光子散粒噪声远远大于电子学噪声总和，此时FMCW激光雷达能够获得量子效应限制的信噪比水平。然而，所需的本振光功率是需要仔细计算的，通常要求散粒噪声强度（ 2qIB）大于电学噪声的10倍：较低的本振功率无法获得量子效应限制限信噪比水平；较高的本振功率一方面徒增系统功耗，另一方面可能引发探测器的非线性效应。

3.2.4 引入数字滤波

为了降低相位噪声对测试结果的影响，引入了简单的数字滤波器，即将载波频率±4.88 MHz范围内的边带设为-100 dBc，滤除相位噪声产生的裙带展宽。在FMCW激光雷达中，通常取频谱曲线的峰值频率为中频信号的频率，所以该数字滤波器不会影响中频信号的频率测量结果，是一种简单、有效的中频滤波器，适用于FMCW激光雷达。

图11所示为加入数字滤波器后的SNR，SINAD随输入信号频率、幅度的变化图像。可以看到，在高频、大幅度条件下，数据采集系统的交流特性得到显著提升，SNR和SINAD的最小值分别为49.13 dB和48.90 dB，分别提高11.38 dB和11.32 dB，激光雷达的探测范围理论上能够提高3.7倍。

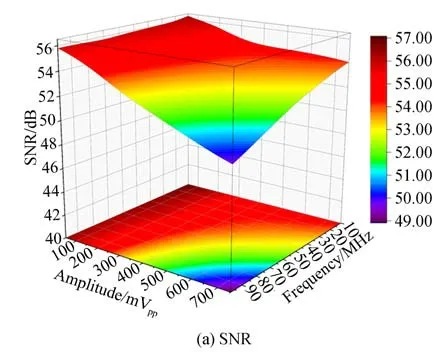
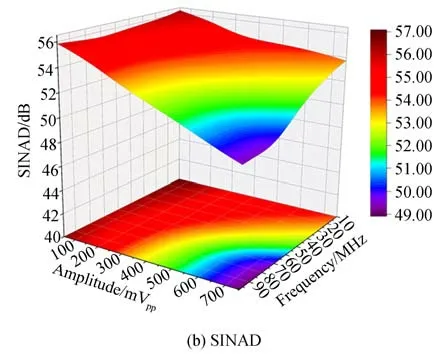
图11 滤波后曲面图Fig.11 Filtered surface diagram

4 FMCW激光雷达系统

最后，应用研制的数据采集信号链搭建了光学相控阵（Optical Phase Array， OPA）FMCW激光雷达系统。系统原理如图12所示，激光器发出单频、窄线宽激光；利用两级光纤放大器（EDFA）放大激光功率，射频源和单边带调制器，用于产生扫频激光［18-19］；然后，使用OPA芯片和透镜完成光束整形和发射；回波信号由准直器接收并耦合至光纤，利用2×2耦合器使回波与本振信号混频，并由平衡探测器检测并输出中频信号；为保护低噪声放大器，使用带通滤波器滤除能量较高的低频成分，其通带为3.5～54.0 MHz；最后，中频信号进入研制的数据采集系统并在上位机进行数据处理。

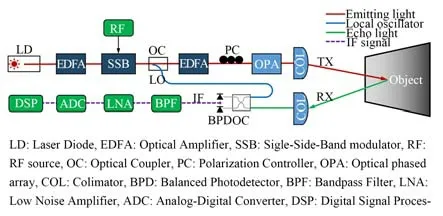
图12 FMCW 激光雷达系统结构Fig.12 Structure of FMCW lidar system

测试目标是面积为50 cm×50 cm、反射率为90%的标准反射板，目标的实际距离使用商用的激光测距仪标定。分别在5.139，10.594，25.169和40.416 m处进行测试，获得的频谱曲线如图13所示。随着距离的增大，中频信号逐渐右移。频谱左侧的快速衰减是由于带通滤波器的3.5 MHz低频截止频率导致的。障碍物的实际距离，其中fIF为中频信号频率，c为光速，Ts=100 μs为调制周期，fmod=3 GHz为调制带宽。注意，此计算数值包含了光纤长度、元件延时等诸多系统误差，分别计算4个距离下系统延迟误差，其平均值为17.479 m，测试结果应进行线性拟合并消除系统误差。测试结果如表4和图14所示，该雷达的测距误差最大为7.7 cm。

表3对比了不同激光雷达的性能，虽然以往研究实现了较高的测速、测距精度，然而其数据采集方式均基于商用示波器或数据采集卡。本文研制了激光雷达数据采集电路，并且理论分析了电路的噪声特性，为后续研究工作奠定了理论技术。

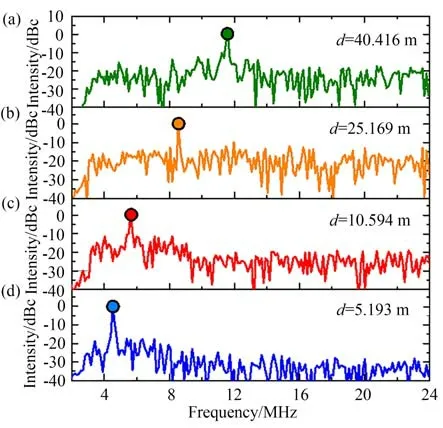
图13 不同距离目标测量频域谱线Fig.13 Frequency domain waveforms of targets at different distances

由图13（a）可知，在40 m距离时FMCW激光雷达实验系统依然具有10.39 dB的信噪比，所以障碍物的距离能够继续增加 1010.3910=3.3倍，即该激光雷达的探测极限约为133.67 m。如需进一步提高激光雷的探测范围，可以提高数据采集模块的采样率，依据数字信号的处理增益提高信噪比，或者降低数据采集模块的相位噪声，从而降低系统的总噪声水平。

表3 FMCW激光雷达对比Tab.3 Comparison of FMCW lidar

表4 不同距离目标的测量结果Tab.4 Measurement results of targets at different distances

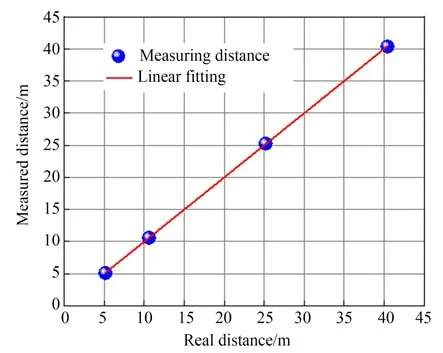
图14 FMCW 激光雷达测量结果Fig.14 Measurement result of FMCW lidar

5 结 论

本文设计用于FMCW激光雷达的中频信号采集模块，测试不同频率和幅值的输入信号的SNR，SINAD和SFDR，并分析数据采集信号链的噪声特性。首先，计算并分析了噪声组成和占比，指出高频高幅值情况下主要噪声源为相位噪声，计算了不同频率输入信号下时钟抖动为11～24 ps，抖动平均值为16.3 ps，稍大于FPGA芯片的理论时钟抖动13.7 ps。采用时钟芯片LTC6950（时钟抖动为18 fs）可将SNR提高8.65 dB，探测距离提高2.71倍。使用时钟芯片时使其靠近ADC芯片，用短而粗的走线，保障信号完整性。通过加入数字滤波器将SNR和SINAD分别提高11.38 dB和11.32 dB，获得了49.13 dB SNR和48.90 dB SINAD，对数据采集信号链的噪声优化及在激光雷达系统中提高探测范围具有参考意义。最后，将本文设计的中频信号采集模块接入光学相控阵FMCW激光雷达系统中，对50 cm×50 cm，反射率为90%的标准反射板进行5～40 m距离测量，测距误差最大为7.7 cm。对40.416 m距离目标仍具有10.39 dB的信噪比，由此计算，该激光雷达系统的探测极限约为133.67 m，可以通过提高数据采集模块采样率或降低系统的相位噪声进一步提高信噪比，扩大激光雷达的探测范围。本文的研究工作能够为FMCW激光雷达研究人员提供硬件设计参考，并且为电子学噪声计算提供依据，基于此可以计算出合适的本振光功率，为FMCW激光雷达设计提供理论参考。