基于热传导和卷积神经网络的磨床主轴热误差预测
王培桐, 范晋伟, 任行飞, 李 状
(北京工业大学 先进制造技术北京市重点实验室,北京 100124)
1 引 言
数控机床加工精度的影响因素很多,如热误差、几何误差、伺服误差等。其中,热误差是影响加工精度的主要因素[1]。为了进一步提高数控机床的加工精度,热误差建模和补偿方法成为近些年来的研究热点。
目前,经验建模法是热误差建模的常用方法,其模型是基于机床的实验测量。不同的模型结构已被用于机床热误差的预测,如多元回归分析(MRA)[2-4]、人工神经网络(ANN)[5-6]、模糊逻辑[7-9]、自适应神经模糊推理系统[10-11]、灰色系统理论[9]和不同建模方法的组合[12-13]。Chen等[5]使用多元回归分析模型和人工神经网络模型来补偿卧式加工中心的热误差。Zhang等[6]采用主分量法对建模变量进行优化,以避免温度敏感点之间多重共线性的影响。该方法预测机床热误差取得了较好的效果。章等[7]以某精密邸式加工中心为研究对象,利用智能温度传感器和位移传感器检测机床温度和主轴热变形。它通过新陈代谢模型对温度测点的数据进行前瞻预测。该方法改善了补偿滞后性的问题,从而提高了模型预测精度。Eskandari等[14]提出了一种利用离线技术补偿三轴数控铣床的位置、几何和热诱导误差的方法,热误差采用MRA,ANN和ANFIS 3种经验模型。为了更精准地建立预测模型,他们每10分钟收集一次实验数据,同时将实验数据分为训练数据集和检查数据集,模型预测精度得到了明显的提升,精度平均提高41%。Abdulshahed等[15]使用带有模糊c均值聚类的ANFIS建立了热误差模型。实验结果表明,所建立的热误差补偿模型可以将热误差降低到小于2 m。Wang等[16]通过模糊聚类方法对分布在机床上的20个温度传感器进行了优化,最终选取3个测点作为建模变量。不同种类的神经网络热变形预测方法与其他经验模型相比,具有较强的信息处理能力、并行处理能力和自学习能力。然而,单一神经网络热误差预测模型的缺点也很明显,如需要大量的学习样本、训练计算时间长,特别是“黑盒子”结果是不可解的。此外,机床工况条件一般是复杂的,热误差预测结果容易受到外界干扰。
针对上述局限性,本文提出了一种的基于热传导和卷积神经网络热误差的预测方法。首先基于热传导理论,推导出温差、热能增量以及热变形量的映射关系。通过主轴热仿真分析,揭示了主轴前后轴承端为主轴实际热误差源。然后,建立了以主轴表面温差为输入和主轴前后轴承端热变形量为输出的神经网络主轴热误差预测模型。最后,运用反向传播算法对该预测模型进行训练并确定最优参数。基于此方法,对磨床主轴进行了热误差补偿。该方法能够有效地预测主轴热误差,进而显著地提升数控机床的加工精度。
2 热变形本质
热变形的实质是物质体积随其所含热能的增加而增大的性质。根据热传导原理,单元体在t时刻的温度T(t)可表示为:
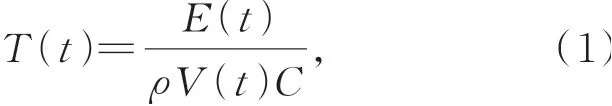
其中:V(t)表示t时刻单元体的体积,T(t)和E(t) 分别代表t时刻的温度和热能,ρ和C代表材料的密度和比热容系数,dx(t),dy(t),dz(t)分别代表材料的长度、宽度和高度。
t2时刻,单元体在x方向上的长度可表示为:
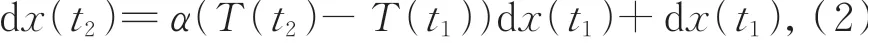
其中α代表热变形系数。
单元体t1到t2时刻在x方向上的热变形量可表示为:
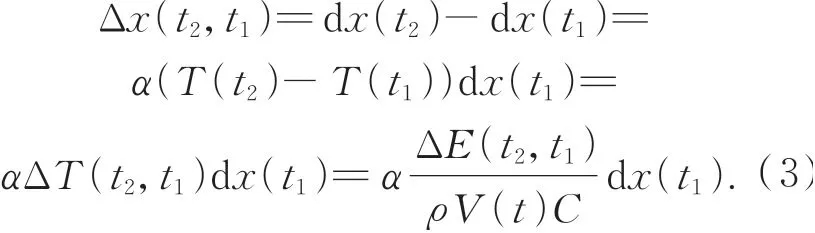
由式(3)可知,t1到t2时刻材料的热变形量主要由材料的热能增量或材料的温差所决定。
图1表示传感器对安装示意图(彩图见期刊电子版)。材料单元的每个表面都有两个相邻的球。蓝色的球表示材料表面的温度传感器,红色的球表示材料表面附近环境中的温度传感器。
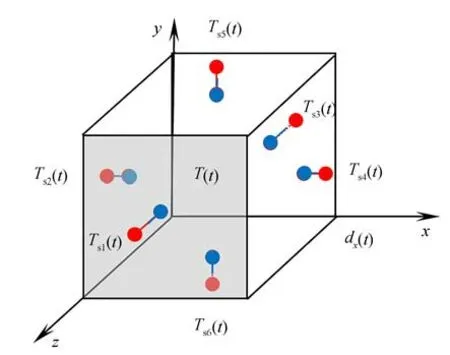
图1 t时刻微材料单元及其周围环境的温度Fig. 1 Temperature of micromaterial unit and its surrounding environment at t
此外,d代表每一对相邻的温度传感器的距离。材料单元从时间t到t+Δt在6个方向上的总的热能和温差可以推导出:
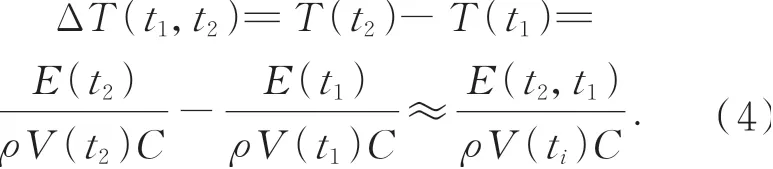
由式(3)可知,从ti时刻到ti+1时刻,总温度增量可表示为:
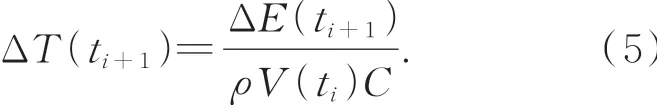
根据式(3)和式(5),ti+1时刻总的热变形量为:
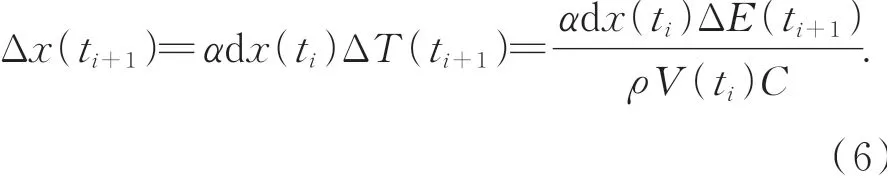
式(6)揭示了热能增量、温度和材料单元微小热变形之间的关系。热能的增量不仅取决于材料表面温度,还取决于材料表面与其周围环境的温差。因此,至少应该放置一对传感器来测量材料表面与其周围环境之间的温差,将温差作为输入变量,而不仅仅是表面温度。
2.1 主轴热变形分析模型
磨床主轴的具体结构参数如图2所示。它包括前后轴承、冷却导管和中心轴等部件。主轴总长为266.2 mm,外径为ϕ80 mm,中心轴直径为ϕ11 mm,轴承内径为ϕ12 mm。

图2 磨床主轴结构Fig.2 Structure of grinding machine spindle
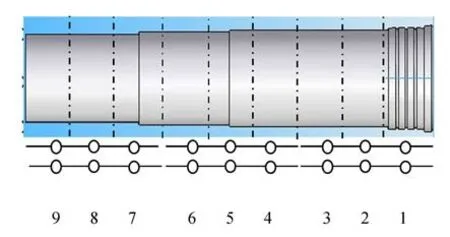
图3 传感器对分布Fig.3 Sensor pair distribution
为了准确地建立主轴热变形分析模型,将主轴等距地分为9段,每段间隔25 mm,如图3所示。第2段和第6段的表面与轴承内圈接触,第1,3,4,5,7,8,9段的表面与周围环境空气接触。沿主轴各段表面布置传感器对。内部传感器用于获取相关轴段表面的温度,外部传感器用于获取相邻环境的温度。
这里需要注意的是,主轴热误差预测模型忽略了不同轴段之间的直径差异。根据热变形、热能与材料温度的关系,主轴各段的热量增量可表示为:

其中:d表示传感器对间距离,D表示主轴直径,l代表每段主轴的长度,Taj(ti)表示ti时刻主轴第j段表面相邻的环境温度。由式(7)可知,k到k+1的热能增量由三部分组成。第一部分是热量的内部交换,内部的增减变化对总热能没有影响;第二部分代表主轴两端与其邻近环境的热量交换;第三部分代表每段轴表面的主轴与其邻近环境的热量交换。由此可见,主轴的热量增量还是由主轴表面与其周围环境的温差决定的。热能增加时,主轴各段的温差为:
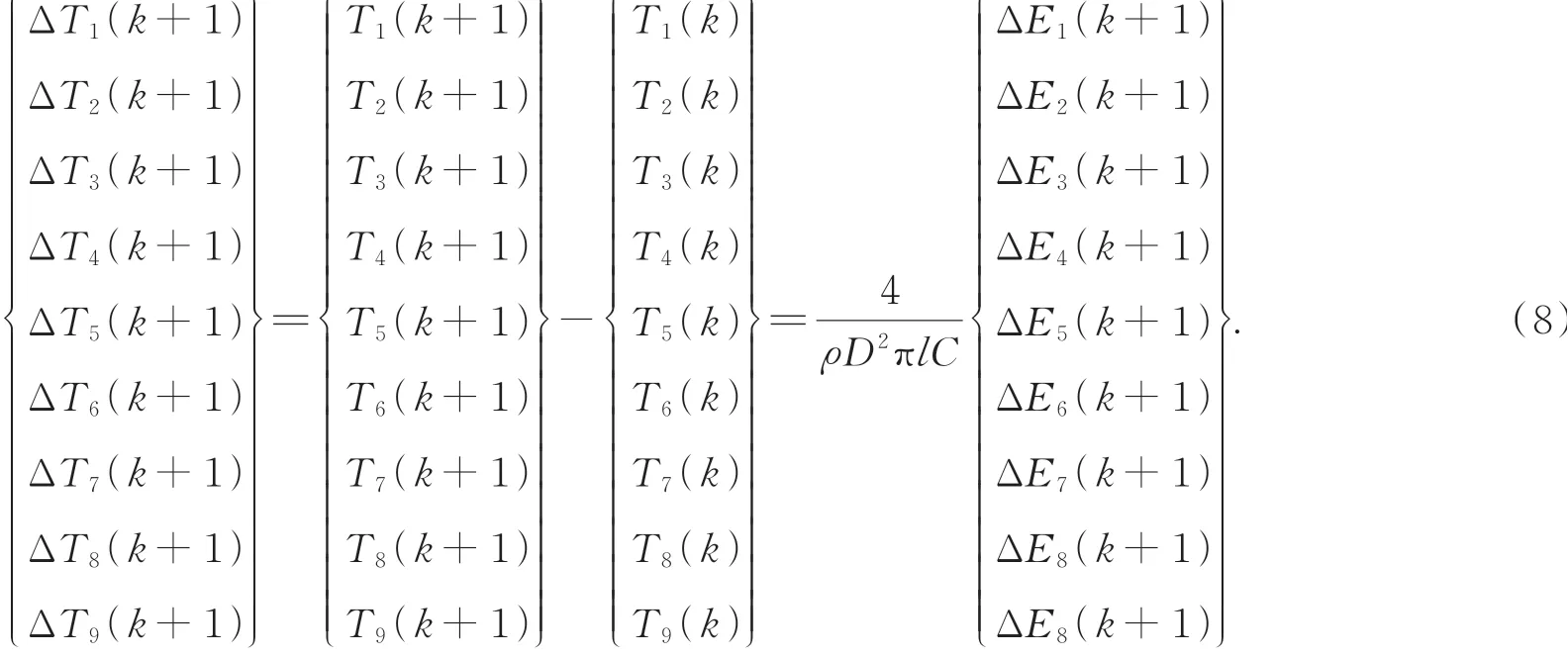
随着温度的变化,每个轴段的长度也会发生 变化,其增量可以表示为:

2.2 主轴热分析
通过数值模拟法直观地研究热能增量、温度和热变形量之间的关系。假设开始时主轴处于20 ℃的环境下,然后以1 500 r/min的转速驱动主轴运行100 min,最后使主轴自然冷却。仿真过程的采样频率为20 Hz,α=1.2×10-5/℃,材料密度ρ=7.85×10-6kg/mm3,比热容系数C=460 J/(kg·℃),材料内部热能传导系数λ=5.02×10-2J/(mm·℃·s),在材料表面及其相邻空气处,热能传导系数λa=0.025×10-3J/(mm·℃·s),传感器对间距离d=25 mm,主轴直径为11 mm,轴向传感器间隔25 mm。
轴承的摩擦在轴承内部几乎全部转化成热量,因而致使轴承温度升高,轴承热量Q计算如下:
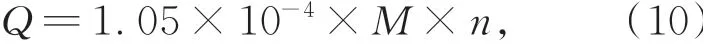
其中:n为转速,M为摩擦力矩。前轴承的摩擦力矩为54.5 N·m,后轴承的摩擦力矩为52.5 N·m。
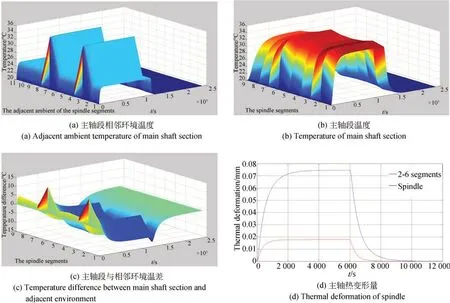
图4 主轴热分析结果Fig.4 Thermal analysis results of spindle
图4(a)~4(c)为0~12 000 s内各主轴段与其相邻环境之间的温度变化和温差变化。仿真结果表明,虽然主轴各部分表面温度基本相同,但各部分的环境温度变化较大。由此可见,主轴第2段和第6段的温度偏差高于其他主轴段。这是因为主轴段的第2和第6分别代表前轴承的后端面和后轴承的前端面。砂轮的定位精度取决于前后轴承的定位精度。这意味着前后轴承的综合热误差是主轴的热误差源,而不是整个主轴的热伸长量。图4(d)展示了主轴和2~6段的热变形。当主轴转速为1 500 r/min时,主轴和2~6段的热变形趋势大致相同。因此,研究主轴2~6段的热变形对主轴热误差的预测具有重要意义。
3 基于热传导卷积的神经网络热误差建模方法
3.1 基于卷积热传导的神经网络模型要素架构
从第2.1节可知,主轴表面与其周围环境的温度差作为输入变量,它代表主轴输入的热能。然后内部的热能在主轴内部从高向低传导。热能的外在表现为主轴的温度和变形具有固定的关系。因此,在构建来自主轴不同部位的神经网络模型时,应以主轴各段与其周围环境的温差作为输入。主轴的前部、中部和后部对应于不同的神经节点。在这里输入的温差应首先转化为热能,而不是在主轴中进行热交换时的相互混合。考虑到热能传导的迟滞性,这意味着需要建立卷积神经网络模型。为了使热能更均匀地分布,该模型需要利用另一神经网络层使热能更大幅度地混合,然后使混合的热能转变为主轴的温升和热变形。最后,神经网络的输出层应以时间为变量,来预测主轴在不同时间下总的热变形量。
3.2 热误差预测模型架构
主轴热误差预测模型如图5所示。除了第0层外,模型总共有3层。在第0层,有9个输入ΔTi(t)(i=1~9)。随后,每个输入的温差被转化为一个热能增量在这里进行卷积处理。在第1层中,有9个输入节点对应于9个主轴节段,每个热量增量混合并输入,使第2层中各个轴段的热量充分交互。第2层有3个节点,对应的前,中和后部分的主轴,积累的热能增量会在这里充分混合,然后热能增量以热变形量作为第2层的输出。在第3层中,通过混合和放大第2层的各输出参数,同时考虑热能随时间的指数变形规律,最终给出了预测的热误差值。和yi分别代表第i项 采 样 数 据,[y0,y1,...,yM-1]则分别代表一组M个数据样本。然后用矩阵A[j]表示神经网络中第j+1层输入和第j层输出。

图5 神经网络架构Fig. 5 Neural network architecture
第0层的输入放大因子矩阵K[0]可表示为:

第0层的输出矩阵A[0]可表示为:

在主轴热误差的实际预测中,考虑到第i组温度偏差数据会受到第i-1组温差数据的累积影响,层0处的第i组输出可以表示为:
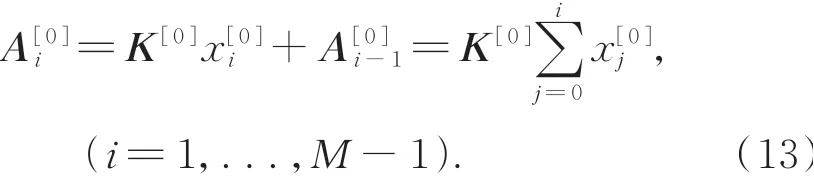
第j(j=1,2,3)层的输出A[j]可表示为:
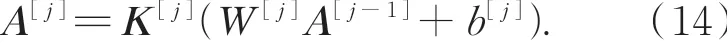
第1~3层的放大因子如下:其中需要优化参数k。
冷料斗为拌和站出厂时设置完成,每年由厂家安排人员进行重新校核。在几年的使用过程中不曾进行移动,且进料数量符合要求。
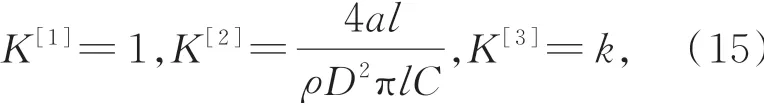
从式(11)可以看出,神经网络第1层的输入是每个轴段温差转换成的热能增量。这些累积起来的混合热能会在神经网络第二层转化成热变形量。神经网络的第三层将混合热变形乘以一个放大因子,最终得到热误差预测值。
3.3 反向传播算法
本文采用反向传播算法来确定热误差预测模型参数的最优值。如图6所示,初始参数为每个前轴承的摩擦力矩为54.5 N·m,每个实际轴承的摩擦力矩为52.5 N·m。热变形系数α=1.2×10-5/℃,材料密度ρ=7.85×10-6kg/mm3,比热容系数C=460 J/(kg·℃),内部材料的热能传导系数λ=5.02×10-2J/(mm·℃·s),在材料表面及其邻近空气的热能传导系数λa=0.025×10-3J/(mm·℃·s)。
为了确定预测模型的参数值,引入损失函数L和总的损失函数J,分别为:
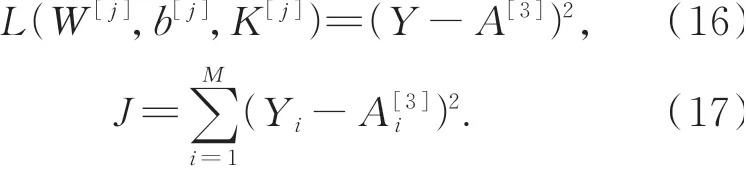
通过实测输入和输出数据,利用反向传播算法对建立的神经网络模型进行学习和训练,以此来调整分布权重W[j],偏差b[j]和激活函数K[3]。对激活函数、权重和偏差进行修改如下:
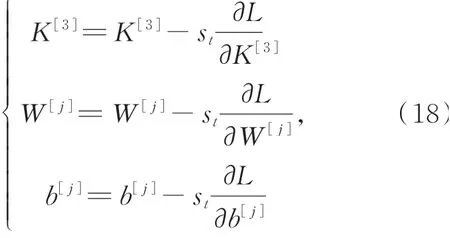
其中st表示学习步长。当损失函数L<ζ或者学习步长大于st,该程序终止。
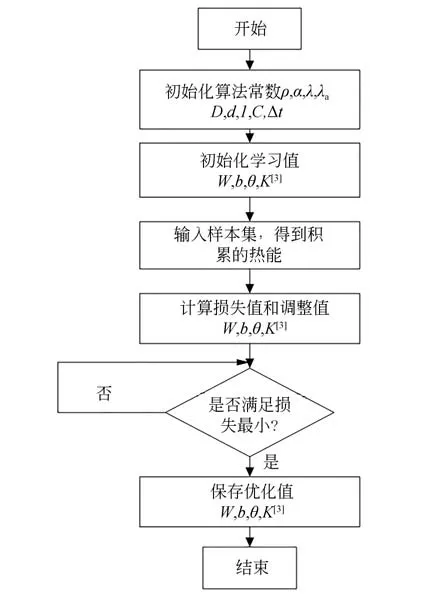
图6 神经网络训练流程Fig. 6 Flow chart of neural network training
4 实 验
4.1 实验仪器
在主轴热变形实验中收集主轴各段表面与其周围环境的温差。电热偶传感器如图7(a)所示。利用红外仪器采集主轴各段的离散温度数据,如图7(b)所示。然后,使用YanHua 8211总线温控数据采集模块将收集到的温控数据发送到计算机。最后,采用电容式传感器来测量主轴的热变形系数,如图7(c)所示。测量仪器参数列于表1。

表1 主轴热变形测量仪器Tab.1 Measuring instruments for thermal deformation of main shaft

图7 电主轴的温度测量Fig.7 Temperature measurement of motorized spindle
4.2 热误差预测模型验证
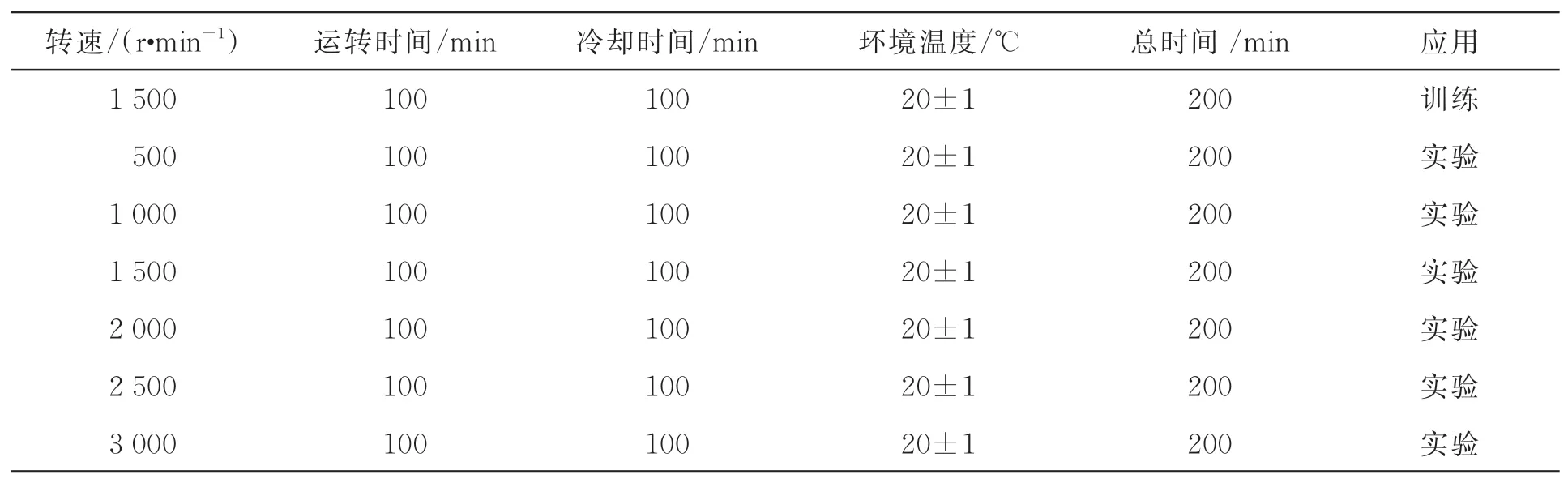
表2 主轴热变形测量实验参数Tab.2 Experimental parameters for thermal deformation measurement of main shaft

表3 综合测试试验参数Tab.3 Comprehensive test parameters


图8 不同转速下主轴热变形实验结果Fig.8 Experimental results of spindle thermal deformation with different rotation speeds
由实验结果可以看出,当转速为3 000 r/min时,主轴热变形预测的最大残差仅为5.7 μm,其他转速下的预测残差均小于4.3 μm。特别是在综合试验中,热变形的最大预测残差甚至小于2.7 μm。也就是说,主轴的运行时间越长,热变形的预测精度就会更高。因此,最大热变形量取决于主轴转速,转速越高,最大热变形量越大。本文提出的热误差预测模型的精度较高。
4.3 热误差补偿实验
在验证1~2段主轴热变形预测模型有效性的基础上,进行了轴类零件磨削热误差补偿实验。从图9可以看出,选择磨削加工的轴。在实验中,对AC,AD,AE,ED的尺寸误差进行检测,以验证热误差补偿的有效性。

图9 磨削轴原理Fig.9 Schematic diagram of grinding shaft
图10为热误差补偿系统,该系统主要包括控制器和驱动两个模块。对象链接和嵌入技术是计算机中不同软件间数据交换的应用。过程控制OLE(OPC)是一种国家标准,用于控制器与计算机之间的信息交换。OPC统一体系结构(OPC UA)是由SINUMERIK 840D数控控制器基于SIMATIC网络服务器和PROFINET(过程现场总线网)的技术。在热误差补偿研究中,开发了一套OPC UA客户端软件。其中,由NCU的MC插值器组织块92[OB92]计算Z轴位置设定点。其补偿原理是将Z轴的理论位置设定点值和当前时间预测热变形值之和作为当前Z轴设定点。考虑到插值器[OB92]每2 ms运行一次,热误差预测程序每隔50 ms运行一次,意味着插值器应将其设定的插值间隔增加25倍,以达到相同的频率。当热误差预测程序更新热误差值时,插值器将选择新的热误差值作为补偿值。考虑到热误差的变化速度足够慢,热误差补偿的精度足够高。
图11为轴类磨削实验现场。采用两种热误差预测方法对磨床主轴进行补偿,方法一为单一神经网络热误差预测方法[7],方法二为本文提出的热误差预测方法。
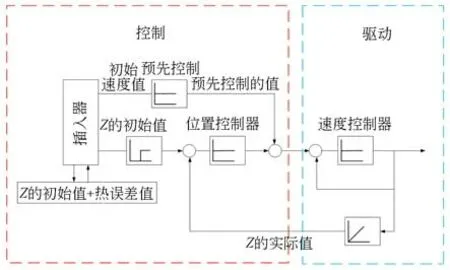
图10 基于OPC UA的热误差补偿方法Fig.10 Thermal error compensation method based on OPC UA

图11 轴类磨削实验Fig. 11 Shaft grinding experiment

表4 热误差补偿结果Tab.4 Thermal error compensation results
通过不同主轴热误差补偿后磨床的加工精度如表4所示。结果表明,工件的加工尺寸AE在Z方向上的加工误差由0.004 3 mm减小到0.002 3 mm。方法二相较于方法一,补偿精度提高了46.5%。AC和AD的绝对位置分别减小了0.001 0 mm和0.001 6 mm,加工精度分别提高了41.7%和43.2%。工件的加工精度得到了明显提升。因此,实验证明了本文提出的热误差预测方法比单一神经网络热误差预测方法的预测精度更高,热补偿效果更好。
5 结 论
本文提出了一种基于热传导和卷积神经网络的主轴热误差预测方法。首先,利用温度传感器测量主轴表面与其周围环境的温差,将输入温度差乘以热传导参数转化为热能增量。然后,将每个轴段获得的热能增量彼此混合。最后将第2~6段主轴热变形量作为输出。根据热传导理论,建立了主轴温差、热能增量以及热变形量之间的映射模型,并通过仿真确定了主轴前后轴承是实际的热误差源。在此基础上,基于神经网络法建立了主轴热误差预测模型。实验结果表明,综合测试中模型预测的最大残差小于2.7 μm。将提出的热误差预测方法和单一神经网络热误差预测方法应用到实时热误差补偿中。比较补偿结果可以得出,本文提出的主轴热误差预测精度较高,且补偿后机床加工精度得到明显提升。本文提出的主轴热误差预测方法不仅局限于磨床,对其他类型的机床也同样适用。

