一种基于视觉分析的指针式仪表智能抄读方法

戴 威，陆小锋，钟宝燕，赵梓辰，刘学锋

(1.上海大学 通信与信息工程学院，上海 200444；2.上海大学 计算机工程与科学学院，上海 200444)

0 引 言

电气化工厂的电气室中存在数量较大用于表征电气设备工作状态的指针式仪表，对这些仪表进行识别和记录需要耗费较多的人力成本，并且由于人为因素可能会造成误检、漏检的情况，电气室设备发出的辐射对人体健康也会产生一定影响。如今，在人工智能领域的飞速发展时期，涌现出各种基于机器视觉的智能识别系统。其中，电气室巡检机器人通过机载相机对仪表进行图像采集并进行相应视觉分析得到检测结果，实现了电气室设备的智能化管理[1]。

基于指针定位的思想对指针仪表进行识别是现今的主流方法[2-7],即通过检测预处理后的图像中的指针位置来确定读数[8]。饶源[2]通过对预处理后的二值化图像进行Hough变换直线检测来分割指针，但不足之处在于易受表盘冗余字符区域干扰，导致识别结果出现偏差。检测到指针后，再通过角度法或者距离法来识别读数，对此张文杰等人[3]通过手工标记与最小二乘法结合的方法来表示指针角度与读数的对应关系，但此方法的泛化能力一般，当被检测仪表规格不同时，最终结果误差较大。距离法的原理是利用指针与相邻刻度之间的距离来判读示数[5]，只有当图像质量比较高时，得到的计算结果才比较准确。

当前，深度学习方法广泛应用在无人驾驶、医疗诊断和工业检测等领域并已取得较好的效果[9-12]，并且得益于该类方法非常强大的特征提取能力、无需对现有数据进行繁琐的预处理，为机器视觉提供了一种端到端的检测模型[13-14]。此外，当今硬件科技的发展水平也能为该类方法提供强大的支撑，高性能的硬件和由此带来的计算能力也能符合深度学习应用于众多实际场景的需求[15-16]。因此，已有一部分人着手研究基于深度学习理论的指针仪表检测识别方法。张增光[17]使用MASK RCNN网络模型对指针仪表进行读数识别，但对于复杂背景等因素的鲁棒性较差。贺嘉琪[18]同样使用了MASK RCNN网络模型进行仪表提取，并采用了阈值分割和概率霍夫直线检测对指针进行拟合定位，然后采用KNN对仪表读数判定，但准确率不太理想。彭昆福[19]采用Faster R-CNN算法和G-RMI算法对指针仪表进行检测识别，再通过深度回归方法对示数进行判读，准确率较高，但方法计算代价较大，执行时间较长。Cai W等人[20]提出对仪表图像进行指针旋转从而扩充数据量并通过一个CNN直接回归指针示数，但此方法对图像的质量要求较高。

综合上述情况，该文提出一种基于视觉分析的指针式仪表智能抄读方法。该方法通过利用深度学习中主流神经网络方法之一的YOLOv3对图像中的仪表进行特征提取，然后再通过仿射变换、基于霍夫变换概率直线检测和极坐标变换的距离法分别进行后续的图像畸变矫正和仪表示数判读。实验表明，该方法在准确度、鲁棒性和检测效率上能满足工程要求。

1 指针仪表识别方法

1.1 基本流程

如图1所示，首先，通过特征提取网络YOLOv3对包含仪表指针的图像进行刻度数字的特征点提取，从而将仪表区域从原始图像中分割出来，并得到刻度数字的位置信息。考虑到仪表图像有较大可能由于采集时的角度倾斜而出现畸变效应，需采用仿射变换进行畸变矫正处理，在最大程度上减少后续示数判读误差。然后，通过基于霍夫变换概率直线检测和极坐标变换的距离法对矫正后的图像进行示数判读。

图1 指针仪表识别方法流程

1.2 基于YOLOv3的表盘关键点提取

YOLOv3使用Darknet-53网络结构去除最后的全连接层，剩余52个充当主体网络的卷积层，可被分为三个阶段，结构类似金字塔网络(FPN)，其中前26层为阶段一，第26层感知野小，负责检测小目标；第27至43层为阶段二；第44至52层为阶段三，第52层感知野大，负责检测大目标，网络结构如图2(a)所示。在部分网络层中引入了快捷链路(Shortcut Connections)，其正对应了该网络模型中使用残差网络(Residual Network)来优化网络参数，其中左侧数字代表框内网络层所使用残差块的数量。一个残差块由两个卷积层、两个激活函数和一个快捷链路构成，如图2(b)所示。

(a)Darknet-53网络结构 (b)残差块结构

图2 YOLOv3神经网络结构

YOLOv3以图像作为输入，采用回归的方式进行目标预测，不需要预先提取目标候选区域，直接通过神经网络提取特征参数，以向量的形式输出目标物体所在图像中的定位和类别信息，并能够输出13×13、26×26和52×52的3种尺度特征，既保证了检测效率，又改善了针对小目标的检测性能。因此，首先通过YOLOv3神经网络进行仪表关键点提取。

1.3 基于仿射变换的仪表图像畸变矫正

由于图像采集设备在对场景内仪表进行拍照时，摄像头所在平面与待检测仪表所在平面呈一定倾角关系，所以经过YOLOv3神经网络提取出的仪表图像并不是正视视角下的常规仪表，直接用于示数判读会产生误差。因此，需要先对关键点提取后的仪表图像进行基于仿射变换的畸变矫正，即通过空间变换将倾斜仪表图像矫正为正视视角下的仪表图像。当成像距离较近且倾角斜偏下方时，投影变换的矫正方法尤为适合，当成像距离较远时，投影变换将近似为仿射变换，并且此时用于变换所需的图像固定像素点个数由4个减少为3个。

仿射变换是一种二维坐标到二维坐标之间的线性变换，它保持了二维图形的“平直性”(直线经过变换之后仍然是直线)和“平行性”(二维图形之间的相对位置关系保持不变，平行线仍然是平行线，且直线上点的位置顺序不变)。任意的仿射变换都能表示为乘以一个矩阵(线性变换)，再加上一个向量(平移)的形式，变换所用矩阵计算公式如式(1)所示，经过仿射变换进行畸变矫正的仪表图像如图3所示。

(1)

图3 畸变矫正前后对比

1.4 基于距离法的仪表示数判读

距离法的基本思想是通过计算仪表图像中线状指针与其左右相邻刻度线之间的间距来确定指针读数。假设指针左侧相邻刻度线的像素是a1,a2,…,an1，指针右侧相邻刻度线的像素是b1,b2,…,bn1，线状指针与其左侧相邻刻度线的一个像素记为ai，与其右侧相邻刻度线的一个像素记为bi。

由距离公式可得到指针直线与刻度线像素ai的距离为dai，再依据公式(2)计算指针示数：

(2)

其中，R表示指针的示数，k1表示指针左侧的刻度线对应示数，k2表示指针右侧的刻度线对应示数。上述方法的大量计算较大程度保证了距离法的准确性，距离法的基本原理与人工判读的方法存在一定的区别，人工判读方法重点关注相邻刻度线与指针直线之间的弧度来确定指针示数，距离法则侧重相邻刻度线与指针直线之间的垂直距离。

鉴于此，距离法判读指针仪表示数的关键主要有两点，第一点是基于线状指针中心轴线平行于左右相邻刻度线的假设，第二点是检测到的刻度直线关键点位置信息与刻度示数关键点位置信息之间的对应关系。针对第一点，待检测的指针仪表刻度盘呈圆弧状，可矫正仪表图像中包含刻度的部分，以便于确定仪表指针位置的示数，如图4(a)所示。针对第二点，可通过霍夫变换概率直线检测的方式对刻度直线进行检测，得到刻度直线的关键点位置信息，并且霍夫变换需要极坐标系下的输入图像。极坐标变换一般适用矫正图像中的圆形目标，通过坐标变换关系式(公式(3))将仪表图像由直角坐标系变换至极坐标系，再结合YOLOv3网络提取的刻度示数关键点位置信息进行仪表示数判读。

(3)

如果圆心为极坐标原点，那么直角坐标系中的圆将变换为极坐标系中的直线。故仪表图像在直角坐标系中的圆弧形刻度将变换为极坐标中的直线刻度，变换后的仪表图像如图4(b)所示。

图4 仪表坐标变换前后对比

2 实验分析

2.1 实验设置

实验中所用的计算机平台配置：操作系统Windows 10 Professional x64，Intel(R)Core(TM)i7-4790 CPU @3.60 GHz，内存为16 GB，显卡为NVIDIA GTX 1080Ti，工控机开发语言为Python，深度学习算法部分用到的框架为PyTorch1.7.1。上位机端向巡检机器人端发送巡检指令，巡检机器人接收到指令后，再通过内至工控主机处理摄像头采集到的仪表图像进行视觉检测。

2.2 实验数据及预处理

为了体现仪表实际所处场景的复杂性，训练所需数据集由巡检机器人的超清摄像头采集获得，设置调整摄像头姿态角度、位置及环境光照，以确保采集到不同倾斜角度和不同光照条件下的仪表图像，共计1 000张，再通过数据增强的方式扩增该数据集，具体操作类型有翻转、旋转、镜像和高斯白噪声等，扩充后的数据集共有4 000张仪表图像。再将数据集按照8∶1∶1的通用标准划分为3 200张训练集、400张验证集和400张测试集，并且依据VOC数据集格式将训练集和验证集进行人工标记。用设计好的网络训练预先自制的仪表图像数据集，得到用于提取仪表图像关键点的YOLOv3神经网络模型。

2.3 评价指标

为了准确判断模型对指针仪表表盘关键点的提取效果，分别从模型检测的准确率(ACC)、精确率(PRE)和召回率(REC)三个指标来评价模型效果。ACC为检测图片中准确识别到指针仪表表盘图片数量所占比例，PRE为准确识别的图片数量占全部检测为指针仪表表盘图片数量的比例，REC为准确识别的图片数量占全部指针仪表表盘图片数量的比例。设Nt为准确识别的图片数量，Nall为所有检测图片数目，Nf为误检测的图片数量，No为漏检测的图片数量。则ACC、PRE和REC的计算公式为：

(4)

为了表明该方法在仪表畸变矫正前后示数判读上的识别效果，将人工读数记为Ia，并以其为基准，算法读数记为Im，算法读数与人工读数之间误差值记为Δ，示数判读的准确率记为mAP，则计算公式如式(5)所示：

(5)

为了体现该方法在具体应用于工程实际问题中的实时性，即方法执行时间，将其记为tm，其主要由三部分组成，分别为表盘关键点提取时间，记为te，畸变矫正时间，记为tt，以及示数判读时间ti，计算关系如式(6)所示。

tm=te+tt+ti

(6)

2.4 结果分析

(1)指针仪表图像的提取。

为了表明基于YOLOv3神经网络用于指针仪表图像进行关键点提取的准确率和检测方法的鲁棒性，设置了不同的实验条件，分别为正常光照、暗弱光照、过曝光照和包含椒盐噪声，并将以上4种条件下指针仪表图像提取的实验结果作对比，如表1所示。

表1 4种条件下指针仪表图像的提取结果

表1中，在4种条件下对于400张待检测图片的提取结果表明，该网络方法的准确率较高，且鲁棒性较强，其中，正常光照条件下的检测效果最好，准确率高达96%，而其他三种条件下的检测性能分别出现不同程度的下降，尤其是图像中包含椒盐噪声时，检测准确率与正常光照条件下相比下降了10.50百分点，其主要原因在于YOLOv3神经网络对于噪声干扰较敏感，但对于实际场景中出现该类噪声的概率较低，故该检测方法仍具有较大的适用性。

考虑到实际应用场景中可能不只会出现环境光照和噪声干扰的情况，还可能会出现采集姿态不同而导致检测结果出现偏差的情况，故实验部分还分别补充了3种主要的采集姿态条件下的检测结果，如表2所示。可看出对于仰视、平视和俯视共计三种采集姿态下的仪表图像，该方法依旧能够有效提取到仪表刻度数字的关键点。此外，为了降低采集姿态带来的视角误差，还需对仪表图像进行后续必要的倾斜畸变矫正。

(2)畸变矫正前后的示数判读。

对仪表图像数据集中400张测试集图片进行检测识别，分别测试记录仪表图像进行畸变矫正前后的算法自动读数，并与作为参考的人工读数进行对比，得出误差值和准确率，表3所示为其中10组数据结果。

表2 不同条件下三种采集姿态图像的提取结果

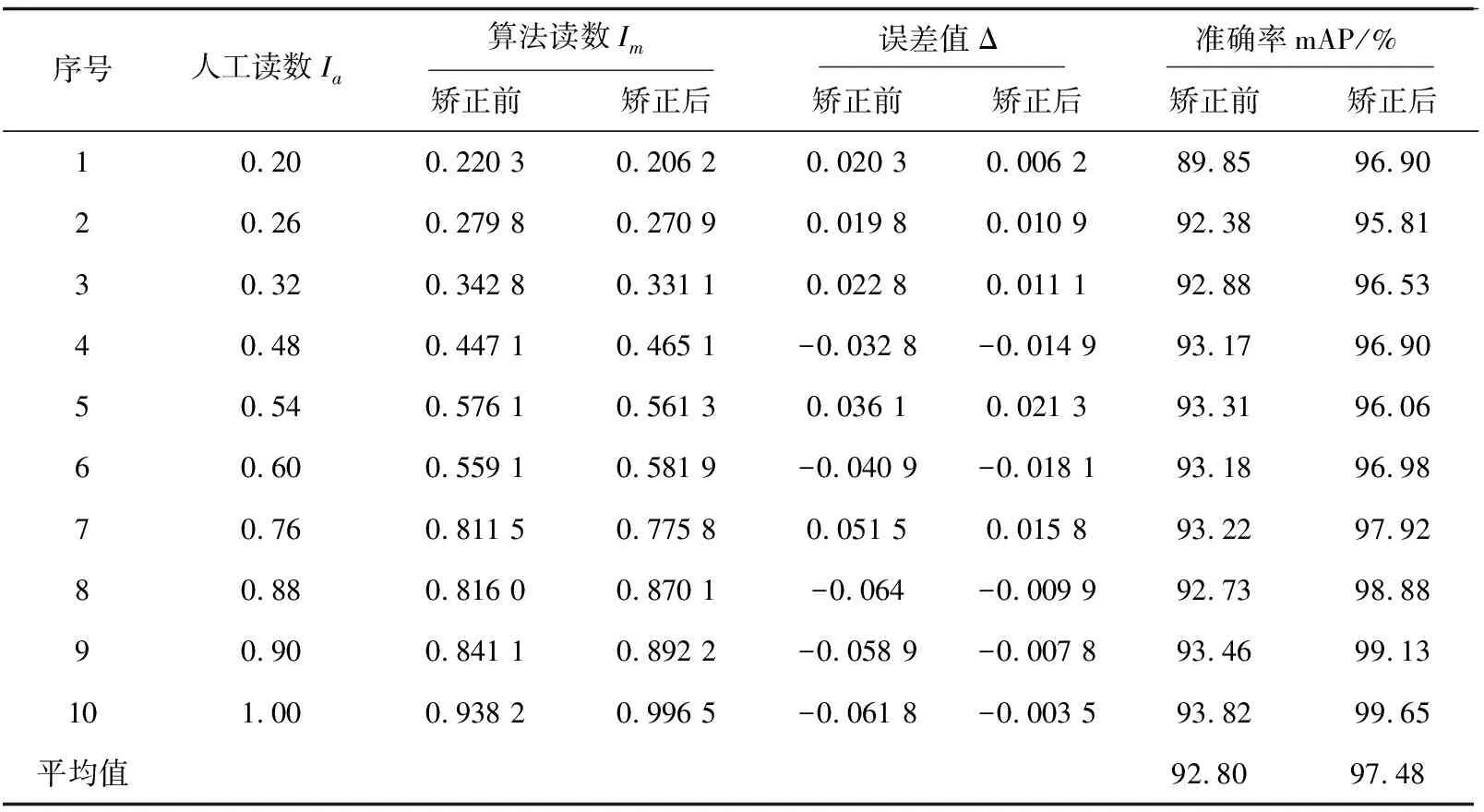
表3 畸变矫正前后的示数判读结果

表3中，1～3组数据为采集图像的姿态处于仰视状态下得到，则所得数据结果略微偏大，误差值为正值；4～7组数据为近似平视状态下采集得到，则所得数据结果存在概率性偏大或偏小，误差值有正值和负值；8～10组数据为俯视状态下采集得到，则所得数据结果略微偏小，误差值为负值。

从上述具有代表性的10组数据结果中可看出，该方法在示数判读的准确率上矫正前后的平均值分别为92.80%和97.48%，这主要表明两点，第一，该方法用于指针仪表图像的畸变矫正是具有较显著的作用，能够有效提升算法读数的准确率；第二，该方法在指针仪表读数图像检测识别上的平均准确率为97.48%，能够满足工业检测的需求。

(3)方法执行时间。

本部分实验记录分析了指针仪表图像数据集中400张测试图片的各步骤检测所花费的平均时间，如表4所示，可看出方法检测时长主要耗费在指针仪表关键点提取阶段(125 ms)，方法总计耗费时长为245 ms，即方法检测帧速率可达到4 fps，能够满足工业检测实时性要求。

表4 方法执行时间

(4)方法先进性分析。

为了验证该方法的先进性，利用已有3种性能较为优异的方法做同样的检测实验，几种方法用于检测的主要步骤为关键点提取和示数判读，并将各方法的评价指标结果作对比，如表5所示。

表5 方法检测性能对比

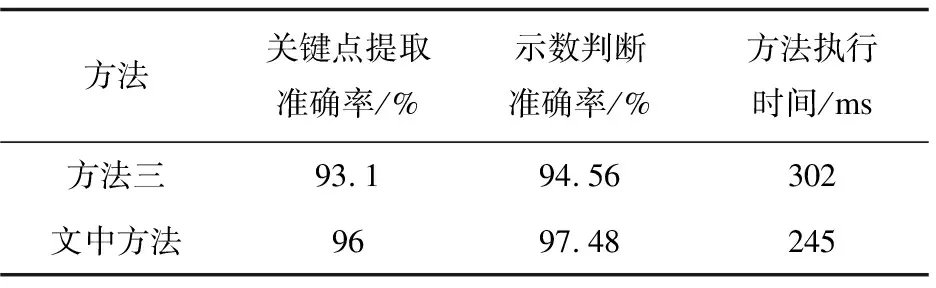
续表5

通过与3种现有方法的实验对比，可看出文中方法在各个评价指标上均优于其他三种方法。方法一为模板匹配法+Hough变换法，方法二为Faster R-CNN+Hough变换法，方法三为改进SSD+CNN。方法一基于传统图像处理，相比其他方法，在检测准确率和方法执行时间上均存在显著不足，主要原因是模板匹配法对于图像要求质量高、抗干扰性差，并且算法计算量较大。方法二、方法三和文中方法在检测准确率上较为接近，但在检测时间上，方法三和文中方法要优于方法二，这主要是因为在目标检测框架上，SSD和YOLOv3均属于one-stage方法，相较于方法二中的R-CNN(two-stage方法)，在处理速度上有较明显优势。总体来讲，文中方法在检测准确率和方法执行时间上均有优良的性能表现，能够更好地满足实际工程问题的需要。

3 结束语

提出了一种新的用于电气室设备中指针式仪表识别与示数判读方法，该方法基于YOLOv3深度学习视觉神经网络进行仪表图像的关键点提取，并根据实际检测场景中出现的畸变、弱光、噪声以及其他干扰情况进行了相应的仿射变换矫正处理，最后通过基于霍夫变换概率直线检测和极坐标变换的方式对仪表图像使用距离法进行示数判读。经过多次实验验证，该方法能够实现对仪表的自动读数识别，在拍摄时的姿态角度、距离等方面具有良好的兼容性。同时，相较于传统机器视觉方法和现有的基于深度学习方法，该方法在多尺度特性检测问题上的表现更优，即当采集到的图像中待检测目标区域较小时，得益于YOLOv3网络的多尺度特性，该方法仍能准确检测识别指针仪表。最后，该方法在识别准确率和检测效率上能够满足实际需求，对于电气化工厂的安全生产具有重要意义。