基于TFM模型的滞留气团数值模拟方法及PIV试验研究

罗爽，陈奇，刘霞，蒋劲*，彭宇

(1. 武汉大学动力与机械学院，湖北 武汉 430072； 2. 湖北省水利水电科学研究院，湖北 武汉 430070； 3. 湖北省水利水电科技推广中心，湖北 武汉 430070)

在泵站等输水系统的有压管路中，管线的局部高点处通常会出现气体滞流形成气团的现象，如果管内的滞流气团不能充分排出，水流的冲击作用则会使滞流气团被压缩，容易导致严重的爆管事故.

关于输水管路中的滞流气团，国内外学者开展了大量的研究工作.HOLLEY[1]对管内滞流气团的形成以及压力波动进行了研究，指出阀门突然开启将造成气团的压力剧增，这是由于在水流的冲击作用使滞流气团被压缩.POTHOF等[2-3]对下倾管路中的滞流气团进行研究，得出了管径和下倾管长对滞流气团运动行为的影响.此外，还基于动量守恒和能量守恒构建了滞流气团的流体动力学模型，可以较为准确地预测下倾管路中气体的流动特性.郑源等[4]对含有滞留气团输水管路进行了系统研究，其研究结果表明，当无法确定有压管内滞留气团的体积时，可采用刚性水锤模型进行计算，且计算结果与气团大小无关.LIU等[5]提出了虚拟弹性数学模型，可有效降低特征线法对气液交界面进行动态追踪时的插值误差，但对于气团较小的流动，弹性模型相对于刚性模型并没有明显的精度优势.富友等[6-7]建立了考虑管壁参数的气液两相流一维双流体模型，分析了相间驰豫现象的微观机理和相间作用的构建方法，但该模型主要适用于气相含量较低的管路系统数值计算.文献[8-9]通过VOF模型对管内水流冲击滞流气团的现象进行了数值模拟，通过与试验结果对比发现，VOF模型可以较为准确预测气团形态变化和流场的压力波动.马佳杰等[10]采用不同的湍流模型对含有滞流气团的管路流场进行了分析，发现RNGk-ε模型的预测效果较好，可以较准确地给出压力波动结果.

目前，该领域研究主要针对于滞流气团对管路系统瞬变特性以及宏观流动特性的影响，而对于滞流气团局部流场及运动行为方面的研究则相对较少.文中基于双流体模型(TFM)构建局部高点处的气-液两相流场数值模型，并通过粒子图像测速系统(PIV)对滞流气团的流场进行测量，验证该数值模型的合理性，从而为研究滞流气团流场特性及运动行为提供新的数值模拟方法.

1 数值模拟

1.1 数学模型

目前，对于管路中滞流气团的流场模拟，多采用VOF模型追踪各控制体内的气相体积分数；该方法的局限性在于，液相和气相在流场的数值模拟中共用一个动量守恒方程，相间交互作用没有动量的交换，仅考虑体积分数的影响.为克服VOF模型的局限，文中通过TFM模型来构建滞流气团的气-液两相流场，在该多相流模型体系下，气相和液相均通过独立的N-S方程组进行描述.在数值模型的构建中，将空气视为理想气体，假定相间无热量和质量交换，则该流场数值模型的基本控制方程组为

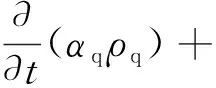
(1)

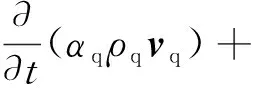
(2)

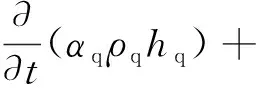
(3)

上述式中：下标p，q为相编号；t，α，ρ，v，p，g，h和Q分别为时间、物相体积分数、物相密度、速度矢量、静压值、重力加速度、焓值以及热通量.

对于动量守恒方程式(2)中的应力-应变张量，通过式(4)进行描述，即

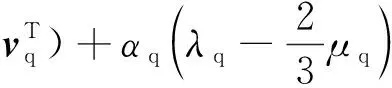
(4)

式中：μ和λ分别为物相的剪切黏度和体积黏度；I为单位张量.

对于气相和液相的动量交换，文中通过文献[11]提出的数学模型来确定式(2)动量守恒方程中的交换系数Kpq.该模型主要适用于气泡形状多变的气-液两相流动，计算式为

(5)

式中：CD为曳力系数；Ai为拖曳作用面积；dp为气相的泡粒直径；Re*为气相与液相的相对雷诺数.

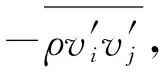
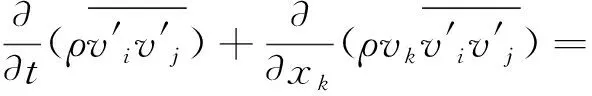
(6)

式中：xk为空间坐标；DT,ij为湍动耗散项,通过文献[12]简化的标量方程描述；φij为压力应变项，通过文献[13]提出的二阶压力-应变模型描述；Gij为浮力项；εij为耗散张量.可参照文献[14]进行建模，文中不再赘述.

1.2 网格划分与边界条件

在流域模型的空间离散化中，文中采用扭曲度较低的六面体网格对局部高点的管路模型进行离散.另外，为了更准确地模拟近壁面流动对湍流核心区的影响，以及边界层速度梯度的变化，在整个模型壁面设置10层边界层网格，近壁面网格Y+值为34.为了排除网格数量对计算结果的影响，准备网格数量为20.5万、35.9万、57.2万和119.7万的空间离散化方案，进行网格无关性检验，如图1所示，图中lv为垂向位置.

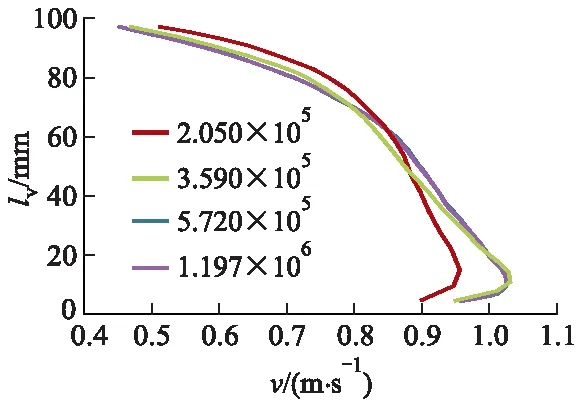
图1 网格无关性检验Fig.1 Grid independence test

给出了不同网格数量条件下，位于局部高点的管道截面流场速度分布情况.可以看出，当网格数量由57.2万增大至119.7万时，该截面的流速分布基本保持不变，最终确定流域模型的网格总数为57.2万.

在边界条件的设置中，管道入口边界使用UDF方法设置流速，使流速从0.2 m/s线性增加至0.8 m/s，流速变化过程总时长为0.5 s，气相体积分数为0.出口边界给定压力5 000 Pa，即水箱中的水位高度，气相无回流.管壁视为无滑移边界，壁面粗糙高度0.05 mm，粗糙系数0.5.由三维建模软件测量得到体积为300 mL气团在局部高点处静止时其液面所对应的坐标参数，使用Patch方法输入液面坐标参数及局部高点顶点的坐标参数，从而设置300 mL空气，气-液表面张力系数为0.07，接触角为50°.在求解方法的设置中，为准确预测每个时刻的气相运动，采用显式算法求解体积分数方程，时间差分采用一阶隐式格式.压力与速度耦合采用相耦合SIMPLE算法，所有对流项的差值均采用QUICK格式.对于TFM模型体系，其相间可以相互渗透，而实际中气团始终与水相存在明显边界.为此，引入VOF模型关于气液边界的定义，即边界位于气、液相体积分数均不为0的控制体内(网格)；在确定目标控制体后，通过Geo-Restruction(几何重构)差值算法最终确定气液交界面的形态.

2 试 验

2.1 试验装置

整个试验装置包括2个部分：循环管路系统和PIV测试系统如图2所示.循环管路系统的管径规格为DN100，由水箱、离心泵、电磁流量计、调节阀、压力传感器和测试件构成.水箱尺寸为1.2 m×1.2 m×1.2 m，离心泵额定流量为35 m3/h，电磁流量计测量精度小于0.3%，量程为0～80 m3/h.测试件(局部高点)采用有机玻璃制作,管径规格与系统管道同为DN100.为降低折射现象对图像采集的影响，测试件外壁为光滑平面；局部高点前后管路的倾角均为20°，距离水平管道的垂直高度为50 cm；上升管段布置有注气孔，通过向管内注气形成滞流气团.PIV测试系统由CCD相机、控制主机、同步器和激光器组成；其中，CCD相机采样频率为15 Hz，单张像素400万，距离测试件50 cm；激光器输出能量380 mJ，脉冲激光波长532 nm，通过透镜组聚焦后，可形成一个30°展角、厚度0.5 mm的片光.

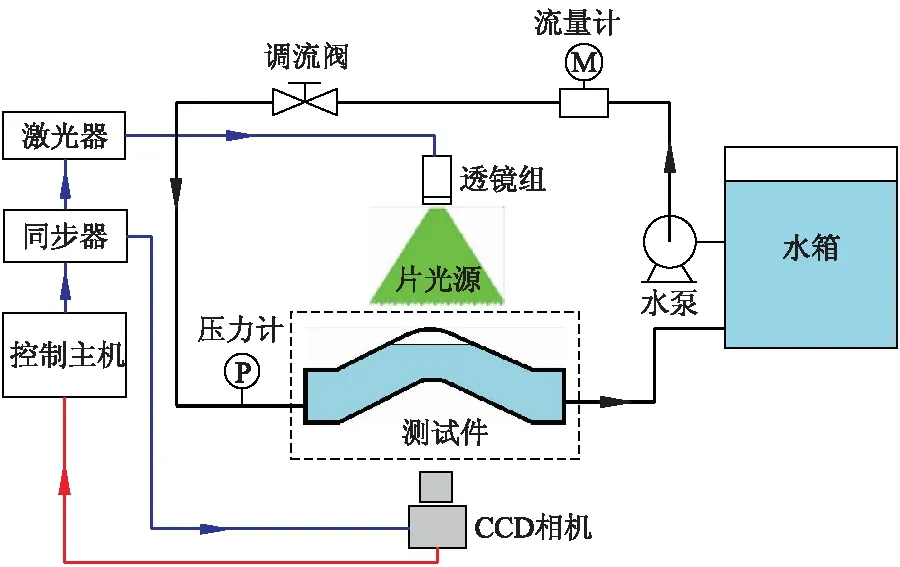
图2 滞留气团局部流场测试系统Fig.2 Test system for local flow field of entrapped air pocket

2.2 试验方法

本课题曾针对滞流气团在局部高点处的动力学影响因素进行了试验研究，结果表明，当管道流速在0.2 m/s以下时，气团保持静止，随着流速增大，气液交界面开始明显波动；当流速达到0.5 m/s时，流场的湍动和剪切作用逐渐使气团破碎，在气团尾端持续形成大量的小气泡；当流速达到0.8 m/s时，水流的冲击开始推动气团整体移动；为了观测局部高点处滞流气团的整体运动特性，循环管路系统的流速应达到0.8 m/s.试验开始前，向管内注入空气300 mL，在局部高点处形成滞流气团，随后整个管路系统先以0.2 m/s的流速运行.采用空心玻璃球作为PIV示踪粒子，密度1.06×103kg/m3，粒径大小70 μm，粒子浓度控制在16个/cm2左右.为了避免脉冲激光经过气液交界面后发生散射，将透镜组布置在局部高点底部50 cm处，即激光从测试件底部射入流场.在PIV测试程序中，将CCD相机跨帧时间设置为500 ns，脉冲激光射入流场时，迅速将调流阀调节到0.8 m/s流速所对应的开度，持续采集图像5 s.试验结束后，通过Insight 4G软件分析每组图像中示踪粒子的位移情况，进一步得出流场的速度分布.

3 试验结果与讨论

3.1 气团运动特性

图3为0.5～2.0 s各时刻，滞流气团运动特性的试验结果和流场模拟结果对比.从试验结果可以看出，当水流冲击滞流气团时，气团沿管壁整体呈楔形向下移动，速度逐渐增大.滞流气团前端的气液边界波动明显，该区域流场的剧烈湍动导致气团的表面张力无法维持其自身形态，进一步造成气团破碎并生成一定数量的小气泡；随着运动时间推移，气团前端的小气泡数量先逐渐增加然后趋于稳定，这是由于气团的破碎与小气泡的聚合效应达到了动态平衡.根据以上结果可知，滞流气团的下倾流动包括3个主要特征：① 气团整体向下移动；② 局部破碎成小气泡；③ 小气泡破碎与聚合动态平衡.

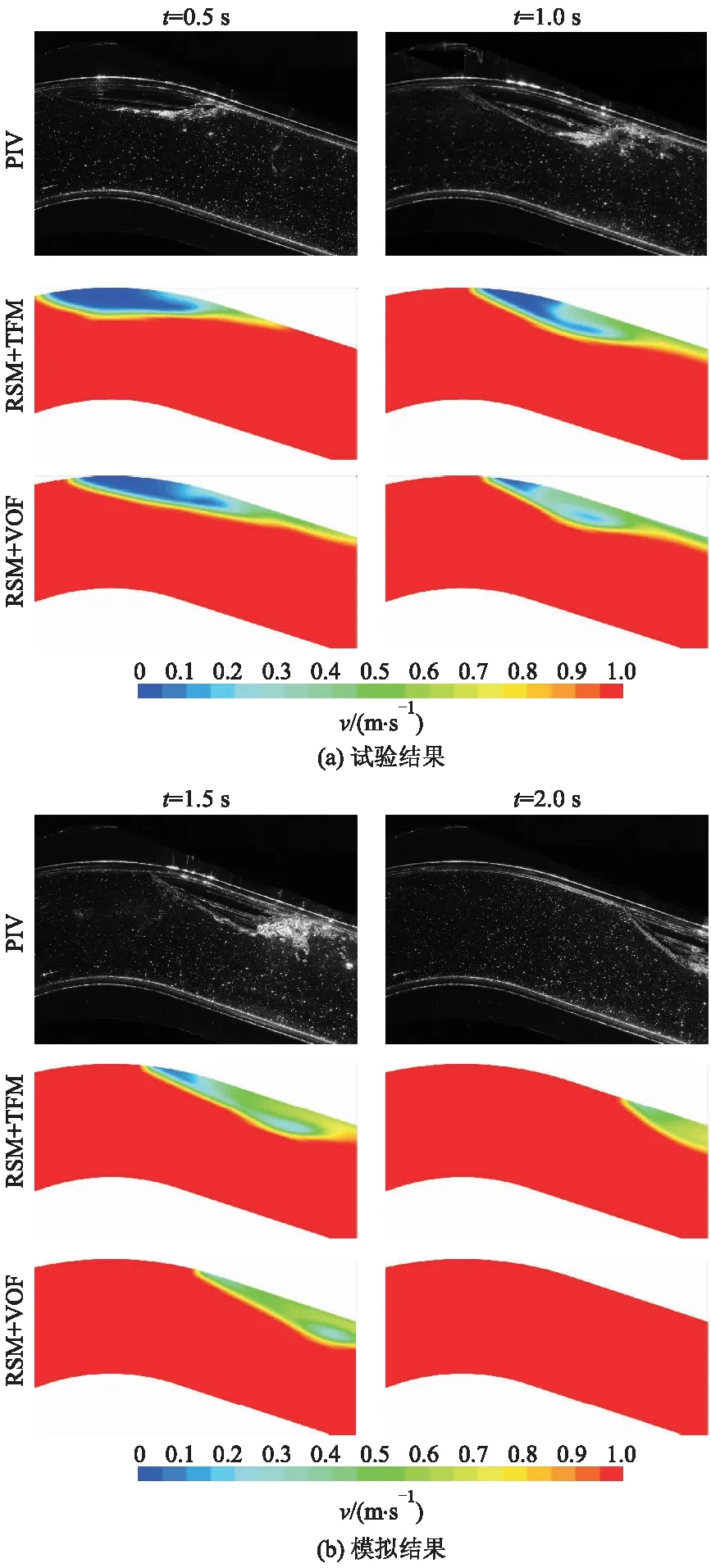
图3 气相运动试验结果与预测结果对比Fig.3 Comparison of PIV measured results and predicted results of gas phase motion

从流场模拟的结果可以看出，在不同时刻下，基于TFM模型得到的气团形态及空间分布与试验结果基本吻合，该模型能够准确预测滞流气团的整体运动特性.而对于气泡的破碎和聚合现象，该模型并不能模拟这一动态的过程，预测结果只显示出滞流气团出现局部的气液相混合.在基于VOF模型的流场模拟中，滞流气团的运动速度明显高于试验结果，这是由于VOF模型中水流和气团的运动只基于混合相的动量守恒方程求解，相间不存在动量交换和相对速度；而实际情况中，气团的运动是由于水流冲击和拖拽产生动量传递，两者之间必然存在明显的速度滑差，因此通过VOF模型模拟滞流气团的运动并不准确.

图4为流场出口截面的气相体积分数θv变化曲线.根据曲线的时间跨度可得出，VOF和TFM模型的预测结果中，气团通过出口的时均流量分别为375 和263 mL/s，这与图3所示的结果相符.另一方面，对于VOF模型预测的气相体积分数曲线，其上升和下降时的梯度均处于较高水平，侧面反映出气团通过出口时的空间分布较为集中；而在实际情况中，滞流气团前端的小气泡群率先通过出口，气相体积分数应该缓慢提高，当气团到达并通过出口时，气相体积分数急剧升高后骤降；因此，TFM模型的预测结果与实际更为接近.图5为气团纵截面平均压力随时间的变化情况，在气团的下行过程中，其压力在1.0～9.0 kPa振荡，振幅逐渐衰减，最终稳定在4.8 kPa；由于TFM模型附加了动量传递对气相体积变化的影响，其预测结果中压力脉动的衰减速度要大于VOF模型.

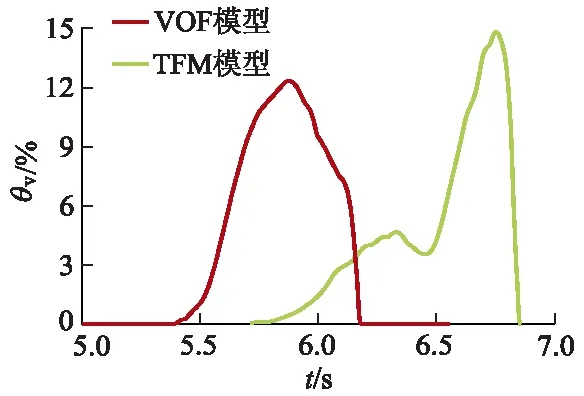
图4 出口截面气相体积分数变化对比Fig.4 Comparison of gas phase volume fraction change at outlet section

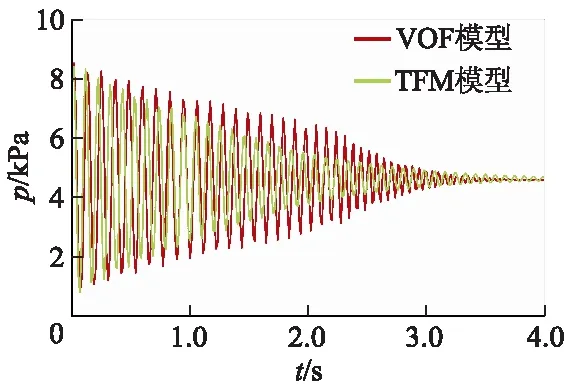
图5 气团纵截面平均压力变化结果Fig.5 Result of entrapped air pocket average pressure change on vertical section

3.2 流场速度

图6为滞流气团局部流场速度分布的PIV测量结果和数值模拟结果对比.

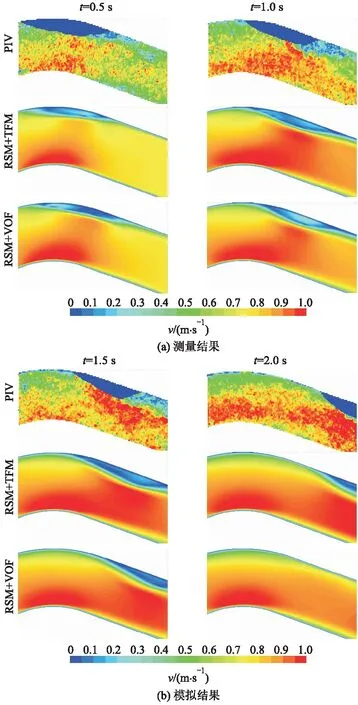
图6 流场速度PIV测量结果与预测结果对比Fig.6 Comparison of PIV measured results and predicted results of flow velocity

实测结果显示，滞流气团所在的区域通流截面积减小，因此气团下方的水流速度较高，尤其在气团的迎流面附近，流速可达到整个流场的最高水平(1.0 m/s以上).另一方面，气团相对于水流运动速度较低，对来流的阻碍作用显著，这导致气团背流面会出现1个流动死区，流速明显低于流场其他区域(0.2 m/s以下).从以上流速分布特性可以看出，气团前端是整个流场中速度梯度最大的区域，在较强的剪切力作用下，该区域必然会产生尺度较大的涡流，这是导致气团局部流场紊乱和破碎直接原因.通过对比数值模拟结果发现，TFM模型预测出的流场时均速度变化与实测结果基本吻合，总体上可以实现流场的定量分析.而对于VOF模型，由于不能准确模拟气团运动行为，其对流场速度分布的预测结果与实际情况还存在明显差异.

4 结 论

1) 相对于VOF模型忽视相间动量交换和相对运动，导致预测出的气团运动速度大于实际情况，而TFM模型考虑了动量传递引起的各相运动状态变化，且各相独立的动量方程可以模拟相间的相对运动.

2) 在滞流气团的下倾运动中，其前端是流场中速度梯度最大的区域，流体在剪切力的作用下会形成明显的涡流，直接导致该区域流态紊乱，当气团表面张力无法克服流场湍动并维持其自身形态时，气团局部开始破碎并形成小气泡群.

3) 对于滞流气团前端的气泡破碎再聚合现象，TFM模型和VOF模型均无法准确模拟这一过程.