有压平直管道内交汇柱系下游流场特性分析

鲁一凡，李永业，赵一名，宋晓腾，强懿鹏，原源，陈润

(太原理工大学水利科学与工程学院, 山西 太原 030024)

筒装料管道水力输送是一种新型在研的管道水力输送技术，其原理在于通过水流推动管道车在管道内运动来实现运输物料的目的，因其节能环保且稳定性较高，具有较为广阔的应用前景.管道车由封闭的圆柱壳体料筒和两端圆柱状支撑体组成，由于在管道流场内具有复杂几何结构的交汇式柱系的存在，会在管道车下游形成涡旋[1]，并产生机械能的损耗，影响筒装料管道水力输送的整体能耗[2].因此，加强对交汇式柱系绕流尾迹流场特性的研究，分析其流场速度空间分布特性，可为优化筒装料管道输送能耗提供一定的理论指导和数据支持.

钝体绕流问题存在较为广泛[3]，国内外学者已经针对钝体绕流进行了大量的研究工作.樊晓羽等[4]使用粒子图像测速仪(PIV)结合数值模拟，研究了在Re=3.42×104时，不同间隙比串列双方柱在干扰效应下的流场结构，指出间隙比为4时串列双方柱流场出现双稳态现象.杜晓庆等[5]采用大涡模拟的方法，研究了在Re=1.40×105时，并列双圆柱流场特性随间距比的变化规律，研究表明绕流场的流态结构随并列圆柱间距的增大会呈现从单一钝体、偏向流到平行涡街的变化.邱玥[6]基于PIV技术，研究了正三棱柱体在低雷诺数下的流动特性，得出Re在200～1 500时，尾涡形成长度随雷诺数的增加呈先增加后减少的趋势，并在Re=800时达到最大值.YOON等[7]对波状圆柱的绕流场进行了数值研究，表明波状圆柱在具有稳定的涡激抑制功能，能够显著抑制圆柱升力.林海花等[8]采用RNGk-ε模型对复杂齿条弦杆的绕流流场进行了分析，研究表明弦杆与来流速度矢量夹角θ与拖曳力系数Cd呈正相关，当θ<30°时，Cd随θ增加的速度较为缓慢，夹角大于30°时，增加速度显著提高，在90°时达到最大.姚世传等[9]采用大涡模拟对倒圆角方柱的非定常流动特性行了二维和三维的模拟研究.JOODAKI等[10]研究了二维情况下Re=200时双分板在圆柱上下两侧对圆柱绕流的影响，指出平板夹角与阻力系数呈正相关，平板夹角增大可以减小涡脱落频率，提高柱后流动的持久性.MAGNIER等[11]采用PIV技术分析了海底并联双壁面障碍物的湍流性能，表明上游立方体的存在对下游圆柱的大尺度流动结构有明显抑制作用，进而影响圆柱绕流尾迹的发展.ASIM等[12-13]基于DPM模型系统研究了简单几何形状囊体在弯管内运动时的流场特性和压力分布特性.MIYANAWALA等[14]对圆柱尾迹进行了线性分解，得到了圆柱尾迹的降阶模型.

综上，目前国内外学者已经对不同形式的钝体绕流进行了大量研究，但钝体本身的几何结构较为简单，针对绕交汇式柱系结构产生的绕流现象研究较少.因此，文中通过采用LES方法对单个交汇式柱系静止状态下的绕流场速度特性进行研究.

1 模型建立

1.1 控制方程

文中采用LES-WALE模型对静止柱系在有压有限域内的绕流进行模拟，过滤器选用盒式过滤器，过滤后的N-S方程中连续性方程为

(1)

动量方程为

(2)

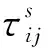
1.2 几何模型构建

几何模型的边界由管道车简化的交汇式柱系与平直管道2部分组成.交汇式柱系主要有料筒主圆柱和料筒两端的支撑体类圆柱连接组成.两端各有3个支撑体，并关于料筒轴线呈120°旋转对称安装.主圆柱长L=100 mm，直径D=70 mm，管道长度为Lpipe=2 200 mm，管道内径Dpipe=100 mm.图1为管道车模型示意图.

图1 模型示意图Fig.1 Schematic diagram of model

1.3 网格划分

在柱系周围的流体域采用四面体网格，柱系上下游采用六面体O型网格 ，并在2种网格的交界面上进行网格的组合(见图1b).采用2，3，4，5 mm共4种网格进行网格无关性检验，当网格尺度为3 mm时，轴向流速最大相对误差为3.82%，当网格尺度为4 mm时误差为2.45%，当网格尺度为2 mm时误差为2.08%.可见当网格尺度在2 mm时相对误差已经不大，综合考虑了计算结果和计算时间，最终选取了全域网格最大尺寸为2 mm，并对交汇式柱系周围网格加密后进行计算.

1.4 边界条件及求解器设置

入口边界采用速度入口、出口边界为压力出口，管道壁面和柱系壁面采用无滑移边界.速度入口条件根据来流流量计算并给定实测管道流场速度分布，选取流量为20 m3/h，管道流场特征长度Dpipe=100 mm、特征速度U=0.707 m3/h.压力出口采用自由出流p=0 Pa.采用SIMPLE算法进行速度-压力耦合计算，各项收敛精度为1.0×10-6.考虑到网格变形对流场求解精度的影响，故柱系的运动采用Moving Wall方式实现：采用试验中实测的运动速度(0.534 m/s)作为边界条件输入.压强项的离散格式采用二阶格式；动量项的离散格式采用有界中心差分.

1.5 特征面选取

由于交汇式柱系结构关于料筒中轴线(即管道中轴线)呈120°旋转对称，所以特征面的选取从管道中轴线来流方向(记为Z轴正方向)和垂直于中轴线的平面(记为XOY面)2个方面考虑.在Z轴方向设置过管道中轴线的铅垂面和水平面2个特征面，分别记为断面1和断面2，如图1c所示.在平面XOY中，将料筒下游端底面记为Z0，顺水流方向在柱系下游设置6个断面，如图1d所示，依次记为Z1，Z2，Z3，Z4，Z5，Z6，其中Z0到Z2为下游近端横断面，Z3到Z6为下游远端横断面，各特征断面与Z0的距离l如表1所示.

表1 特征断面位置Tab.1 Position of characteristic section

2 模型验证

物理试验系统如图2所示，主要由动力系统、调节系统和测试系统3个部分构成.动力系统为离心泵，调节系统由电磁流量计和闸阀组成、测试系统包括测试段管路和多普勒激光测速仪(LDV)等.系统管道全长24.7 m，由内径为100 mm的透明有机玻璃管道组合而成.测点位于断面Z1与断面1的交线上，所测流速为管道的轴向流速，具体测点坐标如表2所示.

图2 试验系统示意图Fig.2 Schematic diagram of test system

表2 测点位置Tab.2 Position of measuring points mm

使用LDV连续多次测量测点轴向流速，并对LDV所测得的数据进行时均化处理并采用多次试验的平均值，LDV的速度测量精度为95%；数值模拟数据同样采用时间平均的处理方式，将试验所测得的数据与模拟对应位置数据相对比，数值模拟数据和试验数据吻合度较高，经计算最大相对误差不超过8%，证明了模拟数据的准确性.

3 试验结果分析

3.1 纵断面速度特性

图3a为断面1与断面2的速度分布.由图3可知，在柱系下游的尾部区域内速度分布不均匀程度较大，存在着低速流区和高速流区.其中低速区主要集中在交汇柱系的主圆柱体后端面附近位置，交汇柱系与管壁之间的环隙区域向近端下游的射流形成了尾部区域速度场中的高速区.通过比对断面1与断面2可以发现，断面2中高速区特征尺度与耗散位置较为相近，这是由于在该断面内边界条件高度对称所导致的；而断面1环隙末端，支脚下游附近的流速较小并未形成高速区，无支脚存在的环隙末端出口高速区形成较为明显；断面1内的流速分布不具有对称特点，其速度场总是以无支脚存在的环隙后方高速区为主导，并且该高速区除了沿流向发展的长度尺度明显大于断面2中的对称高速区流向长度，在展向发展的长度尺度也同样较大；断面1中这种不对称的高速区出现，总体上原因在于交汇式柱系的复杂边界条件在该断面内的不对称特点.

图3 断面1,2速度及流线图Fig.3 Contour and streamline of section 1 and 2

图3b为断面1和断面2上的瞬时流线图.由图3可知，流线从环隙出口进入下游流场时，部分流线急剧弯曲汇集在交汇柱系主圆柱体后方，部分流线并未弯曲或并未发生明显弯曲，继续沿流动方向延伸到远端下游.在交汇柱系主圆柱体后方的急剧弯曲流线形成了明显的涡旋，其中断面1内的涡旋较为细碎，特征尺度较小，而断面2内的涡旋相比断面1内的涡旋特征尺度较大；两者涡旋特征尺度明显区别的原因在于：断面2内边界条件高度对称，两侧高速流区互相作用、交替占据主导地位、不稳定性较强，从而下游涡旋交替产生，类似于经典圆柱绕流现象在交汇柱系下游产生主圆柱体特征尺度的涡旋；断面1内边界条件不对称，高速流区始终占据主导，流场较为稳定，较小涡旋无法通过流动失稳而发展为较大涡旋.

3.2 近端横断面速度特性

图4为断面Z1,Z2的流速分布示意图，交汇柱系下游近端区域内的高速流区与低速流区明显以主圆柱体在横断面内的投影为界，内部的低速流区近似一圆面，并且在3个支脚圆柱处低速流区向高速流区略有侵入；而高速流区近似一圆环，并对低速流区的侵入有所响应，在支脚圆柱处高速流区并不连续且在支脚处的速度梯度明显较大.从断面Z1沿流向到断面Z2，低速流区域尺度与形状并未发生明显变化，但是由于断面Z2内支脚圆柱体的存在，流速在支脚处有所增大.

图4 断面Z1，Z2流速及流线图Fig.4 Contour and streamline of section Z1 and Z2

在交汇柱系后的涡旋实际上是三维涡旋，该三维涡旋在横断面内的投影以图4为断面Z1,Z2上的流线图表示.交汇柱系近端下游沿流程从断面Z1到断面Z2由于支脚圆柱体的出现引起边界条件的变化，故涡旋的尺度与强度都有所上升：三维涡旋在横断面内同一投影位置处，从断面Z1到断面Z2，相应位置处的涡旋处流线更加密集，表征其速度梯度剧增、涡旋强度同样增大；并且原本在断面Z1内流线较为平滑未形成涡旋处，在断面Z2相应位置处流线急剧弯曲、缠绕，形成了新的涡旋.

3.3 远端横断面速度特性

图5a为断面Z3—Z6的流速分布图.

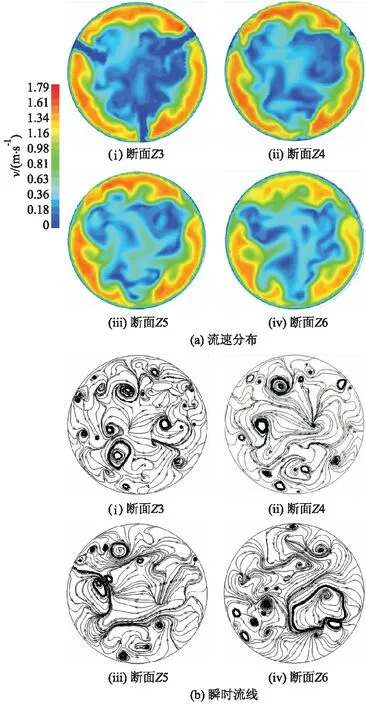
图5 断面Z3-Z6流速及流线图Fig.5 Contour and streamline of section Z3 to Z6

交汇柱系下游区域，其高速流区范围总体上有着沿流程增大的趋势，但是其幅值沿流程逐渐减小；低速流区范围总体上沿流程逐渐缩小，但是其幅值总体沿流程增大；低速流区与高速流区的速度差值沿流程逐渐减小.高速流区范围扩大伴随着低速流区范围缩小；根据流动的能量机制，高速流区向低速流区传递动量时其自身动能损耗，低速流区获得动量并且其动能提高，故低速流区速度幅值沿程增大、高速流区速度幅值沿程降低，最终2种流区的速度趋近于相同并恢复管道中的高雷诺数湍流流速分布.

图5b为断面Z3—Z6上的流线图.交汇式柱系后的一些三维涡旋在断面Z3到Z6上的投影位置相同，另一些三维涡旋投影位置发生了变化，这是由于这些三维涡旋在横断面内的展向运动所致.从断面Z3沿流程到断面Z6，涡旋的数量略有下降，并伴随着涡旋的强度增大，这说明一些较为细碎的涡旋沿流程有着归并的趋势，归并后的涡旋尺度相对较大.

3.4 流场沿程压强变化

图6为交汇柱系下游流场的沿程断面平均压强变化，原本较为平缓降低的管道压强，由于交汇式柱系的存在能够在一定程度上造成压强的剧烈变化.由于环隙出口(下游流场入口)初始速度较大，断面Z1上的压强值大于同一流量下管道流场压强值27%，这一趋势持续到断面Z2—Z3间发生改变.从断面Z3之后，管道流场压强始终大于柱体下游流场，这是由于交汇柱系存在所引起的压强(势能)损失，在断面Z6上，管道流场与交汇柱系流场的压强差距已经不大，仅为3.4%.

图6 沿程压强变化Fig.6 Pressure variation along section

4 结 论

1) 有压管道内，交汇柱系下游流场的速度场整体上可分为低速流区与高速流区2部分：其中靠近管壁的环隙下游区域(除支脚附近区域)为高速流区，在横断面上表现为近似圆环状的高速条带，并且该高速流环在纵断面内沿流程先增大再减小；靠近管道核心的柱系下游区域为低速流区.由于交汇柱系的主圆柱体与管道壁面共同构成的边界具有旋转对称性，因此，在横断面内，高速流区近似圆环，低流速区近似圆面；并且由于支脚圆柱体存在，高速流区与低速流区在原有近似圆形基础上分别有着凸角与凹角.

2) 交汇柱系下游，高速流区流线沿流程向远端延伸，而低速流区的流线急剧弯曲形成了三维涡旋，并且这些三维涡旋有着不同程度的展向运动与归并、缠绕现象.流场纵断面内，边界条件高度对称时涡旋的尺度要大于边界不对称时的涡旋尺度；流场横断面内，交汇柱系近端涡旋较多、有些较为细碎，而这些细碎的涡旋有着归并与缠绕导致远端涡旋较少，涡旋尺度较大.