一种改进的液压伺服预测控制系统

戴永彬

(辽宁工业大学软件学院，辽宁锦州 121000)

0 前言

液压伺服系统由于具有响应快、位置跟踪准确等优点，被广泛应用到工业生产的各个领域中。但是液压伺服系统具有较强的非线性、时滞等特点，因此众多学者提出了多种控制策略，获得了较好的控制效果[1-3]。其中，预测控制是一种比较有效的控制方法。文献[4]针对液压伺服系统时变、模型不确定性等问题，采用预测函数控制算法设计了液压振动伺服控制器，实验结果表明该控制器具有较强的鲁棒性和抗扰能力。文献[5]利用多目标粒子群算法实现了非线性预测控制算法的滚动优化，并应用到液压伺服系统中，其算法负担小、实时性好。文献[6]设计了一种基于混合模型的液压伺服控制器，外环采用传统模型预测控制算法，内环采用改进的PID控制，实验结果表明其跟踪精度高、波动小。文献[7]将模型预测控制算法和卡尔曼滤波以及二次优化算法相结合，设计了一种综合控制器，提高重载机械手旋转驱动系统的位置控制精度。

常规的非线性预测控制实质上是一种单目标优化的算法。只要保证目标函数最小即可，但是不能保证目标函数中每一项预测误差同时最小，为此采用多目标非线性预测控制算法可以提高算法的预测精度[8]。目前，非线性预测控制的求解主要采用多目标粒子群算法，但多目标粒子群在快速收敛时，很难兼顾种群粒子的多样性[9-12]。为此，本文作者采用类圆映射[13]，将高维目标空间的粒子映射到类圆二维平面并利用差熵指标监控种群进化的状态。在种群进化的不同阶段选择相应的全局最优粒子，利用新的种群距离公式和面积支配管理外部档案集。将改进算法应用于液压伺服系统。

1 QCMPSO算法的改进

1.1 种群进化状态的监测机制

多目标进化算法在种群进化过程中需要经过探索、发掘或停滞等过程。当确定高维算法的进化状态比较困难时，将高维目标空间映射到二维平面是一个比较有效的方法。文中利用类圆映射将Pareto前沿映射到类圆二维平面，使用差熵指标来监控种群的变化。

1.1.1 类圆映射原理

类圆是平行坐标映射中的一种方法[13]。类圆映射示意如图1所示，该映射能避免数据遮挡并且保持原高维多目标空间Pareto前沿形状、位置关系以及支配关系，适用于高维目标的种群状态监控。

图1 类圆映射Fig.1 Quasi-circular mapping

映射过程如下：

首先，将待解集进行规一化。公式如下：

(1)

其次，将多目标均匀分布在单位圆C0圆周上，坐标Vλ(i)公式如下：

(2)

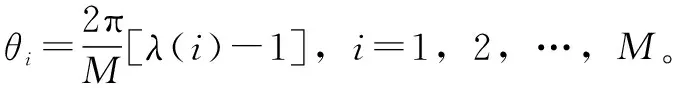
最后，把归一化后的解集个体映射到单位圆圆心o和Vλ(i)的连线上，且映射点到o的距离为

(3)

1.1.2 类圆扇块的划分

对于进入档案集的非支配解，可映射到类圆平面的扇区中，形成由若干同心圆和射线围成的扇块，具体如图2中的虚线区域，其扇块数为K×M个。类圆扇块标号为

(4)

这样就将一个多维粒子作为一个向量映射到到类圆平面内，每个粒子的某个分量都位于一个扇块内。

图2 在类圆平面上划分扇块Fig.2 Sectors on quasi-circular flat

1.1.3 基于类圆的差熵

为了掌握种群进化的情况，文中采用熵和差熵作为指标衡量Pareto前沿的状态，从而估计种群进化所处的阶段[10]。具体公式如下：

(5)

ΔE=E(t)-E(t-1)

(6)

其中:nkm(t)表示落在第k行第m列扇块内的坐标分量的数量。

种群一般具有3种进化状态，如收敛、多样化和停滞的状态，可以使用2个阈值进行判断，阈值公式如下：

(7)

(8)

其中：当前档案集A的规模为Q。

为了判断种群进化不同的阶段，可以使用上式的阈值公式，具体判定过程如下：

(1) 当|ΔE|>α或A(t)≠A(t-1)，种群处于收敛状态；

(2) 当A=K且β<|ΔE|<α，种群处于多样化状态；

(3) 当A=K且|ΔE|<β，种群处于停滞状态。

1.2 档案集的维护和全局最优粒子的选择

按照多目标粒子群的优化原理，档案集维护和全局最优粒子的选取对种群寻优能力和解集的性能有着至关重要的影响。为了保证解集的收敛性和多样性，文中根据种群进化状态自适应调整档案集的维护和全局最优粒子的选择策略。

1.2.1 收敛度指标

为了评估种群的收敛程度，文中采用类圆支配的概念作为收敛程度的指标。类圆支配的概念描述如下：

映射粒子各维的目标函数值构成一个多边形(如图1中的虚线构成的图形)，其面积越小，相对其他面积大的粒子占优，因此可以利用粒子映射面积的大小衡量种群粒子的收敛情况。

1.2.2 扇块距离

文中通过计算种群粒子每一维类圆扇区块数量的差值，估计粒子的分布性。值越小说明分布性越好。具体公式如下：

(9)

(10)

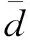
1.2.3 档案集的维护

目前大部分档案集维护算法不考虑种群的进化状态而采用固定的策略进行管理。文中根据种群进化状态，自适应选择管理策略，对档案集多余粒子进行剪裁。首先，对粒子映射面积S和扇块距离Di升序分别排序。其次，当种群处于收敛状态时，按照S、Di次序依次排列粒子；当种群处于多样性状态时，按照Di、S次序依次排列粒子。排序后，根据档案集规模删除排序靠后的多余粒子。

1.2.4 全局最优粒子的选择

为了更加准确地选择全局最优粒子，在种群进化的不同阶段选取不同性质的最优粒子。具体公式如下：

gBest(t+1=

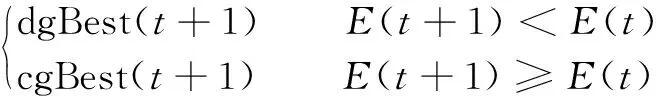
(11)

其中：gBest(t+1)为全局最优粒子；dgBest(t+1)为提升多样性的全局最优粒子；cgBest(t+1)为改善收敛能力的全局最优粒子。

对于cgBest(t+1)，可按照公式(12)选择：

cgBest(t+1)=argmin(Di)

(12)

对于dgBest(t+1)，可按照公式(13)选择：

dgBest(t+1)=argmin(Si)

(13)

1.3 改进算法的验证与分析

选用ZDT和DTLZ系列中典型函数进行测试。对比算法为NSGA2[14]、SPEA2[15]、MPSO-D[16]，并分别对2～5个目标检测算法的性能。MATLAB仿真参数设置：种群和档案集的规模设置为100，最大迭代数为1 000，进化算法的变异和交叉的概率分别为0.9、0.1。其他仿真参数详见文献[14-16]，仿真结果如表1和表2所示。

表1 对比算法的仿真图Tab.1 Simulation charts of comparing methods

表2 测试结果Tab.2 Test result

(1)评价方法

文中采用世代距离(Generational Distance, GD)、分散性指标(Spread, SP)分别检验对比算法所获解集的收敛性和多样性，2个指标值越小说明性能越好。

(2) 验证与分析

通过仿真可知，ZDT函数测试的结果较为接近，都能靠近Pareto曲线且粒子分布比较均匀。这是由于在二维平面上粒子之间的支配关系清晰，计算负担较小。文中算法和SPEA2表现较为优异。DTLZ函数主要测试了算法的多目标情况，文中算法在分布性和收敛性上表现最优， SPEA2 分布性较好，主要是因为采用了密度指标衡量粒子的多样性，在高维空间比较有效。

2 基于QCMPSO-NPC液压伺服系统

2.1 液压伺服系统的模型

液压控伺服系统的状态方程[17]为

(14)

y=[0 0 1]x

(15)

式中：m为负载质量；Ap为液压缸工作面积；Cp为活塞和负载的黏性阻尼系数；K为负载弹性刚度；Ct为液压缸的泄漏系数；Bt为液压缸的阻尼比；Kv为功率放大器或伺服阀系数；F为系统干扰；其他参数详见文献[17]。

将上述模型处理后，针对广义预测控制算法(GPC)、PSO-NPC算法和QCMPSO-NPC算法分别设计液压伺服系统控制器，追踪幅值为1的方波信号。主要仿真参数设置为：m=150 kg，Bt=0.081×10-11，Ap=0.012 m2，Kv=0.001，Ct=2.6×10-10，K=72；粒子种群和档案集规模为50，c1=c2=2，w=0.5，优化迭代次数设为100，预测时域步数为5，控制域步数为3。

2.2 液压伺服系统的仿真与分析

文中利用多属性决策方法进行决策，选择非劣解集中的最优解[18]。仿真结果如图3—图5所示。

图3 广义预测的位置输出(a)及误差(b)Fig.3 Output(a) and errors(b) of GPC

图4 常规PSO-NPC位置输出(a)和误差(b)Fig.4 Output(a) and errors(b) of conventional PSO-NPC

由图3可知：GPC的输出在初始阶段震荡剧烈，位置最追踪误差较大，在运行1或2个周期后趋于稳定，其算法的稳定性和准确性比较差。GPC虽然可以克服模型失配、时滞等问题，但是需要对液压伺服系统模型线性化，由此产生的误差较大，无法实现精确控制。由图4可知：PSO-NPC算法控制效果优于GPC算法，主要表现为超调较小、响应快、位置追踪准确，但是输出曲线会偶发震动，误差曲线随之波动。这是由于PSO-NPC算法是一种单目标优化算法，不能保证预测误差都为最小，因此会造成输出曲线偶发波动。文中提出的QCMPSO-NPC算法保证了解集的收敛性和多样性，因此输出响应最快，误差最小，位置跟踪性能优于以上2种算法，如图5所示。

图5 QCMPSO-NPC位置输出(a)和误差(b)Fig.5 Output(a) and errors(b) of QCMPSO-NPC

实际上，对于PSO-NPC算法，提高仿真迭代次数或粒子种群规模也可以提高液压伺服系统的输出性能。如将仿真迭代次数提高到200次后，系统输出曲线已接近设定曲线，误差较小。但提高迭代次数或种群规模会使系统的计算负担成几何级数增加，严重影响系统响应的实时性。

综上所述，文中提出QCMPSO-NPC算法具有较高的控制精度，适合于液压伺服系统的控制。

3 结论

为了解决液压伺服系统时滞、非线性等问题，文中将基于粒子群优化的非线性预测控制进行改进并设计了液压伺服系统控制器。为此，文中采用类圆映射技术将高维目标映射为二维类圆平面，监控种群进化情况并自适应选择全局最优粒子和档案集管理策略，兼顾了解集的收敛性和分布性。通过仿真实验，验证了基于QCMPSO-NPC算法液压伺服控制系统的有效性和可行性。