事件触发脉冲控制多智能体系统的安全一致

高安安，胡爱花，江正仙

（江南大学 理学院，江苏 无锡 214122）

0 引言

随着通信网络技术的发展，多智能体系统越来越受到重视，并广泛应用于同步控制［1-3］、机器人协同［4］、传感器网络［5-6］、无人机编队［7］控制等方面，其中，一致性问题是多智能体系统研究的热点问题，也是根本性问题。

在一致性问题中，多智能体系统的安全一致性问题成为关注重点。简单来说，安全一致性指存在网络攻击时，多智能体系统的一致性情况。由于网络攻击对网络的一致性具有破坏性的影响，因此，研究具有网络攻击的多智能体一致性问题变得至关重要。常见的网络攻击有：拒绝服务（Denial of Service，DoS）、窃取、骚扰、欺骗等。目前对于网络攻击下的一致性问题已取得了一些成果，如：文献［8］研究了存在DoS 攻击和输入饱和下的领导-跟随者网络的安全一致性问题；文献［9］研究了DoS 攻击下基于采样控制的多智能体一致性；文献［10］则研究了双层网络结构下存在DoS 攻击的安全一致性。

值得指出的是，不同于上述文献［8-10］中一致性误差系统渐近收敛到零，在安全一致性相关研究中，有些文献实现了一致性误差系统的均方有界收敛，如：采用脉冲控制方法，文献［11］研究了欺骗攻击下多智能体的均方有界一致性问题；文献［12］考虑了带有随机噪声的智能体状态方程，得到了欺骗攻击下多智能体系统均方有界一致的充分条件；文献［13］在系统存在时延和噪声的条件下，设计了一种状态估计器，实现了多智能体状态估计误差的均方有界一致。相较于DoS 攻击，欺骗攻击形式更为复杂［11-12］，通过注入虚假信息到控制器，对系统一致性造成了破坏性影响，同时难以被检测和识别。因此，本文考虑网络中存在欺骗攻击的非线性多智能体系统，进一步研究均方有界一致性问题。

在多智能体一致性研究中，现有文献中采用了多种控制方法，包括采样控制、间歇控制、牵引控制、事件触发控制和脉冲控制等。如文献［14］研究了牵引控制下多智能体的一致性问题；文献［15-16］使用事件触发控制方法，得到了多智能体系统的一致性。多智能体安全一致性研究中，这些控制方法也被加以使用，如：文献［17-18］研究了基于事件触发控制的多智能体安全一致性；文献［19］考虑了时延情况下多智能体安全一致性问题。另外，针对一致性问题，单一控制方法往往无法获得良好的一致性效果，因此多种控制方法的组合也被广泛应用于多智能体一致性问题的研究，在一致性收敛速度和控制成本方面有较好的改善。脉冲控制方法仅在离散时刻点施加控制，经济有效。但传统脉冲控制周期固定，本文结合事件触发机制，提出分布式事件触发脉冲控制方法，深入研究多智能体系统的安全一致性。由于脉冲控制对于脉冲间隔有严格要求，因此事件触发条件的设计具有挑战性。

基于上述讨论，针对欺骗攻击下多智能体系统的安全一致性，本文在固定脉冲时间间隔控制［11］的基础上，进一步结合事件触发机制［18］，得到了领导-跟随者多智能体系统在事件触发脉冲控制下的安全一致性。最后，通过数值仿真验证了理论结果的有效性。

本文提出了一种具有触发时间间隔上界的事件触发脉冲控制方案：当控制器的触发时间间隔达到给定的时间上界，即使事件触发条件没有满足，也会进行触发，产生脉冲信号，同时更新触发条件；进一步，与单一固定脉冲时间间隔的脉冲控制方法相比，引入的事件触发机制能够加快一致性速度，灵活地控制脉冲时间间隔。

1 问题描述

1.1 预备知识

1.2 多智能体模型描述

考虑一个包含N个跟随者的领导-跟随者多智能体系统网络模型，领导-跟随者多智能体系统的网络模型描述如下：

在原有固定时间脉冲控制的基础上，为了能够优化调整脉冲时间间隔，引入事件触发机制。在本文中，事件触发时刻即是脉冲时刻，而事件触发时刻由事件触发条件控制。接下来，将会分析给出事件触发条件。

对于智能体i，先考虑脉冲时间间隔固定，设脉冲时间间隔为h，且h1＜h＜h2，即：

再设无最大触发时间间隔限制的事件触发条件为：

1.3 欺骗攻击模型描述

本节主要介绍脉冲控制器遭受欺骗攻击的情况。首先，给出系统遭受的攻击为ξi(t)，接着给出系统遭受攻击的概率，设随机变量θi(t)表示事件智能i在t时刻被攻击的结果：令θi(t)=1 表示攻击成功，θi(t)=0 表示攻击失败；并且P(θi(t)=1)=，P(θi(t)=0)=1-，其中∈[0，1]是一个常数。接下来，我们给出脉冲控制模型。如果欺骗攻击成功，则第i个智能体接收的脉冲信号将被错误的数据所取代；如果没有攻击或者攻击失败，则脉冲信号为式（2），即：

针对上述多智能体系统，为了便于理论分析，给出如下假设。

假设1 智能体网络存在以领导者为根节点的有向生成树。

假设2 对于非线性函数f(·)，存在非负常数rij(i=1，2，…，N，j=1，2，…，n)使得对于任意x1，x2∈Rn有下式成立：

假设3 随机变量θi(t)(i=1，2，…，N) 相互之间是独立的。

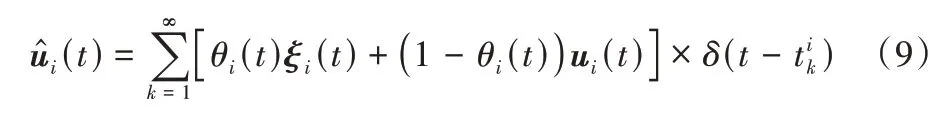
结合式（9），受到欺骗攻击的多智能体系统（1）可以进一步表示为：

定义1［11］如果存在一个闭集z和一个正常数σ，对任意的xi(0) ∈Rn，误差系统ζ(t)的数学期望（用符号表示则为E{‖ζ(t)‖}）收敛于集合z，则称多智能体（1）是均方有界一致的：

2 欺骗攻击下多智能体安全一致性分析

本节将给出遭受欺骗攻击的多智能体系统（1）在控制协议（9）下实现安全一致性的充分条件。

定理1在假设1 至假设4 成立的条件下，如果存在正定矩 阵P和正数α＞0，c＞0，ε＞0，φ∈(0，1)，μ=(1+ε)φ∈(0，1)使得下式成立：

则误差系统（12）实现了均方有界一致，且界限为z1，其中：

至此，误差系统实现了均方有界一致，这意味着多智能体系统（1）在控制协议（9）下实现了安全一致性。需要指出的是，事件触发机制可能导致芝诺行为的发生，从而破坏系统的稳定性。接下来，我们将排除芝诺行为。

3 数值仿真

本章将通过两个例子来验证理论结果的有效性：例1 是具有1 个领导者和4 个跟随者的多智能体系统；例2 则是网络拓扑结构中不存在以领导者为根节点的有向生成树的仿真事例。

例1：考虑一个具有4 个跟随者和1 个领导者的多智能体系统，领导者和跟随者的网络拓扑如图1 所示。

图1 例1的多智能体的网络拓扑图Fig.1 Multi-agent network topological graph of example 1

图1 中数字0 代表领导者智能体，数字1～4 代表跟随者智能体，则可以得到拉普拉斯矩阵为：

领导者与跟随者2 和跟随者3 有牵引关系，可以表示为D=diag{0，3，2，0}。

多智能体系统中领导者的运动方程为：

跟随者的运动方程满足：

因P(θi(t)=1)=，可取攻击发生概率θˉ=0.1；取攻击数据为ξi(t)=[0.11，-0.11]T，则有ξ=0.0242。为了便于分析，设定参数c=0.35，ε=0.2。用Matlab 求解定理1 中式（13）和式（14）可得α=2，μ=0.543。由式（15）可得h2＜，再根据不等式h＜h2，可设定固定脉冲时间间隔h=0.3，结合定理1 式（16）计算可得误差边界为0.366。由于本文使用事件触发控制，且事件触发条件表示为：Fi(t)=，则设定事件触发条件的参数为γ=0.1，η=0.1。

图2 是智能体xi1(i=0，1，2，3，4)和智能体xi2在事件触发脉冲控制下的运行状态。可以看出智能体的状态由离散逐渐收敛，但并没有达到一致，而是在一定范围内波动，即达到了均方有界一致。

图2 例1中xi(i=0，1，…，4)在事件触发脉冲控制下的状态Fig.2 States of agents xi(i=0，1，…，4) under event-triggered impulsive control in example 1

由于欺骗攻击随机发生，为了减少仿真结果的误差干扰，运行程序50 次，并计算‖ζ(i)(t)‖(i=1，2，…，50)的值取平均，并把平均值定义为平均误差。图3 是在固定脉冲时间间隔与事件触发脉冲控制下智能体的平均误差，图中虚线的数值为误差边界0.366。从图3（a）、（b）可以看出智能体的平均误差均小于给定的误差边界，而且在事件触发脉冲控制下，平均误差的收敛更快。

图3 固定脉冲时间间隔与事件触发脉冲控制下智能体的平均误差Fig.3 Average error of agents under fixed impulsive time intervals and event-triggered impulsive control

图4 为事件触发控制下智能体的脉冲时间序列，数值为0 表明没有脉冲，数值1、2、3、4 则分别代表跟随者智能体x1、x2、x3、x4的脉冲次数。可以看出，事件触发脉冲控制能够根据智能体的运行情况，有效地调节脉冲时间间隔，从而合理地调节脉冲次数，更快地达到一致性。

图4 事件触发脉冲控制下跟随者智能体的脉冲间隔Fig.4 Impulsive intervals of follower agents under event-triggered impulsive control

图5 则分别给出了4 个智能体在网络攻击概率为0.1 时遭受网络攻击的次数，其中数值为1 代表智能体遭受到攻击，数值为0 则智能体未遭受到攻击。从图5 可以看出，遭受攻击的次数符合攻击概率0.1。

图5 智能体遭受攻击的次数Fig.5 Number of attacks on agents

例2：不同于例1 中的网络图中存在以领导者为根节点的有向生成树，例2 的拓扑图则不包含以领导者为根节点的有向生成树，其节点数和网络拓扑结构如图6 所示，图中数字0 代表领导者智能体，数字1～4 代表跟随者智能体，对应的拉普拉斯矩阵为：

例2 中相关的矩阵和参数与例1 中的设置相同，仅在网络拓扑结构上作出改变。由图6 可以看出领导者与跟随者2有牵引关系，可以表示为D=diag{0，3，0，0}。图7 给出了智能体状态的一维分量和二维分量，由图中可以看出当网络拓扑结构不存在以领导者为根节点的有向生成树时，即不满足文中假设1 时，智能体状态没有达到均方有界一致。

图6 例2的多智能体的网络拓扑图Fig.6 Multi-agent network topological graph of example 2

图7 例2中xi(i=0，1，…，4)在事件触发脉冲控制下的状态Fig.7 States of agents xi(i=0，1，…，4) under event-triggered impulsive control in example 2

4 结语

本文研究了欺骗攻击下多智能体系统的安全一致性问题，结合脉冲控制和事件触发控制，通过线性矩阵不等式设置的一致性参数，利用图论和李雅普诺夫稳定性理论，推导出了多智能体系统一致性误差系统的均方有界收敛条件，并给出了数值仿真的结果。相较于单一的脉冲控制，脉冲控制和事件触发控制相结合能够加快一致性速度，灵活地调整脉冲时间。然而不足的是，本文并没有考虑时延等实际因素，进一步的研究将关注带有时滞的多智能体系统均方有界一致性问题。