Coordinated Planning Transmission Tasks in Heterogeneous Space Networks: A Semi-Distributed Approach

Runzi Liu ,Weihua Wu ,Zhongyuan Zhao ,Xu Ding ,Di Zhou ,Yan Zhang

1 School of Information and Control Engineering,Xi’an University of Architecture and Technology,Xi’an 710055,Shaanxi,China

2 State Key Laboratory of ISN,School of Telecommunications Engineering,Xidian University,Xi’an 710071,Shaanxi,China

3 Key Laboratory of Universal Wireless Communications(Ministry of Education),Beijing University of Posts and Telecommunications,Beijing 100876,China

Abstract: This paper studies the coordinated planning of transmission tasks in the heterogeneous space networks to enable efficient sharing of ground stations cross satellite systems.Specifically,we first formulate the coordinated planning problem into a mixed integer liner programming (MILP) problem based on time expanded graph.Then,the problem is transferred and reformulated into a consensus optimization framework which can be solved by satellite systems parallelly.With alternating direction method of multipliers(ADMM),a semi-distributed coordinated transmission task planning algorithm is proposed,in which each satellite system plans its own tasks based on local information and limited communication with the coordination center.Simulation results demonstrate that compared with the centralized and fully-distributed methods,the proposed semi-distributed coordinated method can strike a better balance among task complete rate,complexity,and the amount of information required to be exchanged.

Keywords: heterogeneous space network;transmission task;task planning;coordinated scheduling

I.INTRODUCTION

Benefiting from the extensive coverage and flexible networking capability,space platforms(such as satellites,UAVs (Unmanned Aerial Vehicles) or airships on high altitude platform stations) have played an irreplaceable role in areas such as ubiquitous communication,remote sensing,aerospace measurement and control,air transport and so on [1-3].With the development of space technology and the prosperity of commercial space,both the number of space platforms in orbit and the capability of their payloads to acquire data experience a remarkable surge[4].On account of the explosive growth of onboard data and the limited number of ground stations,how to plan transmission tasks efficiently so that the data can be downloaded to the ground in time become more and more significant[5,6].

Satellite systems have long been developed in a chimney-like structure[7].They are generally locked down to a specific space mission,and constructed and managed separately[8].(For example,Chinese Huanjing satellite system is developed for environment and disaster monitoring and forecasting and managed by Ministry of Ecological Environment,while Gaofen satellite series is constructed for the high-resolution remote sensing of territory,which is operated by Ministry of Land Resources [9].) Each satellite system has several dedicated ground stations.However,the number of ground stations owned by each satellite system is limited,on account of the restrictions on site selection and high construction costs.Since the transmission tasks always distribute nonuniformly in space-time dimension,the no-sharing of ground stations among satellite systems may lead to serious resource underutilization.For example,the ground stations of some satellite systems may have heavy load which causes that the onboard data cannot be downloaded in time,while the ground stations of other satellite systems are idle at the same time.

With the application of new technologies such as software defined radio and resource virtualization in space networks [10,11],the technology of sharing ground stations among different satellite systems become mature [12].In recent years,heterogenous space networks,such as Global Education Network for Satellite Operations(GENSO)[13]and Mobile Cube-Sat Command and Control(MC3)ground station network [14],are constructed to support sharing ground stations among worldwide educational departments,and among US government organizations,contractors,universities,and foreign partners.

Although the problem of planning transmission tasks in single satellite systems has been extensively studied[5,6,15],the research on the coordinated task planning in heterogeneous space networks composed of multiple satellite systems is very limited.In literature [16],a central server is added in the heterogeneous space network,which centralizedly plans all the tasks based on the global information collected from satellite systems,and send planning results back to them for execution.Similarly,in literature [17] the operation control centers of all the satellite systems are merged into a super operation control center,and a centralized ant colony-based planning algorithm is proposed to manage the resources of the whole network.However,because the problem of transmission task planning is NP-complete [18],centralized planning for the entire network is of great computational complexity.What’s worse,at the present stage,satellite systems are usually controlled by different armed forces or government agencies.That is,the centralized task planning method is impractical for these satellite systems which cannot be managed by or completely open their task and resource information to a unified agency.Different from the works on centralized coordination,literature [19] proposes a fully distributed coordinated scheduling strategy,which enables the cross-system scheduling of receiving resources by peer-to-peer negotiation.It has much lower computational complexity than centralized methods,and requires space systems to share no more information than the states of shareable resources.Whereas,with the growing number of coordinated satellite systems,a satellite system may need to share resources with many systems at the same time.In this case,the peer-to-peer negotiation lacks global information,so that has poor convergence performance.

To combine the advantages of centralized and fully distributed methods,this paper proposes a semidistributed method for the coordinated task planning problem of heterogeneous space networks,in which a coordination center is introduced to provide guide messages based on a small amount of global information,so that satellite systems can plan tasks separately to realize the cross-system coordination of ground stations.

To this end,we first formulate the problem of coordinated planning transmission tasks of heterogeneous space networks into a mixed integer linear programming (MILP).Then,the problem is transferred and reformulated into a consensus problem which is convenient to be split and solved in parallel.Afterwards,a semi-distributed algorithm to solve the reformulated problem based on ADMM method is developed.Simulation results validates the advantages of the proposed semi-distributed methods over the centralized and fully-distributed ones.Specifically,compared with centralized strategies,the proposed algorithm has lower computational complexity,and does not need satellite systems to be managed by or provide any information other than that about the shareable recourses to other agency.Compared with the fully distributed strategy,the proposed algorithm not only improves the sum profits of the whole network but also has better convergence speed.

The remainder of this paper is organized as follows.Section II introduces the system model and formulates the coordinated task planning problem in heterogenous space networks.In Section III,the problem is transferred and reformulated to facilitate being split and solved in parallel.Section IV proposes an ADMM based semi-distributed task planning algorithm in heterogenous space networks.The performance evaluation by simulations is presented in Section V,followed by concluding remarks in Section VI.

II.SYSTEM MODEL

2.1 Scenario and Problem Description

Consider a heterogeneous space network as illustrated in Figure 1,which is comprised of a coordination center and serval satellite systems.Each satellite system consists of an operation control center,a number of satellites and ground stations.The satellites and ground stations transmit and receive the onboard data,respectively.The operation centers plan the tasks and manage the resources of their satellite systems.The coordination center coordinates the local planing and scheduling of satellite system to improve the total profit of the heterogeneous space network.

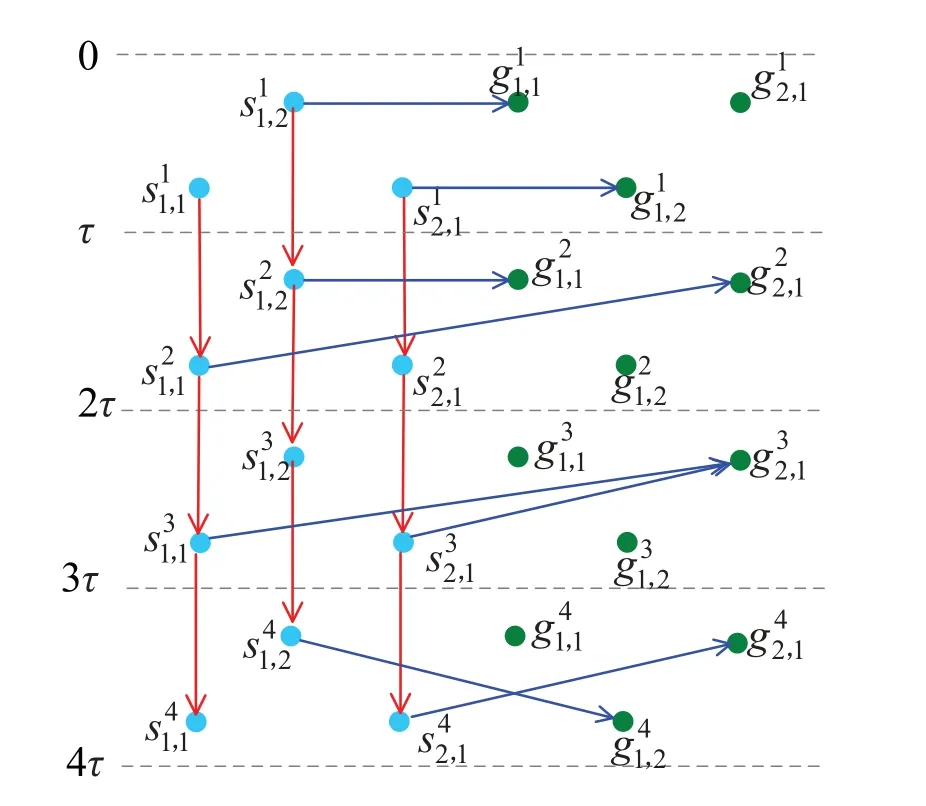
Figure 2. Time expanded graph.

Let symbolndenote thenth satellite system.N={1,2,...,n,...,N}represents the satellite system set.Letsn,idenote theith satellite in thenth satellite system,andSn={sn,1,sn,2,...,sn,i,...}denote the set of satellites of satellite systemn.There are two kinds of ground stations:shareable ground stations and nonshareable ground stations.The shareable ground stations can receive the data from the satellites belonging to any satellite system,while the non-shareable ground stations can only receive the data from the satellites of the same satellite system.Letgn,iandrepresent theith ground station and the the ground station set of satellite systemn.The termare the set of shareable ground stations and the non-shareable ground stations of satellite systemn,respectively.The set of the satellites and ground stations of the entire heterogeneous space network are expressed by

When satellites and ground stations are visible,wireless links can be established to download the onboard data.There are two kinds of downloading links,namelylocal linksandcoordinated links.Local links are the links from satellites to the ground stations in same satellite system,and coordinated links are the links from the satellites to the shareable ground stations belonging to different satellite systems.Moreover,the coordination center and the operation control centers of satellite systems are connected by terrestrial wired network to guarantee the exchanging of control messages.

In heterogenous space networks,the users (units or individuals) send task requests (e.g.,requests for downloading specific onboard data of certain satellites during given time window) to operation control center through terrestrial networks.LetOM=∪1≤n≤N OMndenote the set of tasks in the heterogeneous space network,whereinOMn={omn,1,omn,2,...,omn,h,...}is the set of tasks of satellite systemn.omn,his thehth task of satellite systemn.Each task request can be described by a 5-tuple,i.e.,omn,h=[sn,σ(n,h),bn,h,stn,h,etn,h,wn,h],whereσ(n,h)is the index of the downloading satellite of taskomn,h,i.e.,the data of taskomn,hare downloaded to the ground by satellitesn,σ(n,h).bn,hdenotes the amount of data of taskomn,hrequired to be downloaded to the ground,andwn,hrepresents the profit can be obtained ifomn,his successfully executed.stn,handetn,hare the earliest start time and latest end time of taskomn,h,respectively.The data of taskomn,his assumed to arrive satellitesn,σ(n,h)atstn,h,and would be deleted from the storage ofsn,σ(n,h)if have not been transmitted atetn,h.

For taskomn,h,it is referred to be successfully executed if all of its data can be downloaded to ground stations within time interval [stn,h,etn,h].Note that the presence of tasks is informed to ground stations with the commands by the operation control center through terrestrial networks.The problem of coordinated transmission task planning is to allocate feasible ground stations and downloading windows for the tasks towards maximizing the sum profit of the whole heterogeneous space network.

2.2 Network Model

During the orbital movement,satellites can only transmit to ground stations when flying into their communication ranges.The data of tasks are transmitted through a store-carry-forward paradigm[20].This implies that,besides the limited transmission and storage resources of satellites and ground stations,dynamic network topology is also an important factor on allocating ground stations and transmission windows for the task requests.

We use the time expanded graph (TEG) [21-23]to model heterogeneous space networks.To be specific,we split the planning horizon intoKequal length time slots.The time expanded graphGK(V,A) is aK-layered directed graph,as illustrated in Figure 2,where each layer depicts the network topology of the corresponding slot.Vdenotes the vertex set andArepresents the arc set.

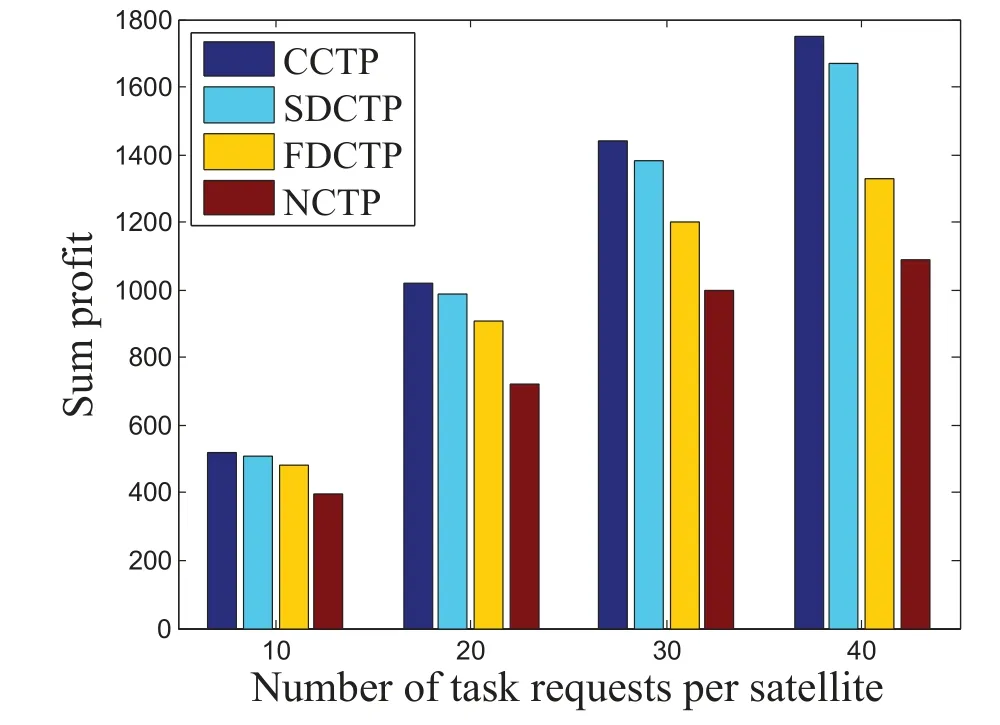
Figure 3. Sum profit versus the number of tasks requests per satellite.

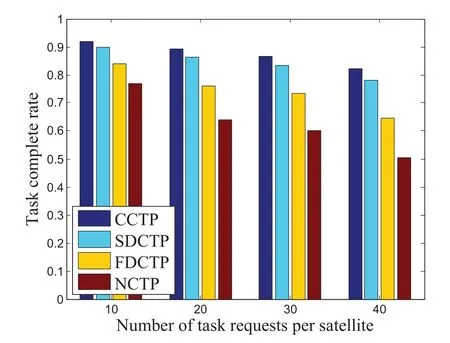
Figure 4. Task complete rate versus the number of tasks requests per satellite.

The vertices in TEG represent the temporal replicas of the satellites or ground stations for every time slots,and the vertex set can be expressed asV=VS ∪VG,whereVSis the set of satellite vertices,which is given by

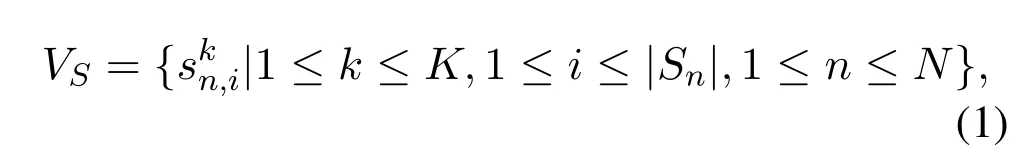
represents satellitesn,iin thekth time slot.Similarly,the set of vertices representing ground stations is expressed as

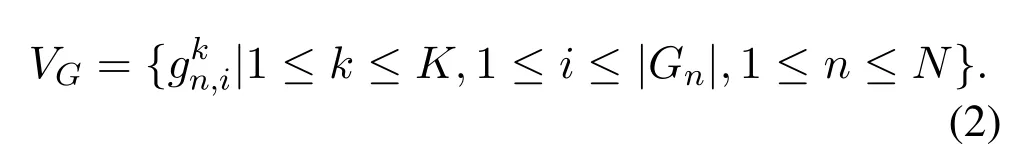
There are two types of arcs in TEG,namely link arcs and storage arcs,which represent the transmission and storage resources of the heterogeneous space network in different time slots.The set of arcs is denoted byA=AL∪AS.Specifically,link arcs represent the feasible downloading links of different time slots.Since there are two kinds of downloading links in the network,the link arc set is also composed of two parts,i.e.,ALLis the set oflocal linkarcs,which is defined as

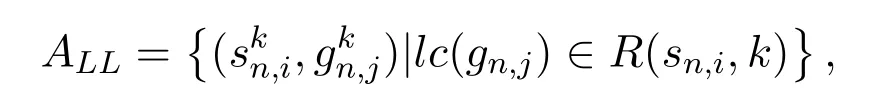
wherelc(gn,j) represents the location of ground stationgn,j,andR(sn,i,k) is the communication range of satellitesn,iin thekth slot.ALCis the set ofcoordinated link arcset,which is expressed as

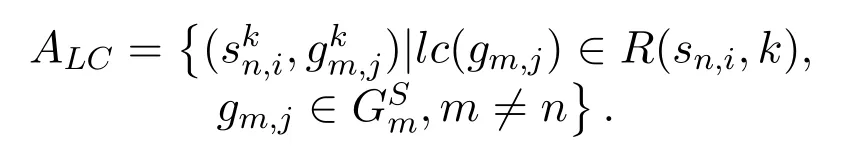
The capacity of a link arc represent the capability of the corresponding link to transmit task data,which is given by

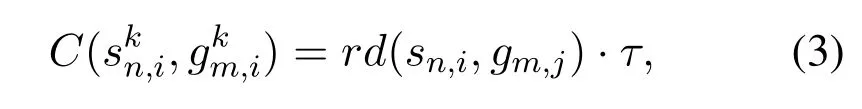
whererd(sn,i,gm,j) is the transmission rate of link(sn,i,gm,j),andτis the length of a slot.The storage arcs model the storage capability of satellites,and the set of storage arcs is given by

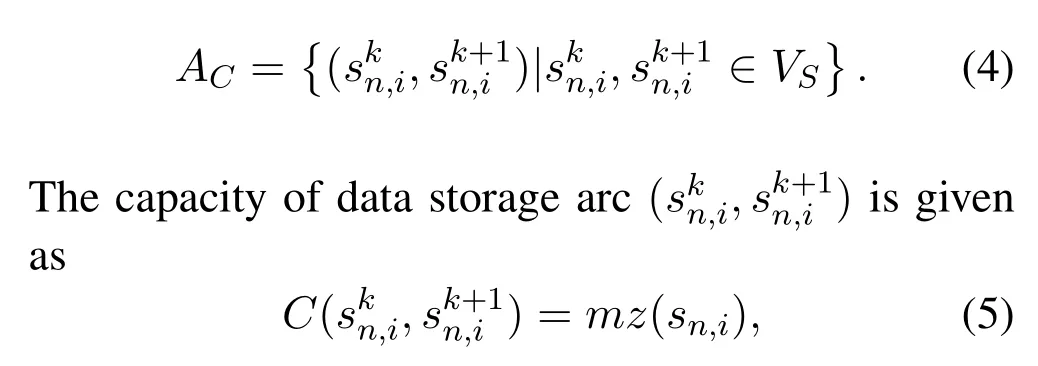
mz(sn,i)is the memory size ofsn,i.

The time expanded graph models the topology evolution of heterogeneous space networks.The flows in TEG represent the storage and transmission process of task data.More specifically,the link/storage arcs passed by a flow represent the set of storage/-transmission resources occupied by the corresponding task,and the value of flow represents the amount of data stored or transmitted [23].Through the variety of link arcs and the capacity of arcs on flows,TEG characterizes the coupled impacts of dynamic network topology and resource capabilities on the task execution process.

2.3 Problem Formulation

In this subsection,the coordinated planning problem of transmission tasks in heterogeneous space networks are formulated into the multi-community flow problem in TEG.First of all,the task requests of the heterogenous space network are modeled by the characteristics of flows in TEG.The execution process of taskomn,his represented by flowfn,hwhich is originated from vertexand destined to vertex setin TEG,wheredenote the index number of the start and the end slot of window[stn,h,etn,h].The restriction thatfn,honly traverses in theskn,h～ekn,hth layers ensures that the data of taskomn,honly be transmitted within its scheduling window in the corresponding execution process.

The coordinated planning problem of transmission tasks of heterogeneous space networks is formulated into the flow problem that optimizes the value of flow and schedule of link arcs on TEG to maximize the sum profit,which is given as follows

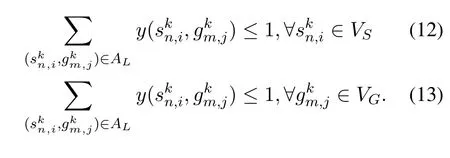
In P1,constraint Eq.(6)means that if a task is successfully planned,the value of its corresponding flow in TEG should equal to the volume its task data;otherwise,the value of the corresponding flow should be zero.This ensures that all the data of the each successfully planned task must be involved in its execution process.Eq.(7)-(9)are flow conservation constraints.Specifically,Eq.(7)and Eq.(9)are the flow conservation constraints for the start and end slot of the schedule window of tasks,and Eq.(8) is the flow conservation constraint for the intermediate slots.The flow conservation constraints ensure that for each task,the amount of data in the storage of its requested satellite at the beginning of a slot is equal to the amount of data transmitted in the slot plus the amount of data remaining in the storage at the end of the slot.Eq.(10) and Eq.(11) are the link capacity constraints for storage arcs and link arcs,which restricts the sum of value of the flows on an arc should be no more than the arc capacity.More specifically,Eq.(10)ensures the amount of data stored in satellites to no more than their storage capacity in each slot,whereFkn,iis the set of flows corresponding to the tasks of which the downloading satellite issn,iand the schedule window contains thekth slot,i.e.,

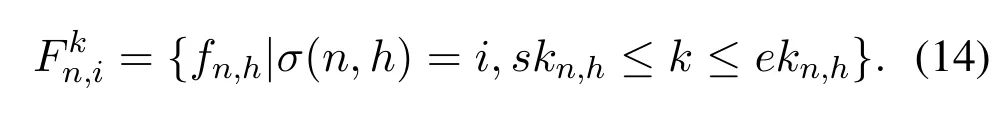
Due to the limit of the transceivers of satellites and ground stations,a satellite can only communicate with a ground station at the same time,and vice versa.That is,even if a satellite and a ground station are visible to each other in a slot,the link may not be established due to the contention with other links.Therefore,link schedule conflict constraints Eq.(12),Eq.(13)are introduced to avoid the conflicts of link scheduling.To be specific,Eq.(12) ensures that each satellite only transmit to a ground station in a slot,and Eq.(13)imposes that each ground station can only receive data from one satellite in a slot.

III.PROBLEM TRANSFORMATION AND REFORMULATION

3.1 Problem Transformation

It can be observed that P1 is an MILP problem [24],which is NP-hard in general [25].In order to solve the problem P1 in polynomial time,we first relax the integer variables as follows,

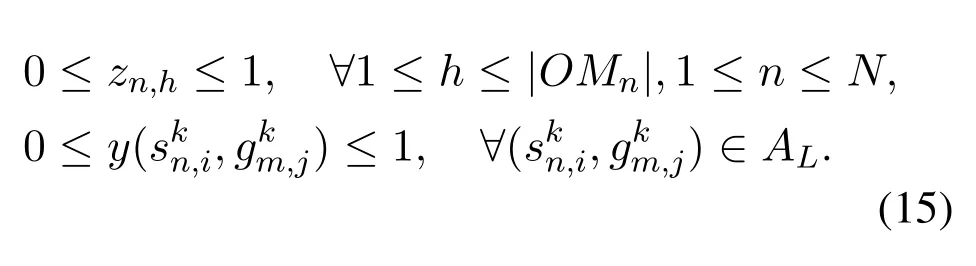
Then we transform the constraints Eq.(7)-Eq.(10)of P1 to reduce the number of variables and coupled constraints required to be separated,so that reducing the complexity of decomposing P1.Specifically,for a flowfn,h ∈F,the expansion of its flow conservation constraints is

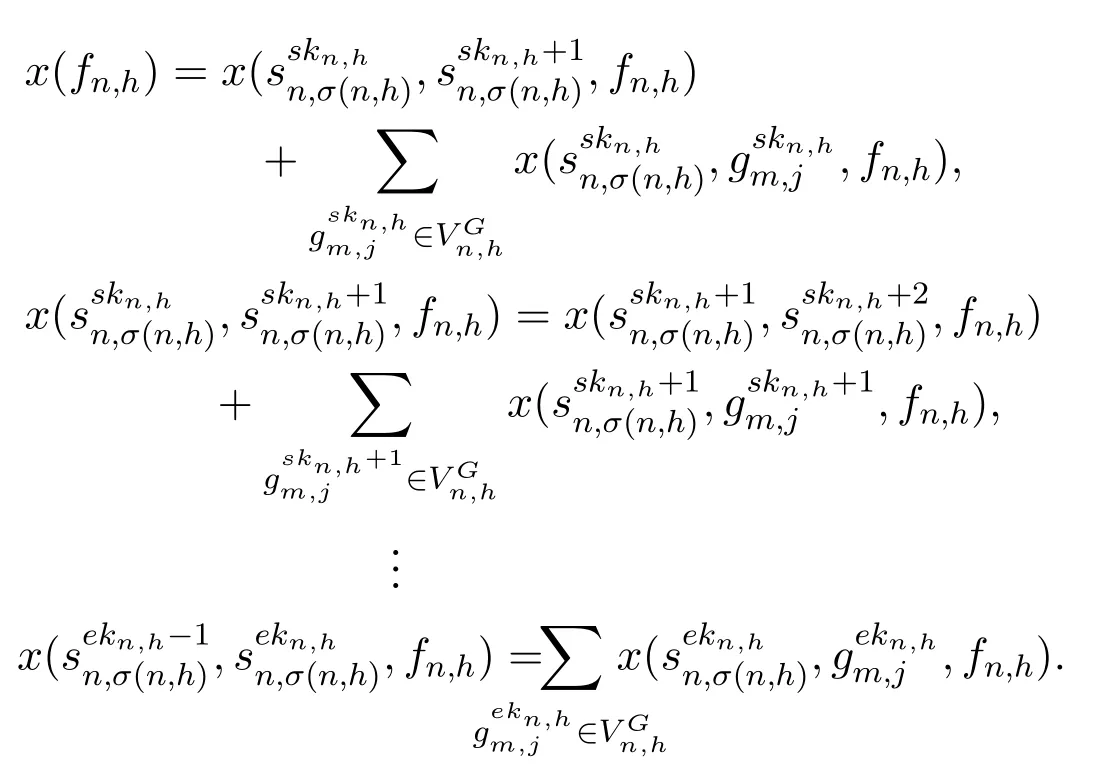
Adding the left and right sides of the above equations,respectively,we can derive the following equation

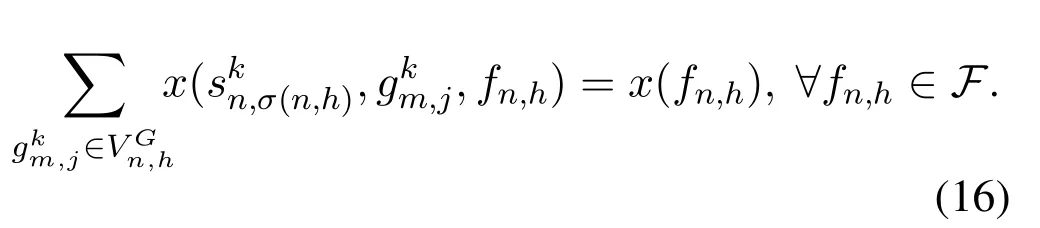
Compared with the flow conservation constraints Eq.(7)-Eq.(9) in P1,Eq.(16) does not include the flow variables on storage arcs.In order to retain the effect of the capacity constraint for storage arcs in Eq.(10),we use the flow variables (i.e.,on link arcs to express those on storage arcs,i.e.,

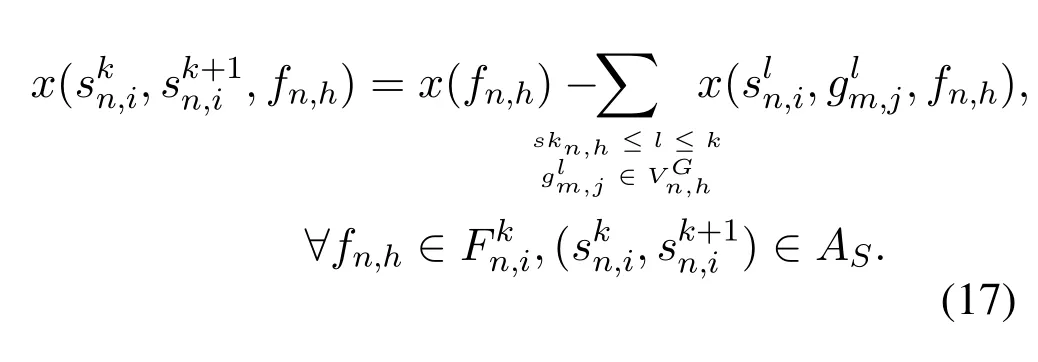
By substituting Eq.(17) into Eq.(10),the capacity constraint for storage arcs can be reformulated as

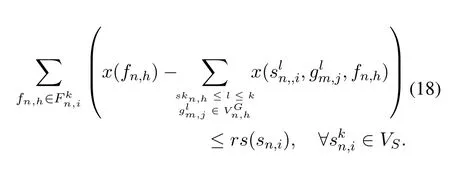
In summary,by relaxing the integer variables and replacing constraints in Eq.(7)-Eq.(10)with Eq.(16)and Eq.(18),problem P1 is transferred into

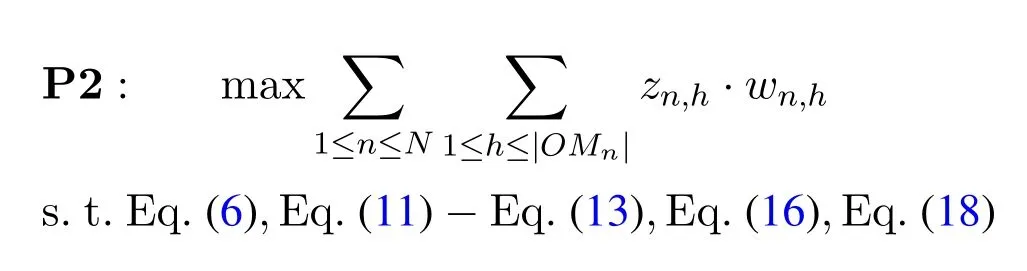
It can be observed that P2 is a linear programming problem,and the number of variables and constraints of P2 are much smaller than those of P1.In order to enable the decentralized coordination of transmission task planning in heterogenous space networks,in the next subsection we will reformulate P2 into a form of consensus problem which facilitates being separated with respect to theNsatellite systems.

3.2 Consensus Problem

We can directly divide the objective of P2 with regard to theNsatellite systems,but due to Eq.(12) and Eq.(13),variableis a global variable coupled with both satellite systemnand satellite systemm,and thus cannot be divided into any one of them.In order to make P2 separable,we introduce the local copies of the global variables.More specifically,for each global variable,two local copies,denoted byare created for satellite systemnandm,respectively.With the local copy variables,we rewrite problem P2 equivalently in a form of global consensus problem as

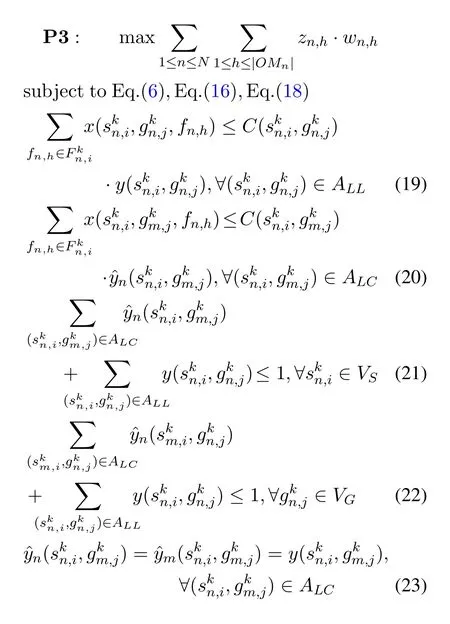
Eq.(23)is the consensus constraint for the local copy variables and global variables.Aside from global variables,all the variables of problem P3 can be separated with regard to satellite systems.Similarly,the constraints except the consensus constraint constitute local constraint sets for each satellite system.Specifically,the local variables of satellite systemnis given by

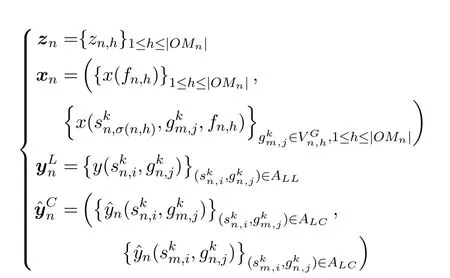
The feasible solution set of the local variables for each satellite systemn ∈Nis given by

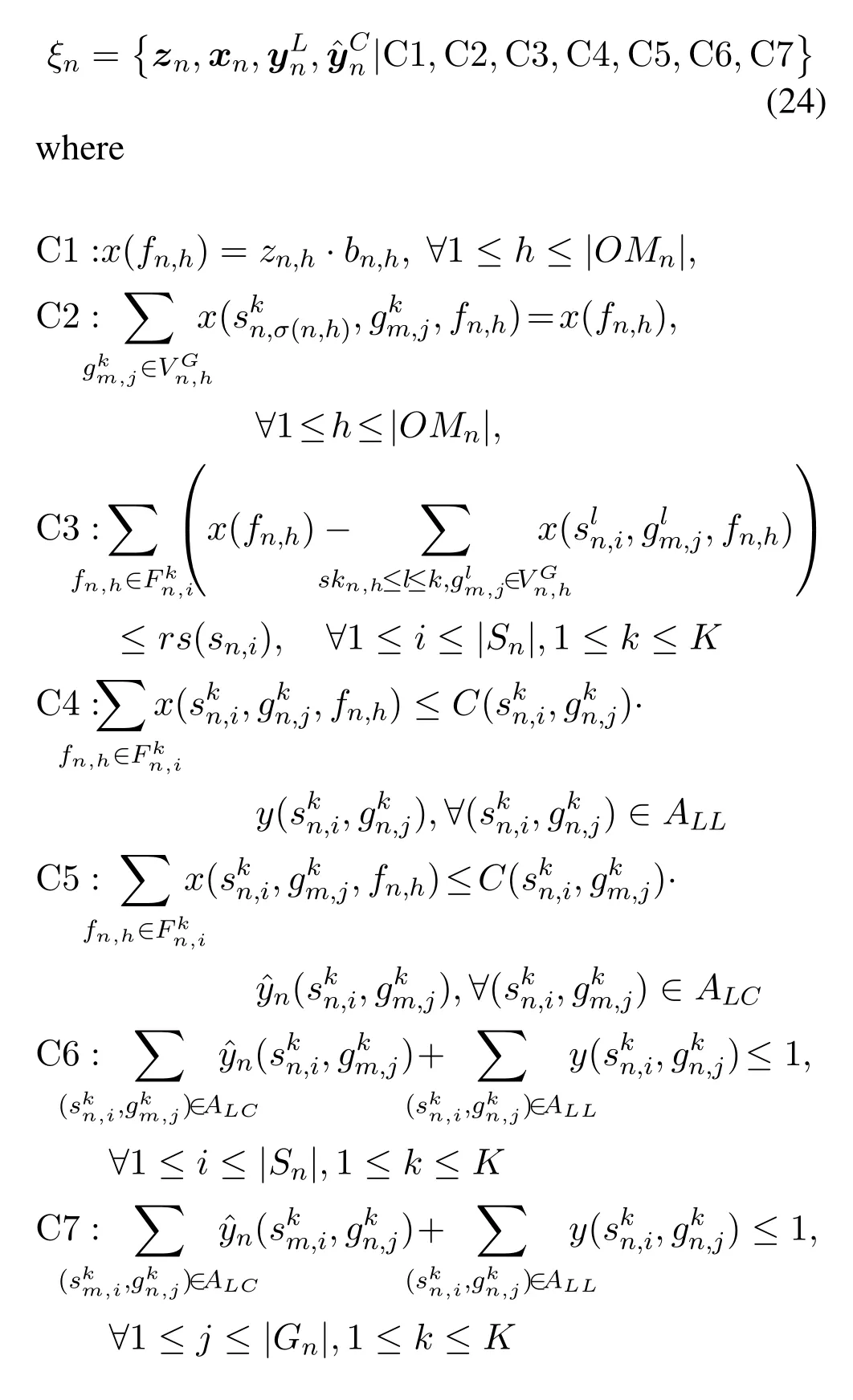
Then we define the local cost function for each satellite systemn ∈N

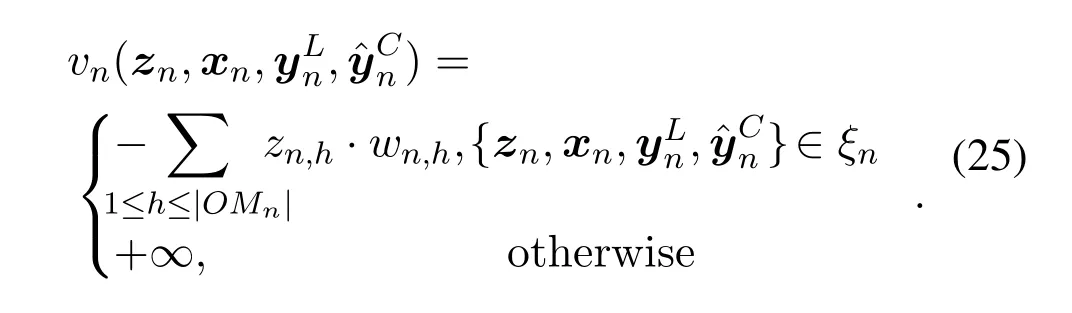
With Eq.(24) and Eq.(25),P3 can be compactly rewritten as

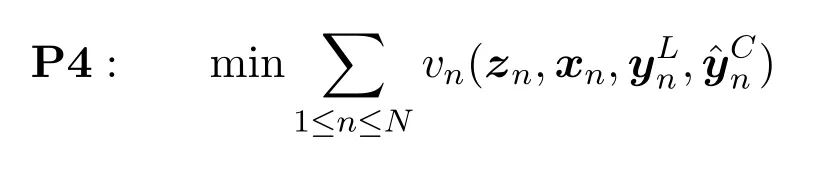
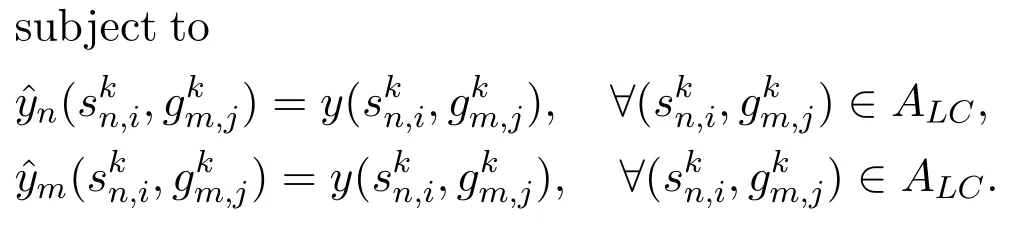
It is evident that the objective function of P4 can be partitioned across all satellite systems in heterogeneous space networks,permitting each system to independently address the associated subproblem.The consensus constraints ensure that the local copies of global variables kept in various satellite systems are consistent.In the next section,we will employ Alternating Direction Multiplier Method (ADMM) [26]to solve the global consensus problem P4 in a semidistributed manner.

IV.SEMI-DISTRIBUTED MISSION PLANNING ALGORITHM BASED ON ADMM

The machinery of applying ADMM to P4 is initiated by forming an augmented Lagrangian with respect to the consensus constraints[26,27],which is expressed as follows

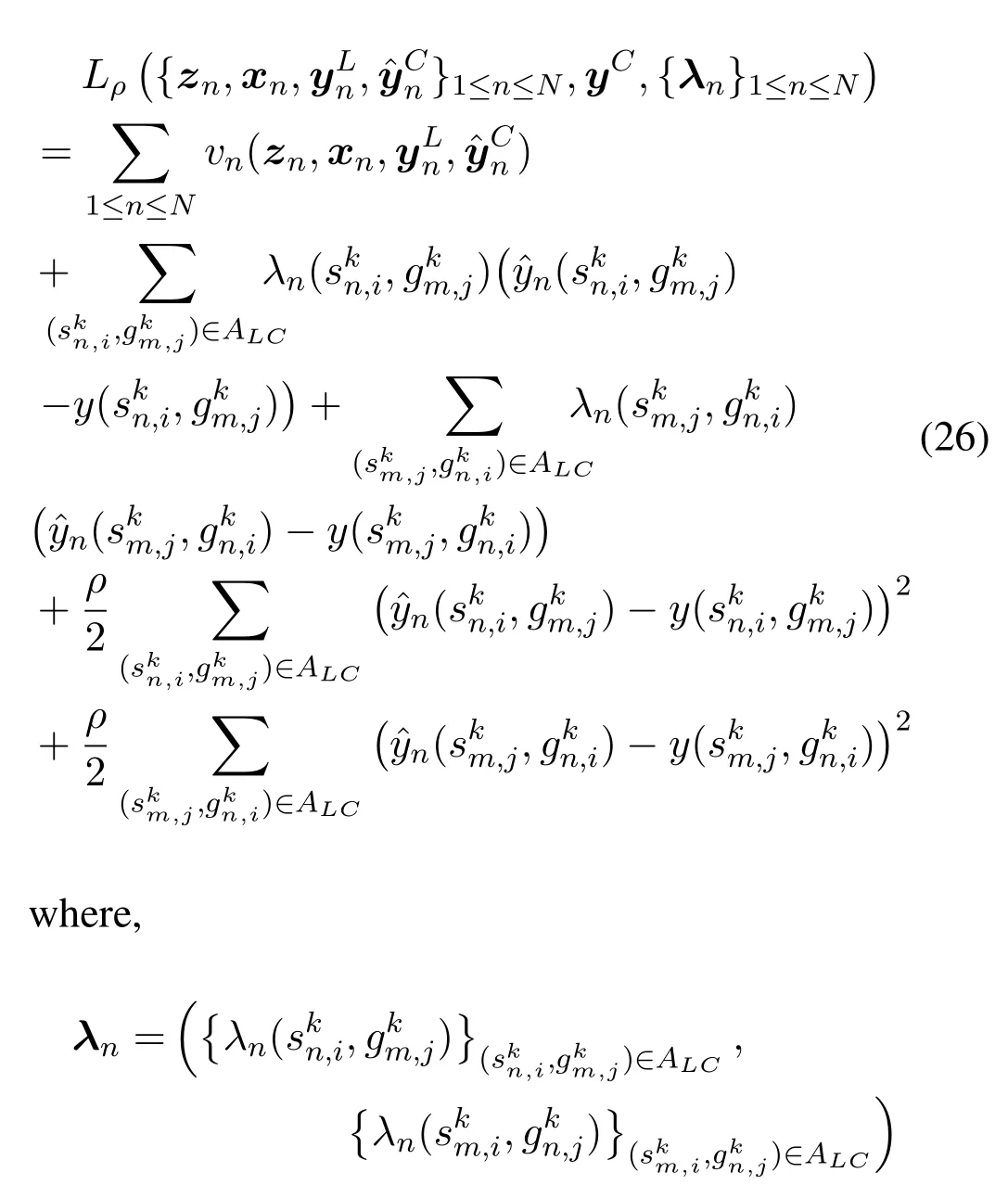
is the Lagrange multiplier associated with the consensus constraints in P4,ρ ∈R++is a penalty parameter,which is a positive constant parameter to adjust the convergence speed of ADMM[28,29].Compared to the standard Lagrangian,the additional quadratic regularization term in augmented Lagrangian facilitates the convergence of the iterative method.Moreover,the solution of original problem P4 is not affected by the addition ofρ-terms,because for any feasible solution,these terms are actually equal to zero.With ADMM applied to P4,the augmented Lagrangian in Eq.(26)is minimized over the local variables and global variables in succession,and then the lagrange multipliers are updated iteratively.Lettdenote the iteration index,problem P4 can be solved by the following sequential iterative optimization steps.

Step1.Local Variables Update

It can be seen from Eq.(27)that the computation of local variables are completely decentralized with respect to the index of satellite systemn,thus can be executed by the operation control centers of satellite systems parallelly.We solve the subproblem for each satellite systemn ∈Nin thet+1th iteration by eliminating the constant terms in Eq.(27):

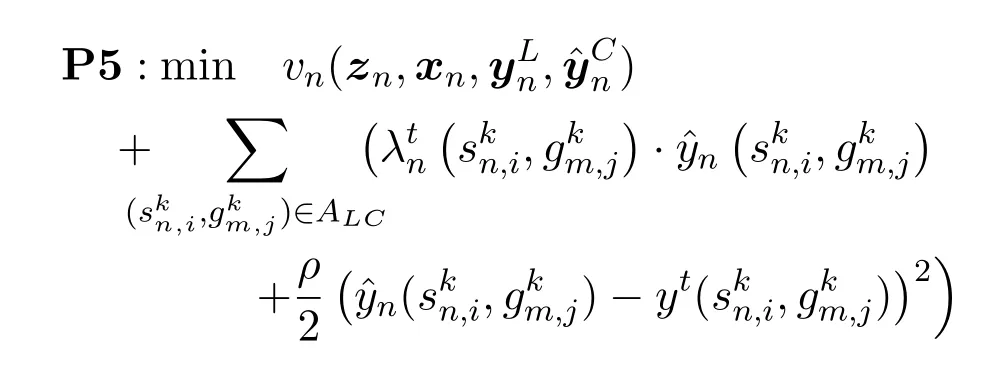
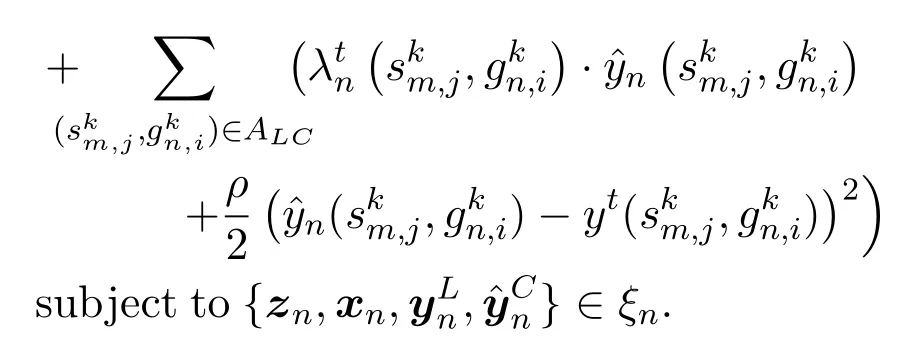
P5 is a convex problem because of its quadric objective function and convex feasible set.As a result,it can be immediately solved using some established techniques like the primal-dual interior-point approach[30]or optimization tools like CVX.

Step2.Global Variables Update

After updating local variables,the global variables are updated through Eq.(28).

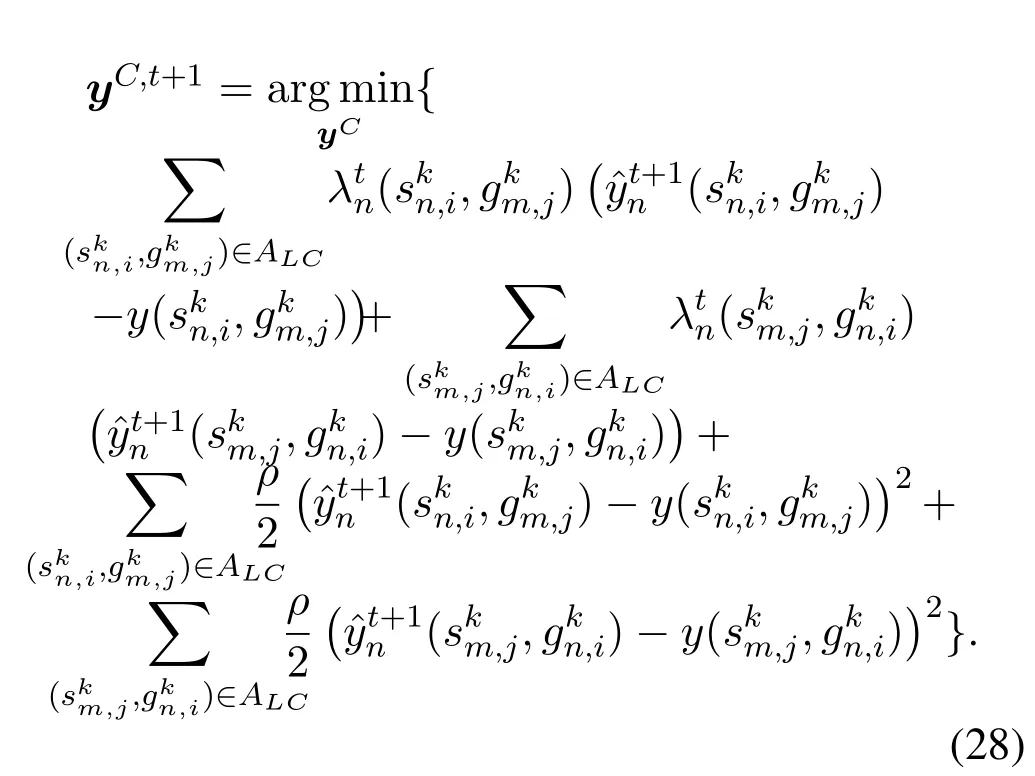
The global variablesyCcan be derived by setting the gradient of Eq.(28) to zero because it is an unconstrained quadratic programming problem and is strictly convex as a result of the additional quadratic regularization terms.That is,

By initializing the Lagrange multiplier as zero,it follows that∈ALCattth iteration[27].Therefore,Eq.(30)can be reduced to

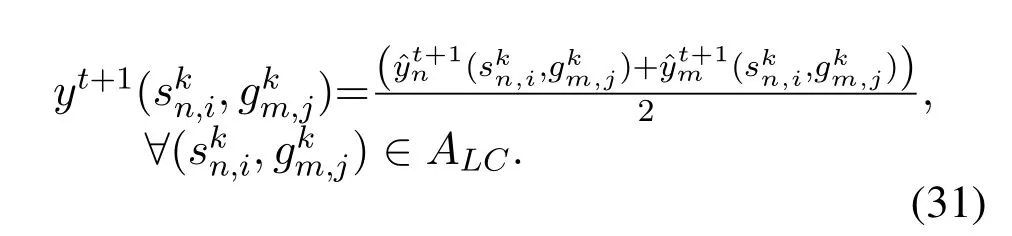
Eq.(31)implies that in each iteration the global variableyt+1(skn,i,gkm,j)can be obtained by averaging over the corresponding local copies of satellite systemmand satellite systemn.

Step3.Lagrange multipliers Update

Using the penalty parameterρas step size,the Lagrange multipliers are updated as follows

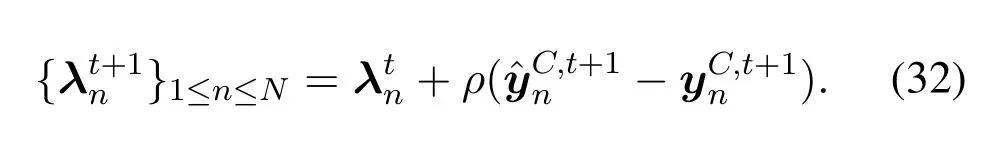
With the local copies and the global variables received from the coordination center,the operation control center of each satellite systems can update the corresponding Lagrange multipliers in parallel through Eq.(32)in each iteration.

It can be observed thatstep 1 and step 3 of the above iterative optimization process are completely separable respect to the satellite systems and can be executed by their operation control centers in parallel,while step 2 should be executed by the coordination center.This implies that the iterative optimization process is semi-distributed and the exchanging of global variableyCand its local copiesbetween the coordination center and the operation control centers of satellite systems are required to implement the iteration steps.

The ADMM-based semi-distributed coordinated planning process is illustrated in Algorithm 1,wherein line 5-7 are the execution of step 1-3 and the associated information exchange between coordination center and satellite systems.Moreover,line 7 indicates the termination criterion of the iteration.That is,when the difference of global variables caused by update become sufficient small or the number of iteration exceeds the threshold,the coordination center informs each operation control center to terminate the iteration,whereεis a small positive constant scalar.Since we have relaxed binary variablesyandzof the original problem P1,after the sequential iterative optimization steps,the global relaxed variablesyCand the local relaxed variables,znare recovered by coordination center and the operation control center of satellite systems through Algorithm 2 and Algorithm 3,respectively.

The recovery algorithm of global relaxed variablesyCfor coordination center is summarized in Algorithm 2.is the set of arcs that conflict with link arc,which is defined as

The recovery algorithm of local relaxed variablesandznfor each satellite systemn ∈Nis summarized in Algorithm 3.It firstly recovers the local link scheduling variablethrough the same method of Algorithm 2 (line 2-16).is the set of arcs that conflict with link arc.Then the task planning variableznis recovered through the sequential fixing method(line 18-25)of which the main idea is to solve a series of problem P5 with fixed binary variables iteratively,and use the solutions as a guideline to fix the unrecovered relaxed variables.Specifically,in each iteration,we first solve problem P5 of which the recovered binary variables are fixed,then fix the uncovered task planning variables with the minimum value to zero.This process is repeated until the value of all the unfixed task planning variables are 1.

It can be observed from Algorithm 1-3,during the coordinated task planning process,only the scheduling variables of coordinated links and their local copies(i.e.,yCand) are required to be exchanged between coordination center and the operation centers of each satellite system.In other words,each satellite system only needs to provide the scheduling results of associated coordinated links to the coordination center,while no more detailed information of these links(e.g.,bandwidth and the tasks transmitted when being scheduled) is required to be disclosed,let alone any information about its task requests and non-shareable ground stations.

V.SIMULATIONS

In this section,simulation results are presented to validate the efficiency of the proposed semi-coordinated task planning algorithm for heterogenous space networks.We conduct a simulation scenario which is composed of four satellite systems,which have 4,4,6,6 satellites,respectively.All the satellites are in sun-synchronous orbits at height from 600km to 1000km.Each satellite system has two ground stations: one shareable ground station and one nonshareable ground station.The eight ground stations are located in Sanya,Jiamusi,Beijing,Kashi,Xiamen,Johannesburg,Xian and Swakopmund.Each satellite has a 200Gbit storage capacity,and the links between them and the ground stations have a bandwidth of 50Mbps.The planning horizon is 86400s,during which there are 10-40 transmission tasks for each satellite to transmit.For each task,the amount of data to be transmitted is 5-15Gbit,and the profit is an integer randomly distributed in[1,5].The earliest start time of tasks are uniformly distributed within the planning horizon,and the latest end time is 30min-3h later than the earliest start time.In order to verify the performance of the ADMM-based Semi-Distributed Coordinated Task Planning(SDCTP)algorithm proposed in this paper,we employ the following three planning strategies for comparison,which are illustrated in Table 1.

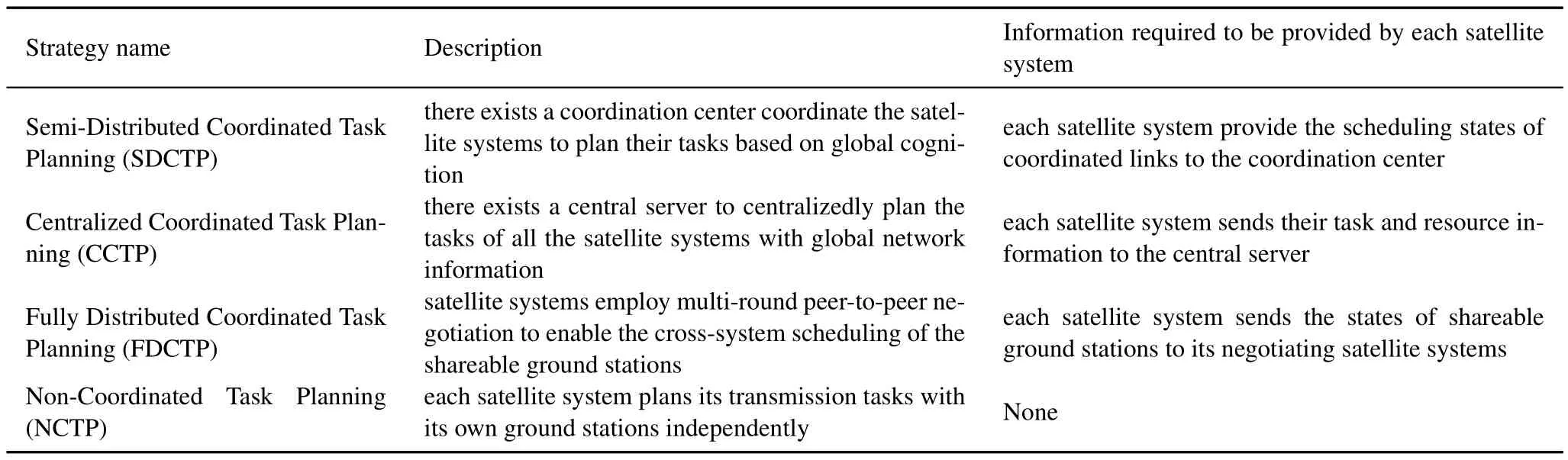
Table 1. Comparison of the task planning strategies tested in simulations.

Figure 3 and Figure 4 show the sum profit and task complete rate of different task planning strategies with varying numbers of the tasks of each satellite.It can be seen that the performance of SDCTP algorithm proposed in this paper is very close to that of CCTP strategy.Note that CCTP can be used as a benchmark since it is a centralized coordinated task planning algorithm with the most ideal condition in the four algorithms.When the number of tasks is large,our algorithm can achieve about 25.4%and 53.1%profit gain compared with FDCTP and NCTP strategy,respectively.This is because both FDCTP and our SDCTP strategy support sharing ground stations among multiple satellite systems,which provides additional opportunities for the tasks which cannot be completed with the ground stations of its own system.Nevertheless,in FDCTP strategy,the cross-system scheduling is made based on the local information of the satellite systems participating peer-to-peer negotiation,while in the proposed algorithm,the coordination of the shareable ground stations of satellite systems are guided by coordination center from a global perspective.Figure 4 shows that with an increase of the number of tasks,the complete ratio of all the four algorithms decreases.This trend is expected,because given the limited resources,increasing the number of tasks makes the whole net-work more heavily loaded,which in turn reduces the task complete ratio.

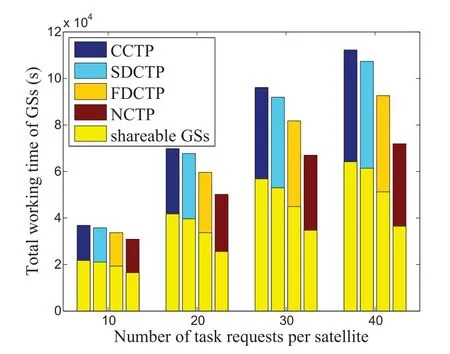
Figure 5. Total working time of all the ground stations/shareable ground stations versus the number of tasks requests per satellite.

To further understand the performance gain,the total working time of the ground stations of different task planning strategies are depicted in Figure 5.The working time of a ground station is the sum time used to receive data from satellites in the plan horizon.In Figure 5,each bar presents the total working time of all the ground stations (i.e.,the sum of the working time of all the ground stations in heterogenous space networks) under different planning strategy,and the yellow part of each bar presents the part of working time contributed by the shareable ground stations.It can be seen that the working time of shareable ground stations is about half of the total working time under NCTP strategy,which implies the working time of shareable and non-shareable ground stations are basically the same.In comparison,the working time of shareable ground stations is evidently higher than that of non-shareable ground stations under the three coordinated task planning strategies.This implies that the gain of coordinated task planning strategies of heterogeneous space networks mainly comes from the additional opportunities provided by the shareable ground stations for the tasks which cannot be completed in time thorough the ground stations of its own system.Furthermore,when the number of the task requests is large,our SDCTP algorithm improves not only the average working time of shareable ground stations,but also that of non-shareable ground stations evidently over FDCTP strategy.This is because when the shareable ground stations become saturated with the growth of task number,the proposed SDCTP algorithm can schedule the non-shareable ground stations to complete more local tasks which may conflict with the tasks from other satellite systems with the global view of the coordination center,so that enables the shareable ground stations to provide more opportunities for tasks that cannot be completed in time in their own satellite systems.

Figure 6 compares the computation time of different task planning algorithms.It can be observed that the NCTP algorithm has the minimum computation time,and the computation time of our SDCTP algorithm is lower than that of CCTP and FDCTP algorithm.This is because the size of centralized planning problem is much larger than the distributed ones,due to the joint planing of the whole network.In FDCTP strategy,each satellite system can only negotiate with one other satellite system based on their local information at a time,thereby having low convergence speed.

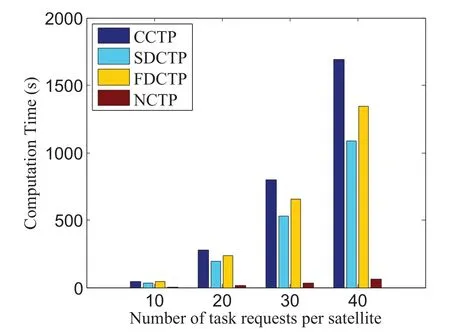
Figure 6. Computation time versus the number of tasks requests per satellite.

VI.CONCLUSION

This paper proposed a semi-distributed coordinated planning algorithm for transmission tasks in heterogeneous space networks.Firstly,the coordinated task planning problem towards maximizing the sum profit of heterogeneous space networks was formulated into an MILP.Then,we transferred and reformulated the problem into a consensus optimization framework which is convenient to be solved by satellite systems in parallel.With the application of ADMM,the problem was decomposed into locally solvable subproblems.On this basis,a semi-distributed coordinated task planning algorithm for heterogeneous space networks was designed.Simulation results show that,compared with the centralized and fully distributed coordinated methods,the proposed algorithm can strike a better balance among task complete rate,complexity,and the amount of information required to be exchanged.

ACKNOWLEDGEMENTS

This work was supported in part by the NSF China under Grant (61701365,61801365,62001347),in part by Natural Science Foundation of Shaanxi Province(2020JQ-686),in part by the China Postdoctoral Science Foundation under Grant(2018M643581,2019TQ0210,2019TQ0241,2020M673344),in part by Young Talent fund of University Association for Science and Technology in Shaanxi,China(20200112),in part by Key Research and Development Program in Shaanxi Province of China(2021GY-066),in part by Postdoctoral Foundation in Shaanxi Province of China (2018BSHEDZZ47),and the Fundamental Research Funds for the Central Universities.