Secrecy Transmission of NOMA-OTFS Based Multicast-Unicast Streaming

Junfan Hu ,Jia Shi,* ,Xianyu Wang,2 ,Xiaoju Lu ,Zan Li ,Zhuangzhuang Tie

1 The State Key Laboratory of Integrated Services Networks,Xidian University,Xi’an 710071,China

2 Academy of Space Electronic Information Technology,Xi’an 710100,China

3 Unit 69036 of PLA,Urumqi 830000,China

Abstract: This paper investigates the security performance of a cooperative multicast-unicast system,where the users present the feature of high mobility.Specifically,we develop the non-orthogonal multiple access(NOMA)based orthogonal time frequency space (OTFS) transmission scheme,namely NOMAOTFS,in order to combat Doppler effect as well as to improve the spectral efficiency.Further,we propose a power allocation method addressing the trade-off between the reliability of multicast streaming and the confidentiality of unicast streaming.Based on that,we utilize the relay selection strategy,to improve the security of unicast streaming.In the context of multicastunicast streaming,our simulation findings validate the effectiveness of the NOMA-OTFS based cooperative transmission,which can significantly outperform the existing NOMA-OFDM in terms of both reliability and security.

Keywords: OTFS;NOMA;physical layer security;multicast-unicast

I.INTRODUCTION

As more and more services are involved in multi-user wireless networks,many of these users demand the same data stream.Therefore,in addition to the unicast mode for a single receiver,the multicast transmission,which can deliver common information to multiple users simultaneously,has been incorporated into the Long Term Evolution(LTE)standard[1]due to its potential to effectively improve spectral efficiency and link utilization [2].Further,the scarcity of radio resources and the heterogeneity of wireless applications for 5G and beyond have motivated recent research on multi-user networks with mixed multicast and unicast traffic[3-7].

However,in multicast-unicast networks,the increase of users and the open nature of the wireless channel expose the multicast-unicast streaming to significant security concerns.Currently,physical layer security(PLS)techniques utilize the dynamic features of wireless communications to prevent eavesdroppers from decoding data,while also ensuring that confidential information is received reliably in private [8].Hence,it has been recognized as a supplement to upper-level security approaches to enhance security performance[9,10].In particular,beamforming technology,utilizing the spatial degrees of freedom provided by multiple antennas to adjust the beam orientation,can thus reduce/prevent information leakage to eavesdroppers,which is recognized as one of the most powerful tools for enhancing PLS[11].

To fully unleash the potential of PLS for the multicast-unicast streaming networks,many works have been carried out in the literature.In[12],the secrecy capacity region was derived based on the information theory in a broadcast system with both common and confidential messages.This system was then generalized to the multicast-unicast network[13],where the two transmitted messages were superimposed by superposition coding,and the optimization theory was utilized to obtain the optimal transmit covariance to maximize the unicast secrecy rate with the QoS constraint of the multicast service.Afterwards,[14]extended the multicast-unicast network to the case where aiming to trade off the secrecy rates of unicast signals,as well as to maximize the achievable multicast rate by considering the beamforming design.

On the other hand,current research [15-17] investigated that non-orthogonal multiple access (NOMA)schemes outperform traditional orthogonal multiple access (OMA) schemes in multi-user networks in terms of secrecy performance.The secrecy rate maximization was considered by optimizing the beamforming scheme while guaranteeing a satisfactory quality of service performance in a unmanned aerial vehicle (UAV) aided multi-user network with multicastunicast transmission assisted by NOMA [18].Moreover,in [16],joint power allocation and beamforming strategies were used to enhance the secrecy of the unicasting message while preserving the reliability of the multicast message.By contrast,[19] developed two new power allocation schemes for NOMA networks with multicast-unicast traffic,which improve the outage performance for multicast users and improve the diversity order of the unicast user compared to [16].Unfortunately,the aforementioned excellent schemes are delicately for low-mobility wireless networks.consequently,they can not be directly extended to the high-mobility networks.

With the rapid development of emerging applications,such as the UAV,low-earth-orbit (LEO) satellites,V2X,etc.,future wireless networks are expected to provide reliable and secure communications for users with high mobility.To cope with the high Doppler spread caused by high mobility,orthogonal time-frequency space (OTFS) [20-22] is now emerging as a new solution.In particular,OTFS exploits 2D transformations to covert a doubly-dispersive channel in the time-frequency (TF) domain to an almost constant channel in the delay-Doppler (DD) domain.The sparsity and lower variability of the channel in the DD domain simplify the required channel estimation and signal detection.Benefiting from this,OTFS has the potential to achieve full channel diversity,enabling a reliable transmission in high-mobility scenarios[23,24].

Various works [25-28] have been devoted to study OTFS schemes.In [25,26],the robustness of the OTFS scheme has been evaluated over high Doppler fading channels,using a low complexity signal detection technique.[25] proposed a message passing based algorithm for OTFS signal detection.In addition,[26]designed an attractive hybrid OTFS receiver integrating parallel interference cancellation(PIC)and MAP detection.Further,[27,28]have focused on designing OTFS based multiple-access (MA) schemes,where the proposed MA method [27] was multi-user interference free,while an interleaved time-frequency MA scheme [28] was developed for reducing the detection complexity.It is worth mentioning that recent works[29,30]proposed a new form of NOMAOTFS in which a single high-mobility user using OTFS in the DD domain is paired with a group of low-mobility OFDM users for non-orthogonal channel sharing.However,the related discussions on the secure transmission performance of the NOMA-OTFS scheme were not presented.

To fill the gap in the investigation of the secure transmission properties of the NOMA-OTFS scheme,this paper focuses on studying the security performance of the NOMA-OTFS assisted cooperative multicast-unicast system under high mobility scenarios.Our key contributions include: 1)The guiding interval for power allocation is proposed to address the trade-off between the reliability of multicast streaming and the security of unicast streaming;2) In addition,we analyze the relay selection strategy against the eavesdropping for unicast information;3) We derive the closed-form expressions for the outage probability(OP)of the multicast transmission and the secrecy outage probability (SOP) of the unicast transmission;4)We carry out a comprehensive performance evaluation,where validating the effectiveness of the NOMAOTFS scheme.

II.SYSTEM MODEL &MAIN ASSUMPTION

2.1 Main Assumption

Without loss of generality,we consider a downlink communication scenario,which consists of a base station(BS)andK+1 users with high mobility denoted asUi,for 0＜i ＜Kas shown in Figure 1.Note thatU0is the unicast user without a direct link to the BS,andUi,for 1＜i ＜K,are multicast users.Besides,Eve tries to eavesdrop on the unicast signal.We consider that a multicast userUris selected as a trusted decode-and-forward(DF)relay to helpU0in receiving the unicast message.To improve spectral efficiency,the BS superimposes both multicast and unicast messages by using NOMA technology.In specific,the multicast message is available to all users,while the unicast message is intended only for the unicast user.According to Figure 1,there are two phases of transmission:1)BS transmission,2)Cooperative transmission.

Figure 1. System model of joint multicast-unicast streaming.

2.2 Preliminaries on OTFS Transmissions

Taking into account of the high-speed mobile characteristic of users,it is assumed that both the unicast and multicast messages are based on OTFS scheme.The specific system process of OTFS is shown in Figure 2.At the transmitter,the modulator uses the inverse symplectic finite Fourier transform(ISFFT)to map information symbolsx[k,l]in the DD domain into the TF domain symbolsX[n,m].Then the Heisenberg transform is used to obtain the time domain signals(t)that will be transmitted over the wireless channel.At the receiver,through the Wigner transform,the received time domain signalr(t)is mapped to the TF domain symbolsY[n,m]and then mapped to the DD domain via symplectic finite Fourier transform (SFFT) to obtainy[k,l].

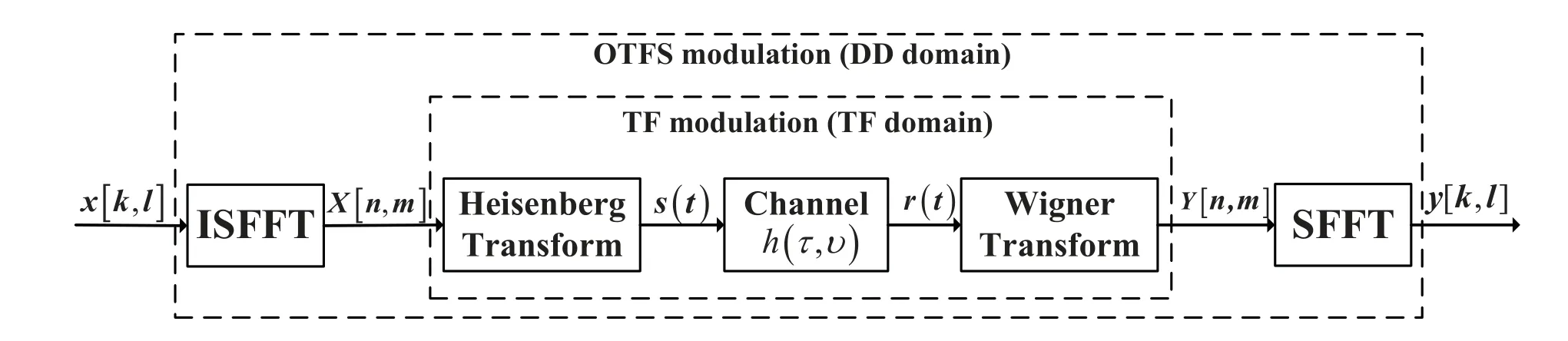
Figure 2. A brief diagram of considered OTFS transmission.

We usehi(τ,v),0＜i ＜Kto denote thei-th user’s channel response in the DD domain.The channel response in the DD domain can be characterized as[20]

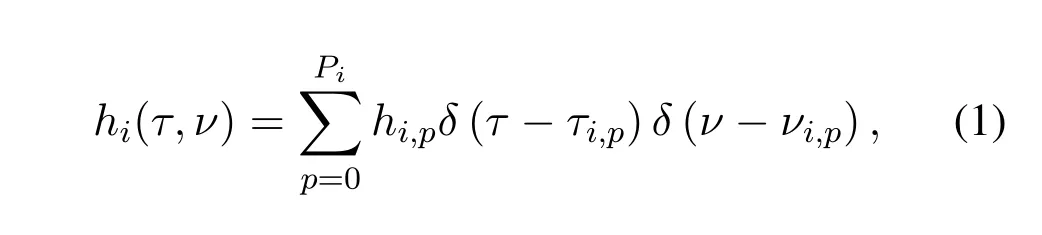
where each userUihasPi+1 propagation paths,hi,p,τi,p,vi,pdenote the channel gain,delay,and Doppler shift on thep-th propagation path ofUi,respectively.We assume that{hi,p,0＜p ＜Pi}are independent and identically distributed (i.i.d.) random variables and obey the Nakagami-mdistribution.

Without loss of generality,let us consider two sets of DD domain information symbolsxM[k,l]andxU[k,l],for 0≤k ≤N-1 and 0≤l ≤M-1,which represent the multicast message and unicast message in the DD domain,respectively.With the application of NOMA,the signal transmitted by the BS is given by

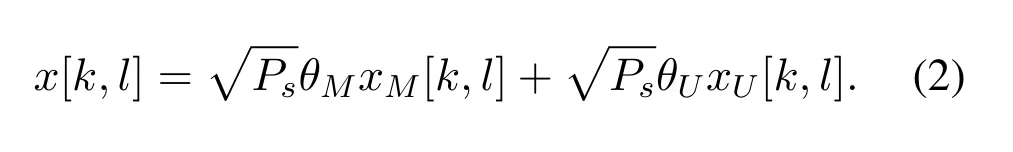
Similarly,the selected DF relayUralso uses NOMA technology in the second phase with the transmitted signal of the formula

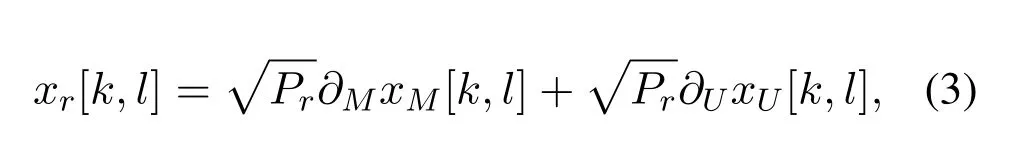
wherePsandPrare transmitted power of the BS and selected relay,θM,∂M,θU,∂Uare the NOMA power allocation coefficient of multicast message and unicast message.Note that

Let us take the first phase as an instance,to describe the OTFS transmission details.Firstly,at the BS,symbolsx[k,l] are mapped intoX[n,m] in the TF domain by ISFFT,form ∈{0,1,···,M -1}andn ∈{0,1,···,N -1},whereNandMare the number of time slots and subcarriers[30].In specific,the TF domain can be partitioned by sampling at intervals ofTand frequency spacing Δf,and the corresponding OTFS frame is with durationNTand the bandwidthMΔf.Next,samplesX[n,m]are transformed into a continuous time domain signals(t)by applying the Heisenberg transform and transmitting pulse.

The signals(t) is then passed through the timevarying channel with a channel impulse responsehi(τ,υ).Letri(t) be the received time domain signal forUi.Then,the Wigner transform is employed to obtain the receivedYi[n,m]in the TF domain.Finally,Yi[n,m]is transformed to theyi[k,l]in the DD domain by using SFFT.

In the case of the ideal shaping pulse,we can get the relationship between the input signalx[k,l] and the outputyi[k,l]at multicast usersUiin the DD domain,such as

where (·)Ndefines the moduloNoperator.Furthermore,lτi,pandkνi,prepresent the indices of the delay tap and Doppler tap correspond to delayτi,pand Doppler frequencyνi,prespectively by the relationship,andzi[k,l] is the complex Gaussian noise in the DD domain.Define xk=[x[k,l]···x[k,M -1]]T,andThus,the multicast message and unicast message can be denoted by vector form xM ∈CNM×1,xU ∈CNM×1.Similarly,yiand ziare constructed fromyi[k,l]andzi[k,l].The received signal yi ∈CNM×1at the multicast userUiin vectorized form can be written as

in which Hi ∈CNM×NMis the channel matrix from BS to the multicast userUi.zi ∈CNM×1is the complex Gaussian noise atUi’s end,and zi～CN

During the second phase,the signal y0and yereceived by the unicast userU0and Eve can be written as

forq ∈{0,e},where Hq ∈CNM×NMis the channel matrix from the selected DF relay to the unicast userU0and Eve,zq ∈CNM×1is the complex Gaussian noise at the unicast userU0and Eve,and zq～CN

2.3 SNR Derivation

Since Hiand Hq,forq ∈{0,e}are block cyclic matrixes,we use the frequency domain zero-forcing linear equalizer (FD-LE) approach to mitigate the intersymbol interference.Hence,after applying detection matrixto yiin Eq.(5)the received signalcan be given by

where Diis a diagonal matrix and its(kM+l+1)-th diagonal element is given by[29]

For all multicast users,the signal to interference plus noise ratio(SINR)ofxM[k,l]is given by

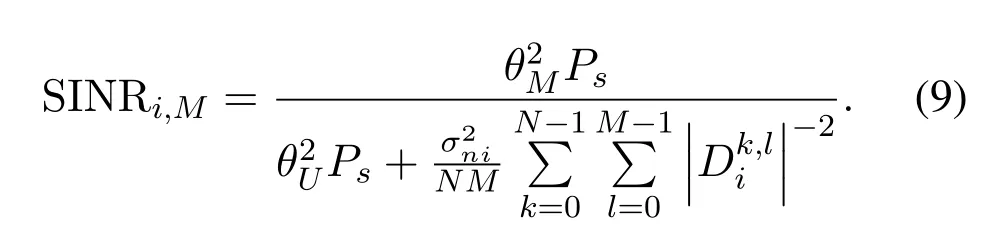
By contrast,based on NOMA scheme,the selected relay operates the successive interference cancellation(SIC) process,and the signal to noise ratio (SNR) ofxU[k,l]is given by

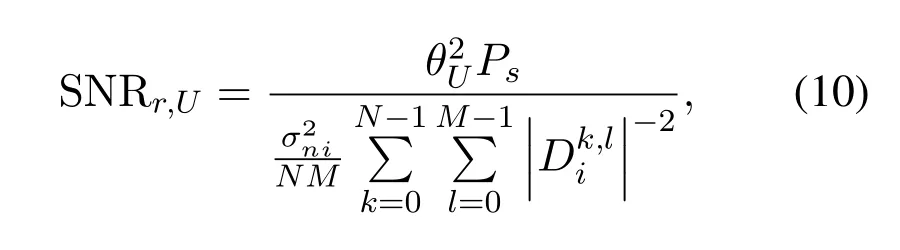
whereis the noise power of the channel from the BS to the multicast userUi.

During the second phase,the signal sent by the selected relay is potentially received by both the unicast user and Eve,and the equalized signal can be represented as

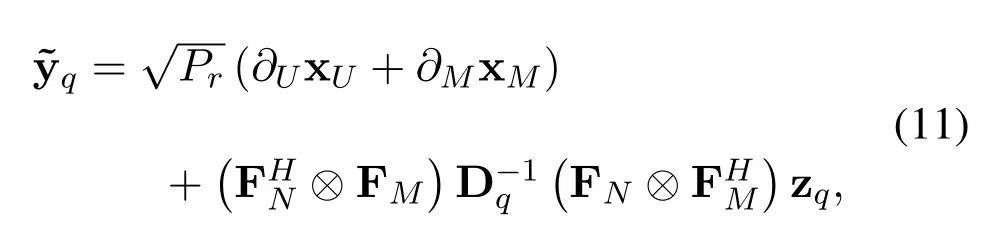
whereq ∈{0,e}corresponds to the unicast userU0and Eve respectively.

In the worse case,the eavesdropper may also carry out SIC smoothly and get the unicast signal after demodulation.As a result,the SINR and SNR of xM[k,l]andxU[k,l]in theU0and Eve’s end are given by

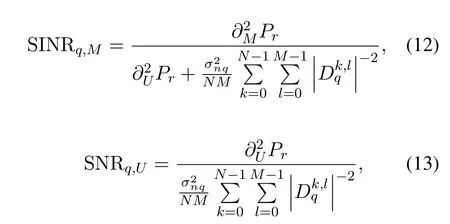
in whichq ∈{0,e},andcorrespond to the noise power of the channel from the selected relay to the unicast user and eavesdropper respectively.

III.DERIVATION OF SECURITY OUTAGE PROBABILITY

In this section,we derive the closed-form expression of SOP.Before analyzing the security transmission in the second phase,however,it is essential to discuss the power allocation in the first phase to ensure system reliable transmission.

3.1 Impact of Power Allocation

In the first phase,the transmission rate of the multicast signal is expressed asRi=log(1+SINRi,M),fori=1,2...,K,and the minimized rate is designed byRminmin{Ri,1＜i ＜K}.Therefore,making sure all multicast users demodulate the signal correctly is to guaranteeP(Rmin≥RM)≥ηholds,whereηis the given probability value used to measure the desired target rateRM,given by

whereγ(·,·) is the incomplete gamma function and.Note that,the power allocation coefficientcan be designed to achieve reliable transmission of the multicast signal in the first phase.Sinceγ(·,·) function is relatively complex,to facilitate the derivation of the power allocation condition,is approximated as[33].Hence Eq.(17)turns into

In our work,for achieving secure transmission,we assume that the relay is selected from the multicast users who can correctly demodulate the unicast signal in the first phase.This will be discussed in detail in the Subsection 4.1,where the effect of the power coefficientis also analyzed.

3.2 Derivation of Security Outage Probability

Assuming that the power allocation requirement Eq.(19)is met,let us now discuss the SOP of the unicast message.

The instantaneous secrecy capacity is defined asCs=[log(1+SNR0,U)-log(1+SNRe,U)]+,where[x]+=max{0,x}.In this case,secrecy outage occurs when the secrecy capacity is below the predefined secrecy rate,and the corresponding SOP is denoted as

In order to find the closed form of the SOP,we need to analyze the random characteristics ofZuandZe.Similar toZminin Subsection 3.1,forZu,we haveobeying inverse gamma distribution,denoted byThus we can further derive that,Zuobeys the inverse gamma distribution

Theorem 1.The SOP of unicast signal can be expressed as

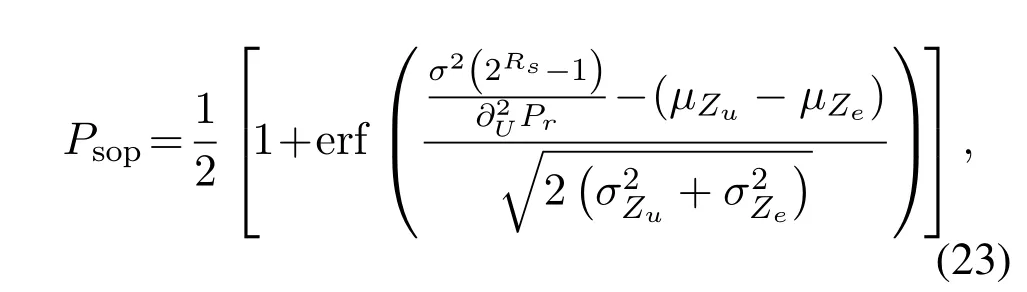
whereerf(·)is the error function with the property of monotonically increasing.

It can be seen from Eq.(23)that because of,the SOP decreases with increasing modu-lation size NM,which is related to that the OTFS system can achieve sufficient effective diversity at larger NM values.Moreover,it can also be shown from Eq.(23)that the SOP is related to the parameters of the legitimate channel and the eavesdropping channel,as well as power allocation,which will be discussed in detail in the following section.

IV.ANALYSIS OF SECURITY OUTAGE PROBABILITY

In this section,let us analyze the key factors affecting the achievable SOP of unicast.

4.1 Analysis of Power Allocation

In Subsection 3.1,the power allocation conditions have been provided to ensure that multicast users decode the signal correctly during the first phase.By contrast,let us now discuss the specific power allocation conditions for the second phase to ensure transmission security and reliability.

In the second phase,the unicast userU0also needs to correctly demodulate the multicast signal,which implies

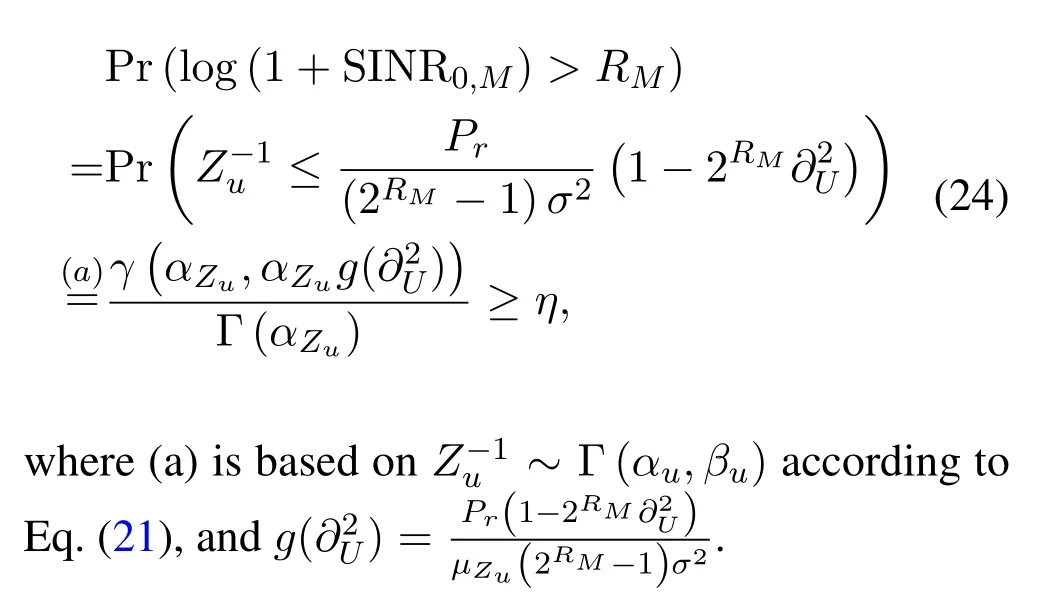
In addition,to realize the secrecy transmission of the unicast signal,i.e.SOP＜0.5 in Eq.(23),(µZu -µZe)＜0 should be met.Hence,the lower bound for Power allocation can be obtained as

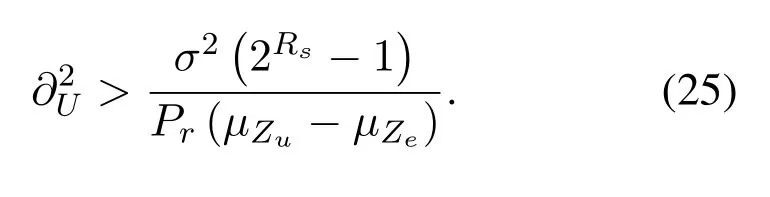
To sum up,in the following lemma we give the specific power allocation condition for the second phase.

Lemma 1.To ensure reliable reception of the multicast signal and secure transmission of the unicast signal,the power allocation coefficient during the second phase should meet the following condition

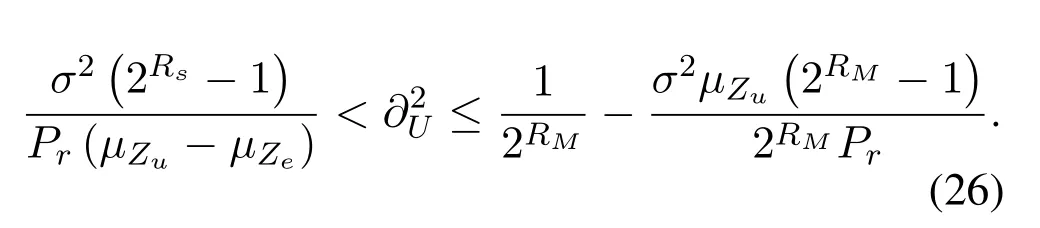
Proof.Please refer to Appendix A.

4.2 Analysis of Relay Selection

In this subsection,we analyze how the relay selection affects the SOP of unicast.

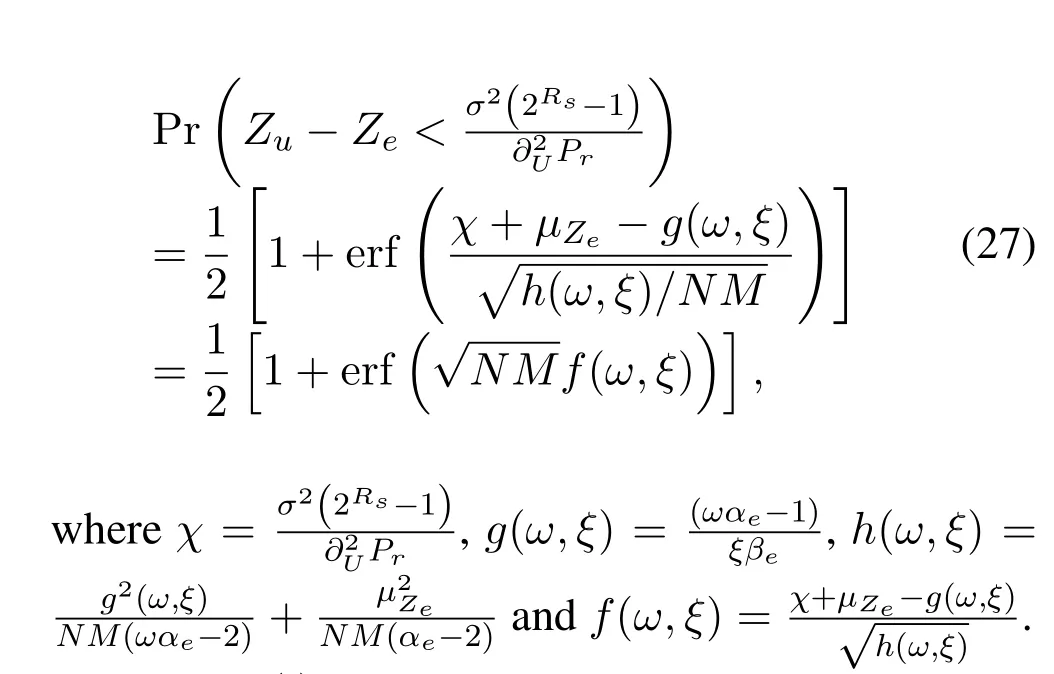
Since erf(·)function is monotonically increasing,it only needs to discuss the effects ofωandξonf(ω,ξ).In the following lemma,we summarize how the relay selection strategy affects the SOP.

Lemma 2.In order to improve the transmission security of unicast signal,the legal channel and eavesdropping channel of the selected relay should meet the following requirements

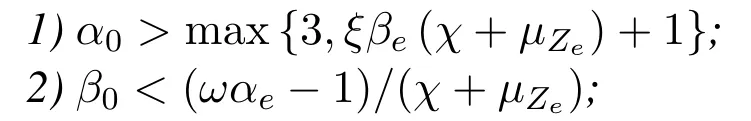
and it is also recommended to improve the security performance,i.e.to have a larger ω=α0/αe value and a smaller ξ=β0/βe value.Proof.Please refer to Appendix B.

V.SIMULATION RESULTS

In this section,simulation results are presented to verify the performance of our NOMA-OTFS based cooperative multicast-unicast system.The key parameter setup includes: the number of subcarriersMis 16,the number of OTFS symbolsNis 8,the subchannel spacing is Δf=15kHz.Further,the maximum relative velocity between BS and multicast users,corresponding to the largest Doppler shift 4.5kHz,is 450m/s with 3GHz carrier frequency.The maximum Doppler shift between the selected relay and the unicast user is 3kHz.

5.1 Impact of Power Allocation

Figure 3 provides the simulation results for OP of multicast signal with different power allocation coefficients.We consider that there are three multicast users whose channel shape parameterαand scale parameterβare 3,5,5 and 0.5,1,2,respectively.WhenRM=0.5 bits per channel use (BPCU),the upper bounds in Eq.(19) are roughly from 0.573 to 0.578 under different SNR conditions.As can be observed from Figure 3,with the decrease of,the outage probability of multicast signal is significantly reduced,thus ensuring reliable transmission and verifying the correctness of the derivations in Subsection 3.1.Besides,the transmission reliabilities of OTFS scheme and OFDM scheme are also compared in Figure 3.the OP achieved by OTFS is obviously lower than that of OFDM,especially for the scenario of OP smaller than 0.5,which corresponds to the worst case of establishing a communication link in practical systems.By contrast,we also observe that when the OP is larger than 0.5,the OTFS scheme presents a slightly worse performance than the OFDM.This is due to the fact that the OTFS scheme actually can average out the effect of various channel fading,as implied by the denominator term of Eq.(9).

In Figure 4,we illustrate the OP of the multicast signal and the SOP of the unicast signal.Let us fix SNR=10 dB and vary the power allocation coefficient.It is worth pointing out that,when,the intersection point indicates the best trade-off between the OP and SOP.Furthermore,we compare the SOP of OTFS and OFDM at.As shown in Figure 5,we find that OTFS scheme significantly outperforms OFDM,thanks to the fact that the worse channel case always plays a role in the OFDM scheme even at high transmitting power,while the OTFS scheme actually can average out the effect of various channel fading.Although the robust channel response of the OTFS scheme lead to poor security performance at a low SNR,it is meaningful only when the SOP is less than 0.5.Hence we can conclude that the security performance of the OTFS scheme is better than the OFDM counterpart in practical scenarios.Furthermore,the approximate analysis of the SOP verifies the correctness of Theorem 1.

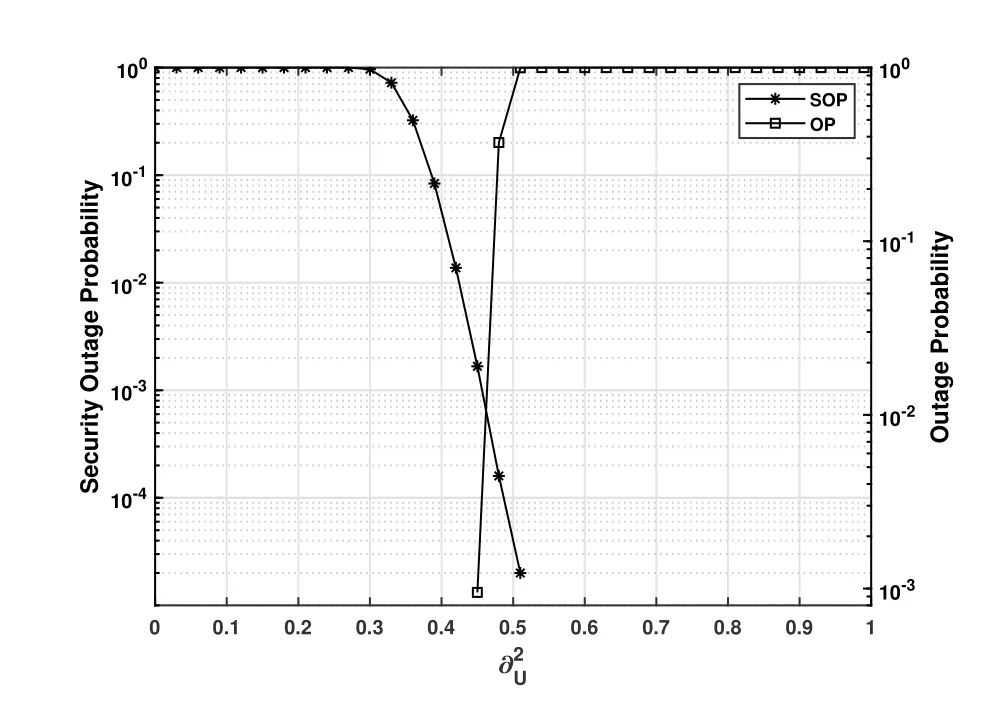
Figure 4. The variation of SOP and OP with in the second phase.

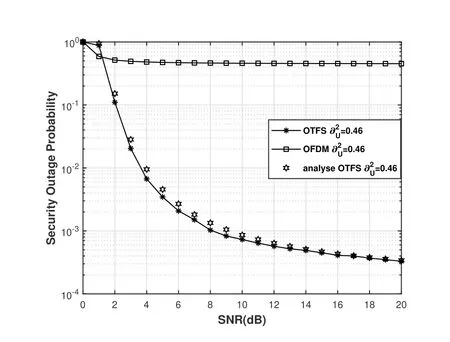
Figure 5. SOP comparison for OTFS with OFDM scheme.

5.2 Impact of Relay Selection

We consider the case that the optimal allocation coefficient=0.46 is used.In Figure 6,we set the legitimate channel and eavesdropping channel parameters areα0=5ω,αe=5,andβ0=βe=1;(ξβe(χ+µZe)+1)in Lemma 2 is about 6.19 to 6.65 at different transmitting powers,Figure 6 verifies that whenωis correspondingly greater than the range 1.24 to 1.33 at different transmitting SNRs,the greater the ratio of the shape parameters between the legitimate channel and the eavesdropping channel,the better the security of the unicast signal.

Figure 6. SOP performance of OTFS scheme under different channel shape parameters.

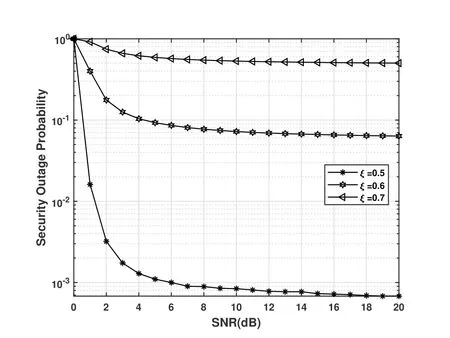
Figure 7. SOP performance of OTFS scheme under different channel scale parameters.

In Figure 7,we set the legitimate channel and eavesdropping channel parameters asα0=αe=5 andβ0=ξβe=ξ,respectively.Furthermore,in Lemma 2,(ωαe-1)/(χ+µZe) is about 0.71 to 0.78 at different transmitting powers.Figure 7 shows that,whenξis correspondingly lower than the range 0.71 to 0.78 at different transmitting SNRs,the ratio of the scale parameters between the legitimate channel and the eavesdropping channel gets smaller,i.e.the greater the difference in channel quality,and the security of the unicast signal can be enhanced.

VI.CONCLUSION

In this paper,we have developed the NOMA-OTFS assisted cooperative multicast-unicast streaming.We have derived the power allocation condition to ensure the reliable transmission of the multicast signal.Furthermore,we have introduced the relay selection scheme to improve the security of unicast streaming.Our simulation results have shown that the use of the NOMA-OTFS assisted multicast-unicast transmission can yield a significant improvement in reliability and security compared to the existing NOMA-OFDM schemes.In addition,the secrecy of the unicast signal can be enhanced by improving the quality of legitimate channels,guided by relay selection requirements.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China(No.61941105,No.61901327 and No.62101450),in part by the National Natural Science Foundation for Distinguished Young Scholar (No.61825104),in part by the Fundamental Research Funds for the Central Universities(JB210109),in part by the Foundation of State Key Laboratory of Integrated Services Networks of Xidian University(ISN22-03).

APPENDIX

A Proof of Lemma 1

Here we analyze the power allocation coefficient in the second phase.Considerη=0.5,Eq.(24)can be further written as

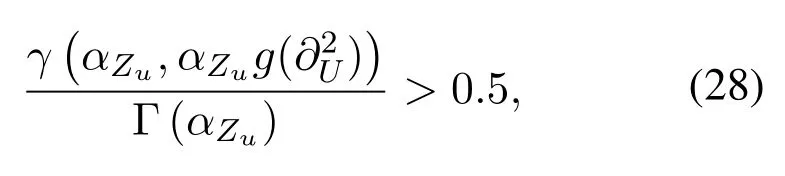
and Eq.(28) can be further expressed asf(x,y)=,where the independent variablesxandyare used to refer toandαZu,respectively.

whenx=1,is a decreasing function ofy.Thus the value off(y) is the lower bound asygoes to infinity.According to [34],wheny →∞,we have Γ(y,y)～yy-1e-y,and wheny ＞1,we have

B Proof of Lemma 2

Firstly,take the derivative off(ω,ξ)with respect toω,we can get

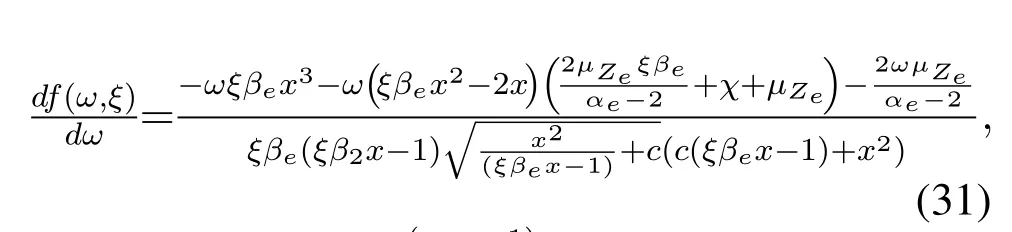
Secondly,take the derivative off(ω,ξ)with respect toξ,we can get

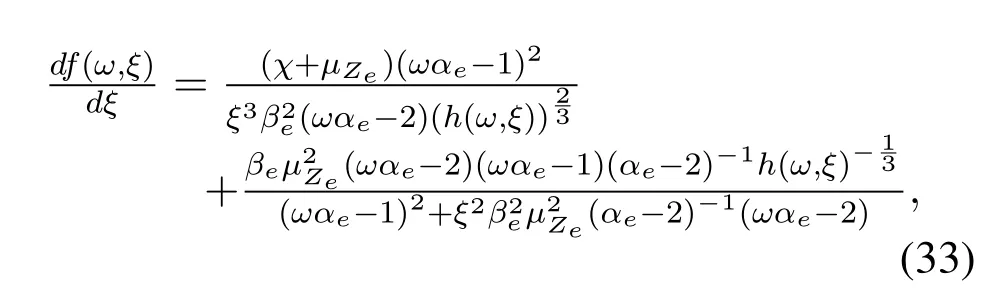
whereωαe-2=α0-2＞0,αe-2＞0 andh(ω,ξ)＞0,thus as can be seen from,the SOP decreases with the decrease ofξ.Besides,similarly according to Eq.(25),β0＜(ωαe-1)/(χ+µZe) is guaranteed to make sure SOP is less than 0.5.