Iterative Receiver for Orthogonal Time Frequency Space with Index Modulation via Structured Prior-Based Hybrid Beliefand Expectation Propagation

Haoyang Li ,Bin Li ,Tingting Zhang,* ,Yuan Feng ,Nan Wu

1 School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China

2 China Research and Development Academy of Machinery Equipment,Beijing 100089,China

Abstract: Orthogonal Time Frequency Space(OTFS)signaling with index modulation (IM) is a promising transmission scheme characterized by high transmission efficiency for high mobility scenarios.In this paper,we study the receiver for coded OTFS-IM system.First,we construct the corresponding factor graph,on which the structured prior incorporating activation pattern constraint and channel coding is devised.Then we develop a iterative receiver via structured prior-based hybrid belief propagation (BP) and expectation propagation(EP)algorithm,named as Str-BP-EP,for the coded OTFS-IM system.To reduce the computational complexity of discrete distribution introduced by structured prior,Gaussian approximation conducted by EP is adopted.To further reduce the complexity,we derive two variations of the proposed algorithm by using some approximations.Simulation results validate the superior performance of the proposed algorithm.

Keywords: OTFS;index modulation;message passing;belief propagation;expectation propagation

I.INTRODUCTION

With the advent of the sixth generation (6G) era,high speed and ultra-reliable communications in high mobility scenarios,including online gaming,vehicleto-everything (V2X),and low-earth-orbit satellites(LEOs),has been receiving tremendous attention.The widely adopted orthogonal frequency division multiplexing (OFDM) modulation scheme in the current fifth generation (5G) networks suffers performance degradation in the presence of Doppler shift induced by high mobility.Recently,a two-dimensional (2D)modulation scheme referred to as orthogonal time frequency space (OTFS) was proposed,where the information symbols are multiplexed in the delay-Doppler domain rather than the time-frequency domain [1,2].OTFS modulation,which converts the time-varying channel in time-frequency domain into a quasi-static channel in delay-Doppler domain,is a promising modulation technique for high mobility scenarios [3,4].In [5],a practical transmit diversity scheme for OTFS system with multiple antennas was proposed to achieve spatial diversity.Moreover,OTFS combined with massive multiple-input multiple-output(MIMO)technique is a powerful candidate for realizing integrated sensing and communication(ISAC)[6].

Since only a few reflectors are involved in the signal propagation,the delay-Doppler domain representation of the channel is sparse,which significantly reduces the complexity of receiver [7].In [8],a low-complexity detection algorithm based on mean field approximation for OTFS system was proposed,in which the global optimal solution can be obtained efficiently by choosing the approximate distribution.In [9],a novel cross domain iterative detection algorithm was proposed to enhance the error performance of OTFS modulation,where the detection is performed in time-frequency domain and delay-Doppler domain iteratively.At the transmitter side,to further improve the data detection performance,[10] proposed an optimal transmitter window design approach to minimize the detection mean square error by a water-filling power allocation scheme.

Index modulation has been developed to improve both the spectral efficiency and energy efficiency[11,12].Owing to the introduction of index domain,more information can be transmitted with the same transmission power.A scheme adopting dual-mode index modulation (DM-IM) was proposed for OTFS to achieve a better trade-off between the transmission reliability and spectral efficiency [13].In [14],an inphase and quadrature index modulation scheme (IQIM),was presented to increase the spectral efficiency of OTFS,in which additional information bits are carried through the grid index of OTFS frame in in-phase and quadrature dimensions.By exploiting the degrees of freedom in the spatial domain,a spatial modulation(SM) based OTFS system was devised to further enhance the spectral efficiency[15].

Nevertheless,The introduction of index domain in OTFS makes the design of receiver becomes more complicated.Most existing researches on the design of OTFS-IM receiver adopt minimum mean square error (MMSE) and message passing algorithms to design equalizer,followed by a maximum likelihood(ML)based IM detector.However,these schemes fail to incorporate the prior of IM into equalization,resulting in performance degradation.To deal with the prior of IM,a hybrid belief propagation (BP) and expectation propagation (EP) based algorithm was proposed for Faster-than-Nyquist-IM(FTN-IM)system[16],in which the activation pattern constraint is neglected.An approximate message passing (AMP) based algorithm using structured but uniform prior was proposed for spatial modulation system[17,18],which does not fully exploit the channel coding gain.

In this paper,we propose a structured prior-based hybrid BP and EP algorithm,named as Str-BP-EP,to design iterative receiver for coded OTFS-IM system,in which the information of IM and channel coding is incorporated inherently by the devised structured prior.Then two variations of the proposed algorithm are derived.We would like to remark that the proposed algorithms are also applicable to the uncoded OTFSIM system by assuming the uniform bit prior.Simulation results validate the superiority of our proposed algorithms in both coded and uncoded settings.The main contributions of this paper can be summarized as follows:

• We derive the factorization of posterior probability for the coded OTFS-IM system and construct corresponding factor graph,on which structured nodes are introduced to incorporate the activation pattern constraint and channel coding.Accordingly,a structured prior is devised.By exploiting the sparsity of channel matrix in delay-Doppler domain,we proposed a low-complexity hybrid BP and EP algorithm based on the devised structured prior.Gaussian approximation conducted by EP is adopted to reduce the computational complexity of discrete distribution introduced by structured prior.

• To further reduce the computational complexity,we derive two variations of the proposed algorithm,namely,simplified BP-EP and Str-AMP.Specifically,we first use the approximate unstructured prior to derive the simplified BP-EP.Then the first-order approximation to the messages on factor graph is adopted to derive the Str-AMP.

Notations: We use normal-face letters to denote scalars,lowercase (uppercase) boldface letters to denote column vectors (matrices).The (m,n) element of a matrix X is denoted as Xm,n.The superscripts(·)Tand (·)Hrepresent the transpose and Hermitian transpose operators,respectively,while⊗denotes the Kronecker product operator;vec(·) denotes the vectorization from a matrix of sizeM ×Nto a vector,and unvecM,N(·) is the inverse operation of it;FNand IMdenote the discrete Fourier transform (DFT)matrix of sizeN ×Nand the identity matrix of sizeM×M,respectively;denotes the complex Gaussian distribution of a random variable with meanµand varianceσ2,and Ep[·] denotes statistical expectation operator with respect to distributionp;C(n,k)denotes the binomial coefficient;δ(·)denotes the Dirac delta function,anddenotes the floor function.

II.OTFS-IM SYSTEM MODEL

Considering LDPC code and IM technique employed in delay-Doppler domain,the structure of LDPCcoded OTFS-IM transceiver is depicted in Figure 1.The coded bit stream from LDPC encoder,which is specified by a parity-check matrix with low-density structure,is partitioned intoGblocks,each of which containsLbits.Then,every block is partitioned into two sub-blocks withLAPandLSbits each,respec-Letdenotes tively referred to as index bits and information bits.the bit vector of theg-th block.The firstLAP=log2C(NG,NA)」bits are invoked by the index selector to determineNAactive resource elements(REs)out ofNGREs,while the other REs are kept silent in the current transmission duration.Note thatLAPbits can only support up toQ=2LAPmapping patterns from index bits to active REs,referred to as activation pattern constraint.Define A={a1,...,aQ}with aq=[aq,1,...,aq,NG]T∈{0,1}NGas the set of activation patterns,where‖aq‖0=NA,aq,n=1 if thei-th RE is activated,andaq,n=0 otherwise.The followingLAP=NAlog2Mbits are used to selectNAsymbols from the modulation alphabet S={s1,...,sM},which will be placed in the legitimate activation positions.Therefore,after IM,cgis mapped to a vector xgwithNAnonzero entries drawn from S.

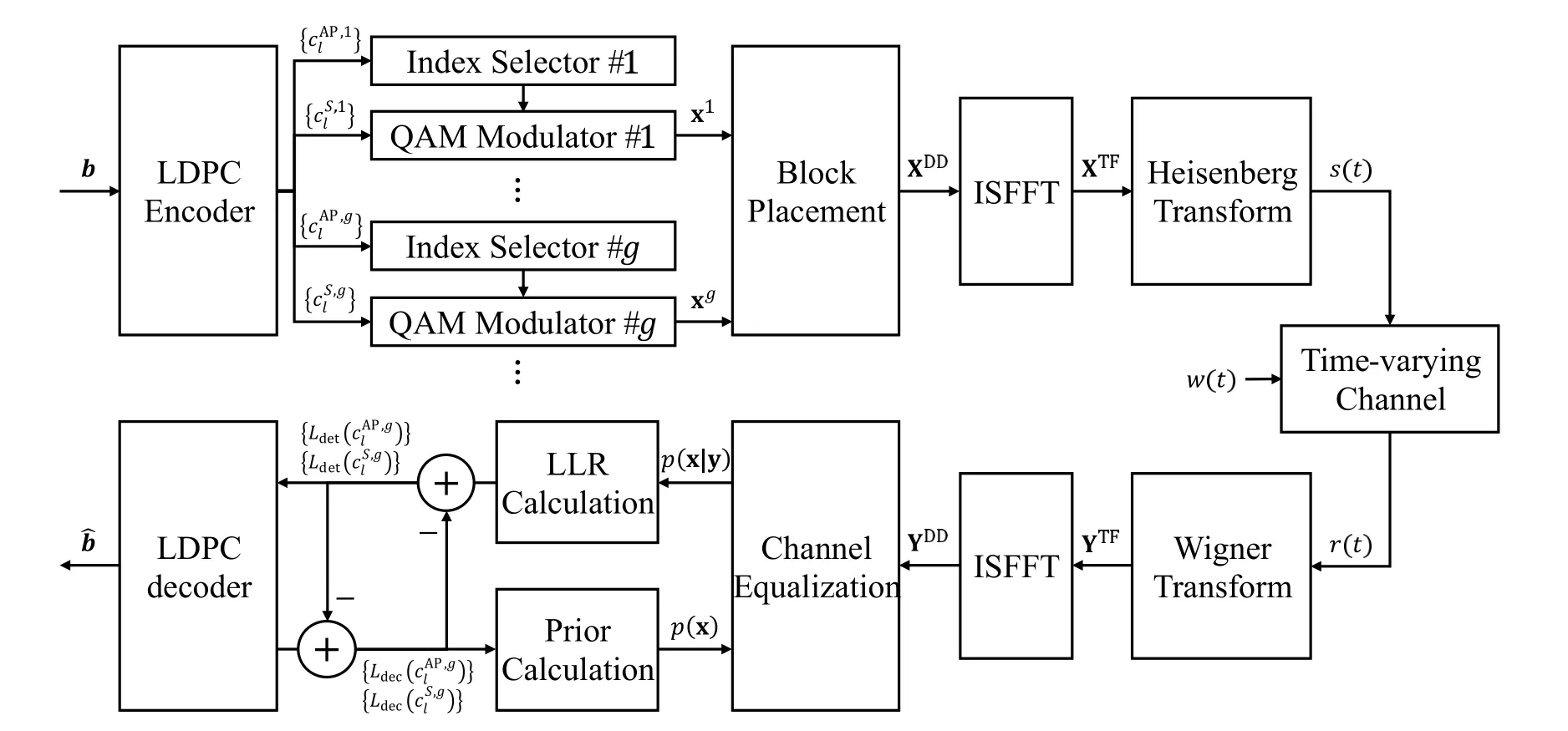
Figure 1. Transceiver structure of the LDPC-coded OTFS-IM system.

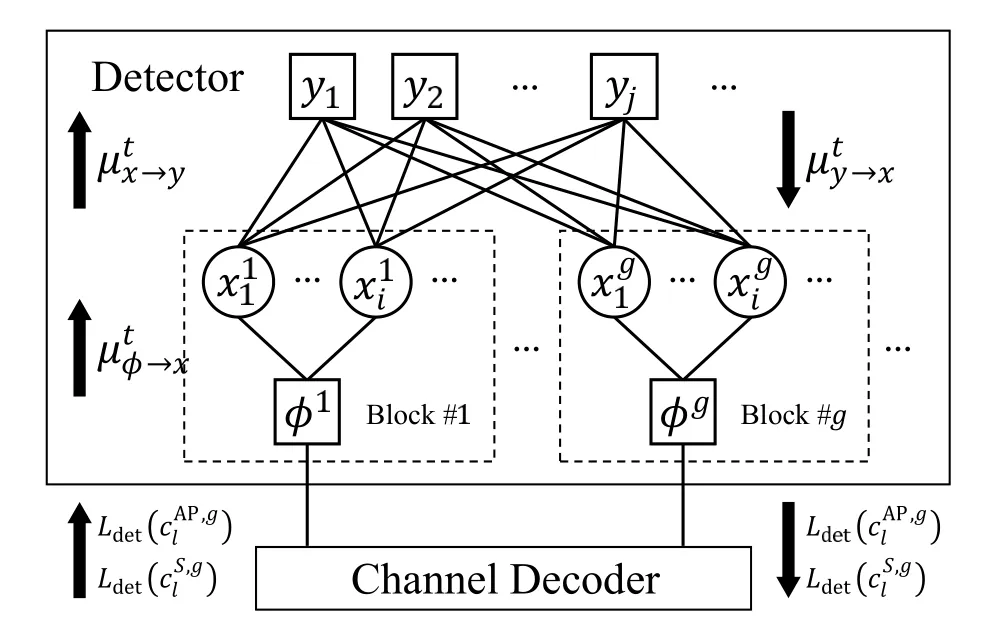
Figure 2. Factor graph representation of the iterative receiver for coded OTFS-IM system.

The OTFS signaling is conducted by a cascade of two 2D transforms at both the transmitter and receiver.Suppose a signal frame has durationNDToccupying a bandwidthMDΔf,whereTΔf=1.Hence,there areNRE=MDNDresource elements(REs)in a transmission duration.First,theinverse symplectic finite Fourier transform(ISFFT)maps the information symbols XDD∈CMD×NDin the delay-Doppler domain to symbols XTF∈CMD×NDin the time-frequency domain,i.e.,

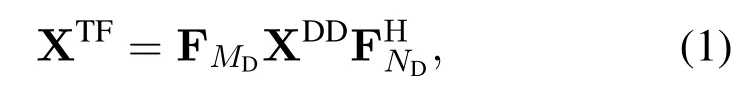
where XDDis the arrangement of{xg}.Then,theHeisenberg transformuses anMD-point IFFT along with pulse-shaping waveformgtx(t) to generate the time domain signals(t)by

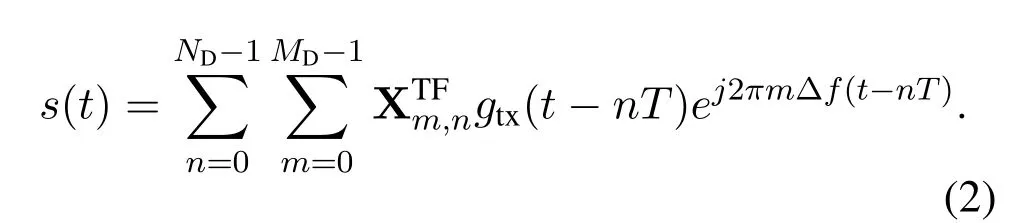
The vector representation of(2)can be written as[19]

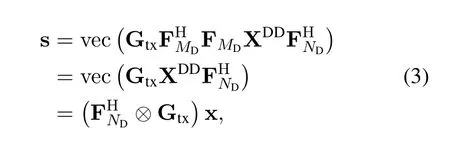
where Gtxis a diagonal matrix with entries sampled()fromgtx(t),and.By placing{xg}along with the delay grid,Then,one CP is added for the entire OTFS frame to eliminate inter frame interference.

Given the time-varying channel with baseband channel impulse responseh(τ,ν),which characterizes the channel response to an impulse with delay and Doppler[20],the received signalr(t)is given by

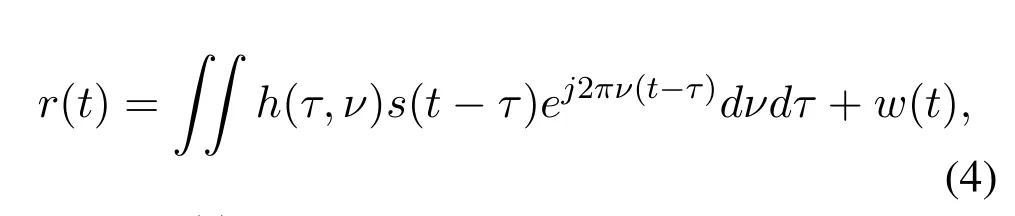
wherew(t) is the additive white Gaussian noise(AWGN) with power spectral densityσ2at the receiver.Since typically there is only a small number of reflectors in the channel with associated delays and Doppler shifts,the channel impulse responseh(τ,ν)can be expressed via a sparse representation,i.e.,

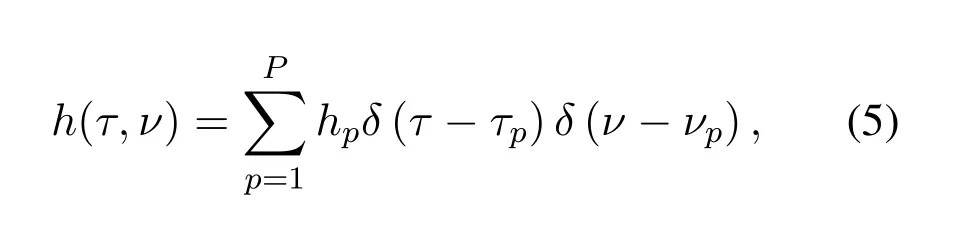
wherePis the number of propagation paths,andhp,τp,andνpdenote the complex path gain,delay,and Doppler shift associated with thep-th path,respectively.We denote the delay and Doppler shift taps for thep-th path asτp=mp/(MDΔf) andνp=np/(NDT),respectively,wheremp ＜MDandnp ＜ND,i.e.,the channel is underspread.We assume that the delay and Doppler shift taps lies on the delay-Doppler grid,i.e.,mpandnpare integers.Accordingly,after discarding the CP,vector representation of the received signal in(4)is given by

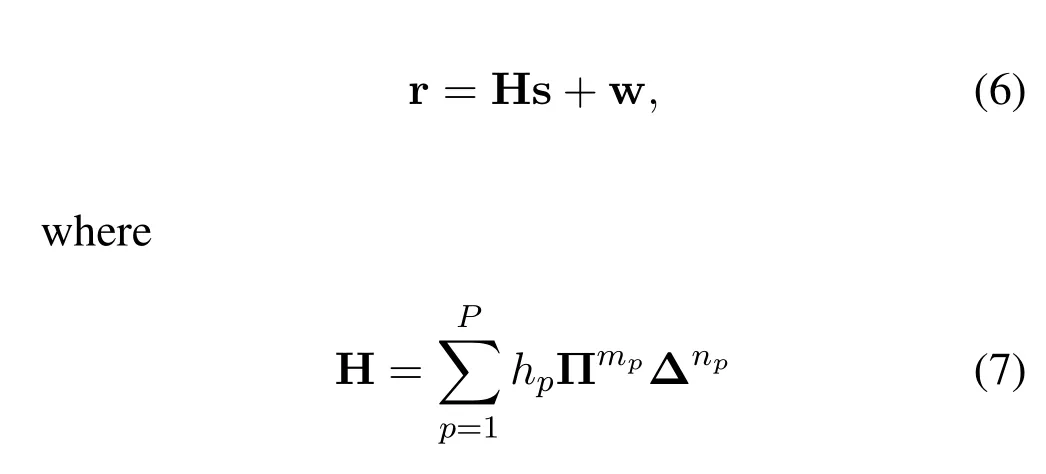
is aNRE×NREmatrix with Π and Δ modeling the delays and Doppler shifts in(4),respectively,and w～CNis the AWGN.Specifically,Π is a cyclic shift matrix,and Δ is a phase rotation matrix[7].Then,theWigner transformis employed,i.e.,

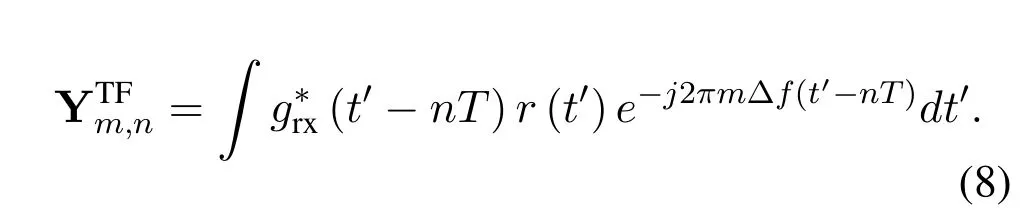
Rewriting(8)in matrix form,we have

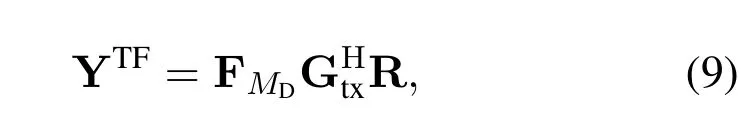
where R=unvecMD,ND(r),and Grxis a diagonal matrix with entries sampled fromgrx(t).By adoptingsymplectic finite Fourier transform(SFFT),the received signal in the delay-Doppler domain is given by

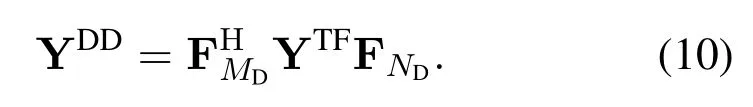
Similar to(3),we can rewritten(10)as

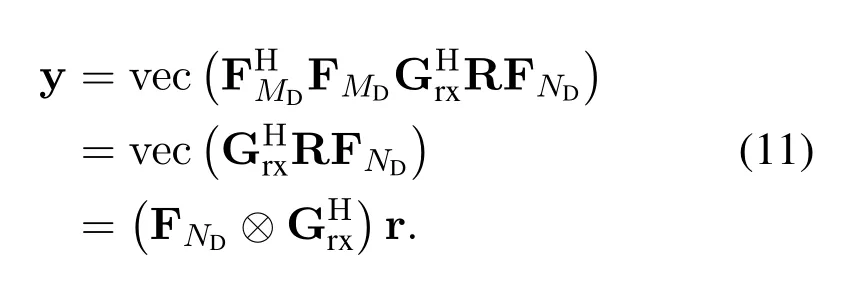
Substituting(3)and(6)into(11)and adopting the rectangular window,i.e.Gtx=Grx=IMD,the system model can be summarized as

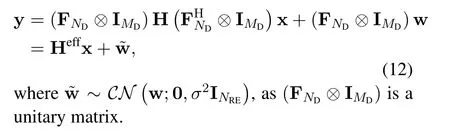
Due to the sparsity of the time-varying channel in delay-Doppler domain,the effective channel matrix is also sparse.Specifically,there are onlyPnonzero elements in each row or column of Heff.

After obtaining the sufficient statistic y,channel equalization and LDPC decoder are employed to recover the information bits.By exchanging extrinsic information iteratively,which can be interpreted as successive interference cancellation in a soft manner,the receiver can exploit the channel coding gain by turbo equalization and achieve better error performance[21].

III.STR-BP-EP BASED ITERATIVE RECEIVER FOR LDPC-CODED OTFS-IM SYSTEM

3.1 Graphical Model of Coded OTFS-IM System

Factor graph is a kind of bipartite graph which represents the factorization of probability.Based on the received signal model in(12),the factorization of posterior probabilityp(x|y)is given by

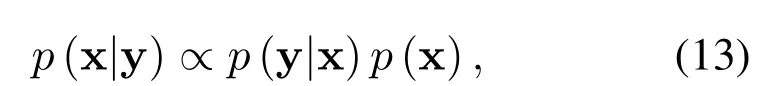
where the likelihood functionp(y|x)can be fully factorized as

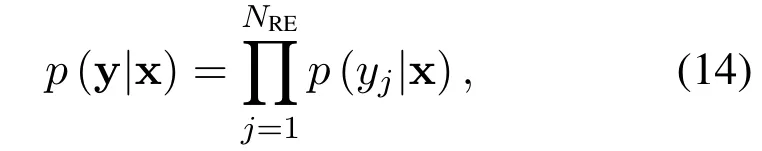
To this end,we devise a structured prior that incorporates the activation pattern constraint and channel coding.Accordingly,p(x)can be written as

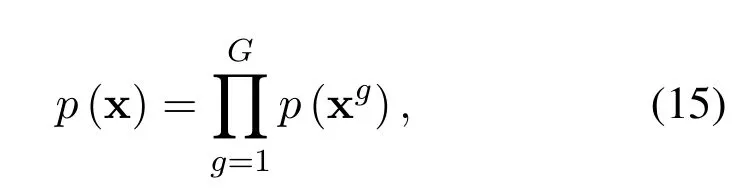
where the structured priorp(xg)is given by(16).

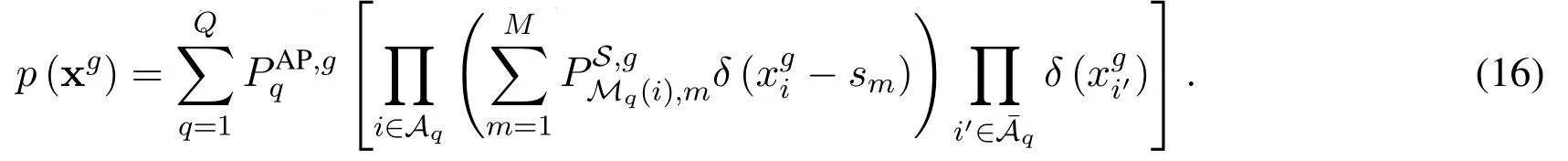
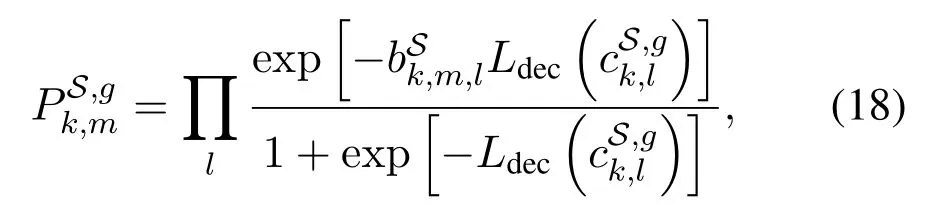
According to the factorization of posterior probability in (13)-(15),factor graph model of iterative receiver for the coded OTFS-IM systems is illustrated in Figure 2.The variable nodecorresponds to the symbol to be inferred.The observation nodeyjcorresponds to the likelihood factorp(yj|x).Variable nodehas connection to observation nodeyjif and only ifis a variable ofp(yj|x),i.e.,hj,(g-1)NG+10.The structured nodeϕgconnected tocorresponds to the prior factorp(xg),which satisfies the activation pattern constraint.The factor nodes utilize the observations and extrinsic LLRs from decoder to compute the messagesto the variable nodes,respectively,and update their information by aggregating these messages at the variable nodes,which results in the messageBased on different criteria,we can derive corresponding message updating rules,leading to different message passing algorithms.In the following part,we will employ BP and EP to derive the message passing algorithm based on the structured prior.

3.2 Structured Prior-based Hybrid Belief and Expectation Propagation

Since the maximuma posteriori(MAP)algorithm for optimal equalization and decoding is generally not tractable,we employ the concept of turbo equalization to design the iterative receiver for coded OTFSIM system by exchanging LLRs between the detector and decoder [21,23].For detector,the optimal MAP equalization is achieved by maximizing the marginal posterior probability of transmitted symbols.However,the direct calculation on original distributionp(x|y) is also intractable,and approximate methods have to be employed.

Variational inference(VI)is a powerful approach to efficiently calculate the marginal probability[24,25].The key idea of VI is to choose a simple distributionq(x|y) to approximate the target posterior distributionp(x|y) by optimizing some metric,e.g.,Kullback-Leibler (KL) divergence.In fact,there are two types of approximate message passing algorithms from the perspective of VI by optimizing the inclusive KL divergence and exclusive KL divergence[26],respectively.The well-known BP Algorithm [27,28],which is an effective approach for probability inference on factor graph by passing the message between the variable nodes and factor nodes iteratively,can be derived from minimizing exclusive divergence KL(q(x|y)|p(x|y))[29].

For simplicity,andx(g-1)NG+iarebothused to indicate the same transmitted symbol on thei-th RE in theg-th block,and so do its parameters.Letbe the message from the variable nodexito the observation nodeyj,and letbe the message in the opposite direction.The message from the structured nodeϕgto the variable nodeis denoted as

The message updating rules of BP[27]are given by

Obviously,it would be computationally intensive to calculateusing Gaussian approximation directly,which is on an order of.To this end,we using EP to efficiently reduce the computational complexity[31].To calculate the symbol belief,we substitute(21)into(19),and multiply both side by,i.e.

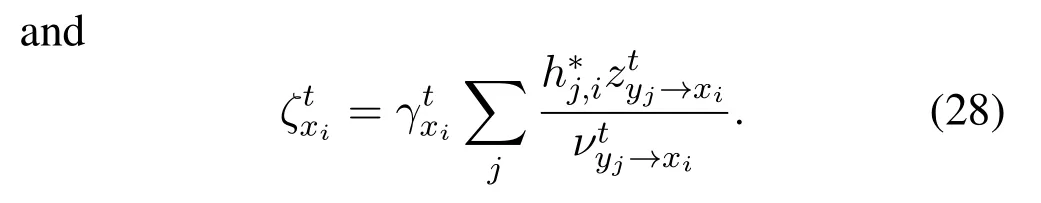
Substituting(16)into(26),we can get the belief of,given by(29)and(30).

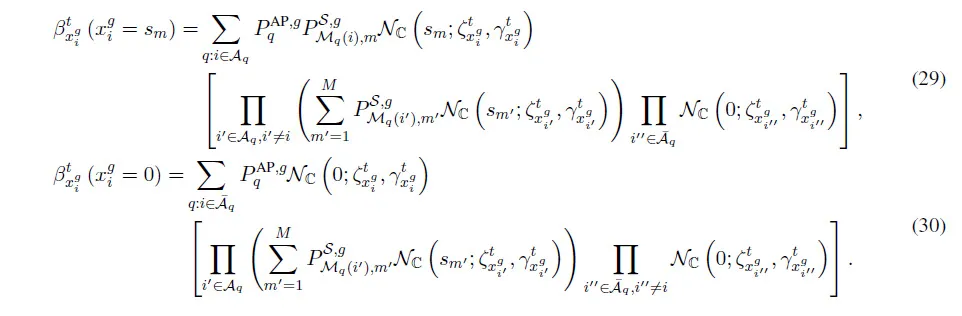
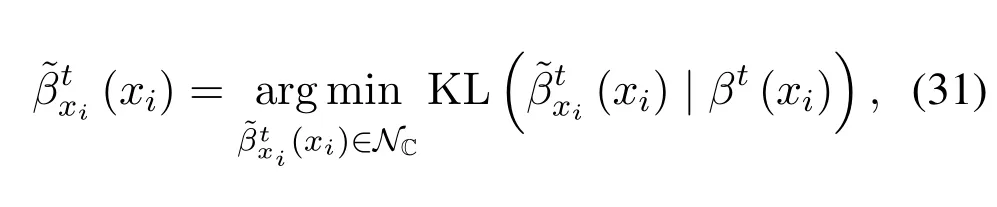
where the mean and variance of the approximate Gaussian distribution(xi)is given by

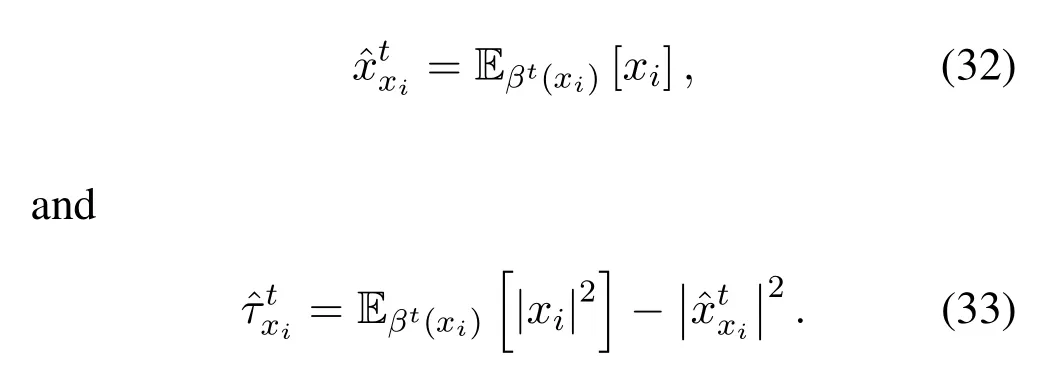
According to the properties of Gaussian function division,we have

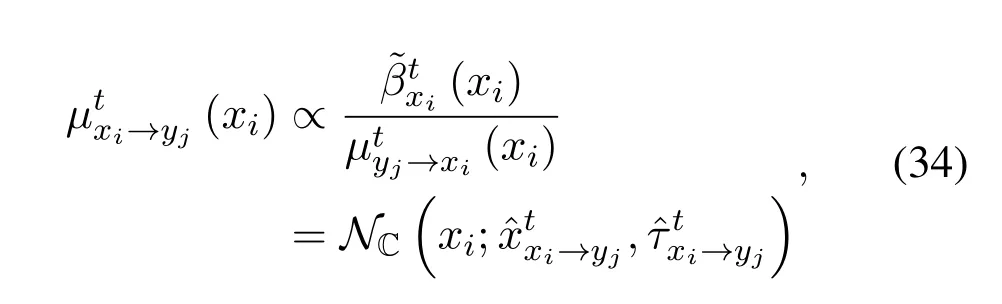
where the mean and variance ofis given by

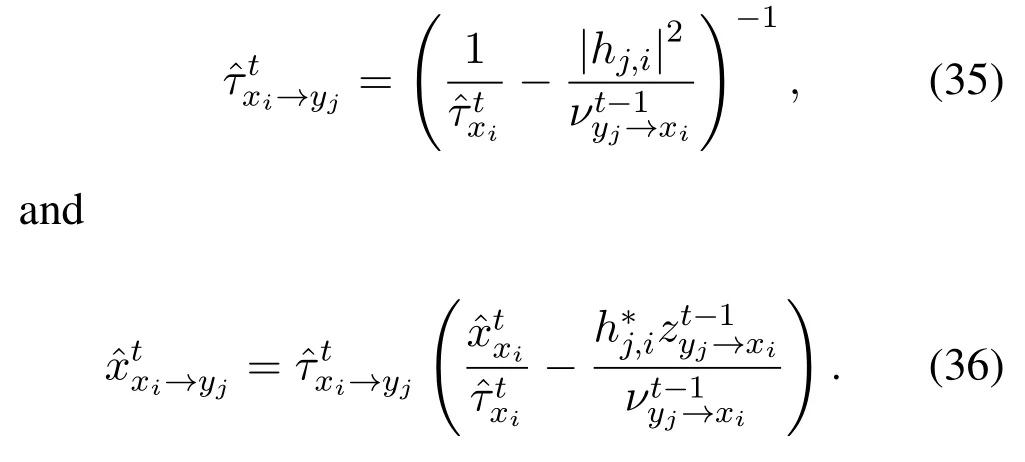
We can see that the computational complexity of Gaussian approximation is reduced toO(NRE).After several iterations,the marginal posterior distribution of xgcan be calculated by

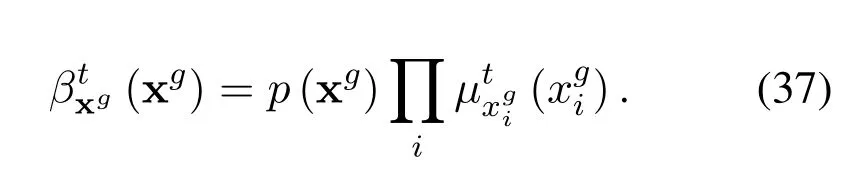
Since the proposed Str-BP-EP is a soft detection algorithm,we can carry out the LLR of each bit,including,both the index bits and information bits.Given(xg),the extrinsic LLR for thel-th index bits in theg-th block is given by

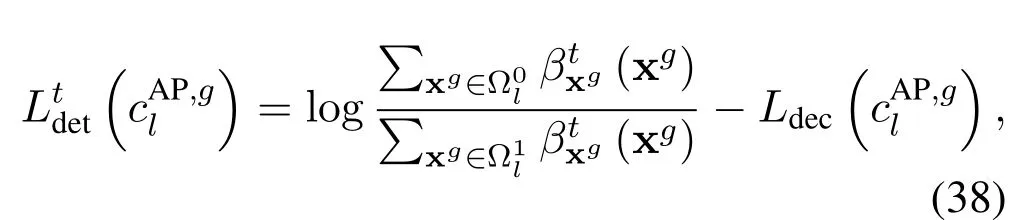
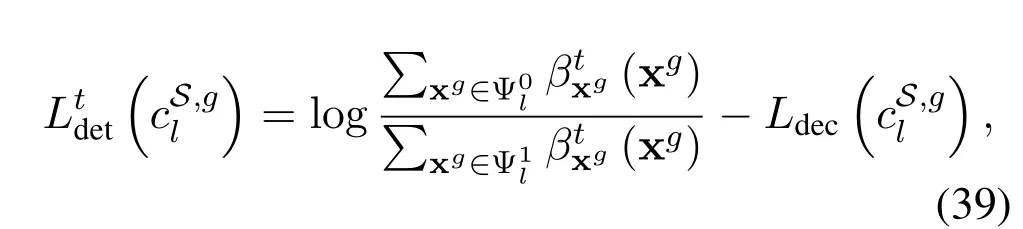
To efficiently exploit the channel coding gain,the LLRs from the detector are sent to the decoder once it is updated,i.e.,there is only one inner iteration within the detector.We summarize the proposed Str-BP-EP algorithm in algorithm 1,in which only one iteration is performed for convenience.

3.3 Variations of the Proposed Algorithm

To further reduce the computational complexity,we derive two variations of the proposed algorithm,namely,simplified BP-EP and Str-AMP,by using some approximations.

We first derive the simplified BP-EP algorithm using the approximate unstructured prior.The local factor graph of BP-EP is shown in Figure 3,in which the prior is fully factorized,approximately,i.e.,

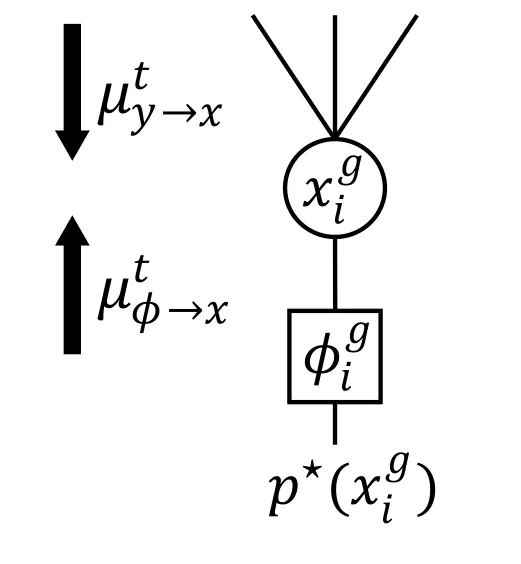
Figure 3. Local factor graph representation of BP-EP.

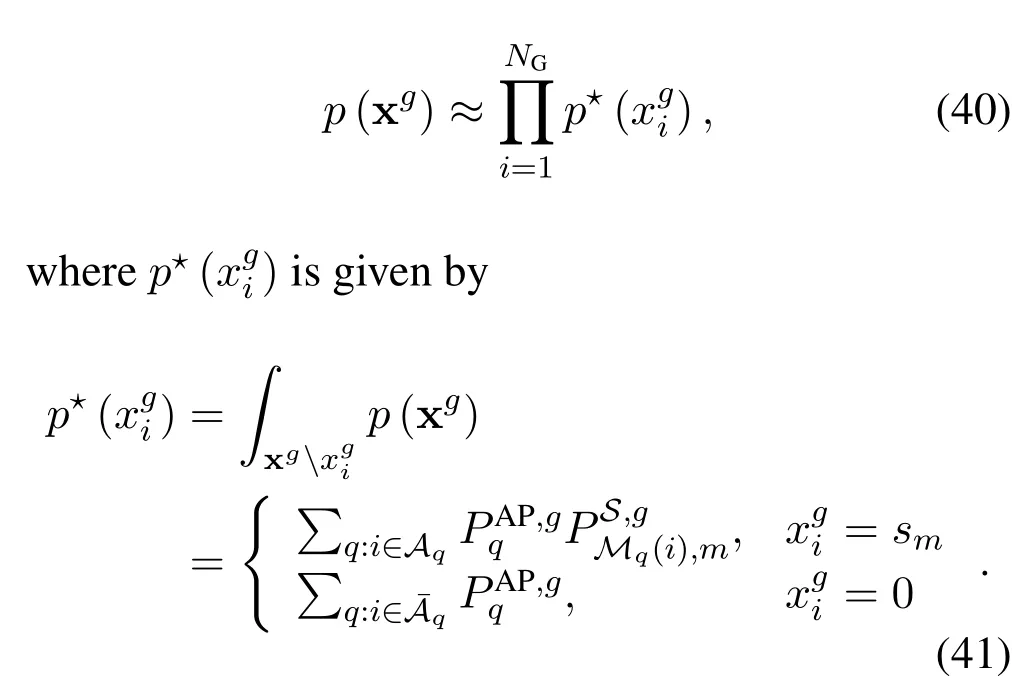
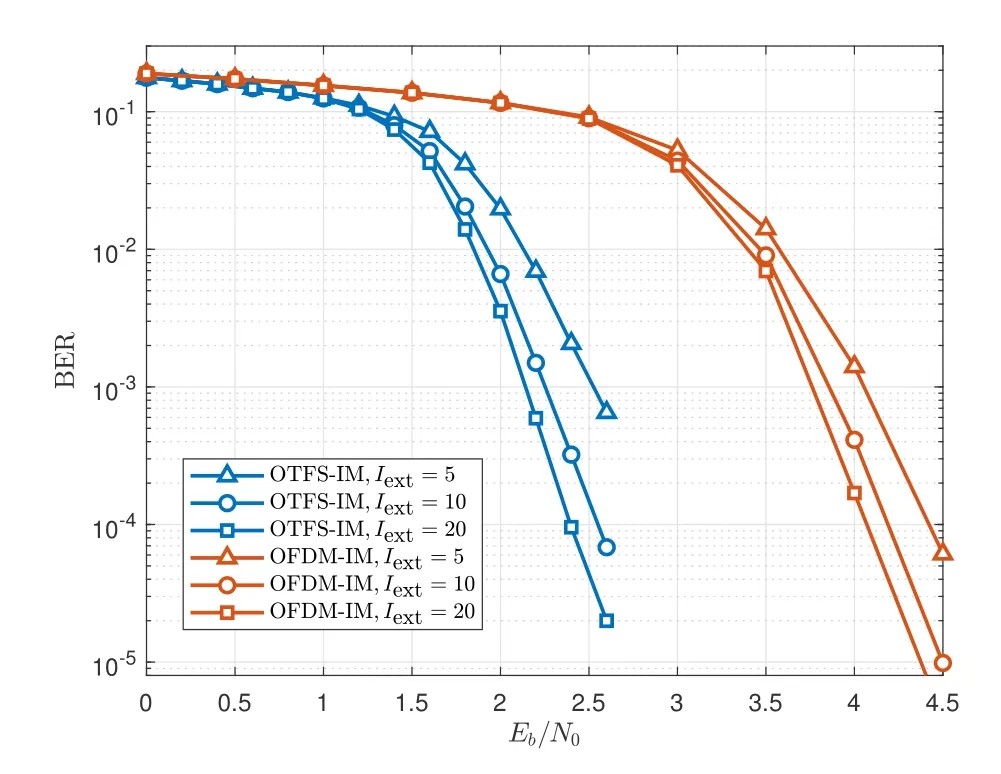
Figure 4. BER performance of the proposed Str-BP-EP based receiver in OTFS-IM and OFDM-IM systems with mode(4,1,4).

The derivation of simplified BP-EP is similar to Str-BP-EP except that the belief in (29) and (30) is replaced by(42).

Hence(27)and(36)can be approximated by

By using the first-order approximation,(24)can be approximated by

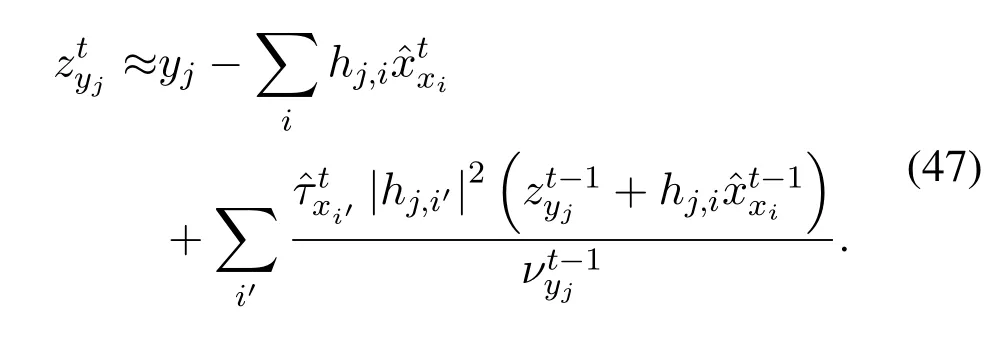
Likewise,(28)can be approximated by

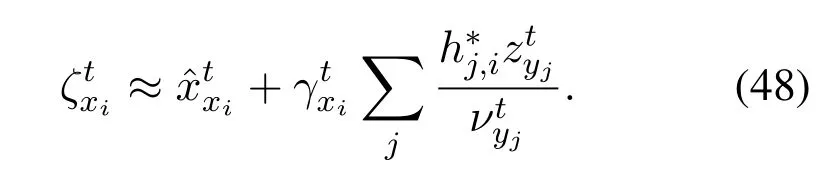
The derivations of (47) and (48) are given in the Appendix.After approximation,we can remove the mes-sagesin Str-BP-EP.So far,we obtain the Str-AMP from Str-BP-EP by computingwith (45),(47) and (48),respectively.

3.4 Complexity Analysis

It is noted that since the effective channel matrix Heffis sparse,the factor graph is partially connected with only a few edges connecting to a node.Therefore,the number of messages updating on factor graph is limited,making the proposed Str-BP-EP algorithm practical to implement.The complexity of one iteration involves the computation of each massage passing on factor graph.Since the exponential operation is usually implemented by a look-up table and the complexity of addition operation is negligible compared with that of multiplication,the computational complexity of message updating is dominated by the number of complex multiplication.To compare the complexity explicitly,we only consider the number of multiplication operation.

For Str-BP-EP,the complexity of computingis on the order of.The complexity of BP and EP is on the order ofO(PNRE)andO(MNRE),respectively.Therefore,the total computational complexity of Str-BP-EP is on the order ofO(NRE(MNA+MQNG+P)).Similarly,the total computational complexity of simplified BP-EP is on the order ofO(NRE(MQ+P)),and the total computational complexity of Str-AMP is on the order ofO(NRE(MNA+MQNG+P)).Despite the same complexity order,the actual computational complexity of Str-AMP is less than that of Str-BP-EP due to some approximations.As a comparison,the softin-soft-out MMSE-based(SISO MMSE)equalization in[33]has a complexity on the order ofowing to the matrix inversion.The complexity order of various algorithms are briefly summarized in Table 1.

Table 1. Summary of complexity of various algorithms.

IV.SIMULATION RESULTS

We evaluate the bit error rate (BER) performance of the proposed algorithm for coded OTFS-IM system.In the following simulations,we employ a LDPC code with rater=1440/2016.In one OTFS frame,there areMD=48 subcarries andND=42 time slots,henceNRE=2016.The parameter of IM mode is indicated by(NG,NA,M).Two common IM modes,i.e.,(4,1,4) and (4,2,2),of the same spectral efficiency 1 bps/Hz are evaluated using our proposed algorithms.The carrier frequency is 5 GHz and the subcarrier spacing is 7 kHz.The relative speed of the receiver isv=144 km/h,leading to a maximum Doppler shift indexnmax=4,and the maximum delay index ismmax=4.We consider a channel withP=4 propagation paths,where the taps of delay and Doppler shift are fixed,and the total power of all paths is normalized.We assume the perfect channel state information at the receiver.For turbo equalization,the maximum number of LDPC decoding is 10,and we useIextto indicate the number of turbo iterations.

In Figure 4,we evaluate the BER performance of the proposed Str-BP-EP based receiver for OTFS-IM systems with mode(4,1,4).The OFDM-IM counterpart is also studied for comparison.We can observe that OTFS-IM outperforms OFDM-IM by over 1.5dB at BER of 10-4,demonstrating the advantages of OTFSIM system against time-varying channel induced by high mobility.Besides,the BER performances of Str-BP-EP based receiver can be improved by increasing the number of iterations.Nevertheless,the performance improvement becomes marginal whenIextincreases.

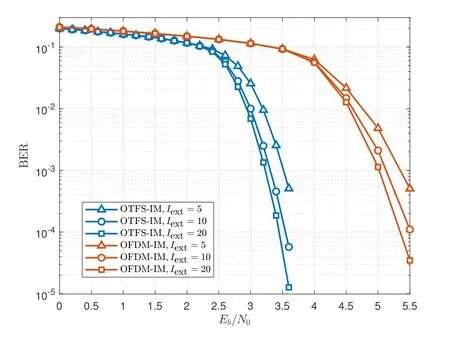
Figure 5. BER performance of the proposed Str-BP-EP based receiver in OTFS-IM and OFDM-IM systems with mode(4,2,2).

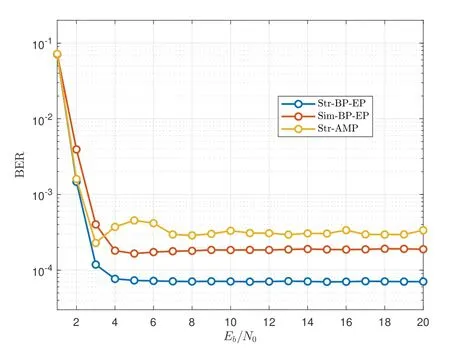
Figure 6. BER performance of Str-BP-EP,Sim-EP-BP and Str-AMP versus number of iterations in uncoded OTFS-IM system with mode(4,2,2).

In Figure 5,we further evaluate the BER performance of OTFS-IM and OFDM-IM systems with mode (4,2,2).It can be seen from Figure 5 that OTFS-IM outperforms OFDM-IM by almost 2dB at BER of 10-4.Since there are more active REs in a block,the inter-symbol interference of mode (4,2,2)is more severe than that of mode(4,1,4),which leads to a small BER performance degradation.

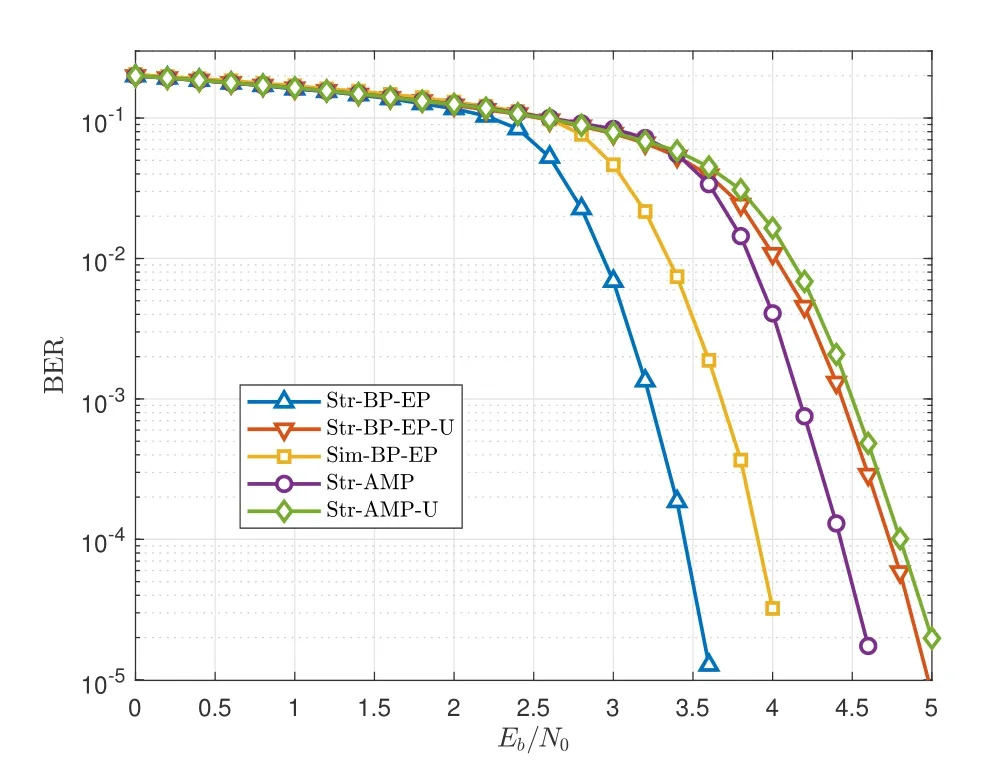
Figure 7. BER performance of Str-BP-EP and its counterparts in coded OTFS-IM system with mode(4,2,2).

In Figure 6,we compare the convergence of the proposed Str-BP-EP algorithm with its two variations,i.e.,simplified BP-EP (named as Sim-BP-EP)and Str-AMP.In order to see the comparison among these algorithms more intuitively,we consider uncoded OTFS-IM system with mode (4,2,2) so that the effect of turbo equalization is excluded.It is observed that the propose Str-BP-EP algorithm has better BER performance and faster convergence speed.Note that the convergence of AMP can be guaranteed only when Heffhas independent and identically distributed(i.i.d) entries due to the premise of the first-order approximation [34].Therefore,as the number of iterations increases,the BER performance of Str-AMP will fluctuate.This problem can be solved by introducing damping in AMP [35],while in BP-based algorithm,no damping is required.

In Figure 7,the BER performance of the proposed Str-BP-EP algorithm is studied for coded OTFSsystem.As comparison,uniform structured priorbased BP-EP (named as Str-BP-EP-U) and uniform structured prior-based AMP (named as Str-AMP-U)[17,18] are included.We can observe that Str-BP-EP outperforms Sim-BP-EP and Str-AMP about 0.5dB and 1dB at BER of 10-4,respectively,and outperforms Str-BP-EP-U and Str-AMP-U about 1.5dB.Since Str-BP-EP and Sim-BP-EP incorporate the LLRs from the decoder,they can exploit the channel coding gain by turbo equalization,and achieve better BER performance.Furthermore,by adopting the structured prior,Str-BP-EP achieves the best BER performance of all at a small sacrifice of computational complexity.Besides,despite the structured prior,Str-BP-EP-U outperforms Str-AMP-U.This is because Str-AMP-U suffers degradation due to the non-i.i.d channel,as stated above.

V.CONCLUSION

In this paper,we proposed a structured prior-based hybrid BP and EP algorithm for the iterative receiver design of LDPC-coded OTFS-IM system.Based on the factorization ofa posterioriprobability,we constructed the corresponding factor graph.We devised the structured prior that incorporates activation pattern constraint and channel coding by introducing the structured nodes on factor graph.To obtain lowcomplexity message updating rules of BP,we employed EP to approximate the discrete distribution introduced by structured prior.Furthermore,approximations were adopted to derive two low-complexity variations of Str-BP-EP,namely,simplified BP-EP and Str-AMP.Simulation results show that the proposed algorithm can significantly improve the BER performance of LDPC-coded OTFS-IM system.

APPENDIX

Substituting(46)into(24)we have

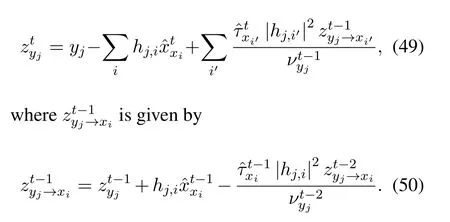
After some algebra,it reads

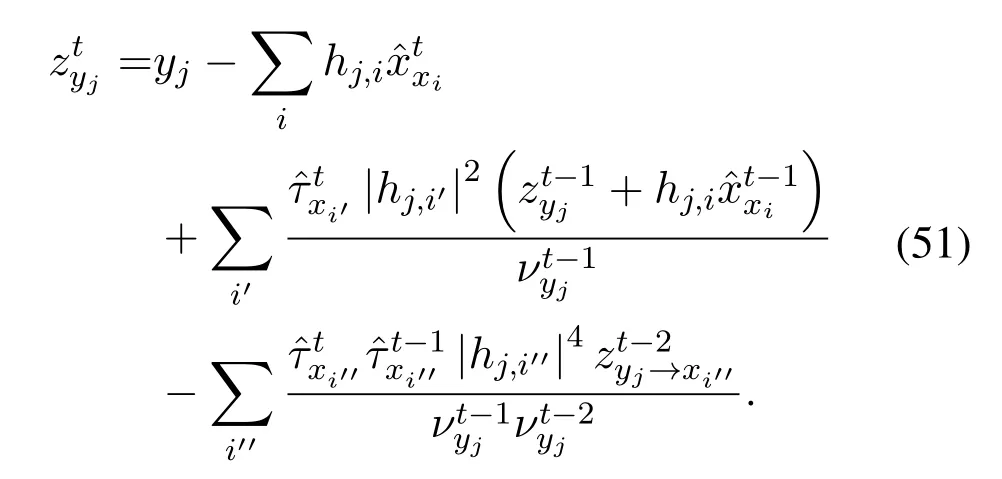
According to the assumption abouthj,i,the third term in the right side of (50) approaches to.By using first-order approximation,i.e.,neglecting terms with|hj,i|4,we obtain(47).

Substituting(46)and(50)into(28),we have

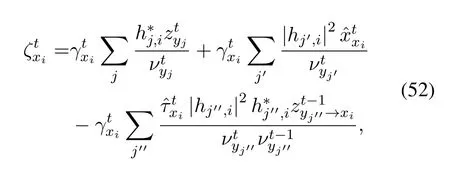
where the second term in the right side of(52)equals toaccording to (45).Similar to the derivation of,we could obtain(48)by using first-order approximation,i.e.,neglecting terms with

ACKNOWLEDGEMENT

This work was supported in part by the National Key Research and Development Program of China(No.2021YFB2900600);in part by the National Natural Science Foundation of China under Grant 61971041 and Grant 62001027.