BER Performance Analysis of OTFS Systems with Power Allocation

Zhenduo Wang,Zhipeng Liu,Zhiguo Sun,Xiaoyan Ning

College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China

Abstract: Orthogonal time frequency space(OTFS),as a novel 2-D modulation technique,has been proposed to achieve better BER performances over delay-Doppler channels.In this paper,we propose two different power allocation(PA)algorithms in OTFS systems with zero forcing(ZF)or minimum mean square error (MMSE) equalization,where general formulas with PA are derived in advance under the condition of minimum BER (MBER) criterion.On one hand,a suboptimal MBER power allocation method is put forward to achieve better BER performances,and then analytical BER expressions are derived with proposed PA strategy.Considering the case of MMSE equalization,a combined subsymbol allocation (SA) and PA strategy is raised,where some subsymbols may be abandoned due to worse channel conditions,and then it is proven effectively to improve BER performances through theoretical and simulation results.Furthermore,BER performances with proposed joint SA and PA strategy are also investigated in delay-Doppler channels,where an improved message passing (MP)receiver based on equivalent channel matrix with PA is given.

Keywords: OTFS;PA;ZF;MMSE;BER analysis

I.INTRODUCTION

In Sixth-generation (6G) wireless networks,mobile communication scenarios,such as unmanned aerial vehicles and high speed rails,have gradually becoming common,which means that high reliability should be guaranteed in double-selective fading channels with strong Doppler spread.Although orthogonal frequency division multiplexing(OFDM)has been employed in fourth-generation(4G)and the emerging fifth-generation (5G) cellular systems,evolving techniques are investigated to improve robustness against frequency shifts and also to solve critical challenges in high-mobility environments.Recently,a novel modulation technique,called as orthogonal time frequency space (OTFS),is proposed to achieve better adaptability for high speed scenarios in comparison with OFDM scheme,which modulates signals in delay-Doppler (DD) domain [1-5].It is illustrated that delay-Doppler domain can achieve stable sparse representations for time-varying channels,and thus a significant advantage of BER performances can be achieved in OTFS scheme.Additionally,it is demonstrated in [6] that OTFS and asymmetric OFDM (AOFDM)systems have equivalent transmitter structure,and thus appear same BER performances over static multipath channels.According to flexible energy distribution characteristics,flexible BER and peak-toaverage power ratio(PAPR)performances are also obtained in OTFS.

Most of existing research topics for OTFS modulation focus on the design of linear or iterative receivers as well as their corresponding applications[7-15].According to the block cycle structure characteristics of equivalent channel matrix in OTFS scheme,zero forcing (ZF) and minimum mean square error(MMSE) equalizers are derived in [7],which greatly reduces the complexity in comparison with original equalizers under the condition of same BER performances.A low-complexity message passing (MP)receiver is proposed in [10] through using the sparsity of channels,which can be employed to reduce the inter-Doppler interference generated by fractional Doppler.Therefore,utilizing the MP receiving algorithm,OTFS systems appear superior BER performances in comparison with OFDM systems over timevarying channels.Additionally,it is also demonstrated in [11,12] that the MP receiver have certain advantages in BER performances in comparison with linear receivers.Furthermore,a unitary approximate MP receiver is proposed in [13] with efficient implementation,where the estimation of noise variance is incorporated and a certain advantage is illustrated.In[14],a novel hybrid signal detection,composed of maximum a posteriori(MAP)detection,is put forward for OTFS modulation.According to partitioning rules,the MAP detection can be applied to the subset with larger channel gains.Moreover,non-orthogonal multiple access(NOMA)techniques have been investigated in OTFS waveform[16-18].In[16],multi-user interference is avoided through allocating non-overlapping parts to different user terminals,where resources are divided in delay-Doppler domain with higher spectrum efficiency.In addition,code-domain NOMA and tandem spreading multiple access have been used in OTFS[17,18].

Various resource allocation methods,such as power allocation (PA) and subcarrier allocation,have been widely investigated in OFDM systems [19-23].In[19],it assumes that the transmitter has a perfect estimation of channel state information (CSI),and then the time domain channel matrix can be transformed into a diagonal matrix in frequency domain by SVD decomposition,where different power allocation schemes are used to improve performances of OFDM systems,such as minimizing BER.To maximize sum rate with a minimum power constraint,a subcarrierseparation resource allocation method is proposed in[20] for multiuser OFDM systems with simultaneous wireless information and power transfer,which is formulated as a mixed integer programming problem.In [21],the problem of energy-efficient resource allocation of OFDM systems is addressed,where user scheduling and power allocation are optimized with a constraint on maximum transmitted power.A joint subcarrier allocation and power allocation algorithm is proposed in[22]to achieve a minimization of overall transmit power consumption for energy saving,where a constrained optimization problem is considered to derive the optimal allocation scheme.In [23],a generalized power allocation algorithm aiming at maximization of channel capacity for OFDM systems is proposed,where the optimization of sensing duration,user scheduling,and power allocation are investigated.A unified framework of power allocation in hybrid carrier scheme is proposed in [24],where closed BER expressions of related PA methods are derived.Due to the strong compatibility in multicarrier waveforms,power allocation strategies can be considered to further improve performances of OTFS scheme.In[25],the power allocation of pilot signals are claimed in OTFS systems,where impacts of power allocation on BER and PAPR performances are demonstrated.However,further power allocation methods,especially for optimizing BER performances,have not been widely investigated in OTFS waveform.

In this paper,we propose two different PA algorithms to improve BER performances of OTFS modulation over static multipath and delay-Doppler channels,where minimum BER (MBER) criterion is considered according to theoretical BER analyses of OTFS with ZF or MMSE equalization.On one hand,general BER expressions with power allocation are derived according to ZF receiving criteria,and then an approximate MBER power allocation method is given,where analytical BER expressions are also derived.On the other hand,a joint subsymbol allocation(SA)and PA algorithm is proposed for the case of MMSE equalization,which also originates from minimum BER criterion,and thus theoretical BER expressions are derived and further proven by simulation results.Additionally,we also investigate BER performances with proposed power allocation methods over delay-Doppler channels,and then better BER performances are still obtained according to an improved equivalent channel matrix with power allocation used in message passing receiver.

II.OTFS FRAMEWORK

2.1 System Model

In OTFS waveform,it is assumed that aNc ×1 vector xDDis expressed in DD domain at the transmitter,and then it can be further reshaped into aN ×Mmatrix XDDwithNc=MN,whereNandMdenote the number of subcarriers and subsymbols,respectively.The symbols in DD domain can be mapped to time-frequency (TF) domain through inverse symplectic finite Fourier transform(ISFFT),which can be expressed as

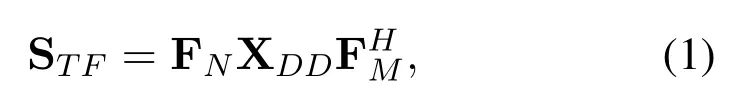
where FNanddenoteN-point Fourier transform matrix for each column of XDDandM-point inverse Fourier transform matrix for each row of XDD,respectively.After that,Heisenberg transform is used to transform TF domain signals into time domain [26],and there is

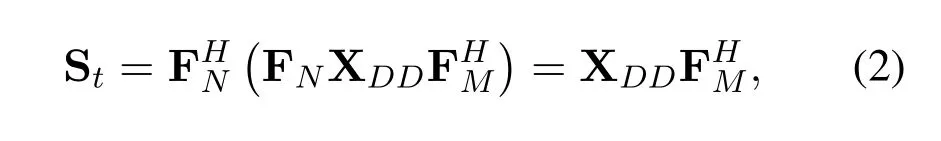
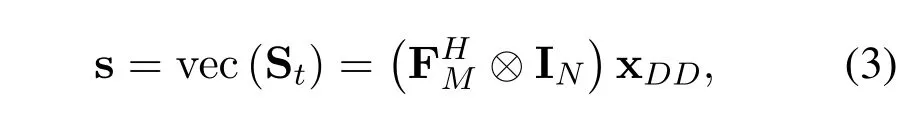
where⊗operation denotes Kronecker product and vec(·) operation denotes the column vectorization of anN ×Mmatrix into anNM ×1 column vector.

At the receiver,the time domain signal is expressed as

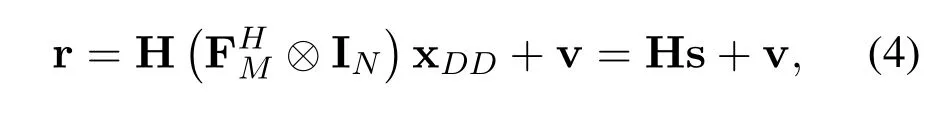
where H and v denote anNM ×NMtime domain channel matrix and additive white Gaussian noise(AWGN),respectively.

Correspondingly,by using Wigener transform and symmetric finite Fourier transform (SFFT) successively at the receiver,the DD domain signals can be obtained.Note that,different linear and iterative receivers can be used to demodulate transmitted information.

2.2 BER Analysis

In this subsection,theoretical BER expressions of OTFS systems over multipath channels are derived for subsequent analysis with power allocation.It has been proven that OTFS and A-OFDM scheme have the same structure over static multipath channels,and thus theoretical analyses of OTFS systems with ZF or MMSE equalization follow that in[27,28].However,we should note that traditional linear equalizations can not completely remove Doppler interference,and thus some equalization methods based on decision feedback and online learning are put forward in[29-31].

2.2.1 ZF Equalization

For static multipath channels,the channel matrix can be diagonalized by following calculation on basis of adding cyclic prefix,expressed as

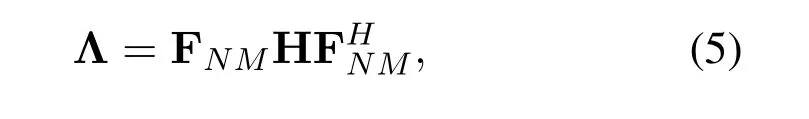
where Λ is a diagonal matrix,and its diagonal elements are eigenvalues of matrix H,written as[h1,h2,...,hNM].Thereby,Λ can be expressed as

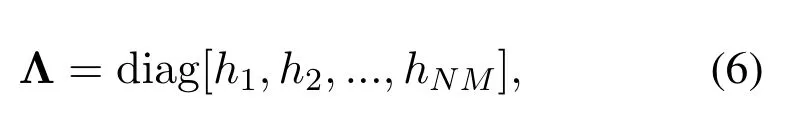
where diag[·]represents a diagonal matrix.

According to block diagonal structure given in [6],the whole transmitting process and receiving process in frequency domain can be given by

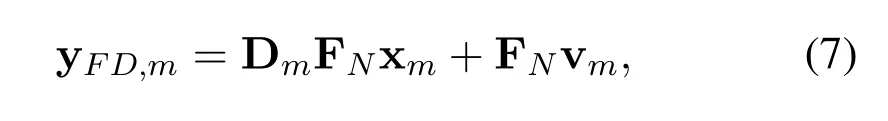
where Dmis a diagonal matrix,and there is Dm=diag[h(m-1)N+1,h(m-1)N+2,...,hmN] withm=1,2,...M.yFD,mand xm=(St)mdenotemth column of frequency domain received signal matrix andm-th column of time domain transmitted signal matrix,respectively.

Considering ZF equalization at the receiver with,the received signals in time domain can be expressed as

After that,Wigener transform and SFFT can be used to recover signals in delay-Doppler domain.According to[28],the SNR of received signals with ZF equalization can be expressed as

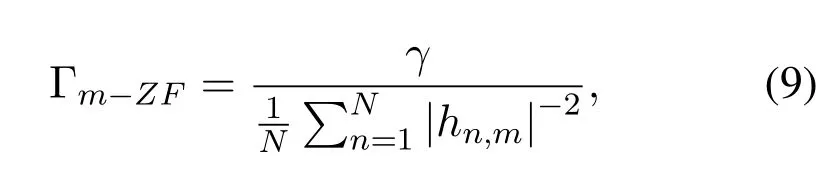
wherehn,m=h(m-1)N+ndefines then-th diagonal element in Dmwithn=1,2,...N.The SNR is expressed asγ=Es/N0,whereEsandN0denote the energy of transmitted symbol and the variance of noise,respectively.

Therefore,theoretical BER expression ofJ-QAM modulated OTFS scheme with ZF equalization is derived as

2.2.2 MMSE Equalization

For MMSE equalization,the MMSE equalizer is defined as

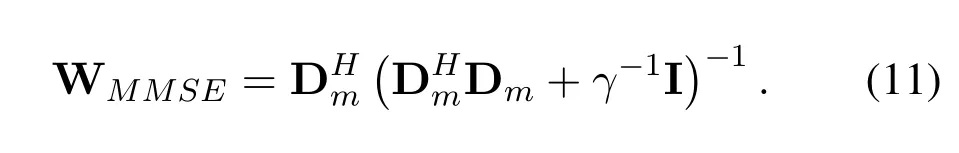
Similar as(8),the received time domain signal vector is given as

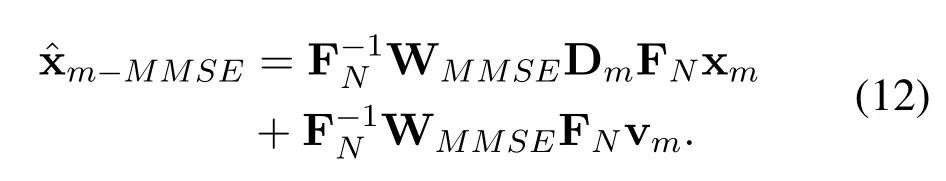
As a result,thei-th element ofm-MMSEis expressed as

Accordingly,the power ofi-th received symbol,desired signal and interference-plus-noise can be expressed as

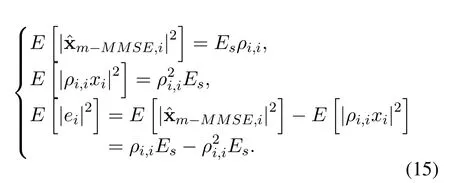
The signal to interference plus noise ratio (SINR) is calculated as

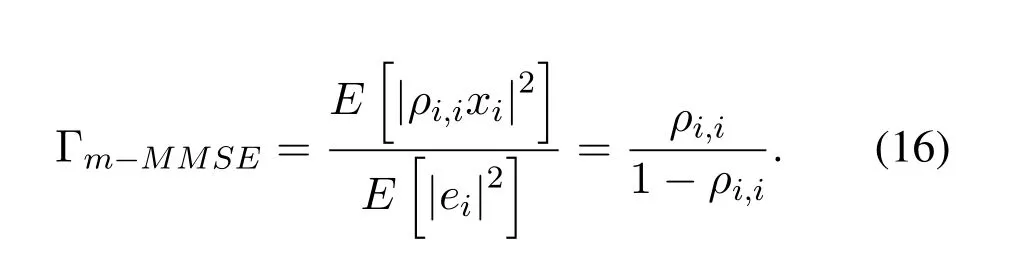
Replaceρi,iin(14),and the SINR is presented as

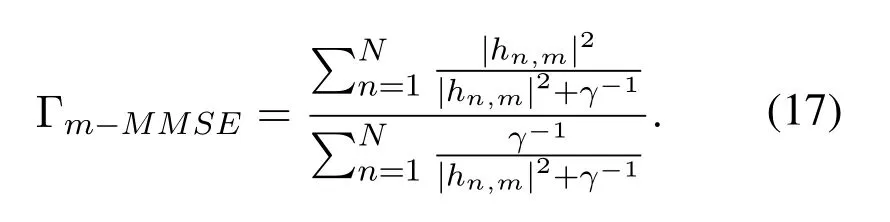
According to BER expression in[28],theoretical BER expression of OTFS scheme with MMSE equalization can be expressed as

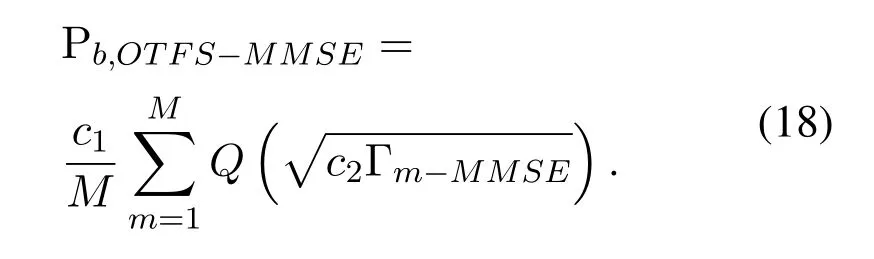
Substituting (17) into (18),and the final theoretical BER expression of OTFS scheme is given by

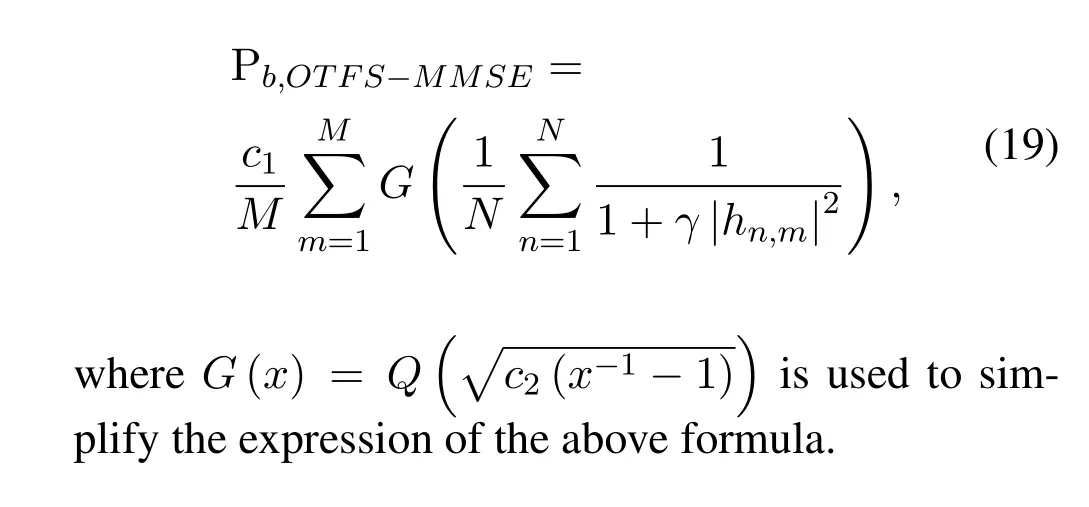
III.OTFS WITH POWER ALLOCATION

In this section,according to previous theoretical BER analyses,two different power allocation strategies are derived according to minimum BER criterion.As shown in Figure 1,the OTFS framework with power allocation is displayed,where ZF equalization,MMSE equalization and MP algorithm are considered at the receiver.

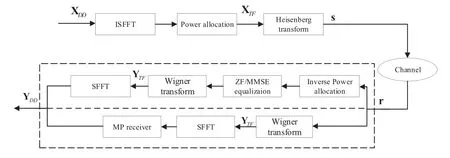
Figure 1. OTFS waveform framework with power allocation.

Figure 2. BER performances of OTFS systems with MBER power allocation over static multipath channels.

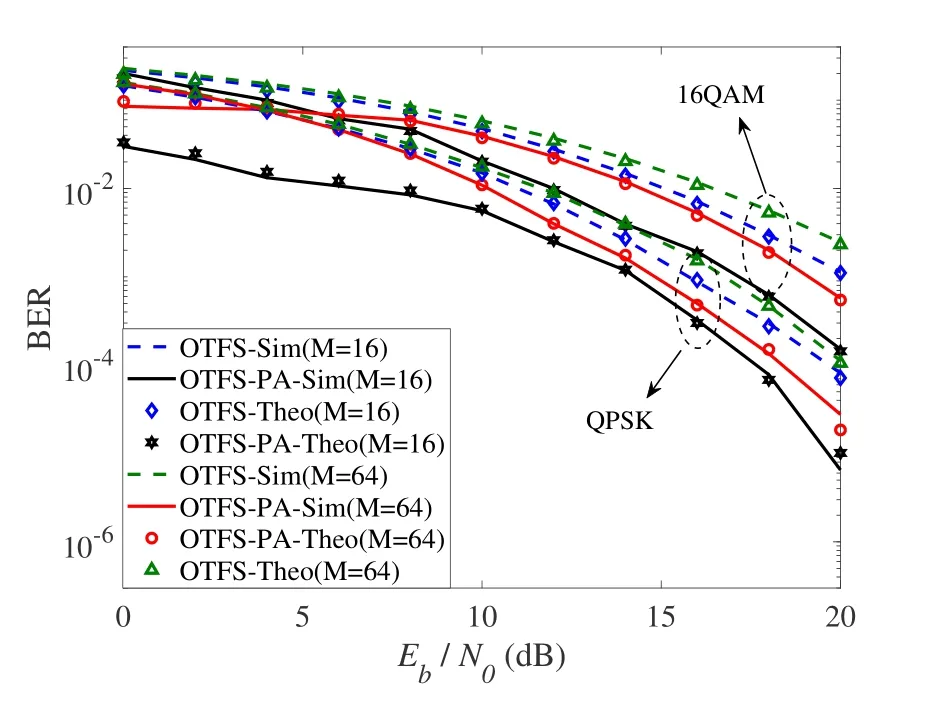
Figure 3.BER performances of OTFS systems with joint SA and PA method over static multipath channels.

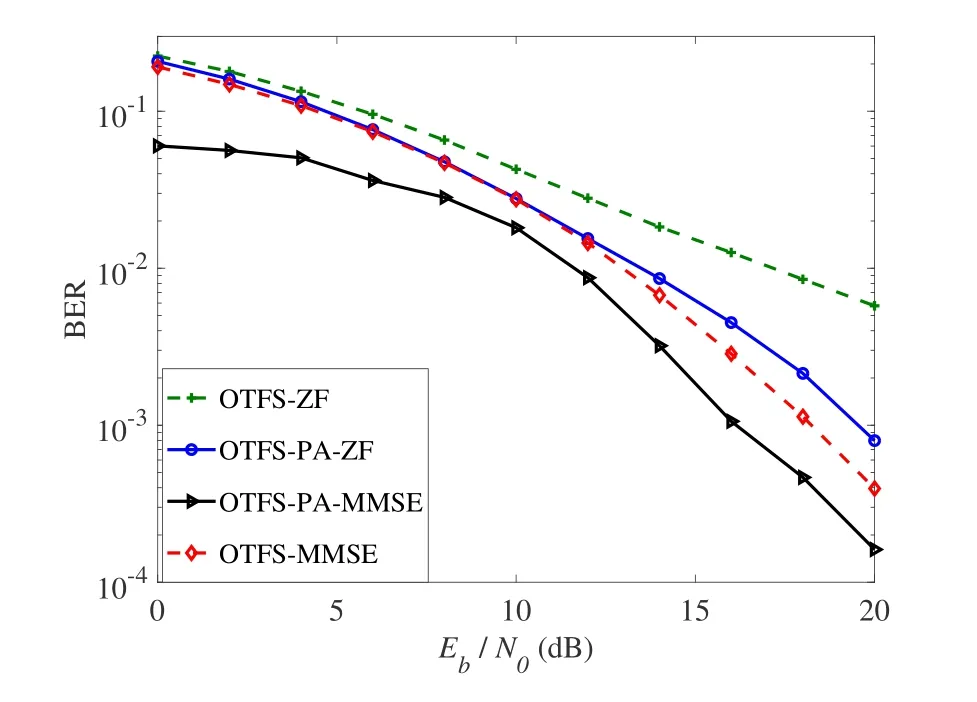
Figure 4. BER performances of OTFS systems with proposed power allocation under the case of ZF or MMSE equalization over delay-Doppler channels.

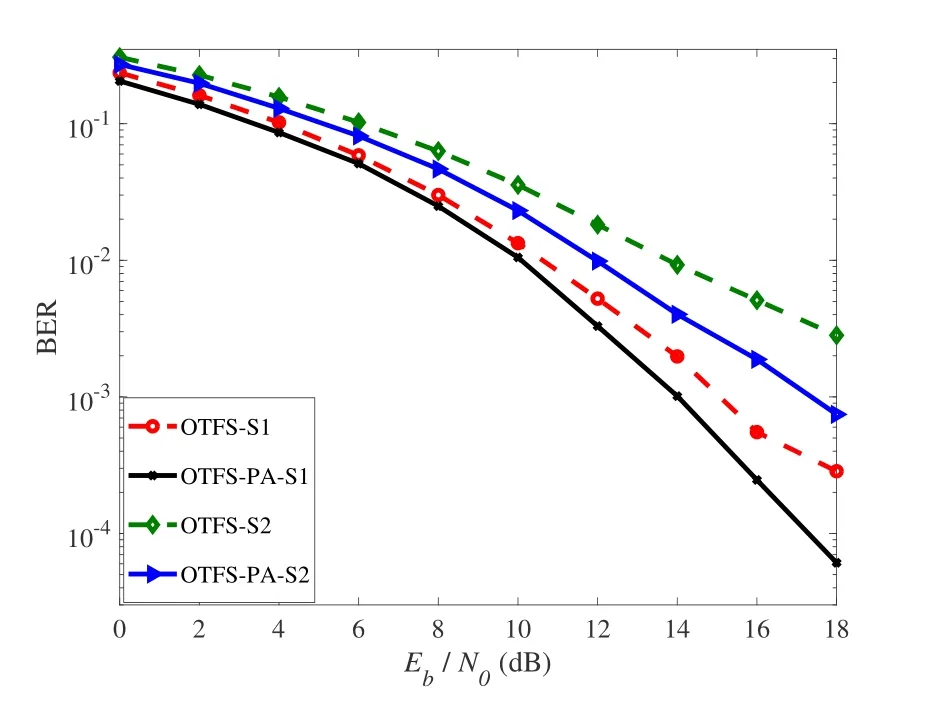
Figure 5. BER performances of OTFS systems with proposed joint SA and PA method under the case of MP receiver over delay-Doppler channels.

3.1 MBER PA in ZF Criterion

In OTFS scheme with power allocation,a diagonal matrix P can be used to describe the operation process,where diagonal elements are defined as[p1,p2,...,pNc].In addition,the power allocation matrix P=diag[p1,p2,...,pNc]satisfies

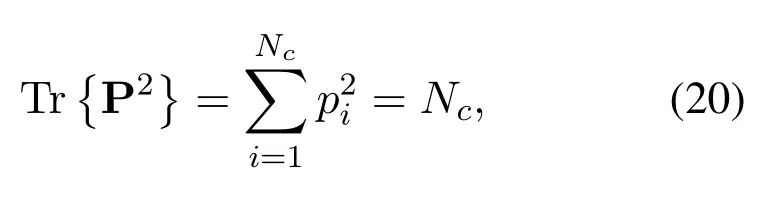
whereNc,i.e.the number of symbols in one OTFS block,is also the total power constraint.

Similar as that in(7),the whole transmitting process and receiving process in frequency domain with power allocation can be given as

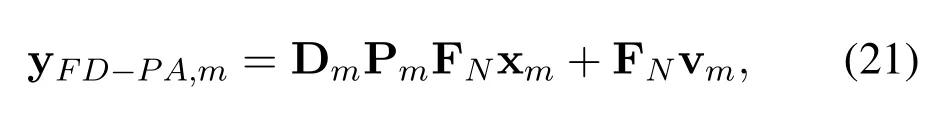
where Pmis a diagonal matrix and then-th diagonal element of Pm,i.e.pn,m,is given as [Pm]n=p[N(m-1)+n]with p=[p1,p2,...,pNc].

According to ZF receiving criteria both for channel equalization and inverse PA process,i.e.of the inverse PA module,the obtained signals are shown as

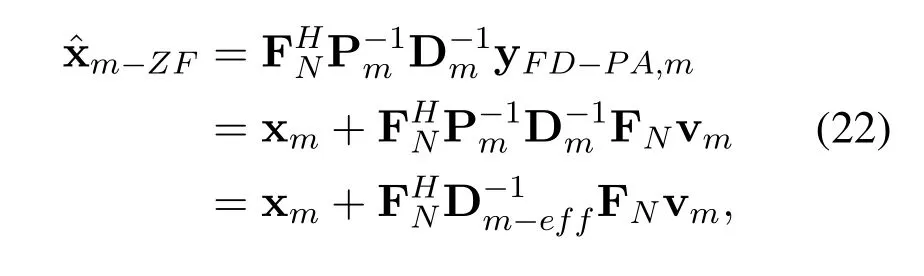
where Dm-eff=DmPmdenotes the equivalent channels matrix with power allocation.

Therefore,on basis of ZF receiving criteria,analytical BER expressions of OTFS scheme with power allocation are derived as

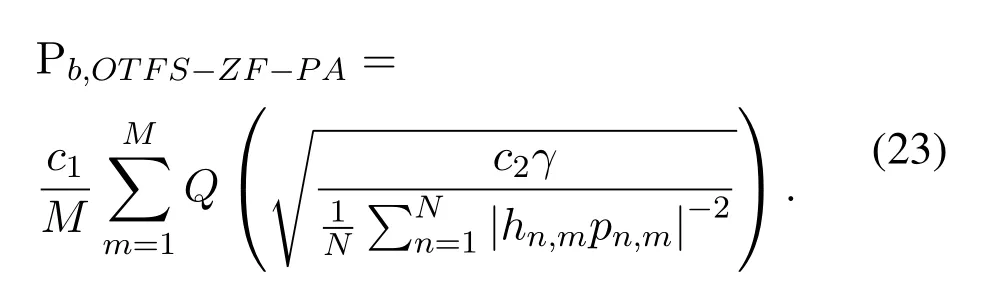
where the SNR of each subsymbol is calculated as

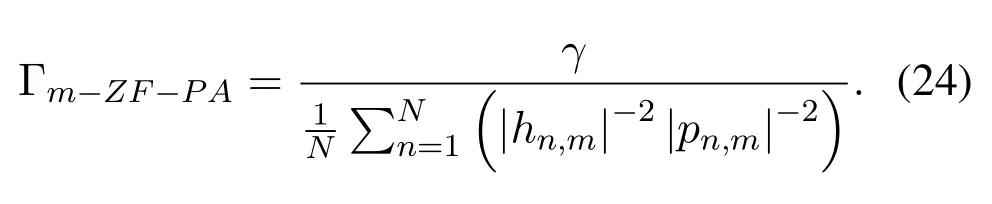
Note that,a general theoretical BER formula with power allocation has been derived.If a power allocation strategy has been determined,its theoretical BER can be obtained by(23).Therefore,according to MBER criterion,the optimal power allocation mode can be solved through

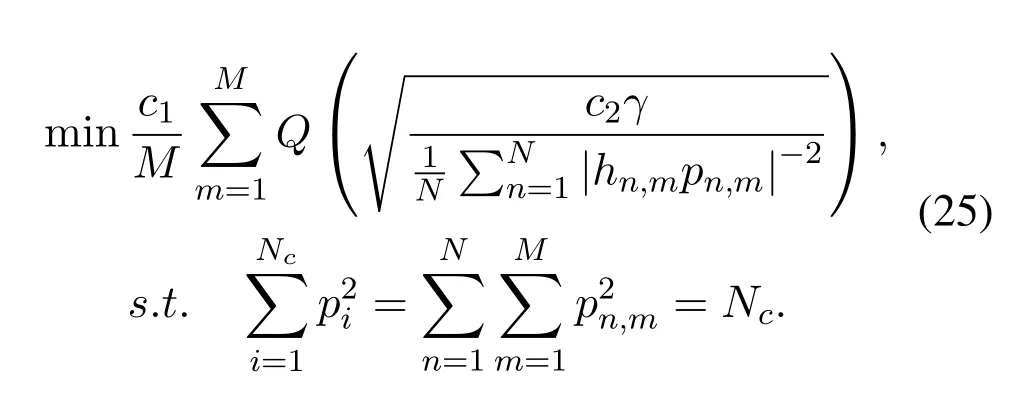
It seems that the above optimization equation is difficult to solve,and thus a simplified form is given.Compared to OTFS without PA,MandNshould be unchanged.Besides,it is assumed that the value ofγis constant during the process of power allocation and the total transmit power is equally allocated toMsubsymbols.Consideringm-th subsymbol,according to the monotonicity ofQfunction,(25)is simplified to

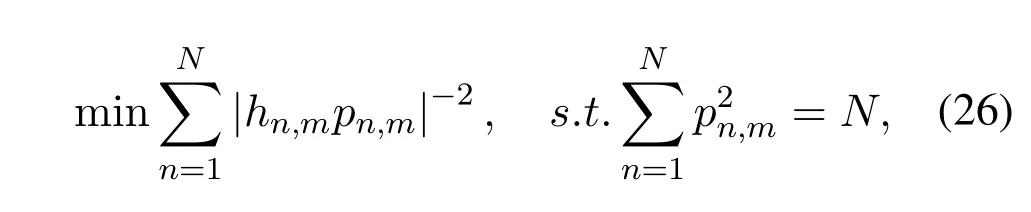
which can be regarded as a suboptimal MBER criterion.Using the Lagrange multiplier method to (26),we get

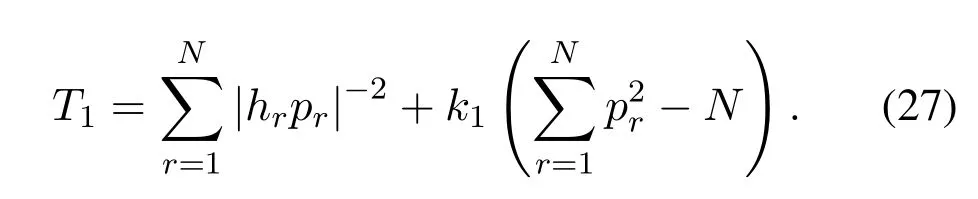
For the convenience of representation,the subscript is uniformly expressed asr.Calculating the derivative of (27),there is

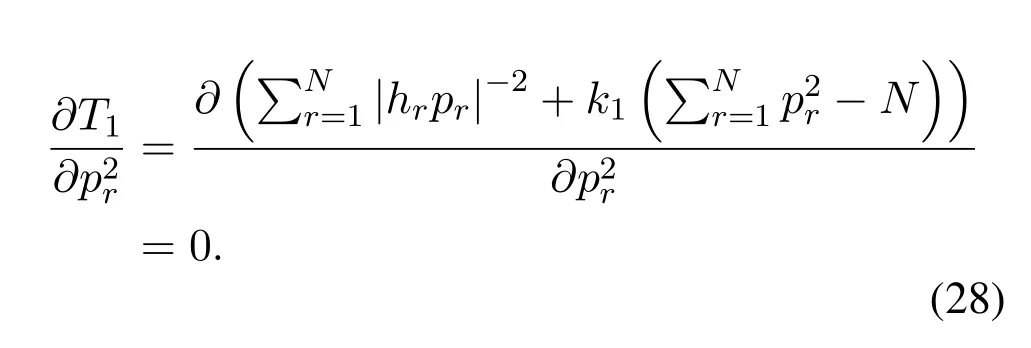
After setting the derivative as 0,we get.Hence,the power constraint in (26) can be written as

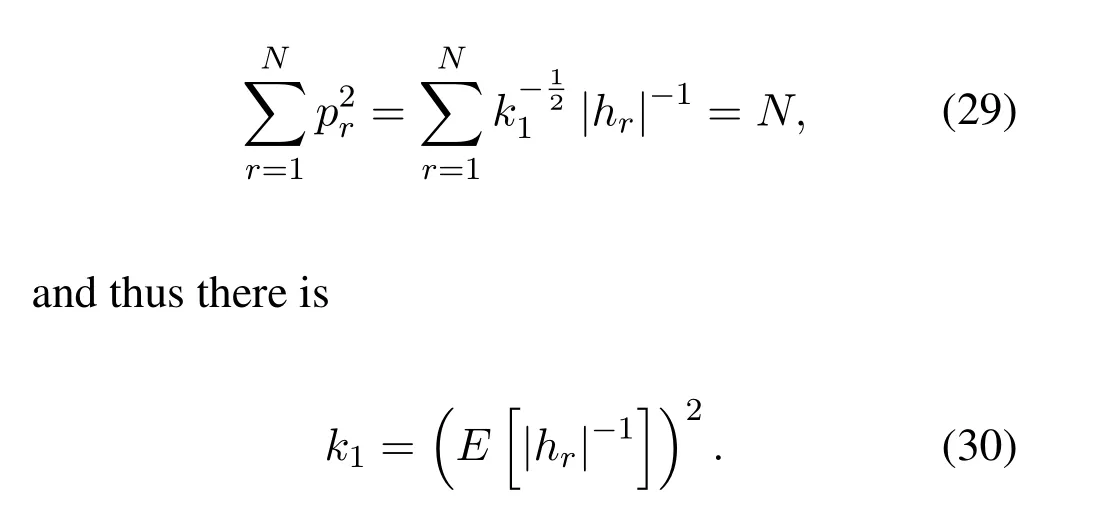
Finally,substitute(30)into formulaand the approximate MBER power allocation mode of OTFS systems with ZF equalization is calculated as

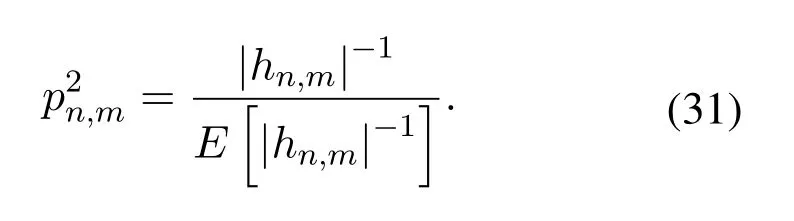
Considering the equivalence of all subsymbols,p2n,mis applicable to all subsymbols.Therefore,substitute(31)into(23),and the theoretical BER expression of OTFS scheme with MBER power allocation is derived as

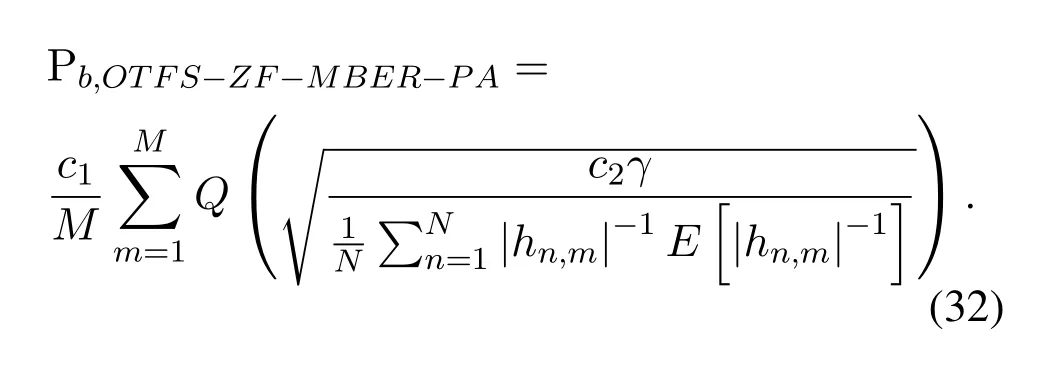
3.2 Joint SA and PA in MMSE Criterion

For MMSE receiver of OTFS scheme,we can follow the analysis process of ZF equalization.The inverse PA module refers to the MMSE receiving criterion of considered power allocation at the transmitter.Therefore,under the condition of MMSE criterion,we get

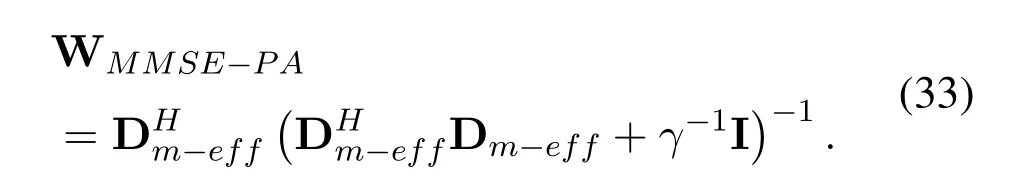
The estimated signal after MMSE equalization is expressed as

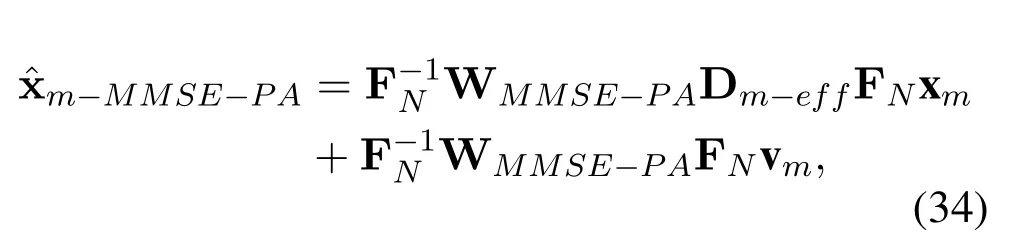
where thei-th element can be expressed as

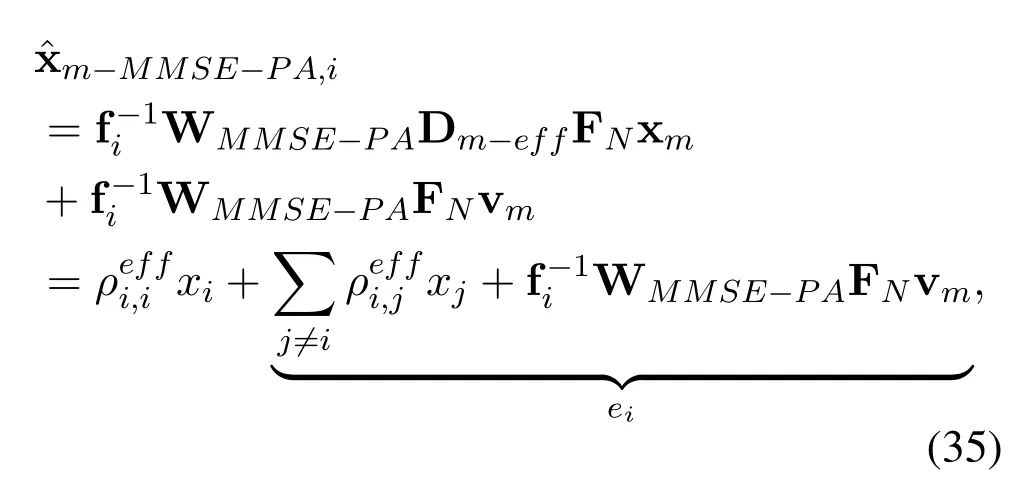
where two parameters are given as

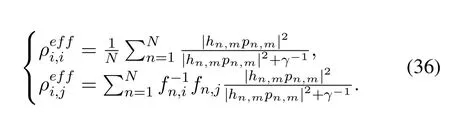
Similarly,the SINR with power allocation is

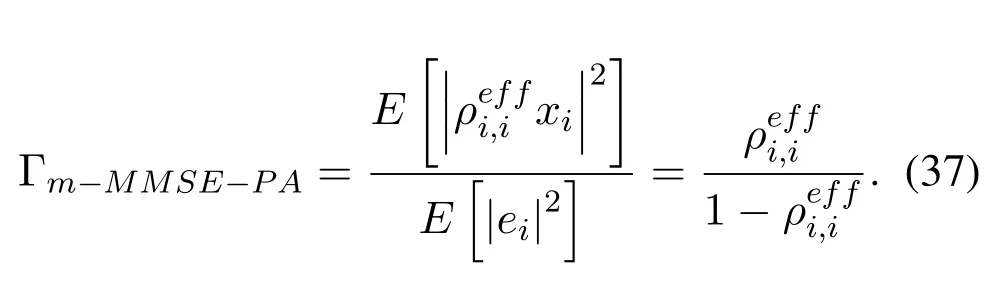
Furthermore,substituting(36)into(37),there is

Therefore,according to MMSE receiving criterion,the general theoretical BER expression of OTFS scheme with power allocation is derived as

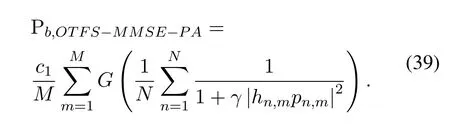
Therefore,in order to solve the optimal power allocation for the case of MBER criterion,the optimization equation is given as

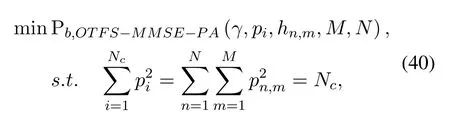
where Pb,OTFS-MMSE-PAis function of variablesγ,pi,hn,m,MandN.Similar to the analysis in ZF receiving criteria,the (40) with fixedγ,MandNcan be simplified to

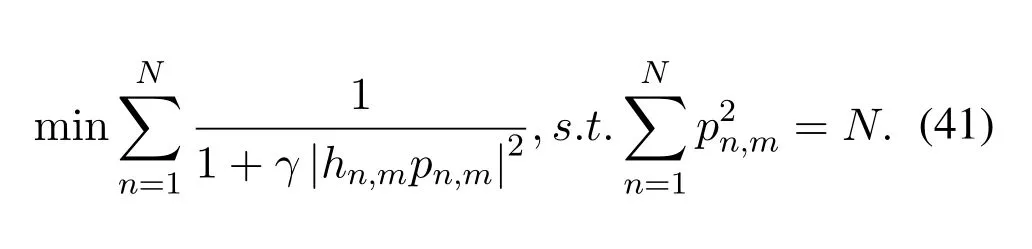
As a result,the power allocation expression under the condition of MBER criterion with MMSE equalizer can be derived through using the Lagrange multiplier method of(41),which is expressed as

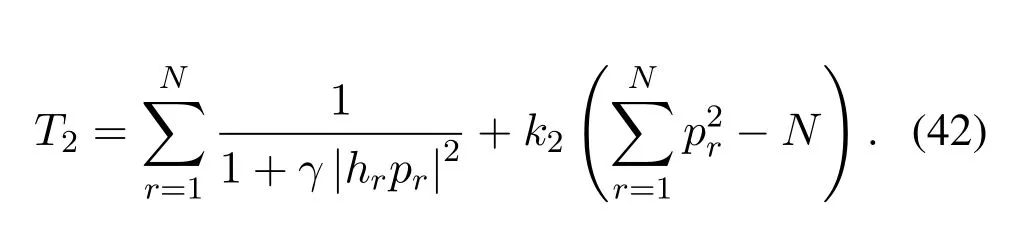
where the subscript is also replaced withrfor the convenience of writting.Calculate the derivative of(42),and there is

Substitute(44)into(41),and there is

Finally,the power allocation factor is obtained as

Similarly,power allocation factors ofm-th subsymbol are applicable to all subsymbols.Besides,we note that the calculatedmay be less than 0,which is not allowed whether in practice or in theory.Thereby,a joint SA and PA method is raised in Algorithm 1,where some subsymbols are not used to transmit data at,and thus the proposed joint algorithm contributes to solving this problem.The specific descriptions of this algorithm are shown.

Additionally,considering discarded subsymbols and also substituting (46) into (39),theoretical BER expression of OTFS scheme with joint SA and PA is derived in(47),where U denotes the set of discarded subsymbols.

3.3 MP Receiver with PA

As an iterative detection algorithm,MP receiver as well as its improved versions are widely used to improve BER performances of OTFS over delay-Doppler channels,which can be regarded as a combination process of channel compensation and signal demodulation.Therefore,necessary theoretical analyses for MP receiver are also given to demonstrate the comprehensive performances of proposed PA strategies.

In (22),the channel matrix Dmwith power allocation is equivalent to Dm-eff.Thereby,we consider that the relationship between signals at the transceiver in DD domain can be established through an equivalent matrix with channel and waveform information.Note that,the power allocation matrix is calculated according to frequency domain channel information.

At the transmitter,the symbols in DD domain are transformed into time domain through ISFFT and Heisenberg transform.Correspondingly,at the receiver,time domain symbols can be transformed into DD domain through Wigener transform and symmetric finite Fourier transform(SFFT).According to[26]and (4),this process is given in (48).The power allocation matrix is then taken into account,and thus we can get(49),where equivalent channel matrix with power allocation can be written as HDD-PA.Particularly,formula (49)is simplified to(48)at P=I.

Therefore,considering the decision process in DD domain in [10],the equivalent channel matrix of improved MP receiver based on power allocation is HDD-PA.The decision process can be expressed by maximum a posteriori probability detection rule,and estimated signal is given as

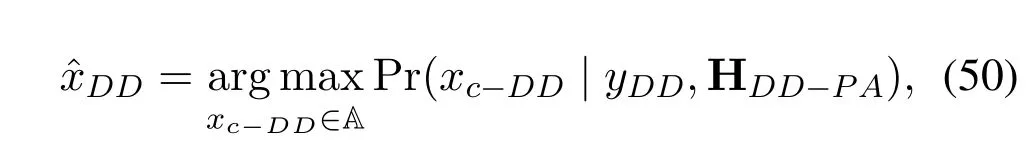
wherexc-DDandyDDdenote possible constellation points and received symbols in DD domain,respectively.A denotes modulation alphabet with A=[a0,a1,...,aJ]forJ-QAM modulation,andaidenotes signal constellation.The interference-plus-noise termζiofi-th received symbol through HDD-PAcan be expressed as

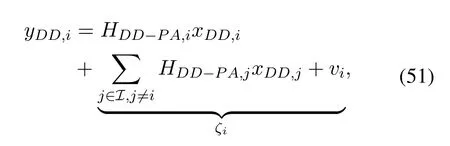
whereIdenotes the set of transmitted symbols,videnotes corresponding additive white Gaussian noise.In addition,ζiis approximated as Gaussian random variable [10].Therefore,in MP algorithm,the mean and variance ofζican be calculated and then transmitted between variable nodes and observation nodes.According to the iterative detection of improved MP receiver with power allocation,the output symbols in DD domain are directly obtained.

IV.SIMULATION RESULTS

In this section,simulation results are given to illustrate the performance superiority of proposed power allocation algorithms.In order to achieve comprehensive analyses of OTFS modulation,static multipath and delay-Doppler channels are both considered.Correspondingly,different receivers,including ZF equalization,MMSE equalization and MP algorithm,are employed to fight channel interference.In addition,in some scenarios,QPSK and 16QAM are both considered to reveal the correctness and generality of given theoretical analyses.

In Figure 2,BER performances with suboptimal MBER power allocation criterion in (31) under the condition of ZF receiving criteria are given.Specifically,a 5-path static multipath channel is considered,and each path follows an independent Rayleigh distribution.The relative delay and average power of each path are set as[0,100,200,300,500]ns with sample period 10ns and[0,-2,-4,-8,-16]dB,respectively.In addition,it is assumed thatN=16,M=16 andN=4,M=64 in OTFS scheme.As shown in Figure 2,it is proven that BER performances can be significantly improved by proposed power allocation strategy,where theoretical BER expressions in (32)are also verified by simulation results.

In Figure 3,BER performances with the proposed joint PA and SA algorithm under the condition of MMSE equalization are shown.In order to illustrate applicability of proposed algorithm,the static multipath channels with different parameters are considered,where the relative delay and average power of each path are set as[0 100 250 300 350]ns with sample period 10ns and [0,-3,-6,-9,-12]dB,respectively.OTFS parameters are also assumed asN=16,M=16 andN=4,M=64 for QPSK and 16QAM modulations.It is clearly demonstrated in Figure 3 that BER performances of OTFS scheme are obviously improved by joint SA and PA strategy.Additionally,analytical BER expressions in(47)are verified by the coincide results between theoretical and simulated curves.

Furthermore,delay-Doppler channels,i.e.complex time-varying channels,are also considered in Figure 4 to display advantages of proposed power allocation algorithms.Channel parameters of ZF receiver are same as those in Figure 2,and there isN=16,M=16 of OTFS system.Similarly,channel and waveform parameters in Figure 3 are also used for MMSE receiver withN=M=16.Note that,the Doppler frequency shifts are [0,0,0,1,2]×390 KHz and[0,0,1,2,3]×390 KHz for ZF and MMSE equalization respectively,where carrier frequency is set as 4 GHz.As shown in Figure 4,although ZF or MMSE equalization can not significantly suppress Doppler shifts,which leads to a narrowed gap of BER results,the superiority of BER performances are still obtained with power allocation.

In order to improve BER performances of OTFS systems and also to illustrate the validity of proposed joint SA and PA strategy,BER performances of the MP receiver based on equivalent channel matrix with power allocation are also given.As shown in Figure 5,two different channel scenarios are considered.In scenario 1(S1),the relative delay,average power of each path and normalized doppler frequency shifts are set as[0,100,200,300,500]ns with sample period 10ns,[0,-10,-10,-15,-15]dB and[0,0,1,2,1]×390 KHz with carrier frequency 4 GHz,respectively.In scenario 2(S2),the relative delay,average power of each path and doppler frequency shift are set as [0,100,200,300,500]ns with sample period 10ns,[0,-6,-12,-18,-24]dB and[0,0,2,3,1]×390 KHz with carrier frequency 4 GHz,respectively.In addition,we assume thatN=4 andM=32 in OTFS scheme with 4QAM modulation.Accordingly,we conclude that proposed joint SA and PA strategy is also effective to improve BER performances of OTFS systems over delay-Doppler channels with MP receiver.

V.CONCLUSION

In this paper,we theoretically derive generalized BER expressions of OTFS systems with power allocation under the condition of ZF or MMSE receiving criteria over static multipath channels.Furthermore,two different power allocation methods are put forward on the basis of minimizing BER.Specifically,analytical BER expressions with approximate MBER PA under the condition of ZF criterion are derived.Additionally,a joint SA and PA strategy for MMSE criterion is proposed with possible discarded subsymbols,and then theoretical BER expressions are also derived.Moreover,theoretical BER expressions of proposed PA algorithms are both verified by simulation results.Finally,considering the MP algorithm based on equivalent channel matrix with PA,BER performances can also be improved over delay-Doppler channels,which illustrates the generality and validity of proposed PA methods.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China under Grant 62001138,Heilongjiang Provincial Natural Science Foundation of China under Grant LH2021F009,China Postdoctoral Science Foundation under Grant 2020M670885,Hei Long Jiang Postdoctoral Foundation under Grant LBH-Z20049.