Secrecy Rate Maximization for 6G Cognitive Satellite-UAV Networks

Chengleyang Lei ,Wei Feng,* ,Yunfei Chen ,Ning Ge

1 Department of Electronic Engineering,Tsinghua University,Beijing 100084,China

2 Beijing National Research Center for Information Science and Technology,Tsinghua University,Beijing 100084,China

3 School of Engineering,University of Warwick,Coventry CV4 7AL,United Kingdom

Abstract: To cover remote areas where terrestrial cellular networks may not be available,non-terrestrial infrastructures such as satellites and unmanned aerial vehicles (UAVs) can be utilized in the upcoming sixth-generation (6G) era.Considering the spectrum scarcity problem,satellites and UAVs need to share the spectrum to save costs,leading to a cognitive satellite-UAV network.Due to the openness of both satellite links and UAV links,communication security has become a major concern in cognitive satellite-UAV networks.In this paper,we safeguard a cognitive satellite-UAV network from a physical layer security (PLS) perspective.Using only the slowlyvarying large-scale channel state information (CSI),we jointly allocate the transmission power and subchannels to maximize the secrecy sum rate of UAV users.The optimization problem is a mixed integer nonlinear programming (MINLP) problem with coupling constraints.We propose a heuristic algorithm which relaxes the coupling constraints by the penalty method and obtains a sub-optimal low-complexity solution by utilizing random matrix theory,the max-min optimization tool,and the bipartite graph matching algorithm.The simulation results corroborate the superiority of our proposed scheme.

Keywords: channel allocation;cognitive satellite-UAV network;physical layer security;power allocation

I.INTRODUCTION

Recently,the demand for communication services in remote areas has increased drastically [1,2].The future sixth generation (6G) wireless communication network is expected to cover remote areas efficiently [2,3].However,it is difficult and costly to deploy traditional terrestrial cellular networks in some remote areas,such as the ocean [4],due to the geographical environments therein.Consequently,nonterrestrial infrastructures should be considered.

Satellites,which can provide wide connectivity coverage,may be an alternative in remote areas [5-8].However,current satellite systems may not be able to provide high-quality communication services due to their limited data rate and inherently large latency[9,10].On the other hand,unmanned aerial vehicles(UAVs)have received growing attention in many tasks,such as spectrum monitoring[11],sea area coverage[10]and vehicular communications[12],due to their unique advantages such as high mobility and ondemand deployment,compared with traditional terrestrial and satellite communications [13].However,UAV communications may often be limited by the coverage and on-board energy of UAVs.To overcome their respective limitations,it is beneficial to integrate UAVs with satellites for higher quality of service(QoS)[14,15].

There are still some challenges for a hybrid satellite-UAV network to efficiently cover remote areas.For example,the spectrum scarcity problem may become serious because local spectrum reuse as cellular architecture is not applicable[3].Satellites and UAVs can share the spectrum to save costs to give a cognitive satellite-UAV network.In a cognitive satellite-UAV network,the interference to users must be considered.The security problem is a serious concern in a hybrid satellite-UAV system due to the open propagation environments.Specifically,fewer scatterers in UAV links and longer transmission distance of satellite links [3] make eavesdropping easier.However,traditional cryptographic methods with high computational complexity may not be suitable for UAV communications,due to the limited power of UAVs [16].Recently,physical layer security(PLS)has been considered in satellite-UAV networks,as it can safeguard satellite links and UAV links against eavesdroppers without the need for cryptographic methods[17].PLS exploits the inherent randomness of wireless channels to secure communications [16],which can make full use of the high mobility of UAVs.Motivated by these issues,in this paper,we study the PLS in cognitive satellite-UAV networks.

1.1 Related Works

There have been many studies on the cooperation between UAVs and satellites in wireless communications [14,18,15,9].In [14],the authors showed that high-altitude platforms (HAPs) could overcome the shortcomings of satellites,and they presented two integrated HAP-satellite architectures.Reference[15]utilized UAVs to enhance the coverage of a hybrid satellite-terrestrial maritime communication network.The UAV trajectory and in-flight transmission power were jointly optimized.The authors in [18] investigated the satellite-UAV spectrum allocation problem and presented the development of an on-board Kaband tracking antenna to meet the need for UAV control and non-payload communications (CNPC) links between UAVs and satellites.In [9],a cognitive satellite-UAV network to support massive access for Internet of Things (IoT) devices outside terrestrial cellular networks was investigated.The authors improved the network efficiency by jointly optimizing the channel allocation,transmission power and hovering times,with only slowly varying large-scale channel state information(CSI).However,the above works have not considered the security problem in satellite-UAV systems.

Using PLS techniques to safeguard UAV networks has recently been considered in many works[13,19-24].In [13],the transmission power and the trajectory of a UAV were jointly optimized to secure a UAVenabled wireless communication system where a UAV communicates with a node on the ground in the presence of an eavesdropper.Both UAV-to-ground(U2G)and ground-to-UAV(G2U)scenarios were considered.Cuiet al.further investigated the robust design of trajectories and transmission power of UAVs,considering the imperfect location information of multiple eavesdroppers[19].However,this paper only considers a simple system model with only one UAV and one user.Considering multiple users,Zhouet al.jointly optimized the transmission power and trajectories of two cooperative UAVs,one acts at a transmitter,and the other serves as a jammer[20].The above works assume that the channels between the UAVs and ground nodes follow the free-space loss model,which is too idealistic.Wanget al.considered a realistic channel model and utilized a UAV as a relay to safeguard a source-destination pair on the ground [21].In [22],multiple UAVs act as an aerial base station via coordinated multiple points (CoMP),and the transmission power of the UAV swarm was optimized to maximize the secrecy sum rate.These works did not take satellites into consideration.However,in satellite-UAV networks,the interference to satellite users is non-negligible Some works considered PLS in hybrid satellite-UAV networks[23,24].Reference[23]safeguarded a land mobile satellite system with a friendly UAV jammer.In [24],Sharmaet al.adopted UAVs as relays in a hybrid satellite-terrestrial network in the presence of an aerial eavesdropper.The secrecy performance of different UAV relay selection strategies was evaluated.However,in both works,UAVs only act as helpers in the networks,such as relays and jammers.

Although many works have been done on the PLS problem of UAV networks,there remain open challenges for safeguarding cognitive satellite-UAV networks.From the perspective of practical applications,more realistic channel models should be used instead of the ideal free-space path loss mode as in[13,19-21],so as to characterize the usually complicated propagation environments.Furthermore,the UAVs in a cognitive satellite-UAV network usually interact with the satellites,which adds interaction to the system.Thus,we should consider a more systematic model including both satellites and UAVs,rather than UAVs only [13,19-22].Due to the vastness of remote and maritime areas [2,3],multiple UAVs should be considered for cooperative coverage,and the performance of both satellite users and UAV users should be optimized,rather than simply using UAV as a helper[23,24].Furthermore,the resources for multiple users,such as power and subchannels,should be jointly allocated for better secrecy performance,rather than the single-user case[21,23].

1.2 Main Contributions and Organization

Motivated by these challenges,in this paper,we consider a typical cognitive satellite-UAV network consisting of a satellite and a UAV swarm in the presence of multiple eavesdroppers.PLS techniques are utilized to safeguard the network.Specifically,we maximize the secrecy sum rate of all UAV users by jointly optimizing the power allocation and channel allocation of the network,while keeping the leakage interference to satellite users below an affordable threshold.Besides,the maximum transmission power constraint for each UAV is also considered.The formulated problem is a mixed integer nonlinear programming(MINLP)problem with a non-convex objective function.To solve this problem,we propose a sub-optimal iterative algorithm,which relaxes the coupling constraints with the penalty method and obtains the sub-optimal channel and power allocation strategy using the bipartite graph matching algorithm and the max-min optimization tool.The simulation results demonstrate the superiority of the proposed scheme.The main contributions are summarized as follows.

• This paper investigates the security problem in a typical cognitive satellite-UAV network.The spectrum is divided into multiple subchannels to serve multiple users.We jointly allocate the transmission power and subchannels of UAVs to maximize the secrecy sum rate of the UAV users.A realistic channel model that considers both the lineof-sight(LOS)and non-line-of-sight(nLOS)elements is used in this paper.In addition,only the large-scale CSI is used in the optimization process to save costs.Compared with existing works,this paper is the first to safeguard satellite-UAV networks via joint sub-channel and power allocation.

• We formulate the optimization problem as an MINLP problem.To relax the coupling constraints,we use the penalty method and add a penalty term to the objective function.Next,an iterative method is proposed to get a sub-optimal solution to this problem.During each iteration,the problem is decomposed into several subproblems where the power allocation in a single channel is obtained with the max-min optimization tool.Based on the solution to the subproblems,the channel allocation problem is solved with the bipartite graph matching algorithm.

• We evaluate the performance of our proposed method with simulation.The numerical results show that the proposed method can achieve higher secrecy performance.

The remainder of this paper is organized as follows.Section II introduces the system model.In Section III,we formulate the secrecy rate maximization problem,and solve it in an iterative way by using random matrix theory and the penalty method.The proposed joint power and channel allocation algorithm is evaluated in Section IV by simulations.Finally,Section V summarizes this paper.

II.SYSTEM MODEL

As shown in Figure 1,we consider a cognitive satellite-UAV network,where a satellite and a swarm ofNUAVs serveKsatellite users andKUAV users on the ground respectively.The satellite and UAVs share the spectrum to save costs.The spectrum is divided intoKchannels,each supporting one satellite user and one UAV user simultaneously.Keavesdroppers are distributed around legitimate users,and each eavesdropper eavesdrops on one frequency channel to obtain the confidential messages from the UAV swarm.Due to the limited on-board energy of UAVs,we assume that only a single antenna is equipped on each UAV.Multiple UAVs operate in a coordinated manner,forming a virtual super aerial base station withNantenna elements.Both UAV users and eavesdroppers are equipped withNantenna elements for better communication and wiretap performance,respectively.

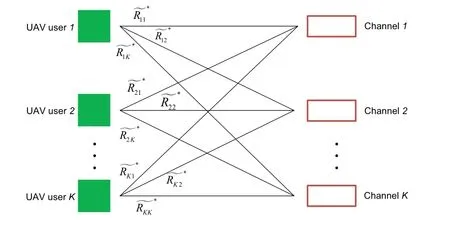
Figure 2. A bipartite graph model of(36).

The UAV swarm and ground nodes (UAV users,satellite users or eavesdroppers) form a distributed MIMO system.The received signal at thek-th ground nodes can be expressed as

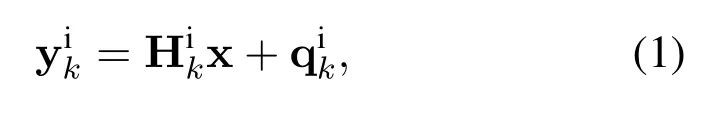
where i∈ {U,S,E}represents the type of ground nodes and U,S and E denote UAV users,satellite users and eavesdroppers respectively,k ∈ {1,2,···,K}represents the index of ground nodes,∈CN×Ndenotes the MIMO channel matrix between the UAV swarm and ground nodes,x∈CNdenotes the transmitted signal of the UAV swarm,anddenotes the additive white Gaussian noise with mean zero and covariance Σ.

In this paper,we consider a realistic channel model with both LOS and nLOS elements[25].The channel matrix can be expressed as

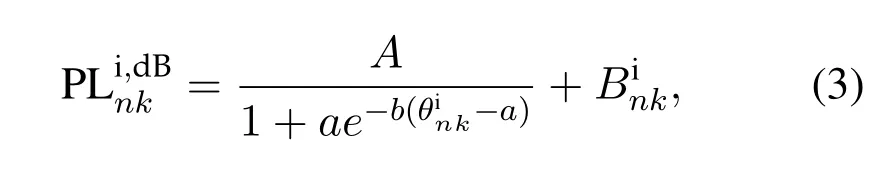
For the primary satellite subsystem,sophisticated user scheduling can be performed to serve each user in the most appropriate channel.Without any loss of generality,we assume that satellite userloccupies channell,and eavesdropperlwiretaps on channell.Therefore,we use the channel indexlto index satellite users and eavesdroppers instead ofkhereafter.Under this setup,we optimize the scheduling strategy of UAV users only,as satellite users and eavesdroppers have fixed access.We use aK×Kmatrix Π to denote the channel allocation matrix with entriesπkl ∈{0,1},whereπkl=1 denotes that UAV userkis scheduled at channell,andπkl=0 otherwise.We have the following constraints for fairness

We denoted the transmission power of UAVs as anN ×Kmatrix P with entriespnldenoting the transmission power of UAVnin channell.For convenience,we define the power matrix Pland power vector plin channellas

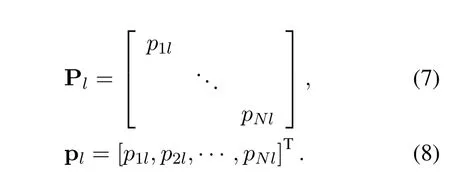
Due to the limited transmission power of each UAV,we have

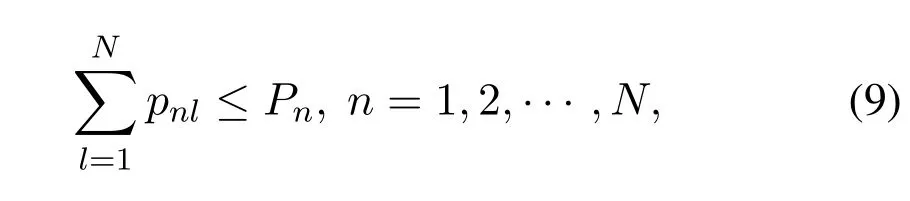
which means that the total transmission power of UAVnin different subchannels can not exceed its maximum transmission power,denoted asPn.

Noting that the satellite and UAVs share the same spectrum,we need to limit the interference from UAVs to satellite users.In order to save costs,we consider the average interference constraint as

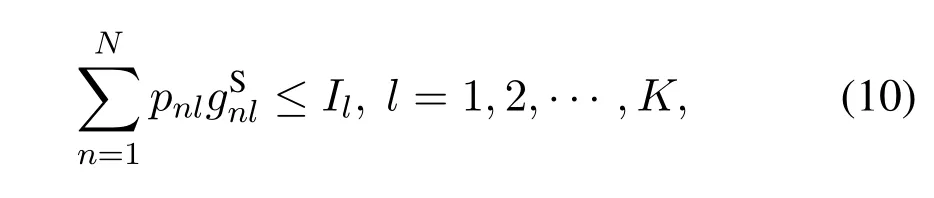
which means that the average interference from UAVs to satellite userlshould not exceed the thresholdIl.

The UAV swarm and UAV users form a distributed MIMO system.The MIMO capacity between the UAV swarm and UAV userkin channellcan be calculated as

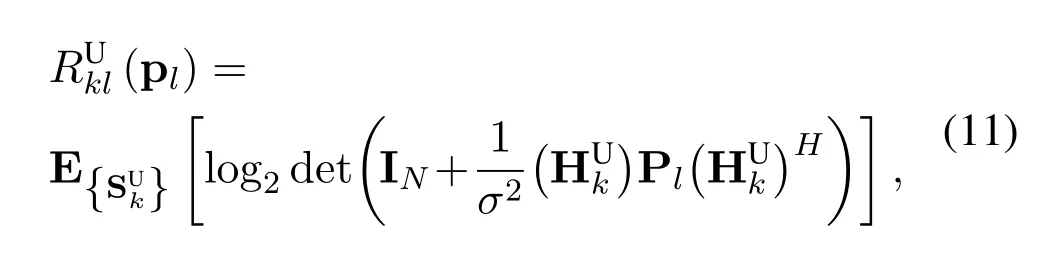
whereσ2represents the noise variance,INis theN×Nidentity matrix,anddenotes the expectation operator with respect to the small-scale matrix,which is modeled as a random matrix in(2).

Similarly,the channel capacity between the UAV swarm and eavesdropperlin channellis

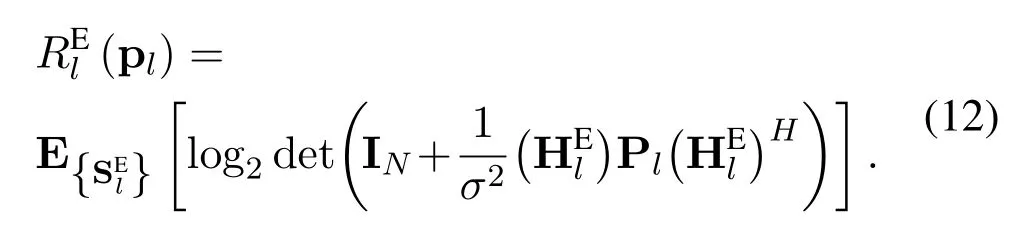
With(11)and(12),the average secrecy rate of UAV userkin channellis given by

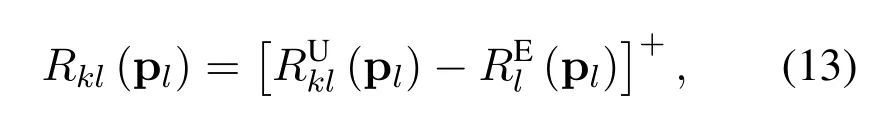
where [x]+≜max{x,0}.We can formulate the secrecy sum rateRof the system as

III.JOINT POWER AND CHANNEL ALLOCATION FOR SECRECY RATE MAXIMIZATION

3.1 Problem Formulation

Our goal is to maximize the secrecy sum rateRby jointly optimizing the UAVs’ transmission power P and the channel allocation scheme Π,under the power constraint in(9)and the interference constraint in(10).The optimization problem can be formulated as

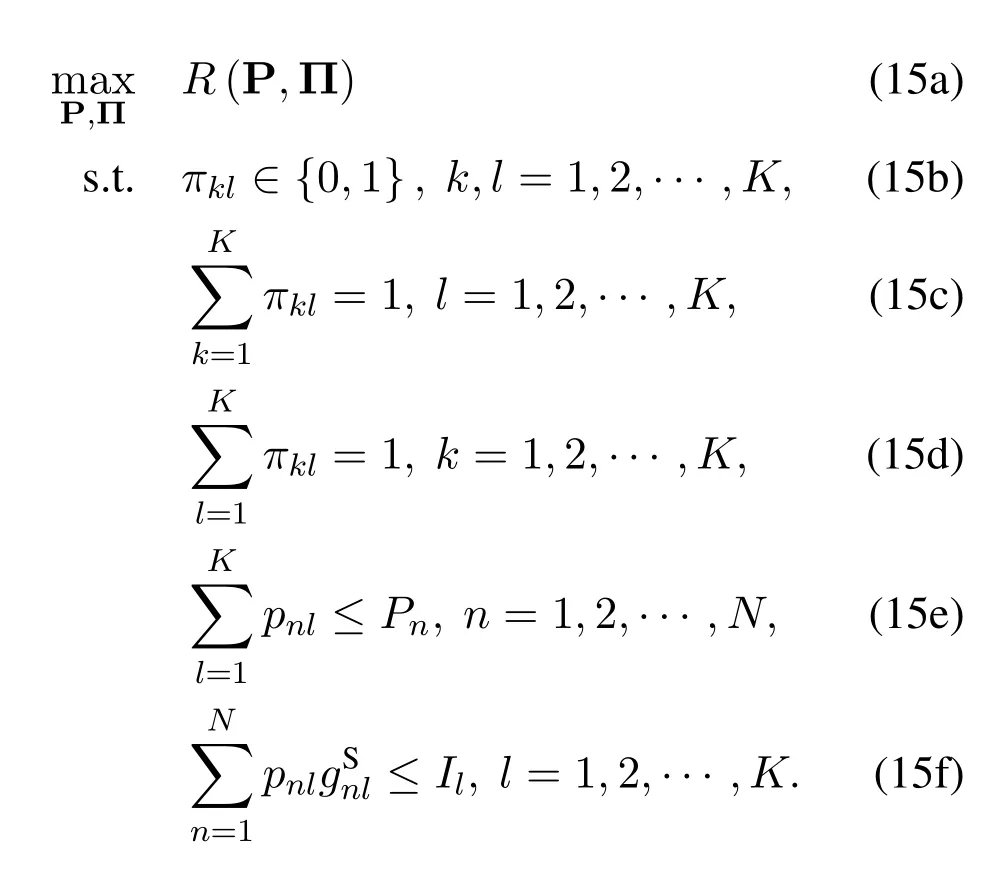
The optimization problem in (15) is an MINLP problem with a non-convex objective function,so its global optimal solution is difficult to obtain.Besides,the operator [·]+in (13) and the expectation operator E[·] in (11) and (12) make the objective function not smooth and in the form of integrals.It is worth noting that we have considered a similar problem in our previous work [1],where the transmission power constraint in (15e) is replaced with the power budget constraint for the UAV users.However,the coupling of the transmission power in different subchannels in constraint (15e) makes this problem more difficult to solve.Next,we will transform the problem into a more tractable form.

3.2 Problem Transformation

In this subsection,we transform the problem in (15)into an approximate max-min problem easier to solve.First,we have the following proposition that the operator [·]+in (13) can be removed directly without changing the optimal value.

Proposition 1.The optimal solution to the following problem is also optimal for(15).

Proof.See Appendix A.

Next,we approximate the objective function in(17) with a new function(P,Π,w,z) in a closed form,where w[w1,w2,···,wK]Tand z[z1,z2,···,zK]Tare auxiliary variables.The new objective function is formulated as

wherewl ≥0 andzl ≥0 satisfy the equations

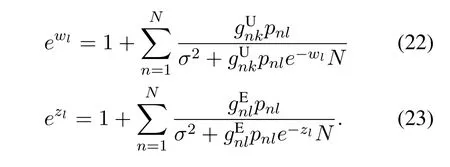
The approximation is based on random matrix theory,and its accuracy has been shown in [26] in detail.Similar to [26],by checking the derivatives ofwith respect towlandzlrespectively,we can find that the equations in(22)and(23)are equivalent to the proposition thatwlandzlare the minimum points of,respectively.As a result,we can transform (16) into the following max-min optimization problem.

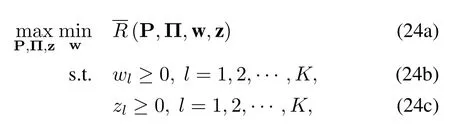
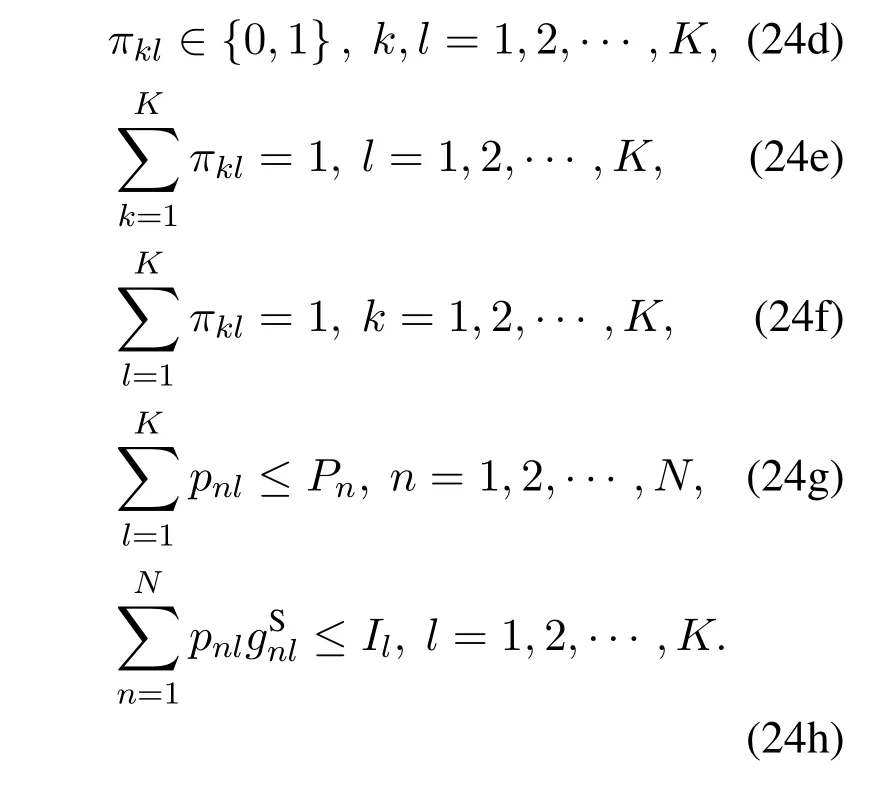
From(24),we can see that the complicated expectation operator is removed by introducing the optimization operations with respect to the auxiliary variables w and z.However,the nonconvexity and coupling of variables still make it challenging to solve(24).In particular,constraint(24g)couples the power in different subchannels.

3.3 Relaxing the Constraints Using Penalty Methods

In this subsection,we relax constraint (24g) with the penalty method.First,we introduce the auxiliary variables P′in the following problem

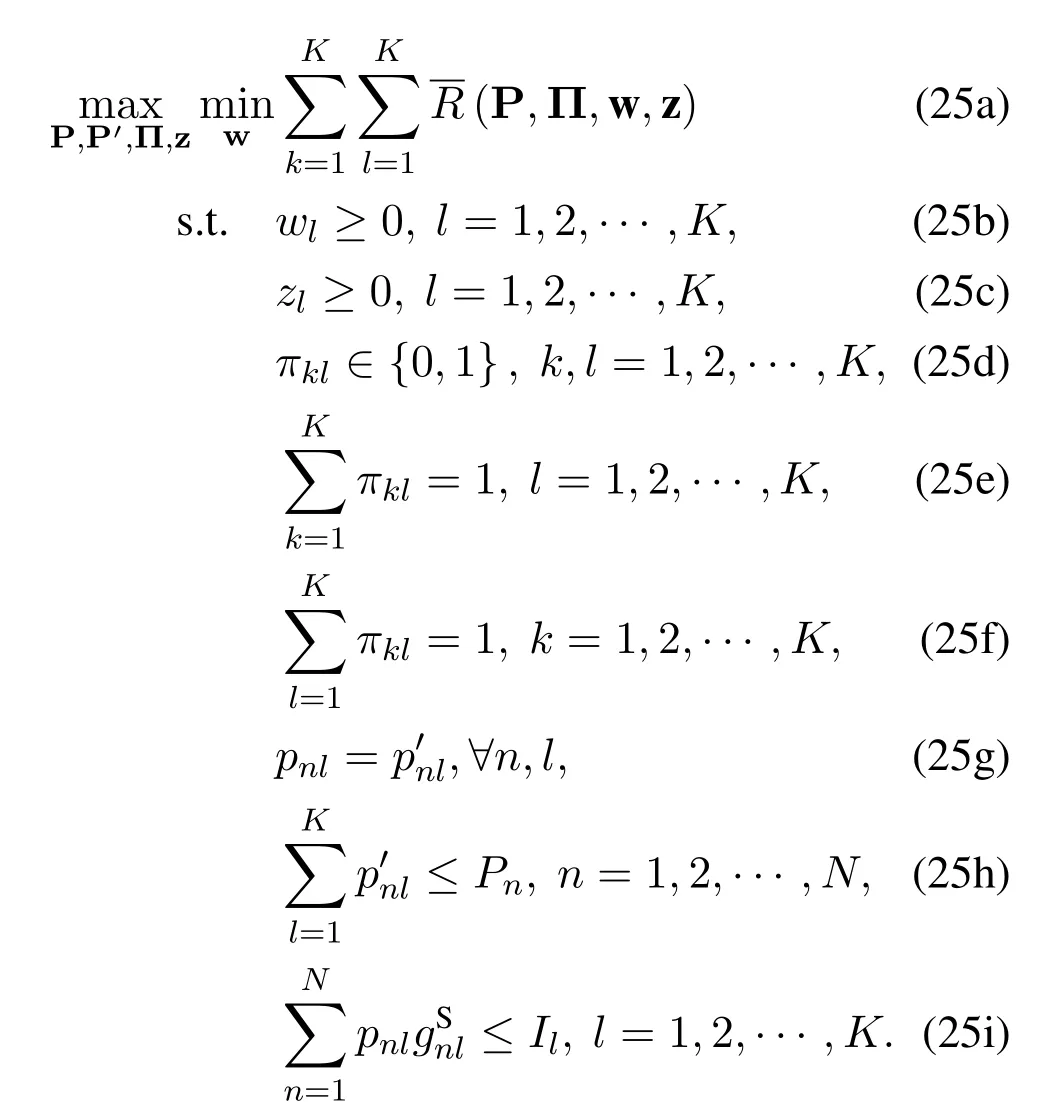
In problem (25),the constraint for P in (24g) is transformed into constraint(25h)for P′.Next,we relax the equality constraint (25g) by adding a penalty term to the objective function.We have the new problem as

whereϕ ＞0 is a penalty parameter that imposes a penalty for violating constraint (25g).Particularly,whenϕ →∞,problem(26)is equivalent to problem(25).After relaxation,the transmission power in different subchannels is not coupled in the constraints.However,problem (26) is still an MINLP problem with a non-convex objective function.

3.4 Problem Decomposition

For convenience,we denote the objective function in(26)asformulated as

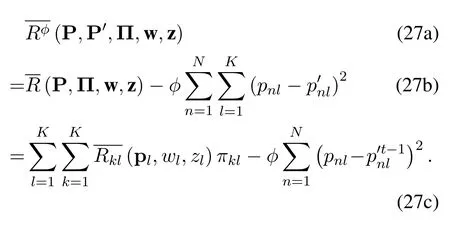
Problem (26) has a non-convex objection function and integer variables.To solve this problem,we decompose it into two subproblems,which are formulated as

wheretdenotes the iteration index.Problem(28)optimizes P,Π and w with fixed P′and z,which is an MINLP problem.Problem (29) optimizes P′and z with the other variables fixed.Problem(29)is a convex optimization problem,which can be solved efficiently with convex optimization tools.We solve problem(26)by solving(28)and(29)iteratively.The iterative algorithm will be described in subsection 3.5 in detail.

3.5 The Algorithm to Solve Problem(28)

Based on constraints(26e)and(26f),can be rewritten as

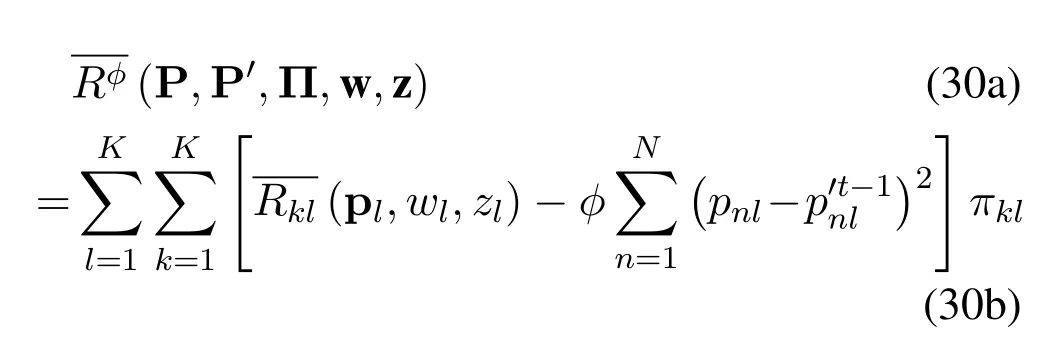
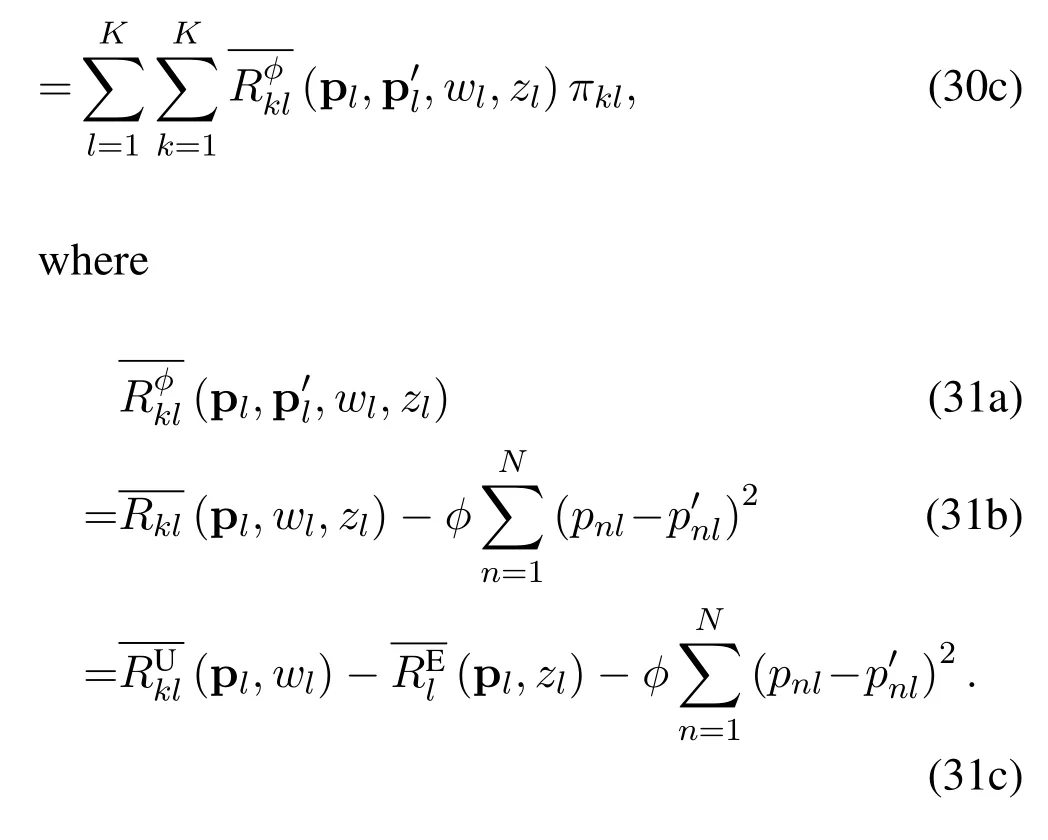
It can be proven thatis not concave with respect to P,which makes problem (28) difficult.We approximate it to a concave function with respect to P based on the first-order Taylor expansion ofThe expansion expression ofat a certain pointcan be formulated as

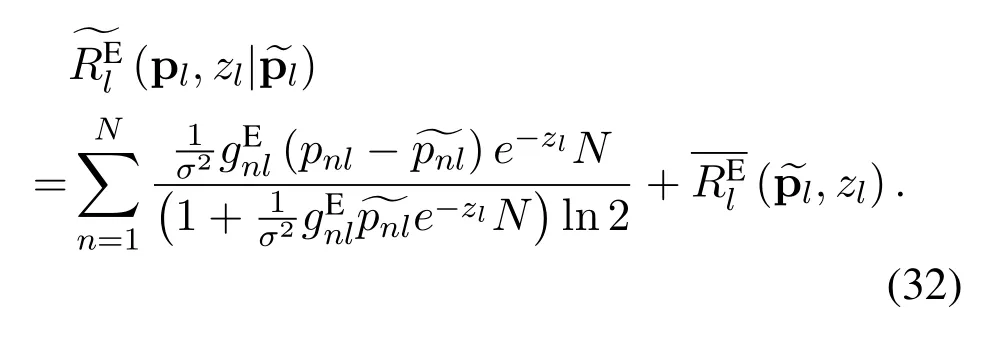
Based on(32),the approximation of,denoted as,is given by

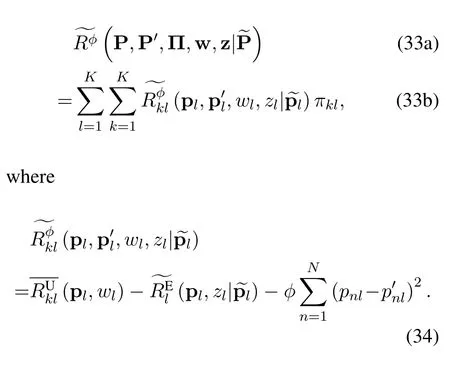
By expanding the objective function at pointwe approximate problem(28)as

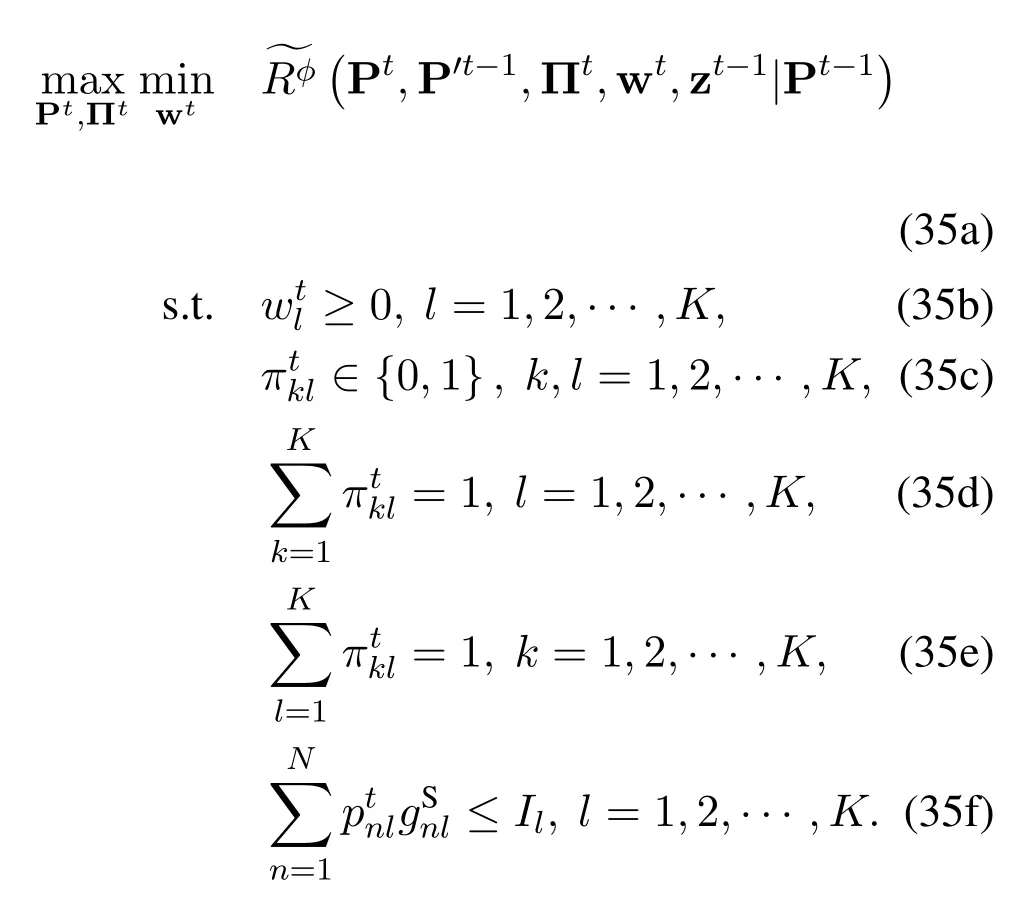
We solve problem (35) using the bipartite graph matching algorithm and the max-min optimization tool,as in our previous work[1].Noting that the coupling of the transmission power in different channels in the constraints has been removed via the penalty method,we can rewrite problem(35)as

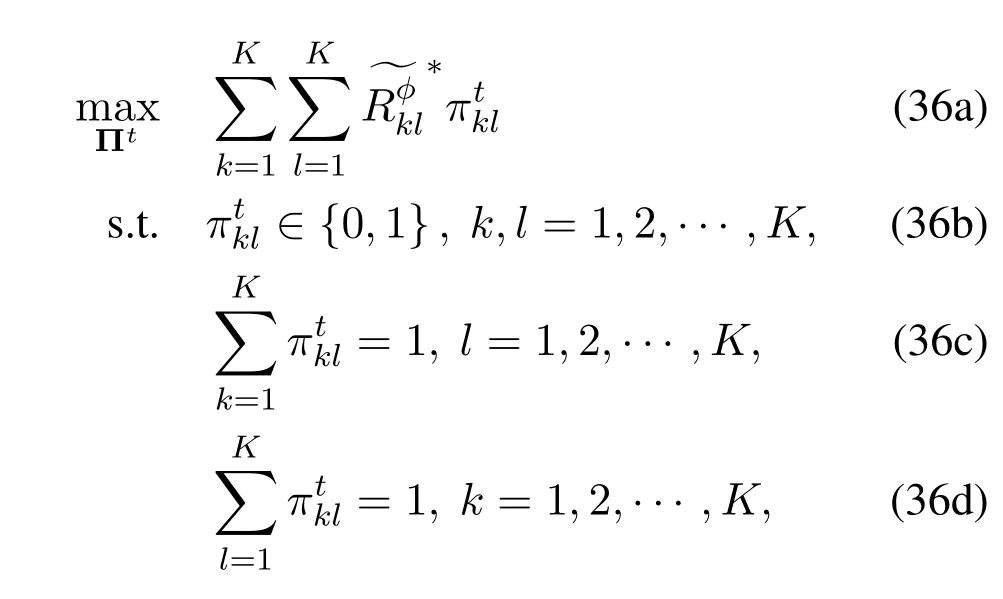
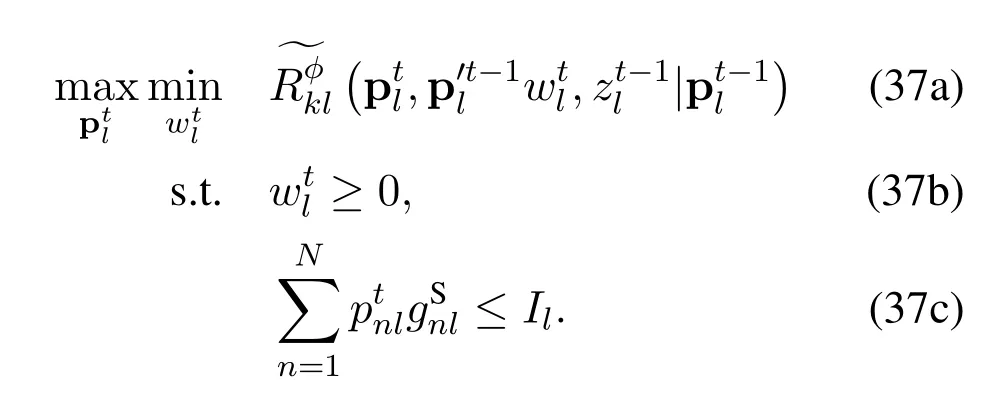
From (36) and (37),we can see that problem (36)only optimizes the channel allocation,while problem(37) only considers the power allocation in a single channel.Askandltraverse the set [1,2,···,K],there are a total ofK2subproblems in the form of problem (37).By decomposing problem (28) into a master problem(36)andN2subproblems in the form of(37),we eliminate the coupling between channel allocation Π and power allocation P.

With the objective function convex with respect toand concave with respect to,problem (37) can be solved efficiently by the max-min optimization tool.Next,we focus on the channel allocation problem in(36),which is a binary integer programming problem.We solve this problem based on the bipartite graph matching method[1].As shown in Figure 2,a bipartite graph is constructed corresponding to the channel allocation problem,where two node sets denote UAV users and channels respectively.The edge connecting UAV user nodekand channel nodeldenotes that UAV userkis scheduled at channell,i.e.,πkl=1,and its weight is set as.With this setup,we can see that the channel allocation problem (36) is equivalent to the maximum-weight matching problem of the bipartite graph,which is to find the best matching of the graph,in which the sum of the weights of the edges is maximized.We use the Kuhn-Munkres algorithm to solve this matching problem with a complexity ofO(K3) [27],which is much lower than the complexity ofO(K!) if we traverse all the channel allocation schemes.

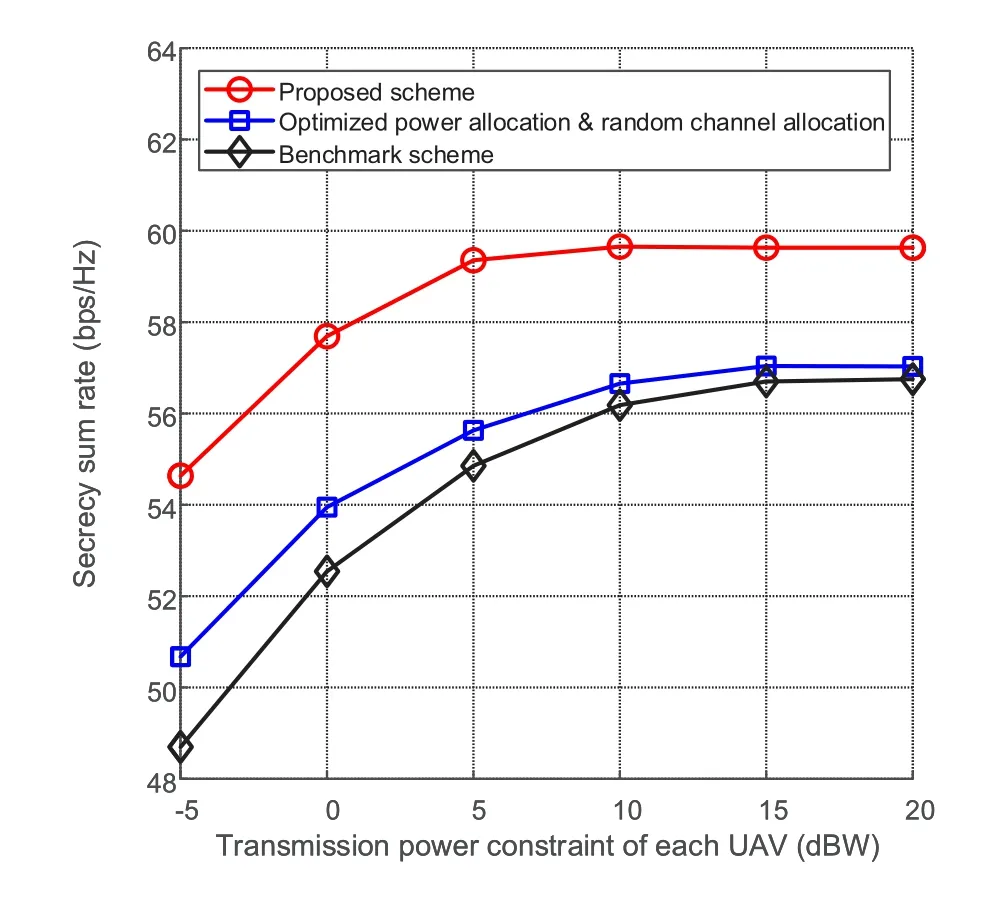
Figure 3. Secrecy sum rate achieved by different schemes with different transmission power constraints of each UAV.

By solving the master problem (36) and subproblems in (37),we can obtain the solution to problem(28)with Algorithm 1.

3.6 The Algorithm to Solve Problem(26)

We solve problem (26) by solving the two subproblems (28) and (29) iteratively,where (28) can be solved with Algorithm 1.It is easy to show that the objective function in(29)is jointly concave with respect to P′tand zt.Therefore,problem (29) is a convex optimization problem and can be solved efficiently by convex optimization tools such as CVX[28].

By solving problem (28) and (29) iteratively,we have Algorithm 2 to obtain a sub-optimal solution to problem(26).The following proposition demonstrates that Algorithm 2 is assured to converge.

Proposition 2.along with the iterations,i.e.,for any t ≥1,and Algorithm 2 is guaranteed to converge.Proof.See Appendix B.

It is worth noting that the penalty factorϕis a predetermined parameter in Algorithm 2.The selection ofϕwill influence the result of the algorithm.In subsection 3.7,we will focus on the selection ofϕ,and give an overall iterative algorithm to solve problem(24).

3.7 The Overall Algorithm

In this subsection,we focus on the penalty factorϕin the algorithm.As mentioned in Section III,ϕimposes a penalty for violating the constraint.Specifically,a smallϕimposes a slight penalty,which may cause constraint(24g)to be unsatisfied.While a largeϕmay draw too much attention to the penalty term and lead to an unsatisfactory secrecy rate.Thus,special attention should be given to the selection of the penalty factorϕ.

Inspired by [29,30],we propose an iterative algorithm to solve problem (24) as Algorithm 3,where we change the penalty factorϕduring each iteration.Specifically,we initializeϕwith a small value to achieve a high secrecy sum rate.During each iteration,we increaseϕat a fixed ratecuntil a large boundϕmaxis reached,which will force constraint(24g)to be satisfied.As Algorithm 2 is guaranteed to converge,Algorithm 3 is guaranteed to converge whenϕ=ϕmax.

Algorithm 3 is heuristic and its computational complexity is related to the number of iterations and the initial point.Next,we will evaluate its performance and convergence rate via simulations.

IV.SIMULATION RESULTS AND DISCUSSION

In this section,the simulation results are provided to evaluate the performance of the proposed scheme.We suppose that UAVs are uniformly distributed in a circle with a radius of 1000 m,and the UAV users and the satellite users are uniformly distributed in a circle with a radius of 5000 m.Eavesdroppers are distributed in an annulus with an inner radius of 5000 m and an outside radius of 6000 m to hide themselves.The height of the UAVs is 1000 m.The number of UAVs is set asN=5,and the number of subchannels is set asK=10.The other parameters are set as follows:ϕ0=1,r=5,ϕmax=100000,ϵ0=1e-8,f=2.4 GHz,c=3×108m/s,a=5.0188,b=0.3511[25],andσ2=-107 dBm.The(ηLOS,ηNLOS)pair is set as(1.0,20),according to[25].We use CVX toolbox for MATLAB with sdpt3 solver to solve the optimization problem.

In order to verify the performance of the proposed scheme,we compare the following three schemes:

• Proposed scheme:Joint optimization of the power allocation and channel allocation.

• Scheme in [22]: Optimization of only the power allocation with random channel allocation.

• Benchmark scheme: Equal power allocation with random channel allocation.

As the last two schemes do not consider the interference of satellite users,if the interference of any satellite user exceeds the threshold,we reduce the transmission power in the corresponding channel to satisfy the constraint.In order to reduce the influence of random factors,we average the results of ten snapshots as the final result for the last two schemes.

Figure 3 shows the secrecy sum rate versus the transmission power constraint for different schemes when the interference threshold is set asIl=-70 dBm.The figure shows that when the maximum power of a UAV is lower than 15 dBW,the secrecy sum rate increases with the power.However,it becomes saturated when the maximum power is over 15 dBW.This can be explained as follows.When the maximum power is low,as the maximum transmission power of UAVs increases,more power can be used in communication,which results in an increasing secrecy sum rate.When the maximum power is sufficiently large,the transmission power is mainly limited by the interference threshold.It can also be seen that the secrecy sum rate achieved by the proposed scheme is higher than those of the conventional schemes under all conditions,which verifies the superiority of the proposed scheme.The reason is that the proposed scheme can allocate more power to a channel with good conditions,while the other schemes select channels randomly.In addition,it can be seen from the figure that the performance gap between the second scheme and the benchmark scheme becomes smaller as the maximum power increases.In particular,when the maximum power is sufficiently large,the secrecy rates achieved by the two schemes become very close.This shows that the effect of power allocation becomes not so significant when the maximum power is large,which suggests that we can pay more attention to channel allocation when the maximum transmit power is large enough.

Figure 4 illustrates the sum secrecy rate versus the interference threshold withPn=15 dBW.Similarly,we can see that the secrecy rate increases withIlwhenIlis below-70 dBm.This is because more transmission power could be used with a larger interference threshold.Nevertheless,when the interference threshold is sufficiently large,the secrecy rate becomes saturated due to the power constraint.

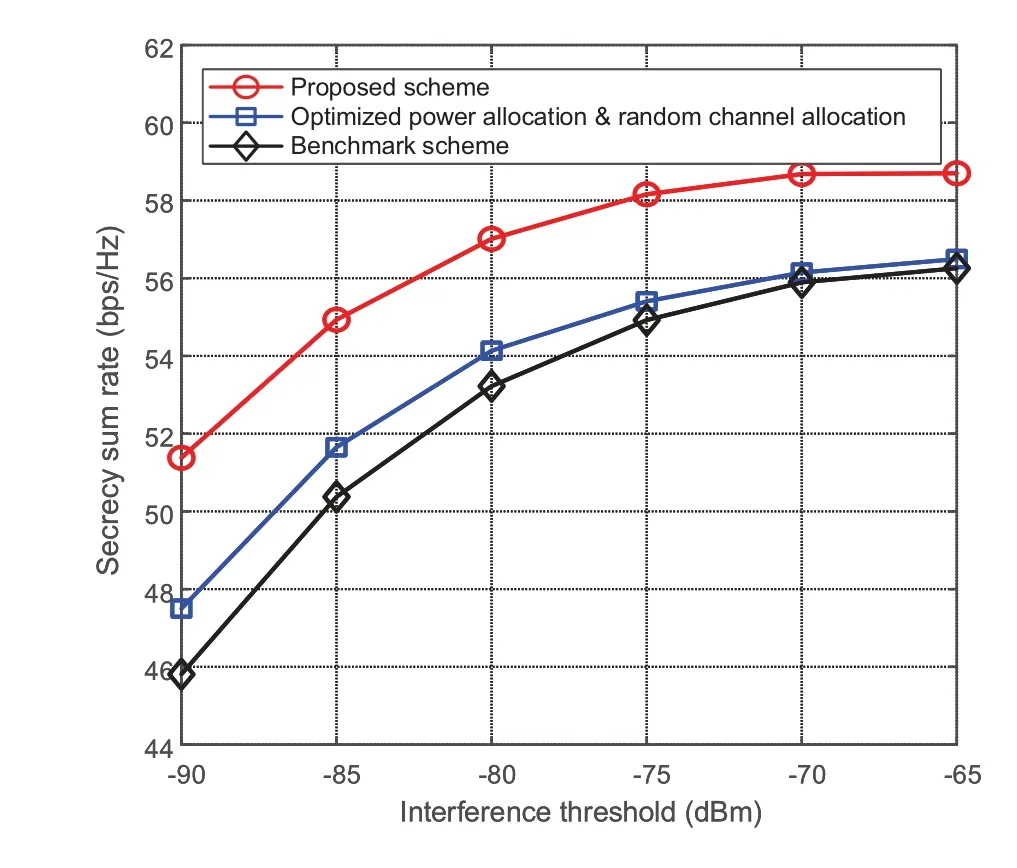
Figure 4. Secrecy sum rate achieved by different schemes with different interference thresholds.

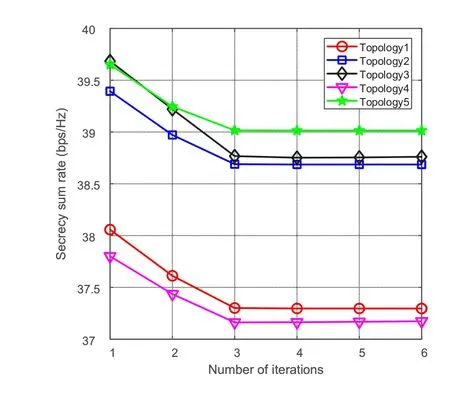
Figure 5. Secrecy sum rate during the iterations for 5 randomly-selected system topologies.

In Figure 5,we present the convergence speed of our proposed scheme for 5 randomly-generated system topologies.The maximum transmission power of UAVs is set asPn=10 dBW,and the interference threshold is set asIl=-60 dB.The results show that the proposed method can converge within 3 iterations,which verifies the convergence performance of our proposed scheme.It is worth noting that for each system topology,the secrecy sum rate decreases as the iteration proceeds.This is because we initializeϕwith a small value,which imposes a slight penalty if the interference constraint is not satisfied and leads to a large initial secrecy rate.As the penalty factor increases during the iterations,the solution needs to satisfy the interference constraint,which makes the secrecy rate decrease.

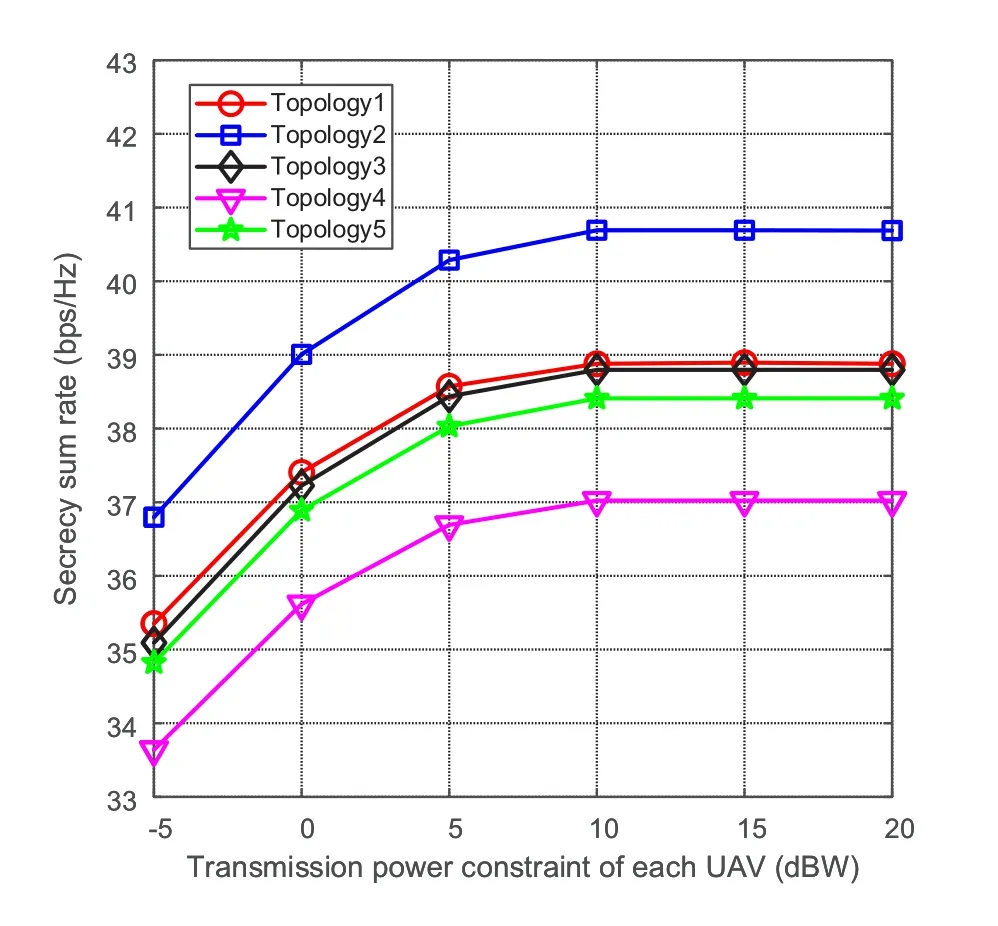
Figure 6. Secrecy sum rate with different power constraints for 5 randomly-selected system topologies.

Figure 6 illustrates the secrecy sum rate achieved by our proposed method with different power constraints for 5 randomly-generated UAV positions.The interference threshold is set as-70 dBm.We can see that the secrecy sum rate changes with the change of the positions of UAVs,and the range of change of the secrecy sum rate is approximately 4 bps/Hz.This is because the channels between UAVs and the ground nodes will change as the positions of UAVs change,resulting in different security performance.Thus,the positions of UAVs are important in a cognitive satellite-UAV network.

Figure 7 compares the secrecy sum rate versus the transmission power constraint in urban environments and suburban environments,where the urban environment parameters are set asηLOS=1,ηnLOS=20,a=9.6101 andb=0.1592 according to[31].From the figure,we can find that the secrecy rate in urban environments is higher than the secrecy rate in suburban environments.In urban environments,both the legitimate channels and the eavesdropping channels exhibit worse fading compared to the suburban case.However,the elevation of the eavesdroppers is higher than that of the UAV users,which leads to a higher nLOS probability.The channel capacity of the eavesdropping channels decreases faster,which causes a higher secrecy rate in urban environments.Therefore,the security problem is more serious in rural areas and deserves more attention.

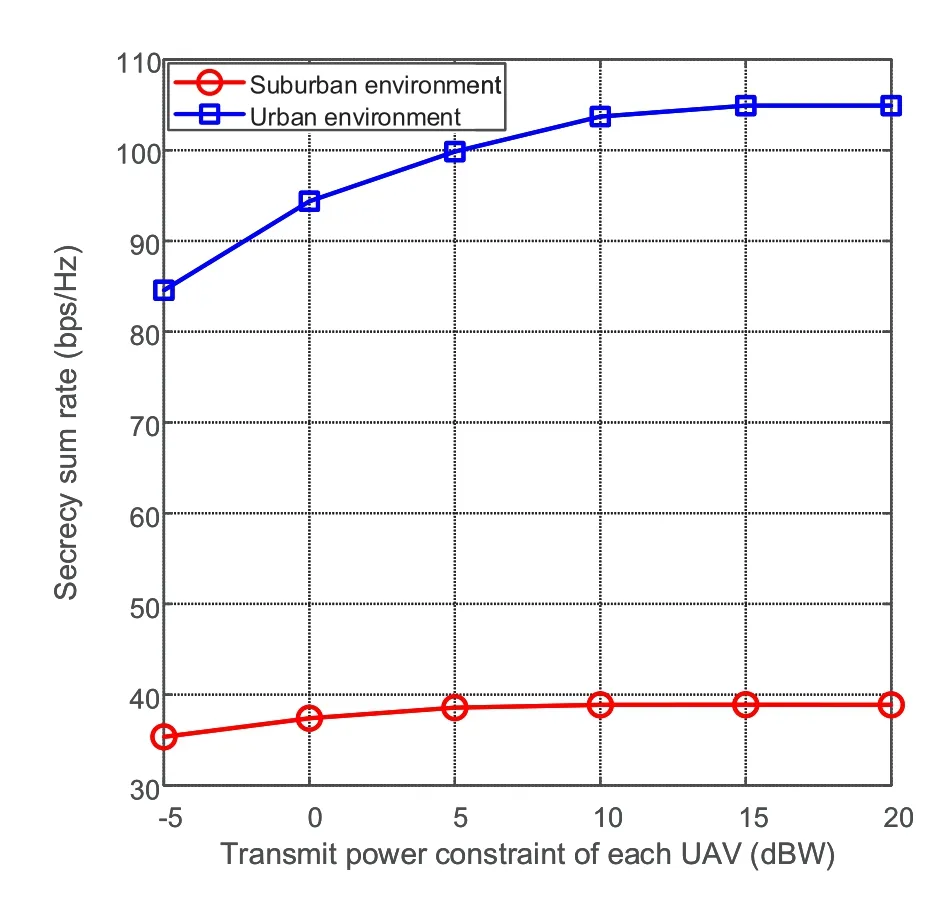
Figure 7. Secrecy sum rate with different power constraints in urban scenarios.

V.CONCLUSION

In this paper,we have investigated the PLS problem in a cognitive satellite-UAV network.Specifically,we have maximized the secrecy sum rate by jointly optimizing the power allocation and channel allocation of the UAV swarm.The optimization problem is an MINLP problem with a non-convex objective function.We have solved it with an iterative algorithm by using the penalty method,the bipartite graph matching algorithm and max-min optimization tool.The simulation results have been provided to demonstrate the superiority of the proposed scheme.

ACKNOWLEDGEMENT

This work was supported in part by the National Key Research and Development Program of China under Grant 2020YFA0 711301;in part by the National Natural Science Foundation of China under Grant U22A2002 and Grant 61922049.

APPENDIX

A Proof of Proposition 1

We denote the optimal values ofRandin(15)and(16)asL1andL2respectively.As(15)and(16)have the same feasible set andR(P,Π)≥ˆR(P,Π)holds for any (P,Π),we haveL1≥L2.Next,we prove thatL2≥L1also holds.

Assuming that (P*,Π*) is the solution to (15),we construct a feasible solution to (16),denoted as,as follows.

First we define the auxiliary variables as

B Proof of Proposition 2

Based on(29),we have

As the Taylor expansion approximation does not change the form of w,the optimal w*to the approximate problem(35)is also optimal to the primal form if P and Π are fixed,i.e.

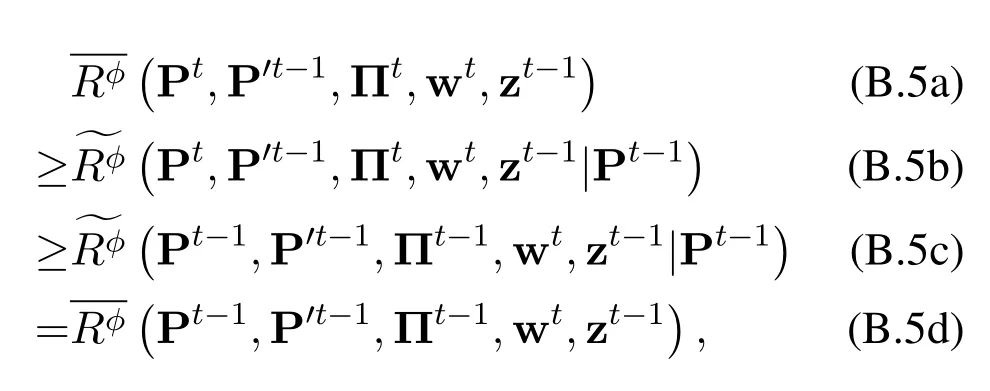
where(B.5c)holds because Ptand Πtmaximize the approximation ofin(35).

Therefore,we can obtain

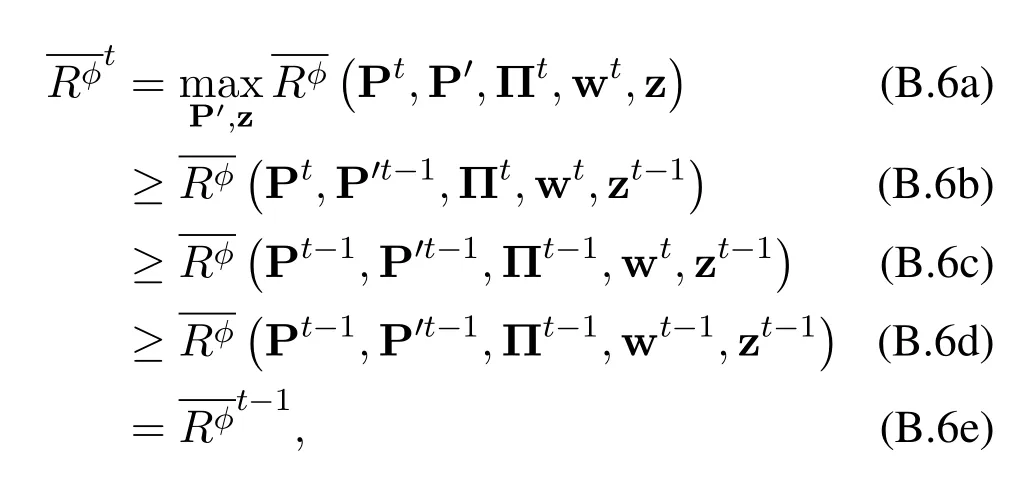
where (B.6c) follows from (B.5),and (B.6d) follows from (B.3).Therefore,does not decrease during each iteration,so Algorithm 2 is guaranteed to converge.