Deep Learning Aided SCL Decoding of Polar Codes with Shifted-Pruning

Yang Lu ,Mingmin Zhao ,Ming Lei ,Chan Wang,* ,Minjian Zhao

1 College of Information Science and Electronic Engineering,Zhejiang University,Hangzhou 310027,China

2 Zhejiang Provincial Key Laboratory of Information Processing,Communication and Networking (IPCAN),Hangzhou 310027,China

Abstract: Recently,a generalized successive cancellation list (SCL) decoder implemented with shiftedpruning(SP)scheme,namely the SCL-SP-ω decoder,is presented for polar codes,which is able to shift the pruning window at most ω times during each SCL re-decoding attempt to prevent the correct path from being eliminated.The candidate positions for applying the SP scheme are selected by a shifting metric based on the probability that the elimination occurs.However,the number of exponential/logarithm operations involved in the SCL-SP-ω decoder grows linearly with the number of information bits and list size,which leads to high computational complexity.In this paper,we present a detailed analysis of the SCL-SP-ω decoder in terms of the decoding performance and complexity,which unveils that the choice of the shifting metric is essential for improving the decoding performance and reducing the re-decoding attempts simultaneously.Then,we introduce a simplified metric derived from the path metric (PM) domain,and a custom-tailored deep learning (DL) network is further designed to enhance the efficiency of the proposed simplified metric.The proposed metrics are both free of transcendental functions and hence,are more hardware-friendly than the existing metrics.Simulation results show that the proposed DL-aided metric provides the best error correction performance as comparison with the state of the art.

Keywords: polar codes;successive cancellation list decoding;deep learning;shifted-pruning;path metric

I.INTRODUCTION

Polar codes are a type of structural channel coding schemes proposed by Arıkan [1],which is theoretically proven to reach the Shannon capacity limit of binary-input discrete memoryless channels (BIDMCs) by using the efficient successive cancellation (SC) decoding algorithm.Due to the provable capacity-achieving property,the fifth generation of cellular mobile communications (5G) standard have selected polar codes as the channel coding scheme of the enhanced mobile broadband(eMBB)control channel.However,for short to moderate code lengths,the error correction performance of polar codes under SC decoding is inferior to the low density parity check(LDPC)codes[2]and Turbo codes[3].Based on the SC decoding algorithm,a successive cancellation list(SCL) decoder was introduced in [4] to improve the error correction performance of polar codes by reserving a list of possible candidate paths at each decoding step.Besides,with the aid of cyclic redundancy check(CRC)bits concatenated to polar codes,the decoding performance of the SCL decoder can be further enhanced [4,5].In particular,the CRC-assisted SCL (CA-SCL) decoder can achieve superior performance that is comparable to the maximum likelihood(ML) decoder at the high signal-to-noise ratio (SNR)regime.However,the performance gain of the CASCL decoder gradually diminishes with the increasing of the list sizeL,while the corresponding memory cost and computational complexity increase withL.

To enhance the error correction performance of the SC and SCL decoding algorithms,decoders based on the bit-flipping algorithm are further presented in[6-11].The principle of bit-flipping is to flip the bits with low reliability in additional re-decoding attempts in case the standard SC or SCL decoding output fails the CRC,hence improving the error correction performance.The research on bit-flipping-based decoders strives in two aspects,one is to propose new bitflipping strategies in SC or SCL decoding,and the other is to determine the positions for bit-flipping.In the bit-flipping-based SC decoder,e.g.,the SC-Flip decoder [6],the first erroneous bit caused by channel noise is flipped in new decoding attempts when the initial decoding fails,thus the error propagation issue caused by this erroneous bit can be avoided.While for the bit-flipping-based SCL decoder,the bitflipping strategy is actually flipping multiple paths for a chosen information bit.Note that in the standard SCL decoder,theLpaths with the smallest path metric (PM) values are preserved,while in the SCL-Flip decoder [10],a portion of the originally eliminated paths are preserved,thus making it possible to prevent the correct path from being discarded.Another bitflipping strategy proposed in [11] selects theLeliminated paths as new survival paths for all re-decoding attempts,which is able to produce a different codeword estimate as compared to the standard SCL decoding.It was shown in[11]that this method can reduce the number of re-decoding attempts and computational complexity.

Determining the appropriate positions for bitflipping is essential,and there are various works in the literature that provide different solutions[8,7,9,12].Specifically,the critical set(CS)approach proposed in[8] is a simple and popular way to provide a candidate set for bit-flipping.The CS involves the bit positions that are more likely to cause the first decoding error in SC decoding,thus invalid decoding attempts can be reduced significantly.With the assistance of the CS,the SCL-Flip decoder [10] can significantly outperform the CA-SCL decoder,at the expense of a few number of re-decoding attempts.However,the CS is not accurate for erroneous bit identification in SCL decoding as compared to that in SC decoding since the error distributions in these two decoding algorithms are different.Moreover,when adopting the CS approach,only a single bit is considered for flipping in each re-decoding attempt,which may limit the error correction performance.To alleviate these problems,the works [9,12] proposed to dynamically flip more than one bit in each re-decoding attempt,based on the analysis of the error distributions in SC or SCL decoding.Specifically,the work [9] presented a dynamic SC-Flip decoder with multiple bit flips,and a flipping metric was proposed to determine the flipping positions,where the log-likelihood ratios(LLRs)of the previously decoded information bits were exploited to evaluate the probability of a successful decoding.The work[12]introduced a generalized SCLFlip decoder,namely the SCL-Flip-ωdecoder,which is able to achieve state-of-the-art performance by flipping at mostωbits.However,most metrics mentioned above incur high computational complexity,as calculating them involves exponential and logarithmic operations and these operations are required for decoding each information bit.

Instead of correcting the erroneous bits through bitflipping,the work [13] proposed a new mechanism,namely shifted-pruning (SP),to prevent the correct path from being eliminated in SCL decoding.In particular,the main idea is to select the paths fromk+1 tok+Lout of the 2Lordered paths instead of the paths from 1 toL,wherekis the offset to shift the pruning window.Accordingly,a SCL-SP decoder was presented to avoid the elimination of the correct path during SCL decoding.Similar to the bit-flipping-based SCL decoders,the SCL-SP decoder performs SP on one of the bits from the CS in each re-decoding attempt in case the initial SCL decoding fails.It was shown in [13] that the SCL-SP decoder outperforms the SCL-Flip decoder[10]by around 0.3 dB at frame error rate(FER)10-2,and in the meantime the number of re-decoding attempts can be reduced.It is noteworthy that the bit-flipping strategy in [10] and [12] can be seen as a special case of the SP scheme by setting the shifting offsetkas the list size,i.e.,k=L,and thus the SCL-Flip-ωdecoder[12]is also referred to as the SCL-SP-ωdecoder in the following.However,the SCL-SP-ωdecoder suffers from high computational complexity,due to the re-decoding attempts and the calculation of the shifting metric.

In this work,we analyze the ideal decoding performance of the SCL-SP-ωdecoder,i.e.,the FER lower bound,as well as its complexity in terms of the number of decoding attempts.Moreover,two new metrics for shifting position identification are presented to release the computational burden of existing metrics without sacrificing the decoding performance much.To summarize,the main contributions of this work are listed as follows:

1.First,we present a detailed analysis of the SCLSP-ωdecoder,including the theoretical FER performance lower bound and the computational complexity.This analysis can serve as a reference for evaluating the effectiveness of the shifting metrics,which helps to further improve the SCL-SP-ωdecoder.

2.Second,a simplified shifting metric based on PM is proposed to determine the shifting positions.In particular,different from the two LLR-based metrics in [11] and the PM-based metric in [12],our proposed metric is free of costly transcendental function calculations and only involves simple addition/subtraction operations.Despite the fact that some approximations are employed in the proposed metric,numerical results show that the SCL-SP-1 decoder using the proposed simplified metric only incurs minor FER performance degradation as compared to the state of the art.

3.Finally,motivated by the recent success of exploiting deep learning(DL)techniques for decoding polar codes [14-21],we propose a DL-aided shifting metric.A deep neural network (DNN),whose weights are treated as the perturbation parameters,is presented to learn the correlation between the PM information and the bit positions where the elimination of the correct path may occur.Once the network is trained offline,the optimized perturbation parameters can be directly employed to calculate the shifting metric during decoding.Similar to the simplified metric mentioned above,the DL-aided metric is also free of transcendental functions and can be calculated based on the PMs on-the-fly.Simulation results show that the SCL-SP-ωdecoder using the proposed DL-aided metric can achieve state-of-theart FER performance yet with low computational complexity.

The rest of the paper is organized as follows.Section II presents the preliminaries of polar codes,CASCL,SCL-SP and SCL-SP-ωdecoders.In Section III,we derive the theoretical FER performance lower bound of the SCL-SP-ωdecoder and analyze its computational complexity.In Section IV,two shifting metrics are proposed,i.e.,the simplified metric and the DL-aided metric.In Section V,numerical results are provided to evaluate the performance of the proposed metrics and finally conclusions are drawn in Section VI.

The key abbreviations and notations used in this paper are summarized in Table 1 and Table 2,respectively.

Table 1. List of abbreviations.

Table 2. List of notations.

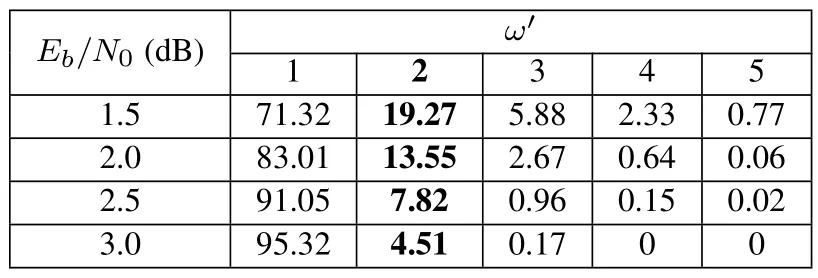
Table 3. Values of D(ω′)under different Eb/N0 points.

II.PRELIMINARIES

2.1 Polar Codes

A polar code of lengthN=2nwithKinformation bits andrCRC bits is defined asP(N,K,r).According to the channel polarization theory[1],Ksubchannels with higher reliability are selected to transmit information bits while the remainingN -Ksubchannels are devoted to transmitting frozen bits(usually set to 0).The set of information and frozen indices are denoted byAandAc,respectively,which are both known to the encoder and decoder.The binary message bits and transmitted polar codeword are respectively denoted by=(u1,u2,...,uN) and=(x1,x2,...,xN),whereis obtained by multiplying the message bitsby the generator matrixGN,i.e.,.GN=F⊗nis the polarizing matrix of sizeN ×N,whereis the base polarizing matrix and⊗denotes the Kronecker product.We assume that the codeword is transmitted over the additive white Gaussian noise (AWGN)channel with binary phase shift keying (BPSK) modulation,and the received signal vector corresponds tois denoted by=(y1,y2,...,yN).

2.2 SC and SCL Decoder

The SC decoder is a simple sub-optimal decoder for decoding polar codes,which is originally proposed in[1].In SC decoding,the estimate of each bitui,de-noted byi,is decided successively according to its LLRLi[22],i.e.,

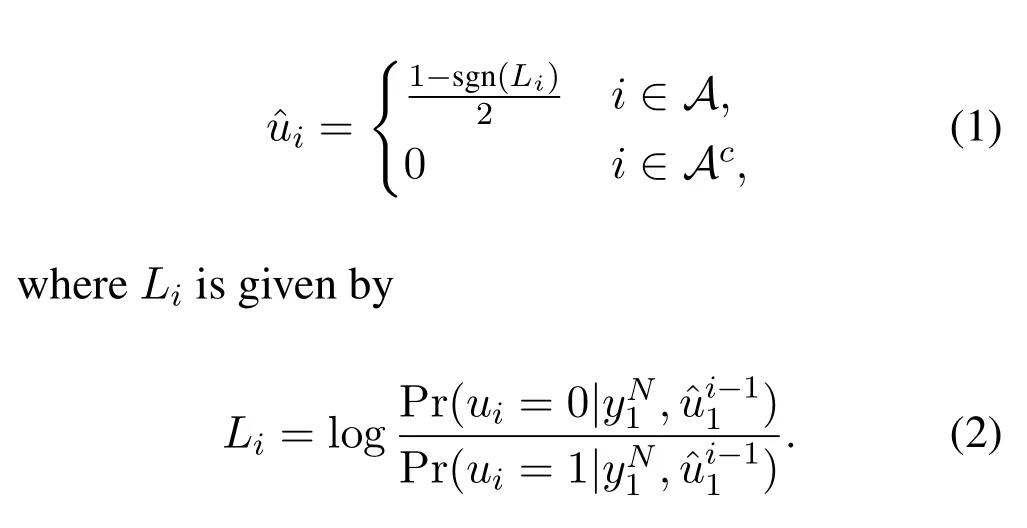
The SCL decoder estimates a bit considering both its possible values 0 and 1,by retainingLcandidate paths with the highest probability of correct decoding,so as to improve the error correction performance of SC decoding.Letdenote thel-th candidate path for decodingui,a path metricis introduced in the SCL decoder to evaluate the reliability of,which is expressed as

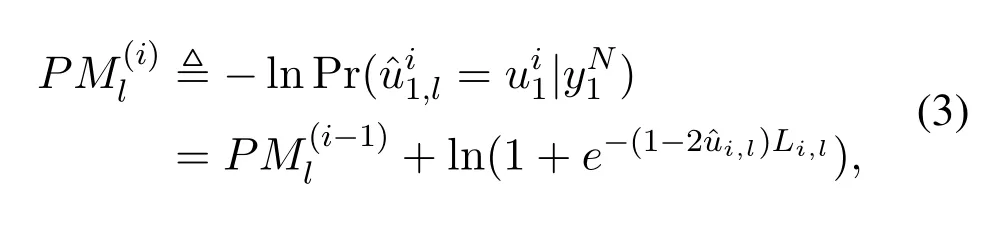
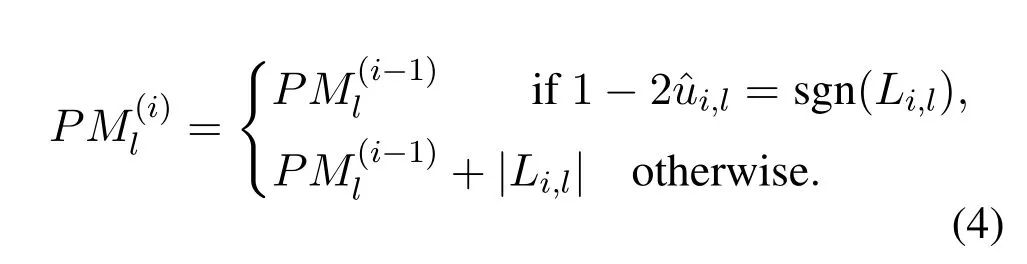
Without loss of generality,we assume that the 2Ltemporary paths are sorted in ascending order from＜··· ＜As can be observed from Eq.(3),the path with smaller PM value yields a higher probability to be correct.Thus,the SCL decoder eliminates unfavorable paths by selectingLpaths with the smallest PM values from the 2Lpaths,using the following path pruning scheme:

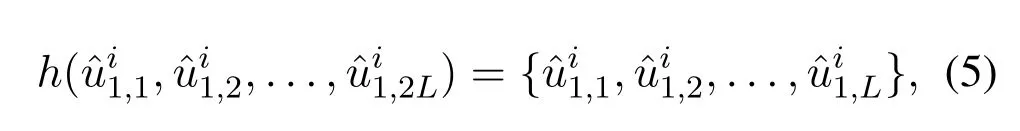
whereh(·)denotes the pruning function adopted in the SCL decoder.After allNbits are decoded,the path that passes the CRC with the smallest PM is claimed as the final decoding output.Otherwise,a decoding failure is claimed.

2.3 SCL-SP and SCL-SP-ω Decoder

In this subsection,we first give a brief introduction of the SP scheme and then present the SCL-SP and SCL-SP-ωdecoders.The SP scheme proposed in[13]makes a compromise between reservingLpaths with the smallest PMs in standard SCL decoder and reservingLpaths with the largest PMs as in the bit-flippingbased decoders[11,12],by shifting the pruning window by an offsetkranged from 0 toLto prevent the correct path from being eliminated.Figure 1 gives an example of the SP window with an offsetk=2 and list sizeL=4,where the green block represents the correct path,while the blue and red ones represent the reserved and discarded paths,respectively.

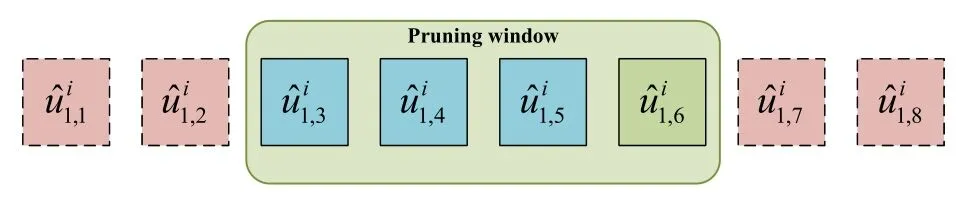
Figure 1. Shifted-pruning scheme(L=4 and k=2).

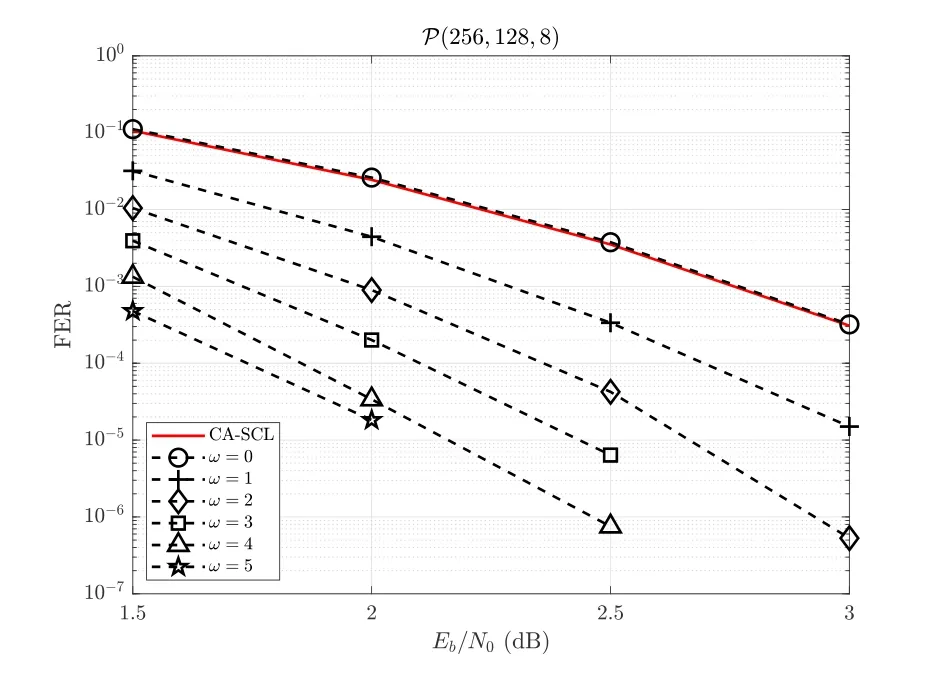
Figure 2. FER performance lower bound of the SCL-SP-ω decoder with L=8.

The SCL-SP decoder [13] can be regarded as a generalized SCL-Filp decoder by replacing the bitflipping strategy with the SP scheme,and the shifting positions are determined according to the CS [8](also referred to as the static CS).In this decoder,a standard SCL decoding is performed first,if the decoding fails,which indicates that the correct path is eliminated in this decoding process,extra re-decoding attempts (with a maximum numberT)are performed until one of the decoding output verifies the CRC.Note that in each re-decoding attempt,only one of the bit positions in the static CS(denoted bySstatic)is selected and the paths with indices fromktok+Lare retained.The remaining bits are still decoded by the standard SCL decoding.The corresponding pruning schemeh′(·)can be expressed as

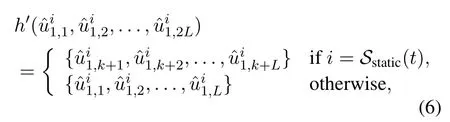
where 1≤t ≤Tis the re-decoding attempt index.

The SCL-SP-ωdecoder improves the decoding performance of the SCL-SP decoder by performing the SP scheme on up toωbits[12],instead of only shifting a single bit.The corresponding decoding process begins with an initial SCL decoding attempt,followed byωsteps of re-decoding attempts,and an incremental numbers of shifts are performed recursively in each step until no errors are detected by the CRC detector or the maximum number of re-decoding attempts is reached.1For theω′-th step(1≤ω′ ≤ω),the SCL decoding that shiftsω′bits will be performed for a maximum number ofT(ω′)times.The decoder will proceed to the(ω′+1)-th step if all the decoding outputs in theω′-th step fail the CRC.Therefore,the maximum number of re-decoding attempts in the SCL-SP-ωdecoder isdenote the set composed of all the candidate sets for shiftingω′bits,whererepresent thet-th candidate shifting set and theω′-th shifting position in,respectively.Then,for thet-th redecoding attempt in theω′-th step,the elements inare chosen as the shifting positions.Besides,it is noteworthy that several possible shifting positionsit,ω′+1can be derived based on a certain shifting metric(denoted byM),and the candidate shifting set forthe next step can be generated by concatenating withit,ω′+1that has the largest shifting metric value.This means that the decoding process of the SCL-SPωdecoder is based on a breadth-first tree search for the nested shifting bit positions.Therefore,is recursively generated based onand the shifting metric calculated during the re-decoding attempts of the previous step.2

When the bit being decoded is a frozen bit or the number of decoding paths is no more thanL,the correct path will not be eliminated and thus it is not necessary to conduct the SP operation in these cases.Consequently,the set of eligible shifting positions can be defined asA*=AA0,whereA0denotes the set containing the smallest log2Lbit indices inA.Then,for any shifting setE ⊆A*,the pruning function with regard toEis given by

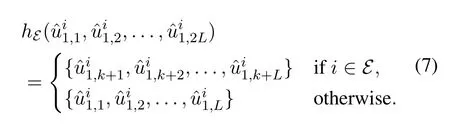
It can be seen from Eq.(7) that the SCL-Flip-ωdecoder can be seen as a special case of the SCL-SPωdecoder whenk=L.We note that new redecoding attempts in the SCL-SP-ωdecoder differ from the standard SCL decoding only in the pruning scheme,hence we use the notation SCL()to represent them in the following,and whenE=∅,SCL()reduces to the standard SCL decoding.

Take the SCL-SP-2 decoder as an example,the detailed decoding process is shown in Algorithm 1.As can be seen,a standard SCL decoding attempt without bit shifting is performed first (lines 2-7),followed byT(1)attempts of SCL decoding with single bit shifting (lines 9-20) if the initial decoding fails.3Different from the re-decoding attempts in the first step,each re-decoding attempt in the second step has two degrees of freedom with regard to the choice of the first and second shifting positions.In the first step,if the current re-decoding attempt index does not exceedT(2,1),i.e.,t1＜T(2,1),T(2,2)shifting sets each contain two nested shifting bit positions are generated and appended to(lines 21-27).The first nested bit of the shifting set is derived based on the current redecoding attempt,while the second one is determined by the calculated shifting metric.In line 22,a number ofT(2,2)candidate bits,i.e.,{i1,2,i2,2,...,iT(2,2),2},are determined according to the shifting metric values,and then each of them are concatenated with the first nested bit to construct a new shifting setEfor the second step (line 24).Then,is updated by appending these shifting sets in order (line 25).Finally,in case all the decoding outputs of the first step fail the CRC,a maximum numberT(2)of redecoding attempts with two bits shifting are further performed (lines 29-39) in case all the decoding outputs of the previous step fail the CRC,whereT(2)satisfiesT(2)=T(2,1)T(2,2).

III.ANALYSIS OF THE SCL-SP-ω DECODER

In this section,the theoretical FER performance lower bound of the SCL-SP-ωdecoder is provided,and its computational complexity is analyzed.In particular,we show that the performance lower bound and complexity are both closely related to some key parameters,including the probability of successful decoding and the probability that the correct path is eliminated.These key parameters can provide us guidelines to further improve the performance of the SCL-SP-ωdecoder and in the meantime reduce its decoding complexity.

3.1 FER Performance Lower Bound

Following[7]and[9],we use the expressionnoise realizationto represent the channel noise that corrupts the received signal.To correct a noise realization,an oracle-assisted SCL decoder implemented with the SP scheme is introduced first,namely the OA-SCL-SP decoder.This decoder differs from the standard SCL decoder only in the pruning scheme,i.e.,it can always correct the decoding errors in a genie-aided manner and the corresponding oracle-assisted pruning function can be expressed as

DefineD(ω′) as the probability that the noise realization is of orderω′,i.e.,D(ω′) ≜ Pr(ωy=ω′|ωy ＞0).In other words,D(ω′) represents the frequency thatωshifts are required by the OA-SCLSP decoder.Table 3 shows the values ofD(ω′)under differentEb/N0points,which are obtained when decodingP(256,128,8) withL=8.One can observe that most of the decoding failures are caused by order-1 noise realizations,accounting for about 85% of all the decoding failures in average.Besides,D(2) exceeds 10%atEb/N0=1.5 and 2.0 dB,which means that there are a lot of unavoidable decoding failures in the SCL-SP-1 decoder even for the best case that the first elimination has already been avoided by the SP scheme.Therefore,by shifting one more bits,there is a good chance that the SCL-SP-2 decoder can achieve much better performance than the SCL-SP-1 decoder.

In order to identify a tight FER lower bound of the SCL-SP-ωdecoder,we investigate two conditions that a successful decoding needs as the noise realization changes,which are listed as follows:

1.For any noise realization of orderωy ≤ω,the shifting setEyis included in

2.There is no CRC collision during the decoding,i.e.,no earlier erroneous decoding output verifies the CRC before running SCL(,A,Ey).

Once condition 1 is satisfied,then we can say that a noise realization of orderωy ≤ωis corrected by the SCL-SP-ωdecoder.Further,an ideal SCL-SPωdecoder (denoted by iSCL-SP-ω) is claimed if the above two conditions are both satisfied.Then,it can be inferred that a noise realization of orderωy ≤ωcan always be successfully corrected by the iSCLSP-ωdecoder,while the decoding will fail for anyωy ＞ω.Consequently,the FER of the iSCL-SPωdecoder caused only by noise realizations of orderωy ＞ωprovides a lower bound for the SCL-SP-ωdecoder.Accordingly,the FER lower bound is given by

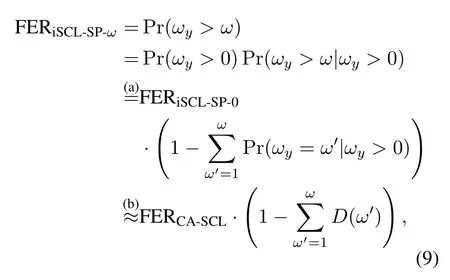
where FERiSCL-SP-ωand FERCA-SCLdenote the FER of the iSCL-SP-ωand CA-SCL decoders,respectively,(a) holds due to the definition of FER,i.e.,FERiSCL-SP-0=Pr(ωy ＞0),and (b) is obtained by replacing FERiSCL-SP-0with FERCA-SCLas we assume that the CRC collision probability is negligible in one decoding attempt.4

We note that the ideal iSCL-SP-ωdecoder can be obtained by restricting the maximum number of shifts in the OA-SCL-SP decoder toω.To validate the analysis in Eq.(9),Figure 2 depicts the actual FER lower bound of the SCL-SP-ωdecoder obtained via running the iSCL-SP-ωdecoder,with different values ofω.In this figure,the FER performance of the standard CASCL decoder is also provided for comparison.As can be seen,the FER lower bound provided by the iSCLSP-0 decoder is almost identical to that of the CA-SCL decoder despite the imperfect CRC.This implies that it is reasonable to neglect the probability of getting a CRC collision in one SCL decoding attempt and the approximation in Eq.(9) is quite tight.It is also observed that the iSCL-SP-ωdecoder (ω ≥1) exhibits significant SNR gains as compared to the CA-SCL decoder,varying from 0.5 dB(ω=1)to 1.5 dB(ω=5),at FER=10-4.Besides,the SNR gain is significant whenω=1,2 and gradually diminishes with the increasing ofω,which indicates that choosingω=2 is already sufficiently good as compared to the CA-SCL decoder in terms of FER performance.

Based on the analysis above,we now further investigate the differences between the FER lower bound and the FER achieved by the SCL-SP-ωdecoder.First,the FER of the SCL-SP-ωdecoder can be expressed as follows by resorting to the definition of FER:

where Pr(decoding failure|ωy=0) represents the probability of getting a CRC collision in the initial SCL decoding,which is close to 0 as we assume that there is no CRC collision in the initial SCL decoding.Moreover,letSM(ω′,T′) denote the probability that a received codeword corrupted by an orderω′(ω′ ＞0) noise realization is successfully decoded withinT′re-decoding attempts by the SCLSP-ωdecoder,with a chosen shifting metricM,i.e.,SM(ω′,T′) ≜Pr(decoding success|ωy=ω′).We haveSM(ω′,T′)=0 for anyω′ ＞ω.Accordingly,the FER of the SCL-SP-ωdecoder can be approximated by

From Eq.(11),it is observed that the FER performance gap between the SCL-SP-ωand iSCL-SPωdecoders is mainly related to two key parameters,i.e.,SM(ω′,T(ω′)) andD(ω′).Besides,sinceD(ω′)is given whenω′is fixed,this performance gap is mainly determined bySM(ω′,T(ω′)),which is further affected by the following two parameters,i.e.,the chosen shifting metricMand the maximum number of re-decoding attemptsT(ω′).Therefore,the performance gap between the SCL-SP-ωdecoder and its lower bound can be narrowed by choosing a properly designed shifting metric and conducting a larger maximum number of re-decoding attempts.

Remark 1.The reasons that SM(ω′,T(ω′))is affected by the chosen shifting metric M and the maximum number of re-decoding attempts T(ω′)are twofold.First,M is designed to predict the shifting bit positions,thus it has a direct impact on the decoding accuracy,i.e.,SM(ω′,T(ω′)).Given T(ω′),applying different shifting metrics will lead to different prediction accuracy S*M(ω′,T(ω′))(will be evaluated in Section V-5.1).Second,define sM(ω′,t)as the probability of successful decoding in the t-th re-decoding attemptof the ω′-th step,thenholds.As can be seen,SM(ω′,T(ω′))is a nondecreasing function with respect to T(ω′).Thus,when M is fixed,the value of SM(ω′,T(ω′))can be increased by adopting a larger T(ω′).

3.2 Computational Complexity

It is seen that a number of re-decoding attempts is required in the proposed SCL-SP-ωdecoder and in each re-decoding attempt,the plain SCL decoding is employed together with SP.Since the complexity of the plain SCL decoding is well-studied in the existing literature,it is not explicitly considered in this work.Instead,the two additional factors that may increase the complexity of the SCL-SP-ωdecoder are analyzed,i.e.,shifting metric calculation and the number of redecoding attempts required.In this subsection,we evaluate the decoding complexity of the SCL-SP-ωdecoder in terms of the average list size.Then,accordingly,we present a criterion for the choice of the maximum number of re-decoding attempts in each decoding step,so as to reduce the computational burden.First,the average number of re-decoding attempts in theω′-th step,i.e.,,is given by

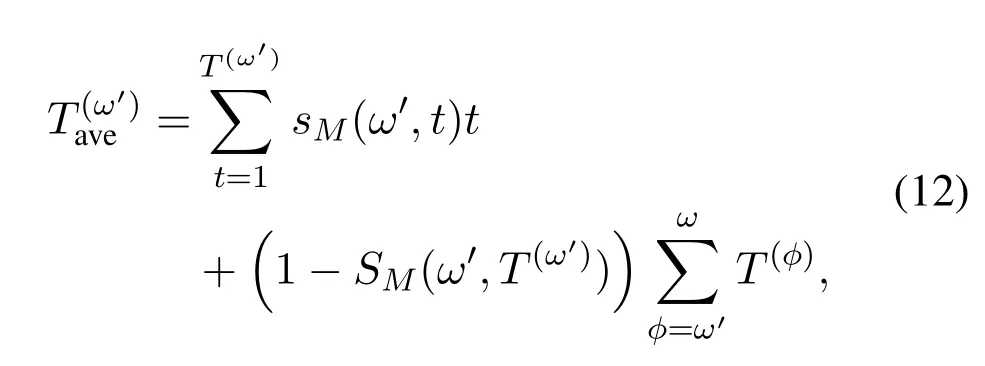
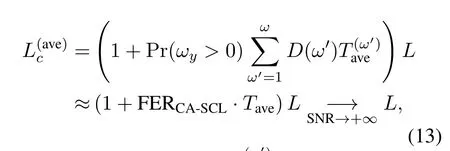
Based on the analysis above,we can see that optimizing the shifting metric is able to improve the error correction performance of the SCL-SP-ωdecoder and in the meantime reduce its decoding complexity.In the next section,we will focus on developing efficient shifting metrics to further improve the SCL-SP-ωdecoder.

IV.PROPOSED SHIFTING METRICS

In order to approach the FER lower bound of the SCLSP-ωdecoder and reduce the number of re-decoding attempts,it is essential to identify whether a bit position has a high probability that the correct path is eliminated.In this section,we first introduce the shifting metrics proposed in [11] and [12],then a simplified shifting metric is derived,which exhibits much lower computational complexity as compared to the existing ones.Moreover,we employ DL techniques to compensate for the performance loss due to the approximations used in the proposed simplified metric.Specifically,a custom-tailored DNN is presented to learn the correlation between the PMs and the shifting positions.Besides,the trainable parameters in the network are treated as perturbation parameters that can be incorporated into the proposed shifting metric to improve its performance.

In[11],the authors proposed an LLR-based metric,which is shown as follows:

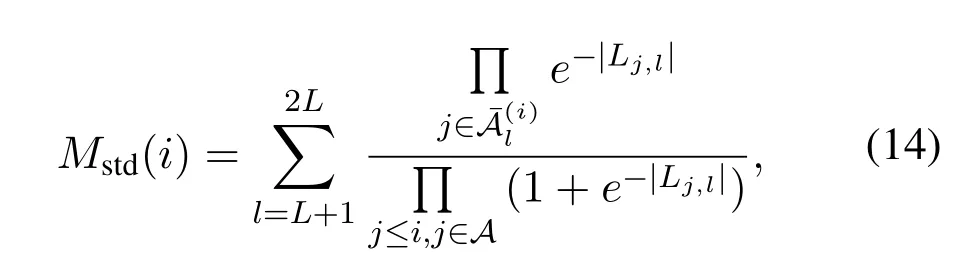
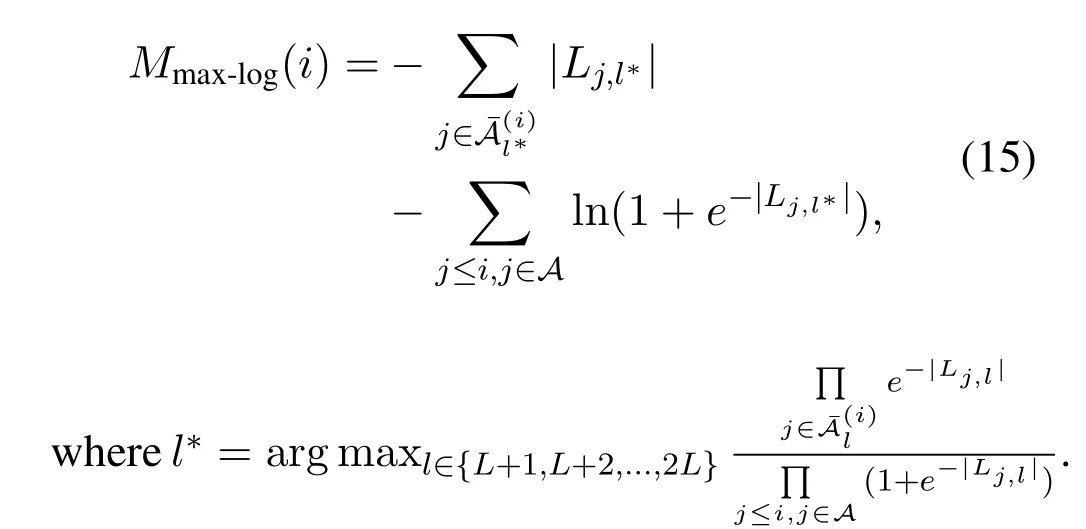
The metrics in Eq.(14) and Eq.(15) both require additional memory space for storing the LLRs of all the bits before the current bitui,thus are not attractive for hardware implementation.To address this issue,the work [12] proposed to use PMs to calculate the reliability of each information bit on-the-fly,and the corresponding shifting metric is given by

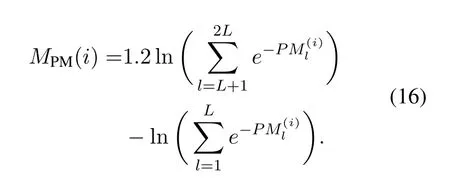
4.1 Proposed Simplified Shifting Metric Based on PM

Efficient hardware implementation of the SCL-SPωdecoder not only depends on the number of redecoding attempts,but also relies on efficient implementation of the shifting metric.However,as can be seen from Eq.(15)and Eq.(16),the calculations of the existing shifting metrics all involve logarithmic and exponential operations that are not hardware-friendly.As a result,designing an efficient shifting metric that only contains addition/subtraction and multiplication operations is an urgent task.In this work,by taking both the reserved and discarded paths into consideration,a new shifting metric(denoted by)is proposed as follows:

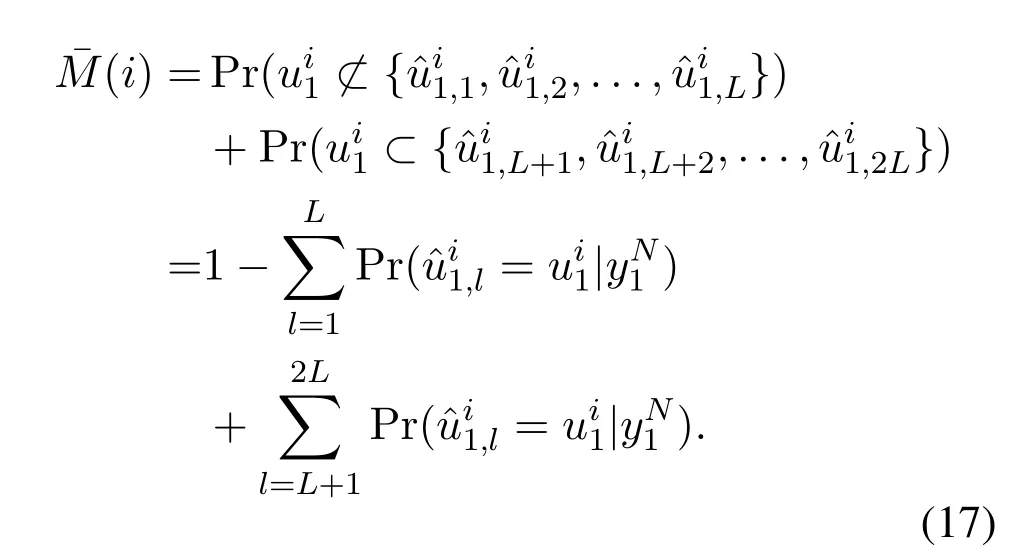
By ignoring the constant term 1 and resorting to the definition of PM,i.e.,we can approximate the metricin Eq.(17)as

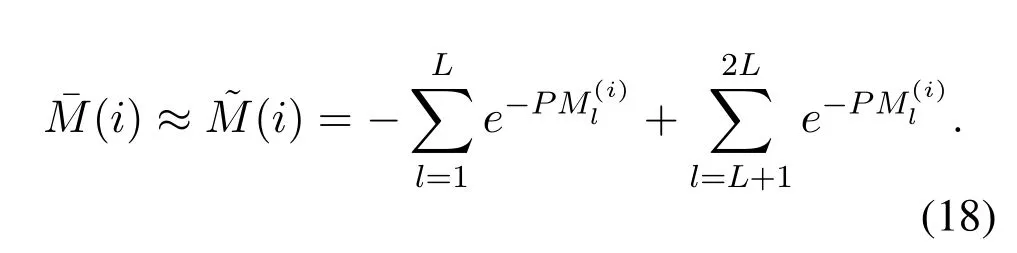
Then,to further reduce the number of exponential operations when calculating,we propose to further approximate the exponential terms in Eq.(18) by using their first-order Taylor expansions.Accordingly,a simplified metricMsim-PMwithout transcendental functions can be derived as

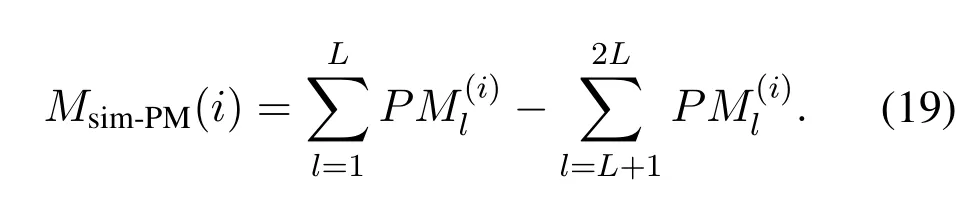
4.2 Improving the Simplified Shifting Metric Using DL

As the approximations utilized above may limit the estimation accuracy of the shifting positions,we introduce a perturbation parameter vectorW=(w1,w2,...,w2L) to improve the performance ofMsim-PM.Specifically,the perturbation parameters are used to refine the PM values in Eq.(19) and accordingly,a new shifting metric is given as follows:

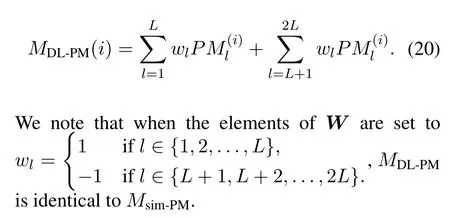
The optimization ofWcan be considered as a learning task,and we employ one of the most popular DL techniques to solve this problem,i.e.,using DNN.Note that the SP scheme is only eligible on the indices that are contained inA*.Therefore,we neglect the unnecessary indices that are not inA*to relieve the learning difficulty.Consequently,MDL-PMcan be represented by the following matrix form:

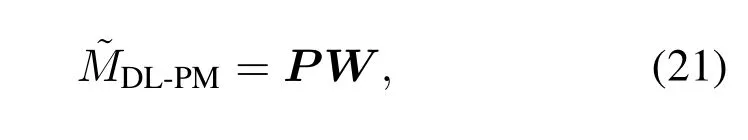
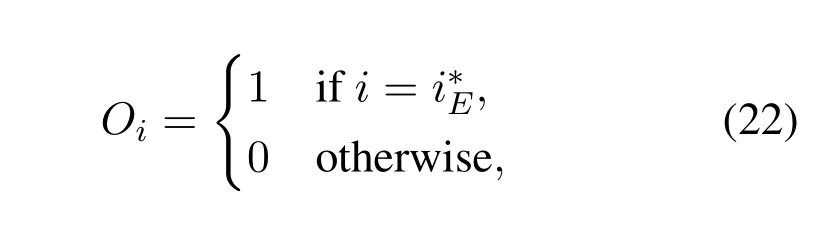
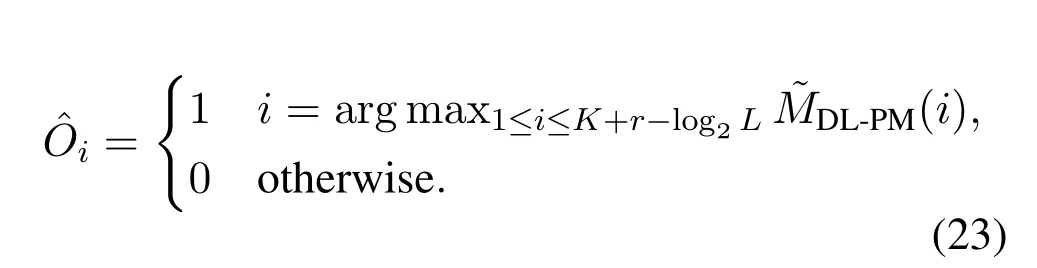
Then the aim of the learning task is to optimize the values ofWvia minimizing the difference between the estimated outputand labelOthrough backpropagation [23].However,the arg max function in Eq.(23) is a non-differentiable discrete function,which hinders the gradients from propagation during network training.As a result,we utilize the differentiable softmax function to approximate the arg max function and thencan be approximated by

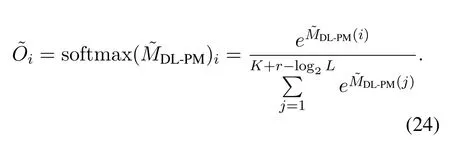
Figure 3 shows the structure of the proposed DNN,forP(16,9,0) withL=8.As can been observed,there are three layers,i.e.,the input layer,the fullyconnected(FC)layer,and the output layer.The input of the network is the PM matrixP,thus the input layer contains(K+r-log2L)×2Lneurons.In our network,the neurons in each row ofPshare the same weightWand there is no bias term.The number of neurons in the FC layer isK+r-log2Land no activation function is applied.The output layer also hasK+r-log2Lneurons and each neuron represents one information bit inA*.For example,as shown in Figure 3,the second neutron of the output layer marked with green corresponds to the bitu12in the given code tree.

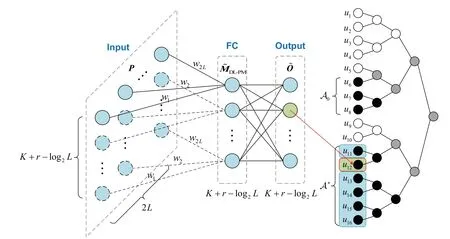
Figure 3. The structure of the proposed DNN,for P(16,9,0)with L=8.

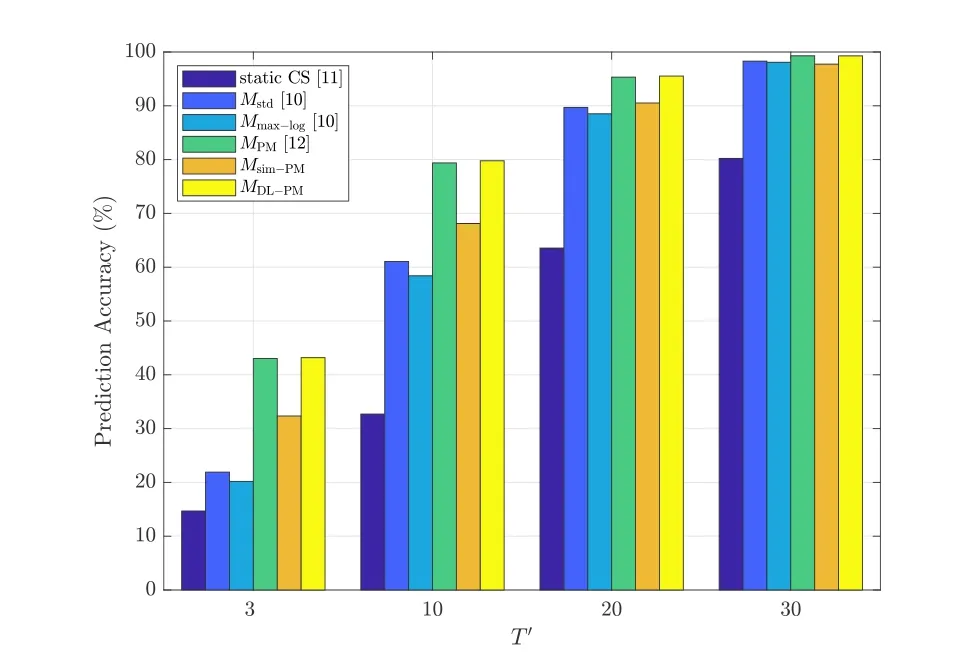
Figure 4. Prediction accuracy of various shifting metrics.

Finally,the network is trained by minimizing the following binary cross-entropy loss betweenOand:

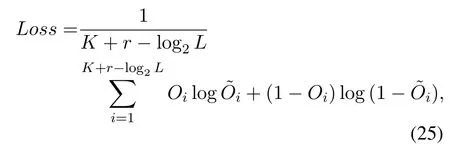
and the adaptive moment estimation (Adam) optimizer[24]is used.To accelerate the training process,Wis initialized as[11×L,-11×L]Tto guarantee thatMDL-PMcan achieve the same prediction performance asMsim-PMat the beginning of training.Besides,we emphasize that in this work the perturbation parameters inWcan be directly used to calculate Eq.(20)and determine the shifting positions after offline training,instead of conducting one forward-propagation of the whole network as in work [21].This can relieve the computational burden caused by the calculation and storage of intermediate variables in order from the input layer to the output layer.However,the optimalWmay differ when different orders of noise realizations are considered.For simplicity,we only optimizeMDL-PMforω=1 in the following,and the correspondingWis applied in the other cases with different values ofω.

Remark 2.The proposed DNN model is closely related with the two successful decoding conditions mentioned in Section III-3.1.This is because the iSCL-SP-1 decoder is employed to collect the training labels,thus the correct Ey is always contained inand there is no CRC collision during the decoding.

V.SIMULATION RESULTS

In this section,we evaluate the performance of the SCL-SP-ωdecoder with the proposed shifting metrics and compare it with the CA-SCL and SCL-SP decoders.The simulation setup is summarized in Table 4.Unless otherwise specified,the list sizeLand offsetkare both set to 8 in our simulations.Throughout this section,the polar code concatenated with 8-bit CRC,i.e.,P(256,128,8),is considered,where all the binary message bits are randomly produced and the CRC generator polynomial isx8+x7+x6+x5+x4+x3+1.The information and frozen sets,i.e.,AandAc,are constructed based on Gaussian approximation [25] atEb/N0=2.0 dB.All the simulations are conducted with MATLAB R2018b.Our training model is developed with a Python 3.6 IDE using the advanced deep learning framework TensorFlow 1.13.1[26].We utilize the cross-validation method to choose the best group of hyperparameters,which are set as follows.The training data set is constructed by collecting 104samples of received signal vectors,which are not correctly decoded by the iSCL-SP-0 decoder,atEb/N0=2 dB.In the training phase,the number of training epochs,batch size and learning rate are setto 50,200 and 10-3,respectively.All experiments are conducted on the Intel i5-9400 CPU@2.9 GHz,16G RAM and NVIDIA GeForce GTX 2080 Ti GPU.

Table 4. Simulation setup.

Table 5. Computational complexity analysis of different shifting metrics.

5.1 Evaluation of the Shifting Metrics

The probability of successful decodingSM(ω′,T′) is affected not by the following factors: the chosen metricM,the value ofT′and the reliability of CRC.In order to verify the effectiveness of various shifting metrics,we focus on the probability that the noise realizations of orderω′can be corrected by the SCL-SP-ωdecoder withinT′re-decoding attempts,which is denoted by(ω′,T′).In particular,(1,T′)also denotes the prediction accuracy of a chosen metric (or the static CS)in the iSCL-SP-1 decoder for simplicity,and it can be regarded as the frequency thatiEis in

Figure 4 presents the prediction accuracy achieved by various shifting metrics with different values ofT′atEb/N0=2.0 dB,whereT′={3,10,20,30}.As can be observed,the prediction accuracy of the static CS is much lower than those of the other shifting metrics,since the static CS does not take the er-ror distribution characteristics in SCL decoding into consideration.Besides,the metricsMstdandMmax-log(given in Eq.(14)and Eq.(15),respectively)have similar prediction accuracy and are both outperformed by our proposed simplified metricMsim-PMin Eq.(19)and DL-aided metricMDL-PMin Eq.(20).Among all the shifting metrics,the proposed DL-aided metricMDL-PMachieves the highest prediction accuracy.Moreover,it is also worth mentioning that the prediction accuracy achieved byMDL-PMwithT′=10(79.78%) is comparable to that by the static CS withT′=30 (80.22%),which shows that by employing an efficient metric the number of re-decoding attempts can be significantly reduced.

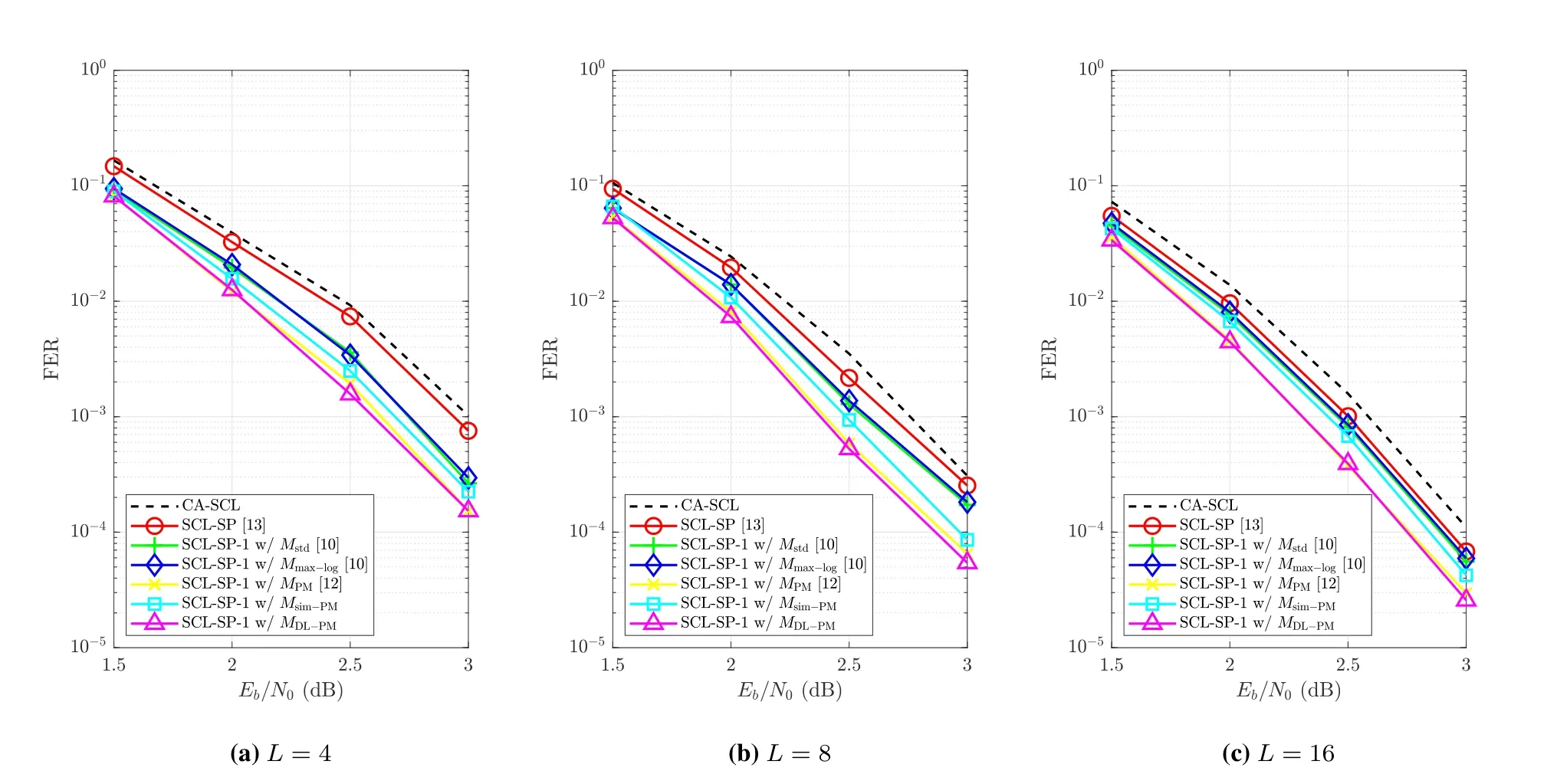
Figure 5. FER performance of the SCL-SP-1 decoder when using different metrics.

Then,we evaluate the computational complexity of the considered shifting metrics,which is shown in Table 5.It is observed that the computational costs of employingMstdandMmax-log,in terms of the number of exponential/logarithmic calculations during one decoding attempt,both increase withLandK.Moreover,these two shifting metrics require additional memory space to store the LLRs of the information bits.On the contrary,since only the PM values at the current information bit is required forMPM,Msim-PMandMDL-PM,the memory cost is significantly reduced as compared toMstdandMmax-log.However,MPMstill suffers from high computational complexity as transcendental functions are required to be calculated at each information bit.Overall,our proposed shifting metrics,i.e.,Msim-PMandMDL-PM,exhibit much lower computational complexity,and consequently are more suitable for hardware implementation.

5.2 Evaluation of the SCL-SP-ω Decoder

In Figure 5,we compare the FER performance of the CA-SCL,SCL-SP [13],and SCL-SP-1 decoders forL=4,8,16,where the maximum number of redecoding attempts for the SCL-SP and SCL-SP-1 decoders are both set to 10.It can be seen that the SCLSP-1 decoder outperforms the CA-SCL decoder and the corresponding performance gain ranges from 0.3 dB to 0.4 dB at FER=10-3.Moreover,one can observe that the shifting metric that provides a higher prediction accuracy imposes a lower FER.In particular,the performance of the SCL-SP decoder is inferior to that of the SCL-SP-1 decoder,since the static CS yields the worst prediction accuracy as compared to the other shifting metrics(as shown in Figure 4).Besides,althoughMsim-PMincurs a slight degradation on FER performance as compared toMPM,it still outperforms the two LLR-based shifting metrics,i.e.,MstdandMmax-log.Among all the shifting metrics,MDL-PMachieves the best performance for all values ofLevaluated.However,the performance gap between the SCL-SP-1 decoder and the CA-SCL decoder gradually narrows asLgrows.This is becauseD(1) decreases asLbecomes larger,and hence the upper bound of the performance gain,i.e.,will diminish asLincreases.

Next,we illustrate the complexity of different decoders,in terms of the average list sizeTave,which is shown in Figure 6.As can be seen,for the SCLSP-1 and SCL-SP decoders,their average list sizes gradually approach the list size of the CA-SCL decoder in the medium-to-high SNR regime.The performance of the CA-SCL decoder with a larger list size (e.g.,L=8 orL=16) is comparable to the SCL-SP-1 decoder with a smaller list size(e.g.,L=4 orL=8).Specially,the SCL-SP-1 decoder withMDL-PMandL=4 is similar to the CA-SCL decoder withL=16,in terms of both FER performance and average list size.Therefore,the SCL-SP-1 decoder with a proper shifting metric can achieve a considerable performance gain over the CA-SCL decoder,especially in the medium-to-high SNR regime.

In Figure 7,we compare the FER performance of the CA-SCL,SCL-SP and SCL-SP-ω(ω=1,2) decoders,for different values ofT.For the SCL-SP-2 decoder,we consider two different configurations ofT(ω′),i.e.,T(1)=T(2,1)=40,T(2,2)=10 andT(1)=T(2,1)=20,T(2,2)=21.Note that the maximum numbers of re-decoding attempts under these two configurations are the same.As can be observed,the performance of the SCL-SP decoder is far from the FER lower bound despite that the whole search space of the static CS is traversed,i.e.,T=|Sstatic|=34.On the contrary,the performance of the SCL-SP-1 decoder with the proposedMDL-PM(withT(1)=40)can closely approach the theoretical FER lower bound provided by the iSCL-SP-1 decoder.However,different from the SCL-SP-1 decoder,the performance achieved by the SCL-SP-2 decoder is unable to approach the corresponding theoretical FER lower bound.This is mainly due to the following two reasons: 1)T(2)is much smaller than the size of the searching space whenω=2 (i.e.,T(2)≪),and 2) the probability that the CRC is verified by one of the previous decoding outputs before the true one increases with the number of re-decoding attempts,and this leads to a non-negligible performance loss.Besides,we also provide the comparison betweenMPMand the proposed DL-aided metricMDL-PM.It can be seen that the performance of the SCL-SP-2 decoder usingMDL-PMis similar to that usingMPMwhen all the other parameters are the same,which shows that with the aid of DL our proposed shifting metric can achieve much lower computational complexity yet with almost no performance loss.

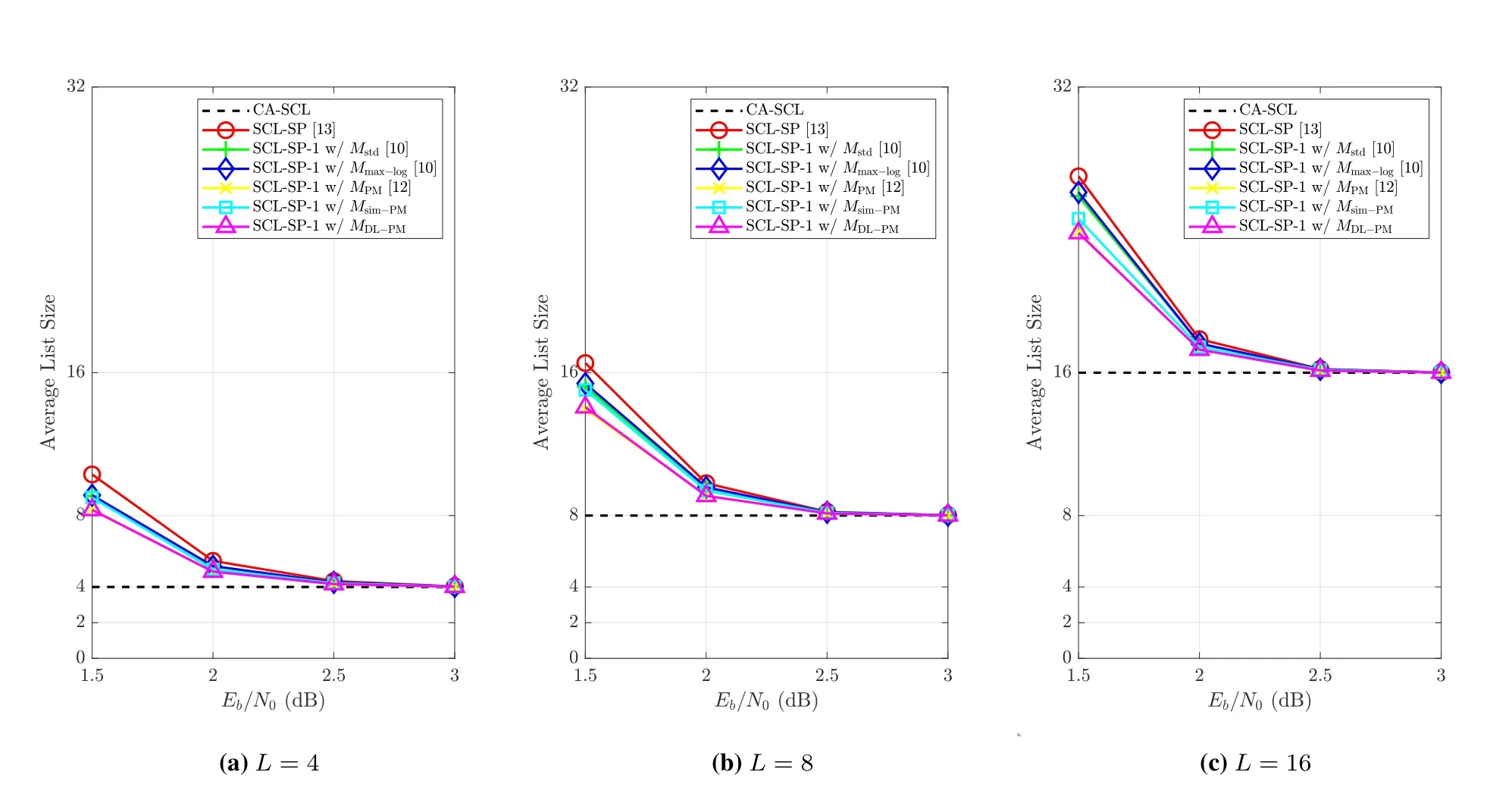
Figure 6. Average list size of the SCL-SP-1 decoder when using different metrics.

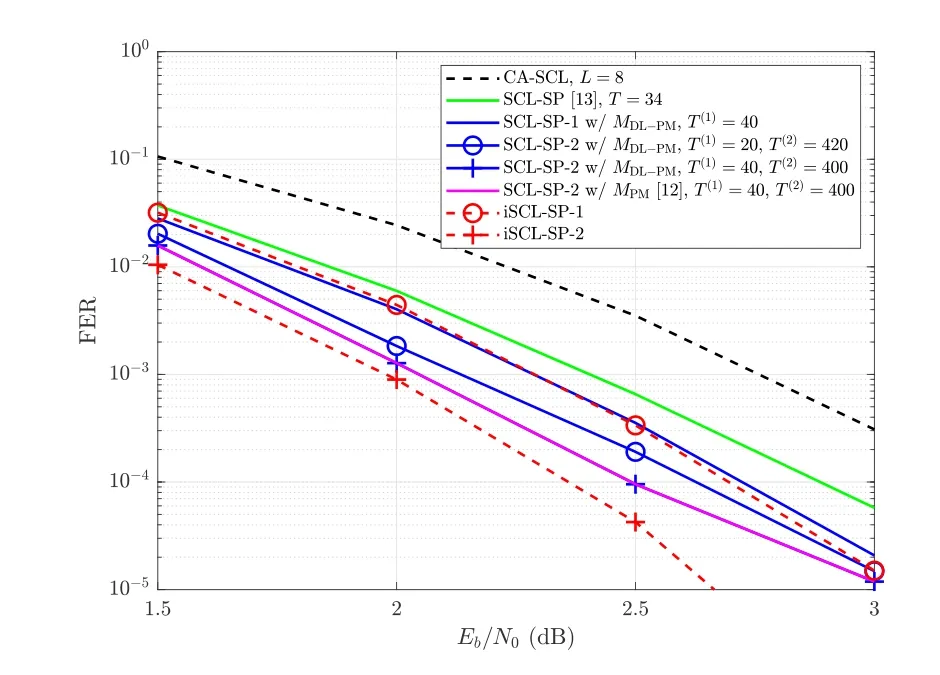
Figure 7. FER performance comparison of the CA-SCL,iSCL and SCL-SP-ω(ω=1,2)decoders.

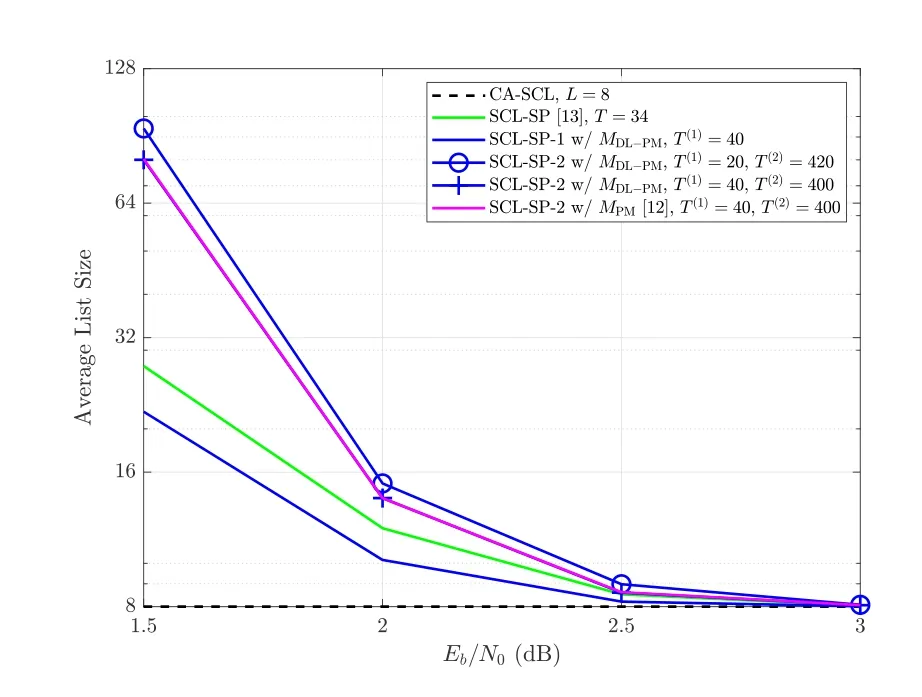
Figure 8. Complexity comparison of the CA-SCL,iSCL and SCL-SP-ω(ω=1,2)decoders.

Finally,in Figure 8,we compare the complexity of the considered decoders using the same simulation parameters as those in Figure 7.It can be observed that employingMDL-PMnot only permits a better error correction performance but also reduces the average list size by 21.1%,as compared to using the static CS.In addition,it can be observed that the SCL-SP-2 decoder withT(1)=40,T(2)=400 exhibits a slight FER gain(0.1 dB)over that withT(1),T(2)=420,yet with reduced average list size(about 14.9%atEb/N0=1.5 dB).This suggests that increasingT(1)for the SCLSP-2 decoder is beneficial for reducing the decoding complexity.

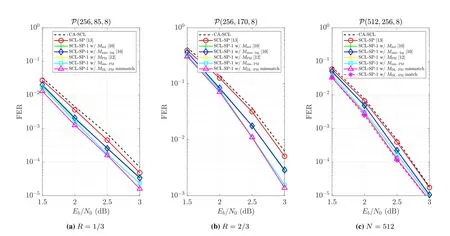
Figure 9. FER performance of the SCL-SP-1 decoder with different code parameter.

5.3 Evaluation of the Proposed DL Model

In Figure 9,we compare the FER performance of the SCL-SP-1 decoder when using different code parameters,where the legend“match”indicates that the code parameters used during the training of the perturbation parameterWmatches with those during performance evaluation,while“mismatch”means the opposite.and“match”indicate that the perturbation parametersWused inMDL-PMare obtained according toP(256,128,8) or according to the matched code parameter,respectively.As can be seen in Figure 9(a)and Figure 9(b),the performance achieved byMDL-PMis similar to that byMPMwhen the code rateR=K/Nchanges.This is because the DNN structure does not change given fixedN,which means that the proposed DL model is robust to the change ofR.From Figure 9(c),it is observed that although the proposed learning-based model is designed forP(256,128,8),the obtained perturbation parameterWcan still be applied toP(512,256,8) without much performance degradation.Therefore,although DNN is used for our proposed shifting metric,re-training is generally not required whenNorRchanges.Besides,the number of trainable parameters is only 2L.This implies that the proposed DL model is lightweight as compared with other popular model-driven networks,such as CNN,LSTM,etc.,which usually contain thousands of training parameters.Therefore,the proposed DL model is low-complexity and robust to the change of code parameters.

VI.CONCLUSION

In this paper,we studied the SCL-SP-ωdecoder,and analyzed its theoretical FER performance lower bound and decoding complexity.The analysis unveils that the performance and complexity of the SCL-SP-w decoder are closely related with the bit shifting metric employed.We then presented a simplified shifting metric derived from the PM domain,and designed a custom-tailored DL network to further improve it.The proposed shifting metrics are both free of transcendental functions.Simulation results showed that adopting the proposed metrics incurs almost no performance loss,yet with much lower computational complexity.

ACKNOWLEDGEMENT

This work was supported in part by the National Key Research and Development Program of China under Grant 2018YFB1802303,and in part by the Zhejiang Provincial Natural Science Foundation of China under Grant LQ20F010010.

NOTES

1Besides the CRC codes,the performance of the SCLSP-ωdecoder may be further enhanced by it with the parity-check codes [27,28],which is left for future work.

2Note thatis generated only based on the initial standard SCL decoding.

3Note that Algorithm 1 will reduce to the SCL-SP-1 decoder if it stops at line 20.

4Note that the iSCL-SP-0 decoder is equivalent to the standard SCL decoder attached with a perfect CRC detector.