Learning-Based Joint Service Caching and Load Balancing for MEC Blockchain Networks

Wenqian Zhang,Wenya Fan,Guanglin Zhang,*,Shiwen Mao

1 College of Information Science and Technology,Donghua University,Shanghai 201620,China

2 Engineering Research Center of Digitized Textile and Apparel Technology,Ministry of Education,Shanghai 201620,China

3 Department of Electrical and Computer Engineering,Auburn University,Auburn,AL 36849-5201,USA

Abstract: Integrating the blockchain technology into mobile-edge computing (MEC) networks with multiple cooperative MEC servers (MECS) providing a promising solution to improving resource utilization,and helping establish a secure reward mechanism that can facilitate load balancing among MECS.In addition,intelligent management of service caching and load balancing can improve the network utility in MEC blockchain networks with multiple types of workloads.In this paper,we investigate a learningbased joint service caching and load balancing policy for optimizing the communication and computation resources allocation,so as to improve the resource utilization of MEC blockchain networks.We formulate the problem as a challenging long-term network revenue maximization Markov decision process(MDP) problem.To address the highly dynamic and high dimension of system states,we design a joint service caching and load balancing algorithm based on the double-dueling Deep Q network(DQN)approach.The simulation results validate the feasibility and superior performance of our proposed algorithm over several baseline schemes.

Keywords: cooperative mobile-edge computing;blockchain;workload offloading;service caching;load balancing;deep reinforcement learning(DRL)

I.INTRODUCTION

Mobile edge computing (MEC),deployed in proximity to mobile devices (MD),is a promising technology to deal with latency-critical and computingintensive workloads in the prospective Internet of Things (IoT) [1].Establishing trust among multiple parties (e.g.,edge/cloud providers) in MEC networks utilizing multiple servers (MECS) is a challenge because these parties often have conflicts of interest [2].Blockchain,as an emerging decentralized security system [3,4] and a public ledger of various types of transactions [5],has been incorporated in numerous applications,e.g.,bitcoin,IoT,and smart grid,etc.[6].Integrating the blockchain technology,with their advantages of decentralization,trust,and anonymity,into MEC systems has attracted great interest [7].Compared with the traditional cooperative MEC system with a single central authority,the MEC system empowered by blockchain can enable decentralized,secure communications among cooperative MECS [8].Because the MECS have the reputation records in the MEC Blockchain network,which motivates the MECS to process more workloads while meeting the requirements of MDs.This promotes load balancing among multiple MECS and full utilization of network computing resources.

In order to satisfy the service requests for delaysensitive workloads and achieve high utilization of resources in MEC blockchain networks,edge caching[9,10]and load balancing among cooperative MECS[11]were proposed.Edge caching can prestore the necessary application data at MECS for computing service,which can reduce the backhaul transmission delay to the core network and better utilize the service capability of MECS [12,13].In addition,MEC blockchain networks usually carry highly dynamic,diverse,and computation intensive workloads,which are difficult for a single MEC server to process [14].Load balancing can reshape the workload distribution in MEC blockchain networks and facilitate the appropriate use of their limited computing resources[11].In addition,the cooperative MEC networks empowered by blockchain can establish a secure reward mechanism to facilitate load balancing among MECS.

Most existing works are focused on secure workload offloading schedules [15,16],credible data transmission schemes [17],the cooperation among MECS [18],and allocation of the limited communication and computation resources [19-21] in MEC blockchain networks,which attempted to improve the service capabilities or maximize the long-term system profits.Due to the complex process of solving these problems,it usually takes a long time for the iterative procedure to converge to the optimal solution [22].In addition,the basis for the blockchain mechanism is a computing process called mining.Nevertheless,the mining process (e.g.,performing Delegated Proof of Stake(DPoS))[23]and workload computing in MEC systems are generally complicated and require considerable storage and computing resources[24].Therefore,developing an intelligent and self-organizing resource allocation scheme is critical in MEC blockchain networks with limited service capabilities.To this end,deep reinforcement learning(DRL)was introduced to obtain optimal strategies and maximize long-term rewards [25,26].In [27],the DRL was introduced to optimize the energy allocation and minimize the system cost under highly dynamic and high-dimensional system states.The recent work in [28] performed task scheduling to maximize the long-term mining reward with the minimum cost on resources by leveraging DRL.

In this paper,we investigate the problem of joint service caching and load balancing for blockchainauthorized MEC networks with multiple cooperative MECS and multiple types of workloads.We aim to establish a secure load balancing mechanism to maximize the utilization of service resources in the MECS,and to jointly optimize service caching,workloads offloading,and service resources allocation strategies to achieve a high network revenue as well as meet the workload requirements.In particular,we present the main contributions of this work as follows.Firstly,we consider an MEC blockchain network with multiple cooperative MECS and MDs,as well as multiple types of workloads.We establish a secure load balancing mechanism based on blockchain to improve the service capability,and maximize the utilization of service resources of the network by optimizing the allocation of communication and computation resources.Secondly,we formulate the long-term network revenue maximization in MEC blockchain networks as an MDP problem.We then design a double-dueling DQN based joint service caching and load balancing algorithm to solve the formulated problem,which is characterized by the highly dynamic and high dimensional system states.Lastly,we analyze the convergence and performance of the proposed scheme through extensive simulations.Compared with several benchmark algorithms,the proposed algorithm achieves a greater network revenue while better satisfying the requirements of workloads.

The remainder of this work is organized as follows.In Sections II and III,we introduce the system model and problem formulation,respectively.In Section IV,we present the double-dueling DQN based joint service caching and load balancing algorithm.In Section V,we discuss the simulation results and performance analysis.We conclude the paper in Section VI.

II.SYSTEM MODEL

2.1 MEC Blockchain Networks

As depicted in Figure 1,we propose a blockchainenabled mobile edge computing network with multiple cooperative MECS and MDs,which consists of an MEC system and a blockchain system.We consider that the MEC blockchain network hasMMEC servers denoted by a setM≜{1,2,...,M},andNMDs denoted by a setN≜{1,2,...,N}.The data traffic between MDs and MECS is transmitted through wireless channels,and its transmission mechanism is based on Orthogonal Frequency-Division Multiple Access(OFDMA)[29].The cooperative MECS communicate over a wireline Local Area Network(LAN).

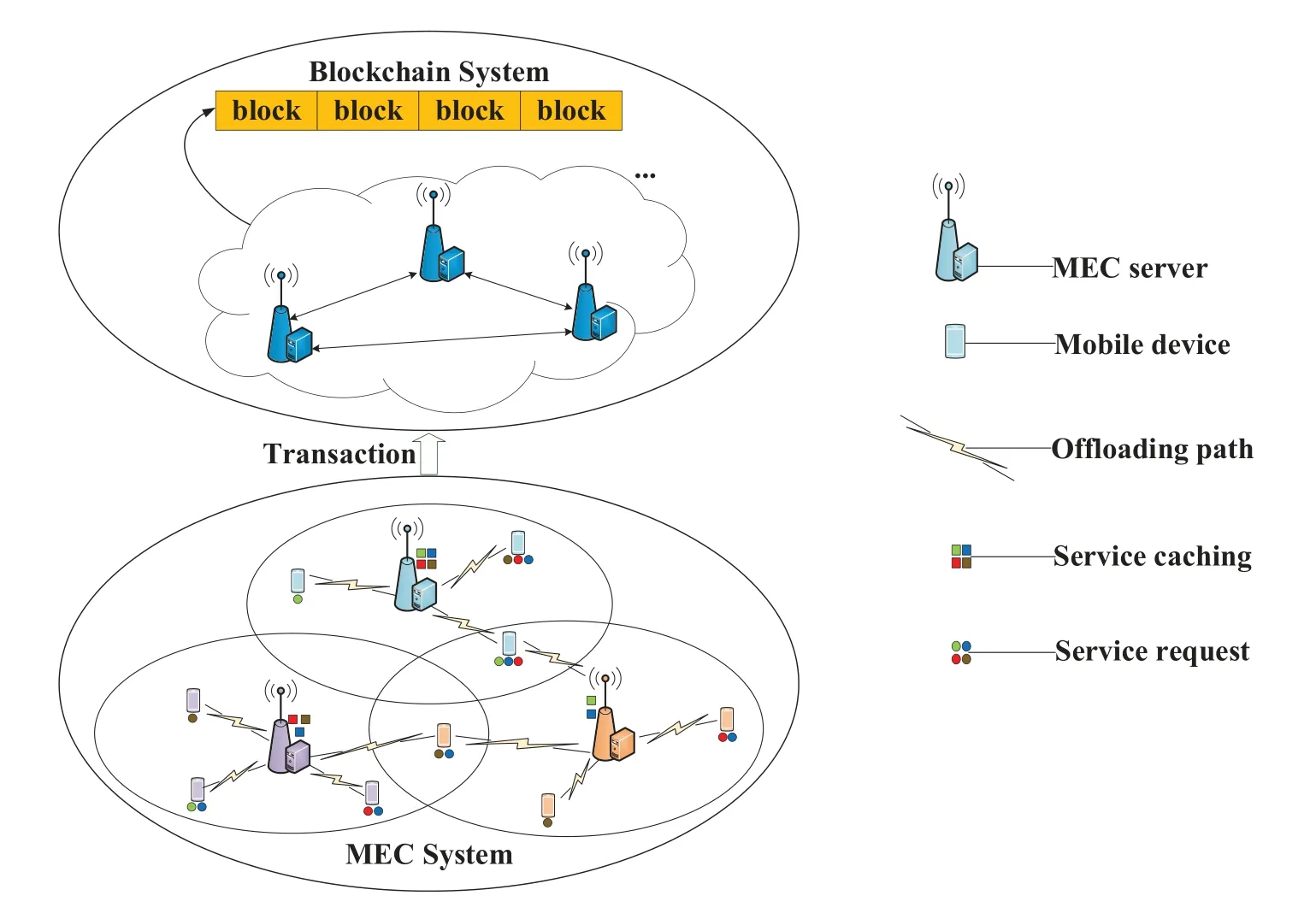
Figure 1. Architecture of the MEC blockchain network considered in this paper.

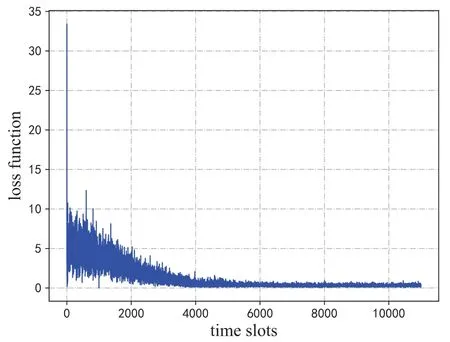
Figure 2. Convergence performance of the proposed algorithm as indicated by the evolution of the loss function.

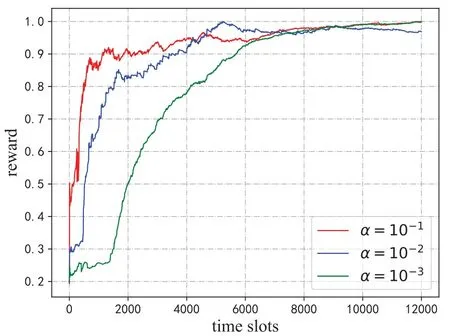
Figure 3. Reward function value vs.different learning rates.

In the MEC system,we denoteNm ⊆Nas the subset of MDs associated with MEC serverm(e.g.,MDnis the subscribe of the MEC serverm,which is termed the“associated relationship”between MDnand MEC servermin this paper),and the MEC servermprovides computation services for the MDs inNmto obtain payoffs from the system.We assume that the MDs in the overlapping coverage area of multiple MECS can transmit workloads directly to the corresponding MEC server.After the computation results are returned,each MD will provide the corresponding MEC server a service evaluation score,which is related to the reputation value of the MEC server.

To ensure the security and privacy of the MEC system,we introduce the blockchain technology into the MEC network.The blockchain system can collect and store information from the MEC system,such as workload offloading records and the MEC server’s reputation value.Such information will be grouped into data blocks and recorded on the blockchain after consensus is reached (e.g.,the Nakamoto consensus agreement).TheMMEC servers act as miners in the blockchain system,where the first miner to solve the consensus problem will obtain the mining reward and broadcast the verified transaction to other blockchain nodes in a safe and immutable manner[6].

2.2 Workload Arrival and System Service Capability

The proposed system operates over discrete time periodsT≜{0,1,...,T}.In each time slott,the workloads generated by each MD will be offloaded to one of the associated MEC server for execution.For the MDn,the types of generated workloads in time slottcan be modeled as a setK={1,2,...,K}.Without loss of generality,we assume that the workloads from MDnarrive at MECmfollow a Poisson distribution with rateπn,m(t) in time slott[30].We denoteas the proportion of typekworkloads to the total workloads generated by MDn,andis the set of workload percentages.The execution requirements for the typekworkloads generated by MDnassociated with MEC servermare modeled as a vector of four tuples,which is denoted by.For the typekworkloads,ak(in GB)indicates the required storage capacity,dk(in Mb/workload)is the data size of each workload,hk(in CPU cycles/Mb)denotes the required CPU cycles for workloads execution,andτk(in sec)is the maximum execution delay deadline.

We consider the case that the MECS have limited service capabilities(e.g.,computation capability,storage capacity,and communication capability),and the MEC with a heavier loads can transfer some workloads to the MECS that have lighter loads to achieve load balancing through the LAN.We denoteRmandFmas the overall storage capacity and computation capability of MEC serverm,respectively.Since the different execution requirements of each type of workloads,only the MECS that have cached the related applications data are eligible to provide services for the corresponding types of workloads.

2.3 Service Caching and Load Balancing

MDnsends service requests to the connected MECS at each time slott.The service requests from MDnfor typekworkloads can be processed only when MECmhas cached the corresponding application data and has sufficient service resources.Letxm(t)={xkm(t)∈{0,1}|m ∈M,k ∈K}be the set of service caching decisions of MEC servermat time slott,which is used to indicate whether the application data for typekworkloads is cached at MEC serverm(whenxkm(t)=1) or not (whenxkm(t)=0) at time slott.Note that the service caching decisions are constrained by the overall storage capacity of MEC serverm,i.e.,

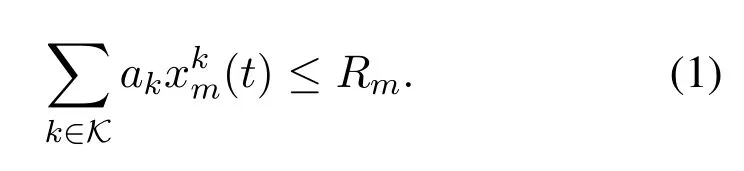
When the service requests of MDs inNmarrive at the associated MEC servermat each time slot,the load balancing among the cooperative MECS will be implemented by transmitting the redundant workloads to nearby MECS with low loads.Denotezm(t)=as the set of load balancing decisions among MECS for MEC servermat time slott,whereis the proportion of thek-type of workloads transmitted from MEC servermto MEC serverl.

LetNml ⊆ Nmbe the set of MDs associated with MEC servermin the overlapping area of MEC servermand MEC serverl.Note that,whereNmmindicates the set of MDs associated with MEC servermonly within the coverage area of MEC serverm.We denote,k ∈K}as the workload offloading decisions for MDnassociated with MEC serverm,wheremeans that the workloads generated by MDnare offloaded to MEC servermat time slott.Similarly,indicates that the workloads are transmitted to MEC serverlfrom MDnassociated with MEC servermdirectly.Note that if and only ifn ∈Nml,we have,otherwise.In addition,the workloads can only be processed on the MEC servermthat caches the application data for typekworkloads.Thus we have

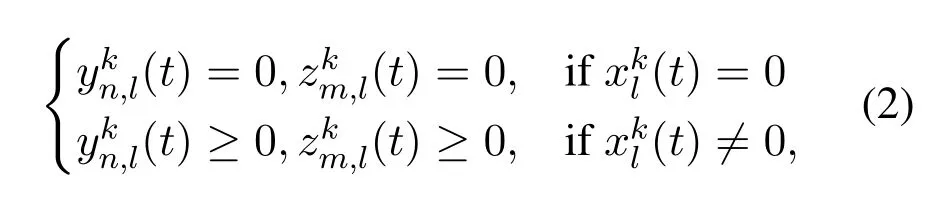
where(t)∈{0,1}|l ∈M,k ∈K}is the service caching decision of MEC serverlat time slott.

2.4 System Cost

In the cooperative MEC system,we mainly consider the cost related to energy consumption and execution delay,which is determined by the following processes:(i) workload offloading to MECS;(ii) load balancing among MECS;and(iii)workload execution at MECS.

2.4.1 Workload Offloading to MECS

In view of the OFDMA transmission mechanism,interference between multiple MDs is ignored due to different MDs occupy non-overlapping subcarrier sets.We assume that there are|S|subcarriers available for data wireless transmission among MEC servermand multiple MDs in its service area,which is denoted byS={1,2,...,s,...|S|}[29].Andwn,m(t)is the bandwidth of one of the subcarrier for the uplink data transmissions from MDnto MEC serverm.The sum of occupied bandwidth resource of all MDs in the coverage area of MEC servermcan not exceed the whole bandwidth resource of MEC serverm,i.e.,

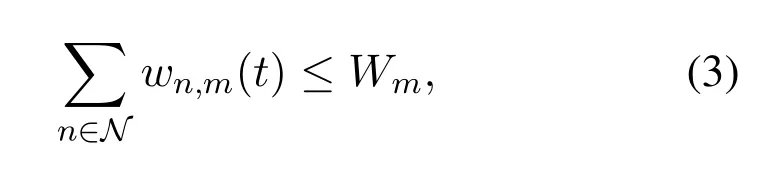
whereWmis the overall available bandwidth resource of MEC serverm.

In each time slott,the workloads generated by the MDs associated with MEC servermcan be offloaded to MEC servermfor execution,and then the processing results will be returned to MDs.Without loss of generality,we focus on the energy consumption of the uplink data transmission and execution delay.According to Shannon’s theorem,the uplink data transmission rate between MDnand MEC servermis given by

2.4.2 Load Balancing Among MECS

Recall that the data transmission among MECS is through a wireline LAN with limited capacity,which incurs congestion delay.According to[30],the service capacity of the LAN is denoted as 1/η,which follows the negative exponentially distribution.The data transmission among MECS for load balancing is modeled as an M/M/1 queuing system [31],which can be described as:

wherePm,g(t)is the energy consumption per unit time for data transmission.Therefore,we obtain the overall system cost of MEC servermfor load balancing among MECS at time slott,which can be written as:

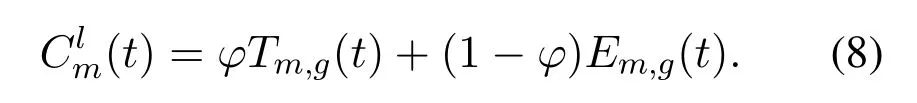
2.4.3 Workload Execution at MECS

The total amount of workloads of the typekcomputed by MEC servermat time slottis denoted as(t),and it follows the Poisson process with rate(t),which can be described as:

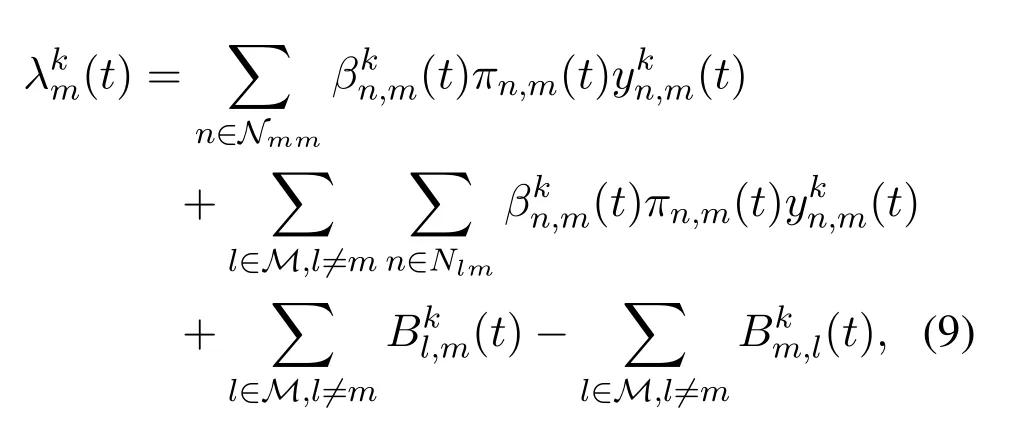
where the first term is for the workloads offloaded from MDs inNmmto MEC servermat time slott.The second term indicates the workloads transmitted by MDs in the overlapping areas between MEC servermand the other MECS,in which{Nlm}l∈M,lmis the set of MDs associated with MEC serverlin the overlapping areas of MEC serverland MEC serverm,andmeans that the workloads are transmitted to MEC servermfrom MDnassociated with MEC serverldirectly.The third and fourth items are the workloads transmitted by other MECS to MEC servermand the workloads transmitted by MEC servermto the other MECS,respectively.

According to the M/M/1 queuing model [31] and Little’s law[32],we obtain the average execution delay for typekworkloads at MEC servermas follows:

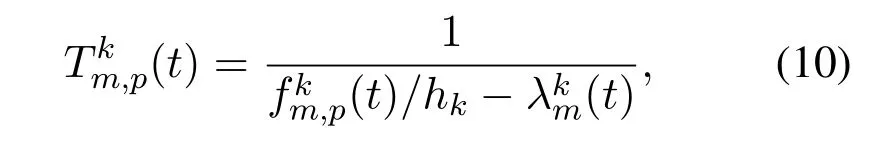
where(t)is the allocated computation capability of MEC servermfor thek-type workloads at time slott.(t)/hkis the service capacity of MEC servermfor workloads execution related to typekworkloads,which follows a negative exponential distribution[30].We obtain the average energy consumption computed by MEC servermfor typekworkloads in time slottas:

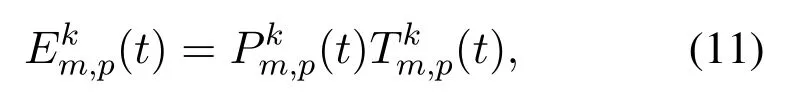
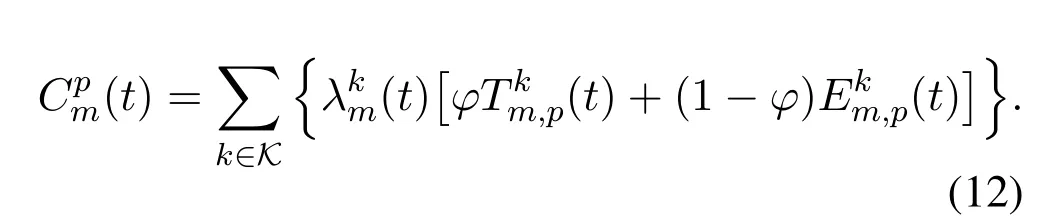
Therefore,the total cost of MEC servermin the cooperative MEC system at time slottcan be written as

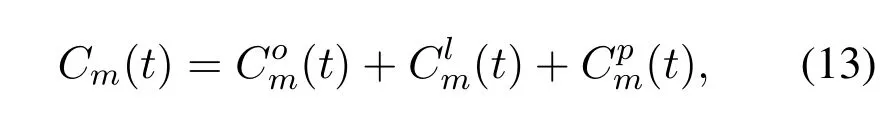
the total system cost is closely related to the MEC’s service caching decisions,workload offloading decisions,and load balancing decisions.

2.5 System Reward

In the MEC blockchain network,the MECS can be rewarded in the following two ways: (i) providing workload processing services for MDs;(ii) being the first miner to solve the consensus problem.We next present the models for the workload execution payoffs and mining payoffs in detail.

2.5.1 Payoffs for Workload Execution

In order to incentivize load balancing among MECS,we introduce the payoffs for workloads execution.The payoff is related to not only the data size of the workloads,but also the reputation of each MEC server.Letbe the service evaluation results given by MDnfor processing typekworkloads at MEC servermin time slott.Thenis the set of service evaluation results of MDs for MEC servermfor processing all types of workloads.

where the first term is the credibility evaluation results of MEC servermby MDs inNmm,the second term means that the credibility evaluation results of MEC servermby MDs in the overlapping areas between MEC servermand the other MECS,ξis the weight coefficient,andn1andn2are the corresponding number of MDs.

According to the data size computed by MEC servermand the reputation of MEC servermat time slott,we obtain the payoff of MEC servermfor processing typekworkloads at time slottas

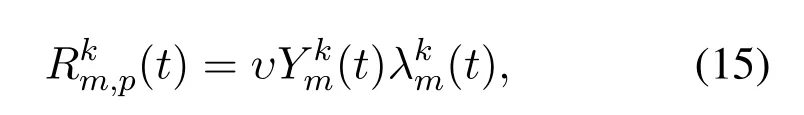
whereυis the unit system payoff of MEC servermfor executing typekworkloads.

In summary,the MEC sever with higher reputations and processed more workloads will obtain more payoffs.Thus,the network is more inclined to load balancing among multiple MECS for maximizing the utilization of computation resources to process more workloads,and each MEC server will also pay more attention to its own reputation (which is related to quality of service).Therefore,the MEC system empowered by blockchain help us establish a more decentralized and secure cooperative MECS network.

2.5.2 Mining Payoffs

In the proposed system,MEC servermalso acts as a miner to process the mining service to obtain the mining payoffs in each time slott.Letfm,b(t) be the allocated computation capability by MEC servermfor mining service at time slott.The ratio offm,b(t)over the sum of the computing capability allocated to mining services by other MECS can be expressed as

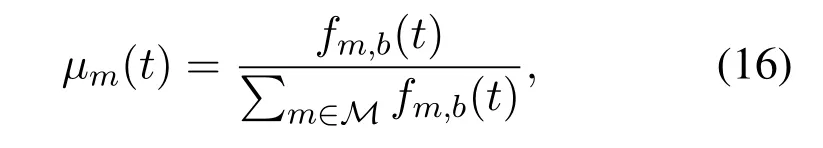
which is directly proportional to the success of mining competition and satisfiesIn addition,in the propagation stage for mined block of MEC servermin the blockchain system,a slow propagation speed will lead to loss of the mined block and no reward(which is called orphaning[36]).The probability of orphaning is calculated as

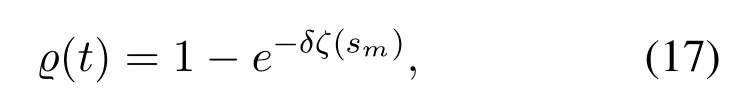
whereδis a constant,andζ(sm) indicates the propagation time for block sizesmof MEC serverm[8].Thus we obtain the probability of MEC servermsuccessfully mining a block as

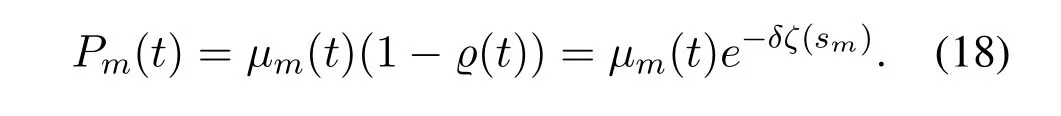
Denoterbas the mining reward for the winning MEC server.The expected mining payoffs of MEC servermcan be expressed as

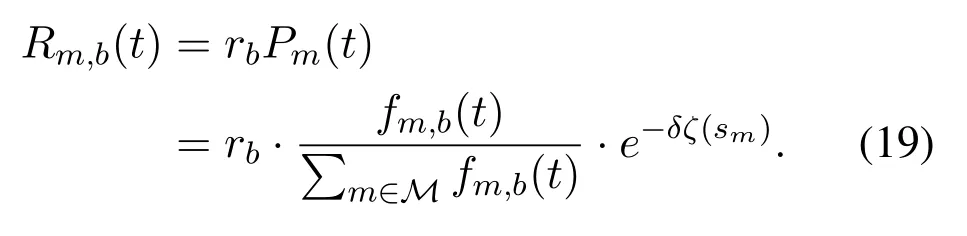
III.PROBLEM FORMULATION

In order to achieve a higher network revenue,achieve load balancing,and encourage MECS to participate in cooperative workloads execution,the MEC blockchain network operators need to make optimal decisions for workload offloading,service caching,load balancing among MECS,and computation capability allocation in each time slott.Let

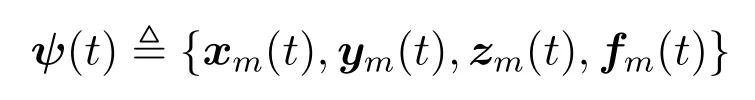
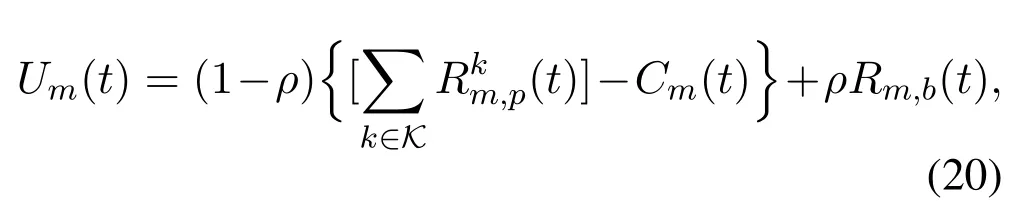
whereρ(greater than zero) is the weight parameter for the utility between the MEC system and the blockchain system.We formulate a problem that maximizes the weighted and time-averaged sum of network revenue in the long-term time horizon as

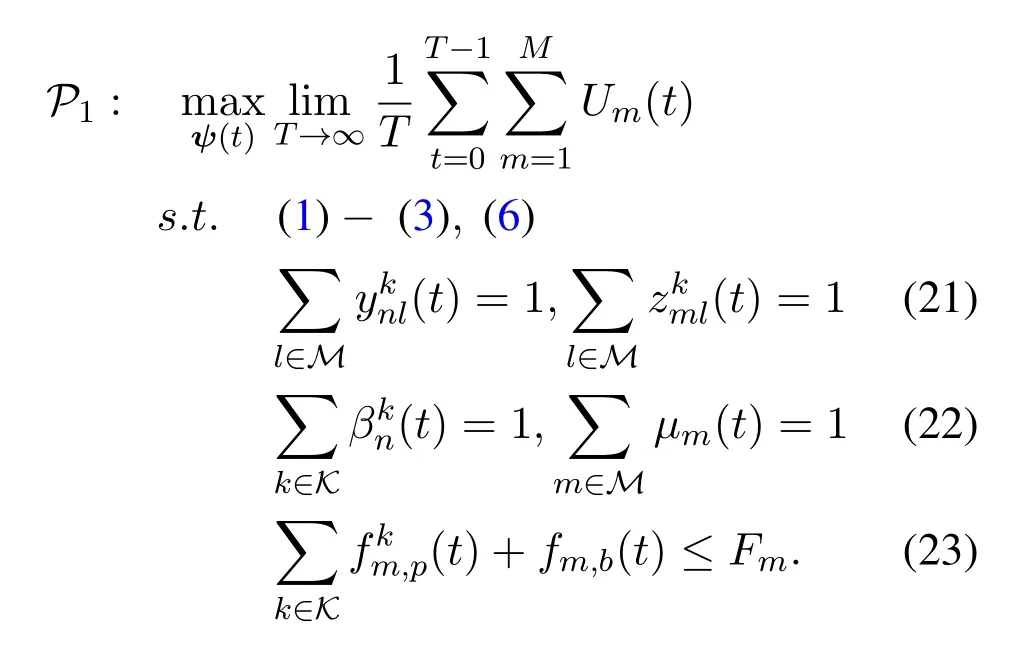
In ProblemP1,Constraint (1) represents the storage capacity constraint of MEC serverm.Constraint(2)describes that the relationship between service caching,workload offloading,and load balancing decisions.Constraint (3) shows the limit of overall bandwidth resources of MEC serverm.Constraint(6)enforces the limit of service capacity of the wireline LAN.Constraint (21) guarantees that the sum of the workload offloading decisions and the load balancing decisions of the MEC servermat time slottare both equal to 1.The first term in Constraints (22) guarantees the percentage of each type of workloads generated by MDnat time slott,and the second term of (22) indicates the limit of the proportional to the success of mining competition.Constraint (23) ensures that the sum of allocated computation capabilities for workload computing and mining service cannot exceed the computation capability of MEC servermat time slott.

Charles saw them both at the same time: the small white bird floating from among the park trees and the girl wheeling down the walk.1 The bird glided1 downward and rested in the grass; the girl directed the chair smoothly2 along the sunlit, shadowy walk.2 Her collapsible3 metal chair might have been motorized4: it carried her along so smoothly. She stopped to watch the ducks on the pond and when she shoved the wheels again, Charles sprang to his feet. May I push you? he called, running across the grass to her. The white bird flew to the top of a tree.

The formulated problem of long-term network revenue maximization is a mixed integer nonlinear programming(MINLP)problem.As the number of MDs in the MEC blockchain networks is increased,the complexity of the problem will also increase greatly,which is difficult to solve by traditional methods.Therefore,we propose a highly competitive solution based on DRL to drive the strategyψ(t).

IV.LEARNING-BASED JOINT SERVICE CACHING AND LOAD BALANCING POLICY

In this section,we consider ProblemP1as an MDP problem.We aim to design a learning-based joint service caching and load balancing policy to find a highly competitive solution to the original problemP1.

4.1 The DRL Framework

We first reformulate the problem as an MDP,and define the state,action,and reward function as follows.

4.1.1 State

4.1.2 Action

In the MEC blockchain network,we consider four types of actions,including service cachingxm(t),workload offloadingym(t),load balancingzm(t),and computation capability allocationfm(t).We denote

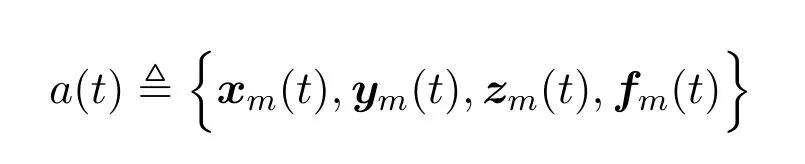
as the action space of MEC servermat time slott.To simplify the problem,we divide the number of workloads and service resources of the MEC serverminto countable parts to discretize the action space.

4.1.3 Reward Function

In this paper,we aim to maximize the network revenue by jointly optimizing the decisions for workload offloading,service caching,load balancing among MECS,and computation capability allocation.Therefore,the reward function needs to take these objectives into consideration,which is defined as

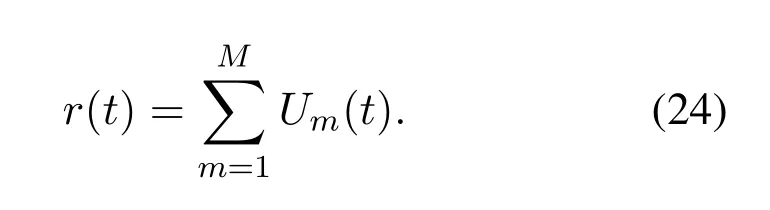
4.2 Learning-Based Algorithm

Reinforcement learning (RL) is used to describe and solve the problem of reward maximization or achieving specific goals through learning strategies in the process of interacting with the environment,usually described as an MDP.It is an autonomous learning process,where the agent makes decisions periodically and gradually,relying on the feedback from the environment to improve the strategy,until the best strategy

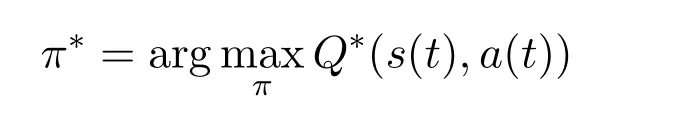
is learned.The agent aims to achieve the expected long-term reward,which can be expressed as:

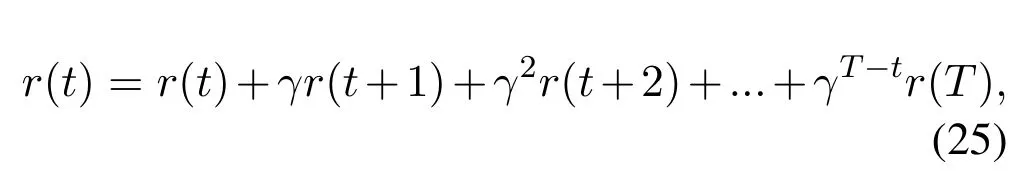
whereγ ∈[0,1] is the reward discount coefficient,indicating the influence of future rewards on the response of the current action.

DRL is an effective method to combine deep learning and RL to address problems with large action space and sample space,where a neural network called DQN is incorporated to approximate theQvalue.In the DQN architecture,for given system state and action inputs,the outputQvalue,Q(s(t),a(t))≈Q′(s(t),a(t);θ),can be obtained directly,whereθdenotes the parameter of the neural network.The neural network is trained by iteratively updating the parameterθto minimize the loss function:

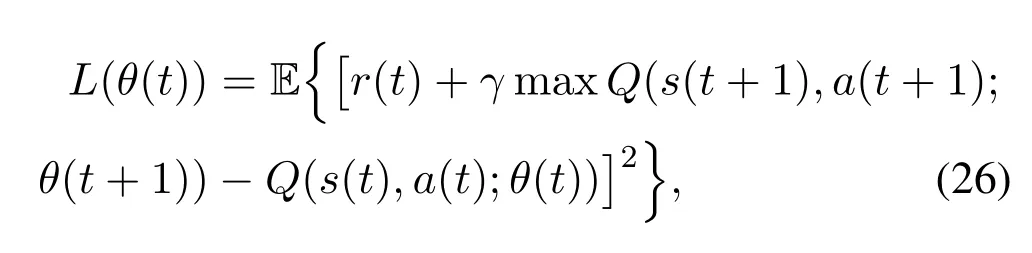
wherer(t)+γmaxQ(s(t+1),a(t+1);θ(t+1))is the targetQvalue and will be updated every once in a while.

To overcome theQvalue overestimation problem encountered in the DQN algorithm,we propose a double-dueling DQN based joint service caching and load balance algorithm.The key idea is to use different objective functions to select and evaluate actions,and then the target Q value in the double-dueling DQN can be expressed as:

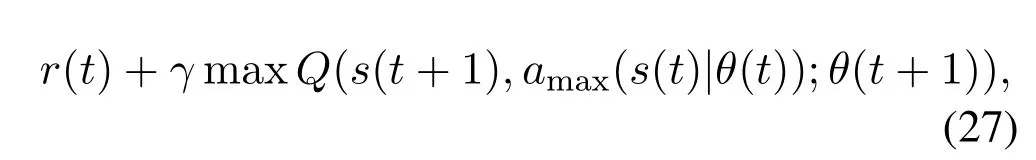
theamax(s(t)|θ(t))=arg maxa(t)Q(s(t),a(t);θ(t))is the best action,which is obtained through the current Q network.

TheQvalue is divided into two parts in the doubledueling DQN model.The first part is just based on the state and does not take into account the specific action to be performed,which is called value function and expressed asV(s).The second part is called advantage function and denoted asA(s,a),which is based on the current state and action.Thus,we obtain theQvalue in the double-dueling DQN architecture as

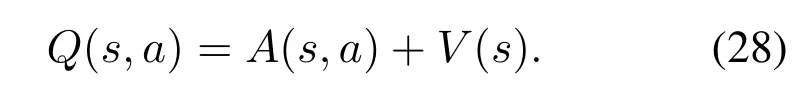
In the implementation of the proposed doubledueling DQN based joint service caching and load balance algorithm,we set a fully connected feed-forward 5-layer neural network,and each hidden layer has 20 neurons [37].In each training step,the state information in current system will be fed into theQnetwork.Then theQnetwork returns the optimal action,which is selected in accordance with theϵ-greedy policy.Based on the optimal action(service caching,workload offloading,load balancing,and computation capability allocation decisions),we can obtain the network utility by solving (27).And then we obtain the value of reward function by solving (20)and obtain the next states(t+1).All the experience(s(t),a(t),r(t),s(t+1)) in the training process will be accumulated in the experience replay poolD.A small group of samples will be selected from the pool to train the current network parameters,and the target network will be directly copied from the current network,with the same structure and parameters.The detailed algorithm is presented in Algorithm 1.

V.PERFORMANCE EVALUATION

5.1 Simulation Configuration

In this section,we validate the performance of our proposed algorithm by simulations using the Pytorch with Python 3.7 (tensorflow) on a desktop with Windows 64 bits,3.59 GHz AMD Ryzen 5 3600 6-Core Processor,and 16 GB RAM,and comparison with several baseline schemes.We consider an MEC blockchain networks including 30 MDs and 4 MECS.There are overlapping coverage areas between the MECS.Each MEC server serves a dedicated set of MDs that are associated with it.MDs can generate a total of four types of workloads.Assume that MECS have strong service capabilities to serve all types of workloads,and each MEC server can cache the corresponding application data in advance based on the caching policies.For each type of workload in the MEC system,the data size of each workload of typekisdk=[0.5,1]Mb/-workload,the required CPU cycles for processing one typekworkload ishk=[20,40]CPU cycles/Mb,and the required storage capacity isak=[20,80]GB.The storage capacity and computation capacity of MEC servers are set to [100,200] GB and [5,10] GHz,respectively.The channel gain for wireless data transmission is modeled by the indoor loss model[14]:

The noise powerσ2is-174 dBm/Hz[38].The weight factorφbetween delay and energy consumption are set to 0.6 and 0.4,respectively.For the blockchain network,η=1/600 sec [14] and the mining reward is set torb=20 tokens.Other simulation parameters are listed in Table 1.

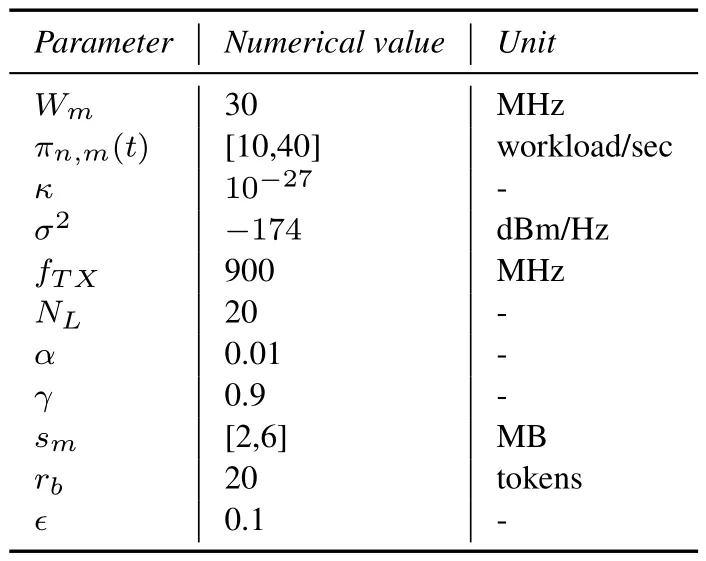
Table 1. List of simulation parameters.

We evaluate the performance of our proposed algorithm and compare it with the following baseline schemes under various system configurations:

1.No direct communications among MDs and their un-associated MECS (termed NDC): unlike our proposed scheme,in this scheme,the MDs in the overlapping coverage area of multiple MECS can only allow to offload workloads to its associated MEC server,and cannot directly offload workloads to other MECS that covering them.

2.Greedy offloading scheme (termed GO): in this scenario,each MEC server hopes to serve as many MDs as possible.As long as the MEC server caches the corresponding applications data to serve such type of workloads,the MEC server will reserve as many workloads as possible and ignore its computing capability and the current system state.For unserviceable workloads,the MEC server only considers the computing capability and ignores the reputation value when balancing the workloads to other MEC servers.

3.Random offloading scheme (termed RO): both MDs and MECS randomly select a feasible MEC server for workloads offloading with equal probability.

5.2 Results and Analysis

We first show the convergence of our proposed algorithm with respect to the loss function and learning rate in Figure 2 and Figure 3,respectively.In Figure 2,we present the convergence performance of the proposed algorithm as shown by the evolution of the loss function.At the beginning of the training process,since the double-dueling DQN agent does not have enough information to make reasonable decisions,the loss function assumes large values.As the training process goes on,the value of loss function decreases gradually and eventually approaches a relatively stable value after about 4,000 time slots.We then examine the influence of different learning rates on the convergence of the proposed algorithm in Figure.3.We simulate the change of reward function values atα=10-1,10-2,10-3over 12,000 time slots.The vertical axis is the long-term averaged reward value,which is normalized by introducingfor ease of viewing.It can be observed that the averaged reward value of the network gradually increases and approaches 1 as the learning process progresses.Furthermore,since the state of the network in each time slot may change dynamically,e.g.,due to the dynamic workload arrival process,the curve will still fluctuate slightly even after convergence.Moreover,as the learning rate is increased from 10-3to 10-1,the convergence rate of the proposed algorithm also increases gradually.

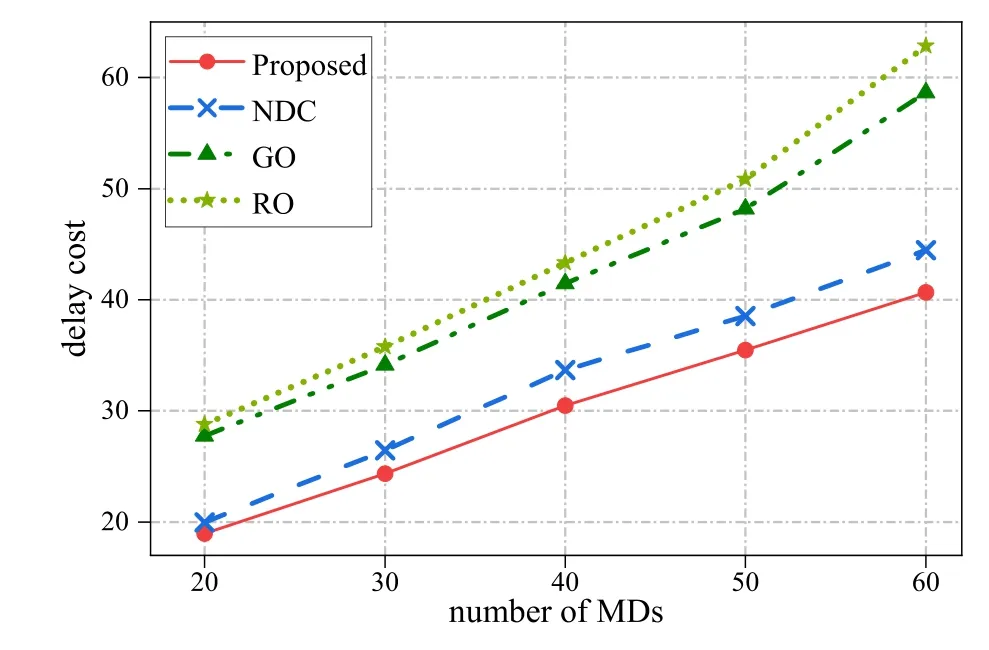
Figure 4. The network delay cost under different numbers of mobile devices.

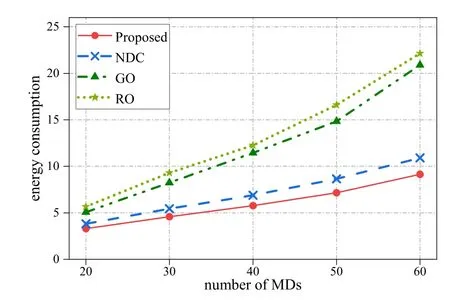
Figure 5. The Energy consumption under different numbers of mobile devices.

Next,we examine the network delay cost under different numbers of MDs.The results are presented in Figure 4.As the increase of the number of MDs,the amount of workloads will also increase.Due to the limited computation capabilities of MECS,all the four curves show high network delay costs.Compared with the three baseline schemes,our proposed algorithm achieves the smallest network delay costs.In the NDC scheme,each MD can only offload workloads to its associated MEC server,and then the MEC server may transfer the workloads to other MEC servers that can execute the workloads.Such an approach increases the data transmission delay between MECS.Thus,the network delay cost is slightly higher than our proposed algorithm.In addition,the GO scheme offloads workloads to the MEC server with the largest computational capability other than itself.Thus its network delay cost is lower than that of the RO scheme.

We also demonstrate the energy consumption of the four schemes under different numbers of MDs in Figure 5.It can be seen that the energy consumption trends of the four algorithms are similar to the network delay cost trends shown in Figure 4.

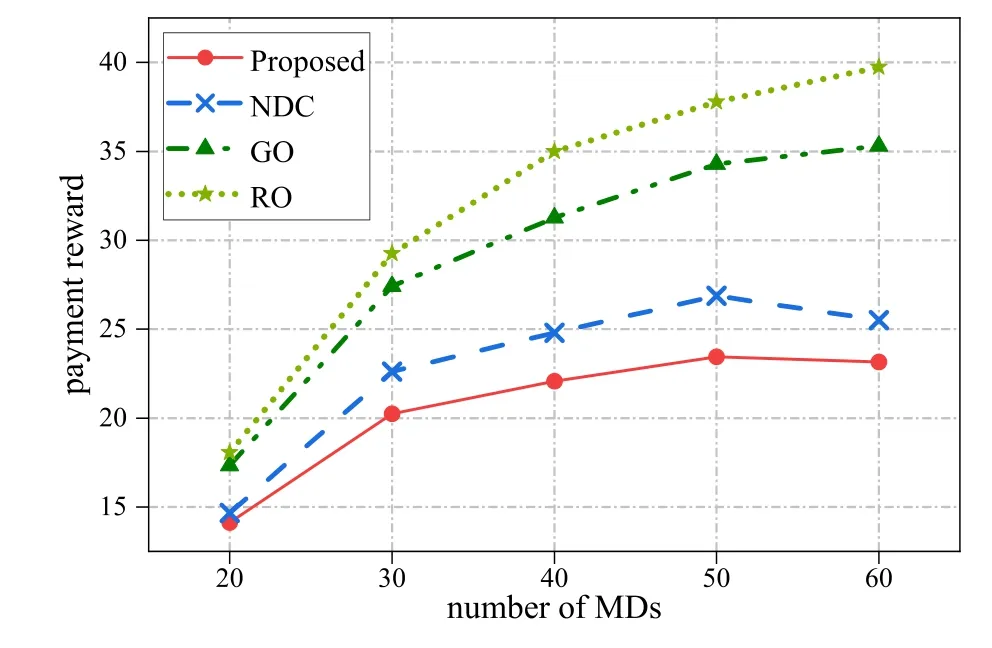
Figure 6. The Payment reward under different numbers of mobile devices.

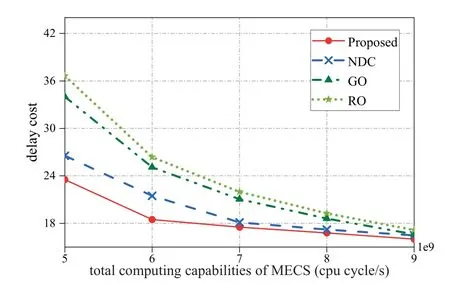
Figure 7. Delay cost versus total computational capability.

Figure 6 verifies the effect of different numbers of MDs on the payment rewards received by MEC servers.According to (15),the payment rewards of each MEC server are related to the credibility evaluation results of each MEC server provided by MDs and the amount of workload processing.As the number of MDs is increased,the amount of workloads increases,and the payment rewards of the four algorithms all become larger.However,due to the constant increase in the number of MDs on the premise of maintaining the same computing capabilities of MECS,the network delay cost gradually increases(as shown in Figure 4),which leads to poorer credibility evaluation results of MECS.Thus,the trends of payment rewards for the four algorithms will slow down or even decrease when the number of MDs becomes large.

Next,we examine the effect of different total computation capabilities of MECS on the network delay cost and the energy consumption of MECS in Figure 7 and Figure 8,respectively.Figure 7 shows the decreasing network delay cost as the total computation capabilities of MECS are increased.It can be seen that when the computing capabilities of MECS are sufficient to process the current workloads,the decrease of the network delay cost gradually slows down in all the curves of the four algorithms.Figure 8 shows that the energy consumption increases with the computing capabilities of MECS.

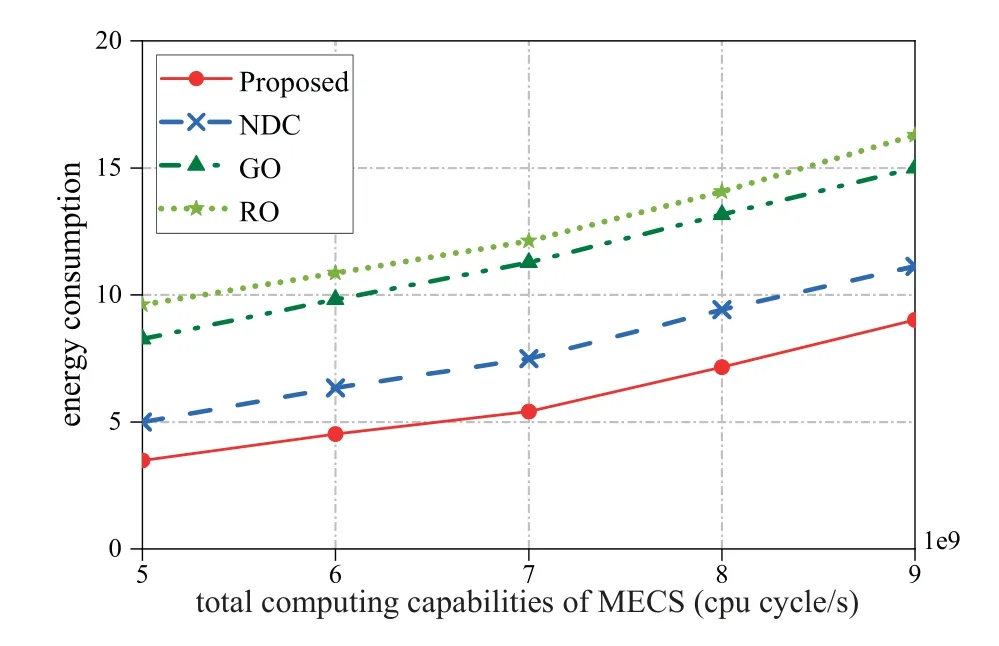
Figure 8. Energy consumption vs.computing capability.

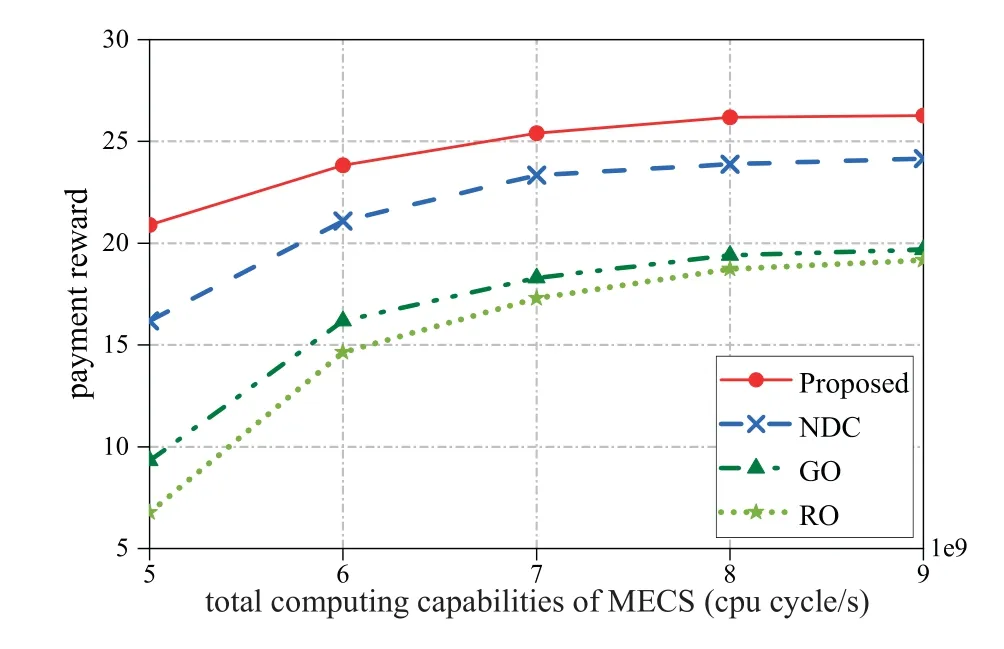
Figure 9. Payment reward vs.computational capability.

In Figure 9,we present the relationship between the payment reward obtained by the MECS and the total computing capabilities.According to (15),when the MEC server processes the same amount of workloads,a better value of credibility evaluation will provide the MEC server a higher payment reward.As the computing capabilities of MECS is increased,the processing delay gradually decreases,and the credibility evaluation results of MECS gradually become better.Thus,as the MECS computing capabilities are increased,the payment rewards obtained by the MECS get better and better.When the computing capabilities of MECS are sufficient to meet the current workloads,the payment rewards obtained by the MECS will be gradually stabilized.

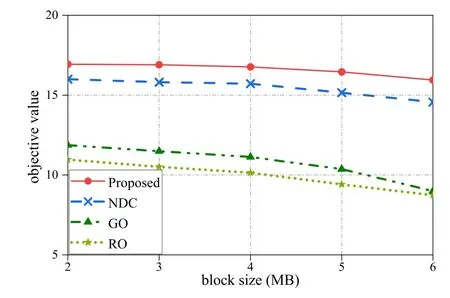
Figure 10. Objective function value vs.block sizes.

Figure 10 shows the influence of the current block size on the value of the objective function.According to (20),the value of the objective function is related to the mining payoffs of MECS.A larger block size value leads to a longer propagation time for the corresponding block,which is more likely to be lost during the propagation process.Therefore,the probability of success of block mining will becomes smaller.And thus the objective function values of the four algorithms decrease gradually with the increase of block size.

VI.CONCLUSION

In this paper,we considered the problem of joint service caching and load balancing for blockchainauthorized MEC networks with multiple cooperative MECS and multiple types of workloads.We established a secure load balancing mechanism among cooperative MECS based on the blockchain technology to maximize resources utilization.We formulated a long-term network revenue maximization MDP problem and developed a double-dueling DQN algorithm for network revenue maximization while satisfying the requirements of MDs.We analyzed the convergence and feasibility of the proposed algorithm by extensive simulations.Compared with three baseline schemes,our proposed algorithm achieved a superior performance in terms of the energy consumption,the network delay cost,and the payment reward in MEC blcokchain networks.

ACKNOWLEDGMENT

This work was supported in part by the National Natural Science Foundation of China 62072096,the Fundamental Research Funds for the Central Universities under Grant 2232020A-12,the International S&T Cooperation Program of Shanghai Science and Technology Commission under Grant 20220713000,the Young Top-notch Talent Program in Shanghai,the“Shuguang Program”of Shanghai Education Development Foundation and Shanghai Municipal Education Commission,the Fundamental Research Funds for the Central Universities and Graduate Student Innovation Fund of Donghua University CUSF-DH-D-2019093.S.Mao’s research is supported in part by the NSF under grants CNS-2107190 and ECCS-1923717.