基于惯性—地磁组合的多模型融合姿态测量算法*
邵艳巡, 邓林红, 戎海龙
(1.常州大学 计算机与人工智能学院 阿里云大数据学院,江苏 常州 213164; 2.常州大学 生物医学工程与健康科学研究院,江苏 常州 213164; 3.常州大学 机械与轨道交通学院,江苏 常州 213164)
0 引 言
惯性—地磁组合测量单元由于具有无需外界参考即可获得运动体姿态的优势而被应用于人体姿态跟踪领域[1,2](包括虚拟现实和体育运动等)和生物医学领域[3](包括医疗康复和手术器械跟踪等)。惯性—地磁组合测量单元由微机电系统(micro-electro-mechanical system,MEMS)传感器组成,包括三轴陀螺仪、三轴加速度计和三轴磁强计,测量得到的数据用于运动体姿态测量。
早期研究发现,单独使用陀螺仪结合测量算法可以获得运动体姿态,如四元数微分算法[4],但由于陀螺仪随机误差的影响使静态出现发散现象,所以此类算法动态精度较高,静态精度较差。对应地,使用加速度计和磁强计结合测量算法也可以获得运动体姿态,如QUEST算法[5]和LMA算法[6]等,但由于运动体线性加速度和周围磁场干扰使动态出现误差,所以此类算法静态精度较高,动态精度较差。为了得到动静态性能兼顾的算法,近期研究主要是将3种传感器数据通过融合姿态测量算法获得姿态角,此类融合算法主要包括扩展卡尔曼滤波(extended Kalman filtering,EKF)算法[7]和互补滤波(CF)算法[8],为了消除线性加速度和周围磁场的干扰,获得准确的运动体姿态,研究者主要从算法公式上改进,例如文献[9]提出的QEKF(quaternion-based EKF)算法、文献[10]提出的LMA-CO(LMA-complementary)算法以及文献[11]提出的GCF(generalized linear quarternion complementary filtering)算法等。
为了进一步提升现有CF算法的性能,本文提出了一种基于惯性—地磁组合的多模型融合姿态测量算法。将一段连续的运动分为动态段和静态段处理,最后将每段的姿态测量结果组合在一起得到此段连续运动的姿态。
1 算法总体框架
本文运动体姿态测量的流程如下:首先,通过惯性—地磁组合测量单元获得数据;然后,通过可靠性判定准则将每个时刻的运动状态分类并识别;接着,确定每种运动状态下传感器数据的可靠性,并建立数据融合模型;最后,利用数据融合算法获得姿态角。
2 数据提取
本文选用Xsen公司的惯性测量单元MTi传感器模块采集数据,选用POLHEMUS公司的Long Ranger电磁跟踪系统同步测量姿态角作为实验基准。惯性测量单元MTi和Long Ranger电磁跟踪系统的采样频率分别为256 Hz和240 Hz。当地重力加速度gn为9.783 m/s2,当地地磁场强度h为0.862 5 μT,当地磁倾角θ为32°。
3 运动状态分类与识别
3.1 运动状态分类
对于一段连续运动,本文将其分段处理:动态段和静态段。其中,静态段又分为有磁干扰和无磁干扰2种情况,于是将运动状态分为3种,分别为无磁静态、有磁静态和动态。利用可靠性判定准则实现运动状态分类及识别。3种运动状态的判定准则如下:1)无磁静态的可靠性判定准则为:|‖a(k)‖-‖gn‖|≤ε1&‖G(k)‖≤ε2&|‖m(k)‖-‖h‖|≤ε3;2)有磁静态的可靠性判定准则为:|‖a(k)‖-‖gn‖|≤ε1&‖G(k)‖≤ε2&|‖m(k)‖-‖h‖|>ε3;3)动态的可靠性判定准则为:|‖a(k)‖-‖gn‖|>ε1‖‖G(k)‖>ε2。其中,a(k)为k时刻的加速度,m(k)为k时刻的磁场强度,G(k)为k时刻的角速度,gn为当地重力加速度,h为当地地磁场强度,ε1,ε2和ε3分别为加速度阈值、角速度阈值和磁场强度阈值。
3.2 运动状态识别
从上一节中的可靠性判定准则公式发现,影响运动状态识别的主要因素有2个:1)传感器测量值选择;2)最优阈值选择。
3.2.1 传感器测量值选择
本文采用加速度计、磁强计和陀螺仪本时刻测量值及前4个时刻的测量值的平均值作为加速度计、磁强计和陀螺仪本时刻的测量值。公式如下
a(k)=(a(k)+a(k-1)+a(k-2)+a(k-3)+
a(k-4))/5,k≥5
(1)
m(k)=(m(k)+m(k-1)+m(k-2)+m(k-3)+
m(k-4))/5,k≥5
(2)
G(k)=(G(k)+G(k-1)+G(k-2)+G(k-3)+
G(k-4))/5,k≥5
(3)
3.2.2 最优阈值选择
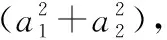
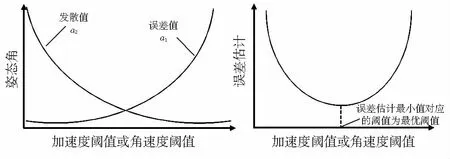
图1 误差值、发散值和误差估计随加速度(或角速度)阈值变化示意
4 数据融合模型建立与切换
本文定义了3种数据融合模型,分别为:AM模型、GA模型和G模型,并分别对应无磁静态、有磁静态和动态。当识别为无磁静态时,加速度计和磁强计数据可靠,而陀螺仪数据不可靠,则舍弃陀螺仪数据,仅用加速度计和磁强计数据进行融合获得姿态角,定义为AM模型;当识别为有磁静态时,只有加速度计数据可靠,磁强计和陀螺仪数据均不可靠,但由于加速度计数据只能求得俯仰角和滚转角,无法得到偏航角,此时根据充分利用原则,由于存在磁场干扰无法使用磁强计数据获得偏航角,只能用陀螺仪来估计航向,所以在此情况下,仍然使用陀螺仪数据计算得到偏航角,于是有磁静态用于姿态测量的数据为加速度计和陀螺仪数据,定义为GA模型;当识别为动态时,加速度计和磁强计数据都不可靠,用于姿态测量的数据只有陀螺仪数据,定义为G模型。如图2为不同数据融合模型。
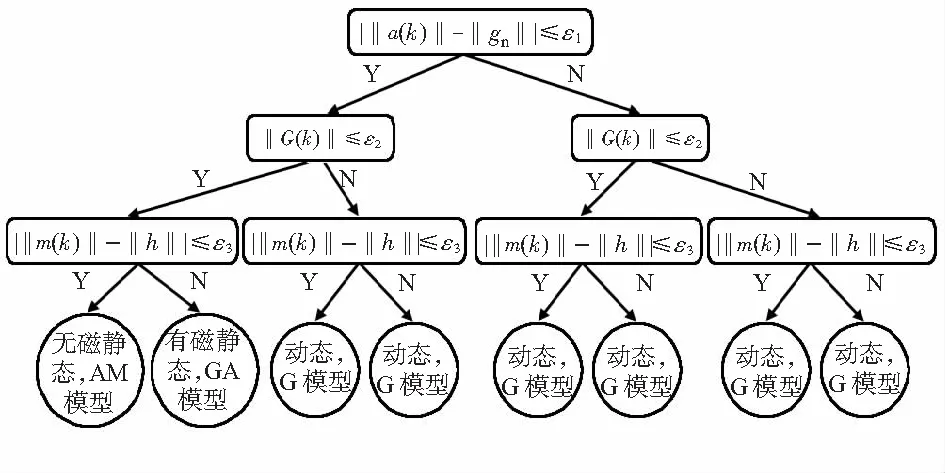
图2 数据融合模型
5 融合姿态测量算法设计
QUEST算法[5]是基于Wahba问题提出的一种矢量定姿算法。本文首先使用QUEST算法融合加速度计和磁强计数据,获得方向余弦矩阵C2,然后利用四元数微分方程[4]处理陀螺仪数据,获得方向余弦矩阵C1,并结合融合姿态测量算法,得到最终的方向余弦矩阵C,并获得姿态角。针对有无磁场干扰,在利用QUEST算法融合加速度计和磁强计数据获得方向余弦矩阵时分为2种情况:1)无磁干扰时,加速度计和磁强计数据均可靠,可用于姿态测量,通过计算得到方向余弦矩阵为C21;2)有磁干扰时,磁强计数据不再可靠,即不能用于姿态测量,所以此时要将QUEST算法中,磁强计的占比系数设为0,使得只有加速度计数据参与姿态测量,通过计算得到的方向余弦矩阵为C22。
本文使用的融合姿态测量算法公式为
C=α×C1+(1-α)×C2
(4)
式中α为权重,C2根据上述情况取C21或C22。
不同的运动状态使用不同的传感器数据完成姿态测量,对应第4章中不同的数据融合模型,当识别为无磁静态时,用于姿态测量的数据为加速度计和磁强计数据,此时式(4)中α为0,则C=C21。同理当识别为有磁静态时,用于测量俯仰角和滚转角的数据为加速度计数据,此时α为0,则C=C22,由于加速度计数据不能求得偏航角,所以根据充分利用原则,在此状态下利用陀螺仪数据进行偏航角测量,此时α为1,则C=C1。同样地,当识别为动态时,用于姿态测量的数据为陀螺仪数据,此时α为1,则C=C1。
6 实验仿真
6.1 无磁场干扰动态实验
首先将安装有惯性—地磁组合测量单元的实验装置在水平桌面上静止一段时间,然后进行往复三维运动,一段时间后再次静止于水平桌面上。
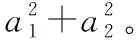

图3 无磁场干扰动态实验
取文献[11]提出的GCF算法、文献[10]提出的LMA-CO算法和文献[9]提出的QEKF算法作为实验对比算法。图3(c)为本文算法与其他算法得到的姿态角与参考姿态角对比结果。表1为本文算法与GCF、LMA-CO和QEKF算法的姿态角均方根误差(RMSE)。从图3(c)和表1中分析发现,本文算法与GCF算法相比,姿态角精度有明显的提高,与LMA-CO算法和QEKF算法相比滚转角和俯仰角精度明显提高。

表1 不同算法的RMSE(°)
表2为本文算法与其他算法单位采样点时间消耗,从表中发现本文算法时间消耗最低,即速度最快。
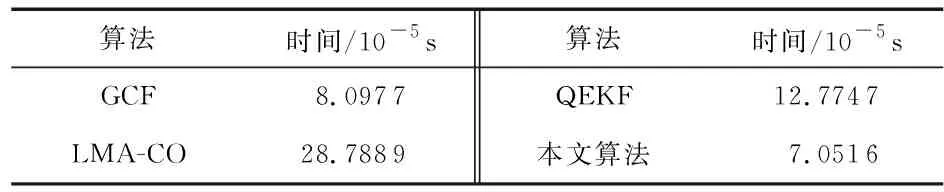
表2 不同算法单位采样点时间消耗
6.2 有磁场干扰静态实验
将安装有惯性—地磁组合测量单元的实验装置置于水平桌面上,手持手机在MTi旁边不停晃动,人为制造磁场干扰。图4为磁干扰下静态实验的姿态角误差,由于识别为有磁静态时,用于姿态测量的只有加速度数据,已知加速度数据只能求得滚转角和俯仰角,不能求得偏航角,所以,此状态下根据充分利用原则,偏航角使用陀螺仪数据求得,虽然误差较大,但总好于无偏航角结果。从图中发现滚转角误差和俯仰角误差均小于0.4°。
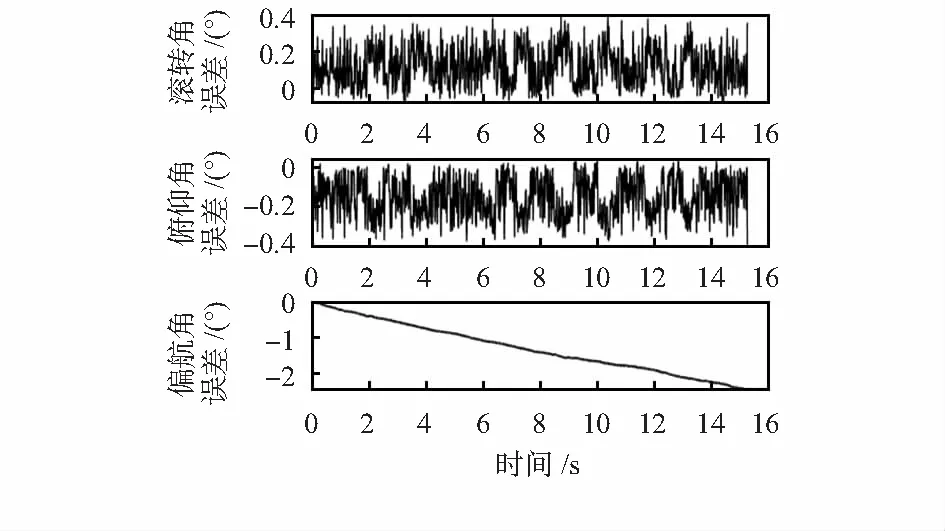
图4 有磁静态过程的姿态角误差
7 结 论
基于惯性—地磁组合测量单元的实验结果对比表明:本文提出的算法与现有CF算法相比,既提高了精度,也提升了速度,与现有EKF算法相比滚转角和俯仰角的精度都有明显提高。

