基于CEEMDAN-IGWO-BP的供热管道泄漏孔径预测*

王 阳， 仪垂杰， 赵 鹏， 张 强， 刘尊民

(1.青岛大学 自动化学院, 山东 青岛 266071； 2.青岛理工大学 机械与汽车学院,山东 青岛 266520； 3.工业流体节能与污染控制教育部重点实验室，山东 青岛 266520)

0 引 言

供热管道是建设现代化城市的关键设施，一旦发生泄漏，不仅会造成经济损失，而且会带来严重的环境污染[1,2]。由于管道受自然腐蚀导致的泄漏大多数是从微小泄漏开始的，因此，对管道的微小泄漏进行实时监测及泄漏程度的判断极为关键[3]。

目前，相关学者针对管道泄漏故障诊断技术已有较多研究，文献[4～6]利用负压波对管道泄漏进行识别，但负压波对微小泄漏产生的压力变化反应不灵敏，无法对管道微小泄漏进行有效监测；焦敬品等人[7]提取泄漏声信号的时域、频域、形状等特征参数，利用反向传播(back propagation,BP)神经网络识别管道泄漏类型，该方法提取了过多的特征，使得BP神经网络本身存在的训练时间长、易早熟收敛等问题更加突出；文献[8,9]分别采用小波包和经验模态分解(empirical mode decomposition，EMD)对管道泄漏信号时间序列进行分解，降低了泄漏信号的非平稳特征，而小波分解存在需人为选择小波基函数与分解层数的缺陷，虽然EMD克服了这些缺陷，但分解后的固有模态函数(intrinsic mode function,IMF)分量仍存在模态混叠现象。上述研究大多针对管道泄漏工况的分类与识别问题，如何进一步根据管道复杂环境建立泄漏孔径与管道运行参数之间的映射模型仍是难点问题。

针对上述问题，首先,使用对泄漏信号较为敏感的声波来完成对管道微小泄漏的监测；然后,利用自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)[10]对泄漏信号进行分解，通过相关系准则筛选有效分量，并使用能量矩提取特征；进一步，提出改进灰狼优化(improved gray wolf optimizer，IGWO)算法，并在基准测试函数上验证了改进策略的有效性；最后,建立IGWO-BP预测模型，并利用实验平台中不同孔径泄漏信号的特征参数对预测模型进行训练测试。结果表明，本文提出的预测模型误差较小，能够精确预测管道的泄漏孔径。

1 特征提取方法

1.1 CEEMDAN

泄漏信号x(t)经过CEEMDAN后，可以分解成为K阶IMF分量cK(t)和信号残差r(t)的和

(1)

经过CEEMDAN的各个IMF突出了数据的局部特征,对其进行分析可以更准确有效地把握泄漏信号的特征信息。

1.2 基于相关系数的筛选准则

IMF与原始信号的相关系数表示为

(2)

1.3 能量矩特征提取方法

管道泄漏的状态不同，其声信号能量所处的频带会产生变化，能量矩是一种考虑了时间尺度的特征提取方法，相较于传统的能量特征提取方法更能表征原始信号的能量分布，其进行特征提取的具体过程如下：

首先,通过CEEMDAN与相关系数筛选准则得到可以表征泄漏信息的IMF，进一步对筛选后的IMF进行能量矩计算

(3)

其中，Ek为第k个IMF的能量矩，Δt为采样间隔，Dkj为第k个IMF在第j个采样点的幅值；n为采样点的个数。

归一化能量矩阵特征向量T如下

(4)

2 IGWO算法与验证分析

2.1 灰狼优化算法

灰狼优化(gray wolf optimization,GWO)算法[11]是受自然界中灰狼种群的领导阶级制度和种群狩猎方式启发的群体优化算法，其按照适应度值将灰狼种群分为4个阶级：α，β，δ，ω，分别等同为最优解、优解、次优解以及候选解，并通过狼群捕猎时，ω狼在不断识别猎物位置的同时，且向着α，β，δ狼包围圈不断靠近的行为来模拟寻找全局最优解的过程。GWO算法的详细数学模型见文献[11]。

2.2 IGWO算法

1)Bernoulli混沌映射初始化种群

在GWO算法中，灰狼个体位置向量初始化是随机的，不能保证灰狼种群在求解空间上的均匀分布。为改善灰狼个体位置随机初始化问题，提高算法的求解速度与质量，引入Bernoulli混沌映射初始化灰狼个体位置，其表达式为

(5)

本文取λ=0.4，此时Bernoulli映射所得序列均匀分布，对不同的映射值具有近似一致的分布密度。

2)改进控制参数更新策略

在GWO算法中，收敛因子A随着控制参数a而变化，当|A|>1时，狼群在整个狩猎区域内搜寻目标，当|A|<1时，狼群不断包围最优猎物。在GWO算法中，控制参数a线性递减，而GWO算法的寻优过程是非线性的，使用线性更新策略并不能使GWO算法的全局搜索能力和局部开发能力发挥到最大化，相反还有可能陷入局部最优问题。

本文提出的基于椭圆规律变化的控制参数更新策略，如式(6)所示

(6)

式中tmax为最大迭代次数，相较于改进前的控制参数更新策略，在迭代前期，控制参数a递减速率较慢，改善了算法的全局探寻能力，在迭代后期，控制参数a递减速率加快，增强了算法在局部区域的搜索精度。

3)改进自适应位置更新策略

在GWO算法中，灰狼个体每次的更新位置是由α，β，δ狼的位置赋予相同权重得来的，但是α，β，δ狼的特征和决策能力不同，这就使得原始的GWO算法收敛速度较慢，同时在GWO算法中，α，β，δ被初始化后，只有在迭代过程中出现适应值优于它们的解时才会被更新，而当α，β，δ全都陷入局部最优时，整个种群无法得到全局的最优解。

本文结合文献[12]与文献[13]的动态权重更新策略，提出了基于自适应和适应度相结合的自适应动态权重位置更新策略，公式如下

(7)

(8)

(9)

其中，Xi为当前ω狼需要向α，β，δ狼更新的移动距离，Wi为ω狼到三者的位置权重，fj分别为α，β，δ狼的适应度值。灰狼个体每轮的更新位置如式(9)。

2.3 IGWO算法的性能验证

本文选取了2个单峰测试函数：Sphere(F1)、Schwefel2.22(F2)和2个多峰测试函数：Generalized Griewank(F3)、Ackley(F4)分别利用GWO算法、粒子群优化(particle swarm optimization,PSO)算法、基本教与学(TLBO)算法以及本文的IGWO算法进行仿真测试。

仿真测试中将所有算法的种群规模设置为30，最大迭代次数设置为500。其中，将PSO算法的速度更新参数c1，c2设置为2。每个算法均单独运行20次，取最典型的结果。4种算法在4个测试函数上的收敛曲线与迭代结果分别如图1和表1所示。

图1 4种算法在测试函数上的收敛曲线

从图1中可以看出，本文提出的3种改进策略对GWO算法的性能有大幅度的提升，IGWO算法在4个测试函数上均以最快的速度收敛到理论最优值，在表1中，从仿真测试结果的平均值中看出，IGWO算法的收敛精度优于其他算法，全局寻优能力更佳，同时，在各个测试函数结果的标准差中可以看到，IGWO算法具有更好的稳定性。

表1 测试结果

3 泄漏孔径预测模型构建

基于本文提出的GWO算法改进策略，把训练后预测模型的平均绝对误差(mean absolute error,MAE)作为IGWO算法的适应度函数，利用IGWO算法的全局寻优能力找到BP神经网络的最优初始权值和阈值，从而提高预测模型对管道微小泄漏孔径的预测精度。IGWO-BP神经网络模型对管道泄漏孔径进行预测的流程如图2所示。

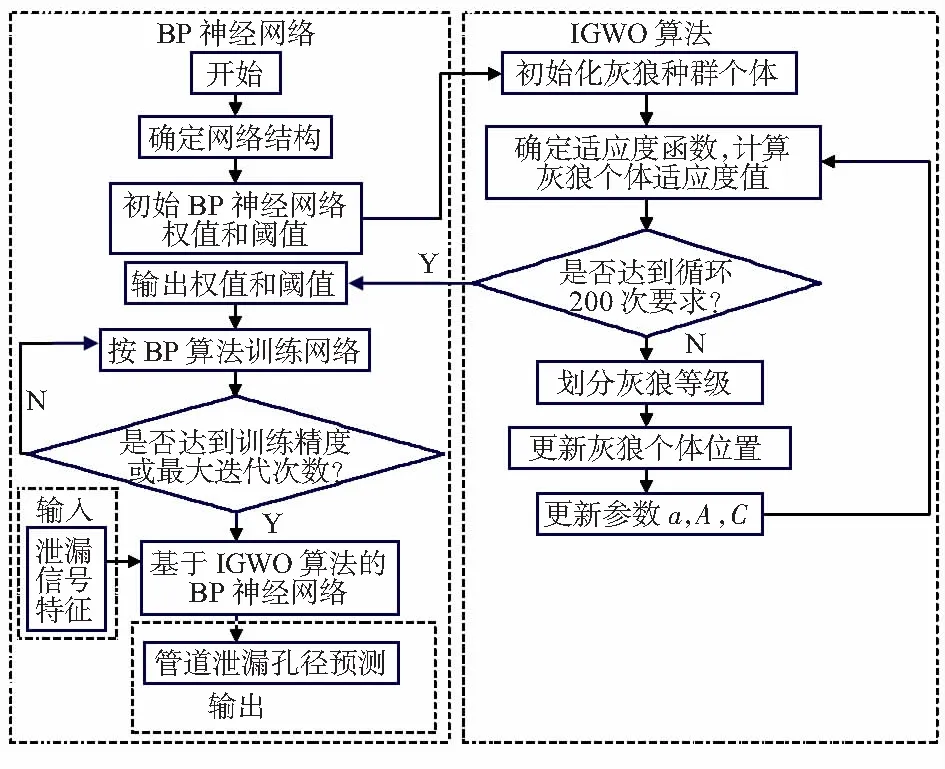
图2 泄漏孔径预测流程

4 实验分析

4.1 测试平台

利用实验室管道泄漏监测平台的泄漏信号数据对其进行验证。实验时，控制管壁的压力，通过开启安装有不同开孔孔径堵头的球阀来模拟不同孔径的泄漏情况，2组次声传感器嵌入管道内并连接到数字化仪采集管道泄漏信号，采样频率为2 kHz。

4.2 泄漏信号预处理

首先采集管壁压力分别为0.05,0.1,0.2,0.3 MPa；泄漏孔径在0.5～8 mm时不同位置的信号共500组(训练集与测试集的比例为7︰3)。管道压力为0.3 MPa ，泄漏孔径为5 mm的泄漏信号的原始序列如图3所示。利用CEEMDAN对泄漏信号进行分解并筛选出相关系数位于前5位的IMF,如图3所示。

图3 管道泄漏信号及其有效IMF

对不同工况下的泄漏信号分解出的有效IMF按照相关系数从小到大的顺序分别计算能量矩并进行归一化处理，得到的能量矩特征向量如图4所示。

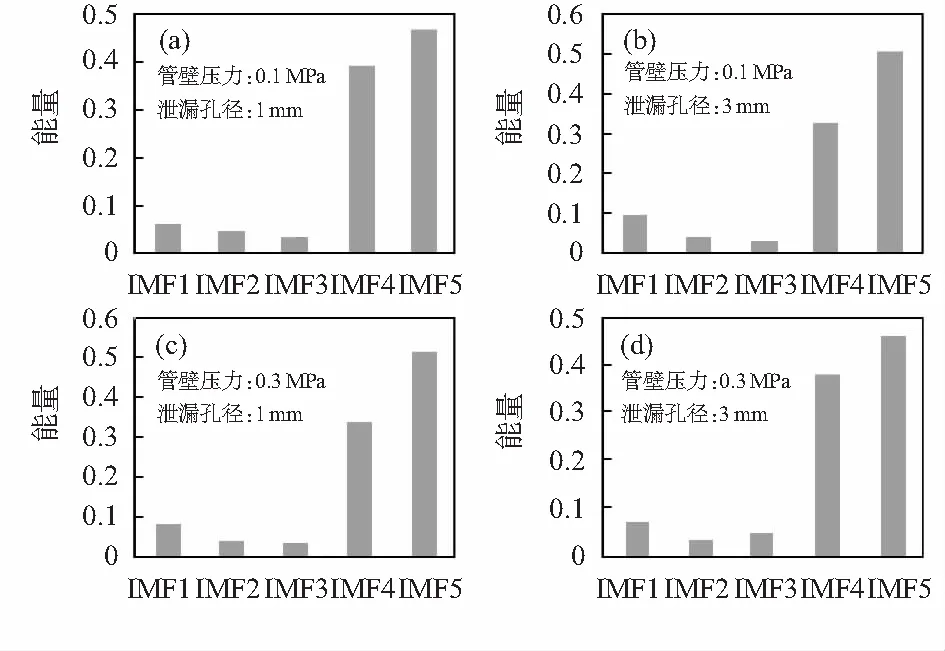
图4 能量矩特征向量分布

通过对比上述泄漏信号的能量矩分布特征，可以发现，在相同管壁压力下，泄漏孔径不同，各IMF的能量占比不同，具有表征泄漏孔径的能力。当管壁压力、泄漏孔径均不相同时，经归一化后的能量矩占比可能会相似，此时单凭能量矩无法正确表征泄漏孔径，因此，管道压力是影响泄漏信号能量占比的主要因素之一。综上所述，本文选取了能量矩特征向量以及管壁压力做归一化后作为预测模型的输入，将泄漏孔径作为输出。

4.3 基于IGWO-BP模型对泄漏孔径预测

本文将BP神经网络的输入节点设置为6个，隐含层节点设置为12个，输出节点设置为1个。同时设定训练次数为200次，目标精度为0.001，学习率为0.01；各优化算法的种群规模设置为30，迭代次数为500，各模型均独立运行30次，取最典型结果，5种神经网络模型预测泄漏孔径的误差分布对比如图5所示。

图5 各预测模型的预测误差对比

由图6可见，未经优化的BP网络预测误差较大且稳定性不足，而IGWO-BP模型的预测误差均在±0.1 mm之间，尽管GWO-BP、TLBO-BP、PSO-BP的预测模型相较于BP预测模型均有不同程度改善，但预测效果仍劣于IGWO-BP预测模型，这验证了IGWO算法的全局寻优能力与局部搜索精度性能。

本文引入平均绝对百分比误差(mean absolute percen-tage error,MAPE)与均方根误差(root mean square error,RMSE)2种评价指标对5种预测模型的精度进行对比，如表2所示。可知，在实验条件相同的情况下，IGWO-BP预测模型的MAPE与RMSE在5种预测模型中最小。

表2 各预测模型的MAPE与RMSE对比

4种优化算法的适应度值收敛曲线如图6所示。可以看到， IGWO-BP模型在405次迭代后仍然在收敛，没有陷入局部最优；同时，IGWO-BP模型具有最大的适应度值收敛幅度，达34.7 %，表明该方法在提升优化BP神经网络预测精度方面具有优越性。

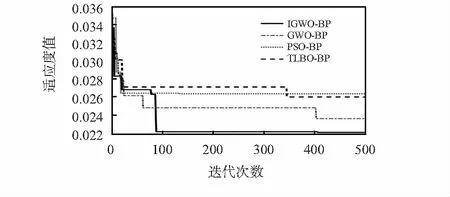
图6 适应度值收敛曲线

5 结 论

针对埋地管道微小泄漏孔径的预测问题，首先,提出一种基于CEEMDAN与能量矩的特征提取方法;然后,通过IGWO-BP神经网络建立了泄漏孔径预测模型;最后,使用实验室平台的管道泄漏信号对预测模型进行了训练和预测验证。实验结果表明：本文提出的预测方法能够准确预测管道在自然腐蚀情况下泄漏初期的微小泄漏程度，为避免后续泄漏程度加重以及指导管道泄漏的补救工作提供参考。