基于锚点策略的快速无监督特征选择算法*
朱建勇, 徐 彬, 杨 辉, 聂飞平
(1.华东交通大学 电气与自动化工程学院,江西 南昌 330013; 2.江西省先进控制与优化重点实验室,江西 南昌 330013; 3.西北工业大学 计算机科学学院 光学影像分析与学习中心, 陕西 西安 710072)
0 引 言
网络信息技术的发展迅速扩大了信息数据样本的数量和维度,数据模型也逐渐呈现出高度复杂的特征[1]。从高维数据中提取有用的关键信息现在成为数据挖掘、计算机视觉、机器学习等领域的研究热点。在特定的应用中,如人脸识别[2]、文本检索[3]、图像分类[4]等,高维数据给信息存储带来了巨大的压力。特征选择是应对数据“维数灾难”的典型方法,特征选择在样本的原始特征空间中筛选具有代表性的特征子集,没有改变特征属性。依据是否利用数据标签,特征选择可分为有监督特征选择[5]、半监督特征选择[6]和无监督特征选择[7]。有监督和半监督特征选择可以根据数据的标签信息对模型进行训练,选择代表性的特征子集相对简单有效,无监督特征选择则是从整个特征集合中选择特征,而无需使用标签信息。一般来说,在大多数实际情况下获得的都是未标记的数据,此时标记大量高维度数据是不划算和不现实的[8]。在这类场景中,无监督特征选择方法是一个可靠的选择。
根据特征评价和选择中特征结合方式归类,特征选择方法主要分为3类:过滤式方法、包裹式方法和嵌入式方法。嵌入式方法用于处理大规模数据时效率高、效果理想,受到研究者的青睐。由于局部结构能更好地反映数据的实际情况,大多数嵌入式特征选择方法都是探索局部流形结构。真实数据的稀疏性使得研究者将稀疏结构学习引入到特征学习算法的框架中。Liu W等人[9]利用稀疏学习决策树方法实现了对高维数据的预测,提高了算法的鲁棒性和稳定性。传统的基于图的特征选择方法通常需要经过两个步骤:探索数据结构构造相似度矩阵,利用稀疏正则化方法选择具有代表性的特征。
传统的谱方法[10]往往使用K近邻法来构造几乎满秩的相似矩阵,这使得图的构造和谱分析非常耗时,且时间复杂度至少为O(n2d)。为了降低算法的计算复杂度,加快相似矩阵的构造,受构造可伸缩大图[11]的启发,采用锚点嵌入策略构造稀疏相似矩阵。该方法的计算复杂度为O(nd),大大加快了相似矩阵的构造速度。稀疏正则化选择特征的正则项研究者通常倾向于使用L2,1范数,Yang Y等人[12]将结构学习与特征选择相结合,利用判别分析特征的重要性来选择特征。Han K等人[13]也提出使用L2,1范数对编码器的权重进行稀疏正则化。值得注意的是,这些算法在优化L2,1范数时不可避免会引入正则化参数,带来复杂的调参问题。
为此,本文提出了一种基于锚点策略的快速无监督特征选择(fast anchor-based unsupervised feature selection,FAFS)算法。该算法利用正交局部保持投影探索数据内部局部几何流形结构,对投影矩阵施加L2,0范数约束动态选择最优特征组合,采用嵌入锚点策略快速构建数据矩阵相似图,并设计了一个有效的迭代算法在避免引入正则化参数的情况下优化目标函数问题。通过在4个公开数据集上比较其他4种无监督特征选择方法,实验结果表明:FAFS算法选择了更优的特征,算法效率也得到了提升。
1 基于锚点策略的FAFS算法
1.1 FAFS目标函数
本文利用局部保持投影(LPP)[14]的数据空间结构保持思想,引入L2,0范数约束,通过结构化稀疏投影矩阵选择特征。为增强算法的线性映射能力,同时对投影矩阵施加单位正交约束,这对算法处理后的数据重构提供了便利。
若给定一个原始样本数据矩阵,X=[x1,x2,…,xn]∈d×n,W∈d×m为投影矩阵,Y=[y1,y2,…,yn]∈m×n为数据投影后的矩阵,且有Y=WTX。定义Tr(·)为矩阵的迹,‖·‖2,0为矩阵的L2,0范数,LPP算法解决如下问题
(1)
式中Sij为原始样本数据点xi和xj之间的相似度,是原始数据点之间距离的度量。该目标函数尽量保持数据点投影前后的距离关系,如果样本数据点xi和xj接近,那么投影后的yi和yj也接近,此时Sij很大,反之则Sij值很小。上述目标函数可以进一步推导
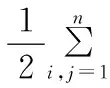
=WTXDXTW-WTXSXTW
=WTX(D-S)XTW=WTXLXTW
(2)

对投影矩阵施加单位正交约束,同时约束投影矩阵W的L2,0范数等于k,‖W‖2,0=k,这表示W矩阵只有k个非零行,对应的序号即为所选择的k个特征的索引。将目标函数用矩阵迹的形式表示为
min Tr(WTXLXTW),s.t.WTW=I,‖W‖2,0=k
(3)
目标函数中k值为预先设置的要选择的特征数目,投影矩阵W为需要优化求解的未知量。优化目标函数前提是求出L矩阵,L矩阵可以通过构造数据矩阵相似图来求得,所以接下来要先求解数据矩阵的相似度矩阵。
1.2 基于锚点策略的相似图学习
传统的构造数据矩阵相似图多采用谱分析法。基于谱分析的K近邻方法构造的相似度矩阵通常几乎是满秩的,这无疑会给算法带来巨大的时间和计算开销。另外,基于谱分析方法,采用高斯核函数来度量数据点之间的相似度也会引入带宽参数。而采用嵌入锚点的方法学习到的是样本数据的高度稀疏、对称且半正定的相似度矩阵。在基于锚点策略的图相似矩阵的构造中,首先要考虑的是如何生成锚点。基于锚点策略的方法通过从原始n个数据样本中找到p(p≪n)个锚点构建数据矩阵的相似图,然后计算数据点与其近邻的c个锚点之间的距离。数据点与锚点连接示意如图1所示。

图1 数据点与锚点连接示意
数据点与锚点是稀疏连接,最终得到的相似度矩阵也是高度稀疏的。本文使用K-means聚类方法生成标志性的锚点,定义G∈d×p为选定的锚点矩阵,Gi为第i个原始数据采样点的c个最近邻锚集。第i个样本数据点与其c个近邻锚之间的相似度计算满足如下模型问题

(5)用拉格朗日乘子法对式(5)进行求导得到拉格朗日函数为
(6)
式(6)优化求解的详细过程可以参见文献[15],最后求解结果为
(7)
锚点相似度矩阵的表达式只包含一个预先设置的整数近邻c参数,并且公式只涉及简单的运算,相似度值对应距离属性。原始样本数据的相似度矩阵可以在锚点相似度矩阵的结果基础上,按照Liu W等人[12]提出的方法设计,如下所示
(8)
式中Λ为对角矩阵,其对角元素为E矩阵的列和。此外,相似度矩阵S为一个稀疏对称、PSD且双随机矩阵,这些性质对于图的学习和提高算法的性能非常有用。
2 目标函数求解
2.1 模型优化
在优化目标函数问题时,由于目标函数中含有L2,0范数NP难问题求解比较困难,许多研究者往往做近似处理,转化为求解L2,1范数问题
min Tr (WTXLXTW)+λ‖W‖2,1,s.t.WTW=I
(9)
式(9)问题需要迭代优化,但值得注意的是目标函数中涉及的正则化参数很难调整。对于不同类型的数据,正则化参数的取值可能不固定,这会削弱模型的泛化能力。为避免参数调整问题,本文巧妙设计了一个迭代算法直接求解L2,0范数模型问题,并且不会引入正则化参数。首先对目标函数式(3)作一个等价变换
max Tr[WT(λI-XLXT)W],s.t.WTW=I,‖W‖2,0=k
(10)
式中λ的值为矩阵XLXT的最大特征值,变换目的是保证矩阵λI-XLXT半正定,这也是迭代算法需满足的前提条件。令H=λI-XLXT,目标函数简化为
max Tr[WTHW],s.t.WTW=I,‖W‖2,0=k
(11)
针对目标函数式(11),巧妙地设计了一个由原始矩阵近似的低秩代理协方差矩阵P,迭代更新并求解了一般的L2,0范数目标函数问题。利用低秩代理协方差矩阵P参与行选择矩阵的映射,并选取行选择矩阵的特定k行进行迭代更新,得到目标函数的最优投影矩阵W。迭代求解投影矩阵W的流程如算法1所示。
算法1迭代优化投影矩阵W
输入:样本数据矩阵X,选择的特征数k;
Step1:随机初始化一个投影矩阵W满足WTW=I;
Step2:计算矩阵P=HW(WTHW)-1WTH;
Step3:根据P的对角线元素选取最大的k个,其对应位置的k行序号为W非零行的位置,W其余行元素置0;
Step4:计算M=HW,取对应位置的k行元素组成∈k×m,用的任意一个标准正交基,来更新W对应位置的行,W其余的行为0;
Step5:迭代Step2-Step4直到收敛;
输出:投影矩阵W。
2.2 收敛性证明
针对模型优化迭代算法全局收敛性问题,下面给出两个引理进行证明。
引理1[16]:若A∈n×m,B∈n×m,并且n≤m,设λi(A)为n阶矩阵A的特征值(i=1,…,n),则有∀1≤i≤n︰λi(BA)=λi(AB),且有∀n+1≤i≤m︰λi(BA)=0。

定理1:对于算法中的Wt+1,有
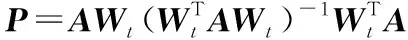
(12)
证明
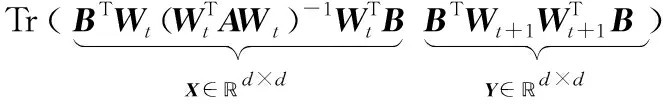
(13)
其中,第一个不等式来自Wt+1的定义;第二个不等式根据引理2;最后一个等式根据引理1,这是因为有
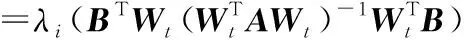
k+1≤i≤d︰λi(X)=0
(14)
证毕。算法中的迭代优化算法在每次迭代中单调增加问题(10)的目标函数值,直至收敛。
3 实验与分析
选取了4个公开的标准数据集实验,并用分类正确率(accuracy,ACC)和标准化互信息(normalized mutual information,NMI)2个指标与其他4种无监督特征选择算法进行了比较,评价和分析算法性能。记录算法运行时间,绘制目标函数值变化曲线,通过实验证明了算法的收敛性。
3.1 数据集
实验共选取了4个标准数据集:图像数据集COIL20,包含从20个物体的不同角度拍摄的1 440张照片;ORL面部数据集,它是40个人的10种不同表情拍摄的400张图像;显著性检测图像数据集MSRA25,它是MSRA图像数据集的子集;Palm25图像数据集,包含2 000幅手掌细节图像。表1具体描述了这4个数据集。

表1 数据集描述
3.2 评价指标
实验采用ACC和NMI指标对算法性能进行评估。定义yi为样本数据点xi自带的类别标签,fi为算法对样本数据点xi预测标签,ACC计算公式如式(15);定义矩阵P为算法聚类结果,矩阵Q为数据实际标签矩阵,NMI计算公式如式(16)
(15)
(16)
式中n为样本数目,δ(x,y)为比较函数,若x=y,则δ(x,y)=1,否则δ(x,y)=0;H(P)和H(Q)分别为P和Q的熵,I(P,Q)为P和Q之间的互信息。
3.3 对比算法
为了验证FAFS算法的性能,本文将其与LS[18]、MCFS[19]、UDFS[12]、SRCFS[20]4种无监督特征选择方法进行了比较,将使用所有特征Kmeans分类的结果作为基线(Baseline)。在实验中,所有算法的近邻数据点数目都设置为5。对于LS算法,需要调整高斯核函数的带宽参数;对于MCFS,UDFS算法,需要调整正则化参数。为保证比较实验的公平性,本次实验采用网格搜索法,从{10-3,10-2,10-1,1,101,102,103}中取值对参数进行调整。实验中FAFS算法锚点数量p根据实验经验选取数据集样本数量约25 %的整数。为减小K-means初始化对实验结果的影响,取10次实验的平均值作为算法的最终结果。
3.4 实验结果与分析
实验中所有算法选择不同特征数目的ACC和NMI值变化曲线分别绘制如图2和图3所示。
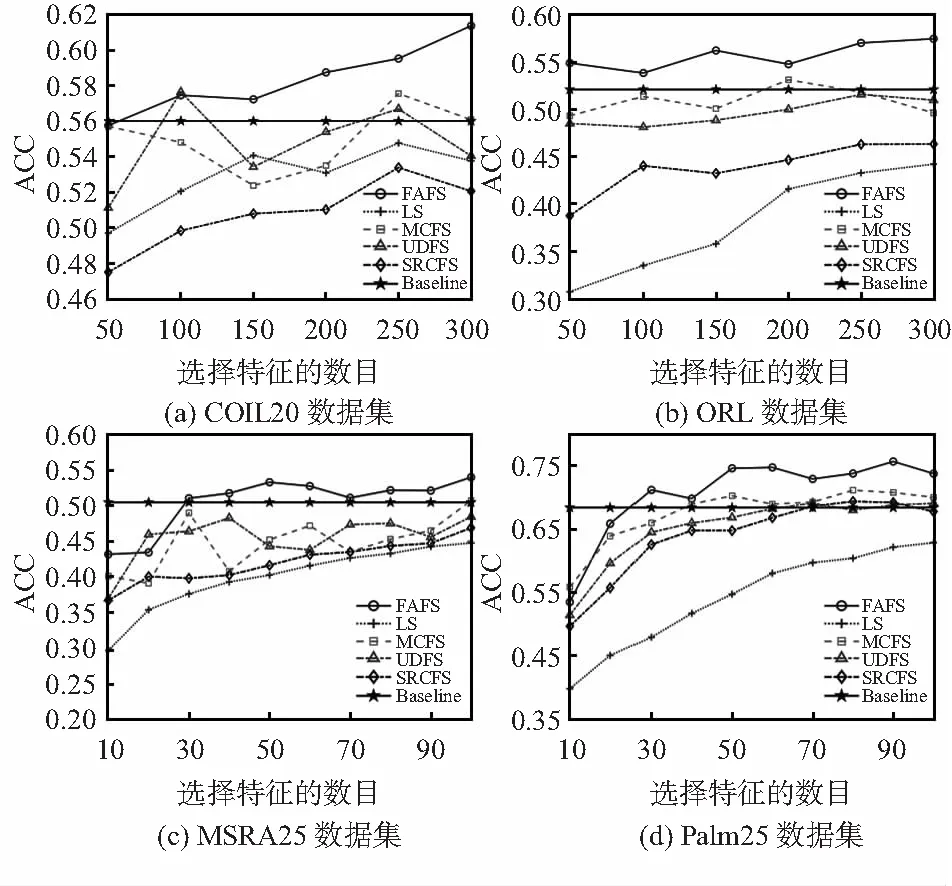
图2 数据集选择不同数量特征的聚类精度
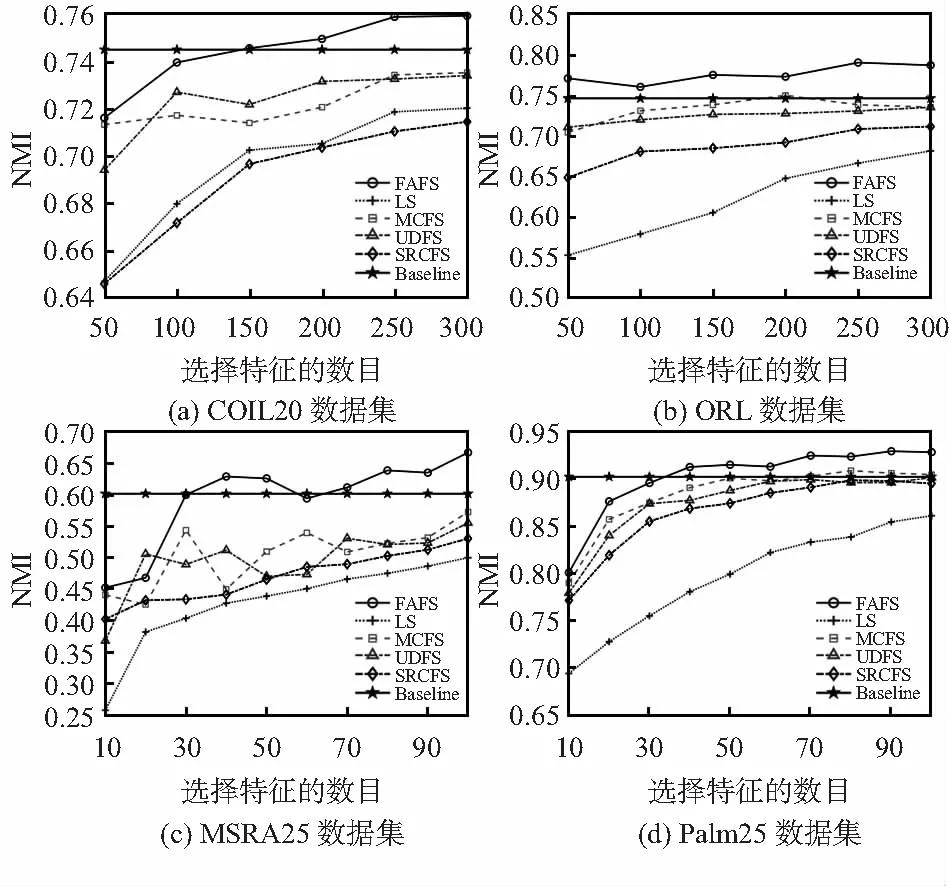
图3 数据集选择不同数量特征的NMI
从图2和图3中4个数据集ACC和NMI变化曲线可以看出,本文提出的FAFS算法总体性能优于所对比的算法,在COIL20,ORL和MSRA25数据集上的性能提升尤为显著。在ORL数据集上,与其他比较算法和基线相比,分类准确率提高了10 %左右,表明该算法对ORL中这类数据的所选特征更具代表性。图3中NMI结果也表明FAFS算法所选特征与数据的原始标签之间的相关性总体上也优于比较算法,这证明该算法提高了所选特征的质量。
另外,统计实验中选取最大数量特征时各算法的运行时间如表2。最后,绘制COIL20和MSRA25两个数据集的目标函数值变化曲线如图4。

表2 各算法在数据集上运行时间
在算法运行时间方面,表2标出运行时间最短的前两位。从表中可以看出,FAFS算法速度大体上仅次于LS方法,表明基于锚点策略的构图方法对于算法运行效率提升显著。LS方法虽然时间最短,但它只对数据特征的拉普拉斯特征分数进行简单的排序,算法实际性能在所有对比算法中最差。从图4中目标函数值的变化曲线可以看出,FAFS算法在前10次迭代内目标函数值上升非常快,随后减缓并趋于平稳并逐渐接近收敛,验证了算法的收敛性。

图4 数据集在算法1的变化曲线
4 结束语
本文针对稀疏正则化模型提出了FAFS算法。在原始数据点中嵌入锚点快速构建相似图,通过对投影矩阵施加L2,0范数约束来选择特征,将局部结构学习和特征选择融为一体。算法不需要复杂的调参步骤就能有效选择特征,在后续的公开数据集对比实验中表明算法性能优于其他几种对比算法,尤其在算法运行速度上得到了显著改善。

