高炉渣液滴破碎过程数值模拟

杜宇航，刘晓宏，温 治，楼国锋

（北京科技大学 能源与环境工程学院，北京 100083）

高温熔融高炉渣是钢铁行业主要的副产品之一，具有热量高，产量大等特点，因此回收利用高炉渣有着重要的现实意义和经济意义［1-2］.气淬粒化是一种高炉渣粒化工艺，核心原理是利用高速气体与熔融高炉渣之间的碰撞、剪切和摩擦作用生成微小颗粒.气淬粒化过程极其复杂：熔融渣液柱在与气流接触后会形成大量液滴、液丝及不规则液体团块，这一过程为初次破碎；而后这些液体结构又会在后续气流的强烈作用下进一步破碎形成更小的液滴，这一过程为二次破碎［3］.经初次破碎生成的高炉渣液滴在后续流场中能否发生二次破碎，主要由韦伯数（We）决定.目前，液滴二次破碎的研究对象主要是水和液态燃料，很少有涉及类似高炉渣液滴的高温熔体.因此，本文中对高炉渣液滴破碎过程进行数值研究，获得其发生破碎的临界We，用以指导气淬工艺流场布置.

围绕一般性液滴的变形和破碎，国内外已经做了大量的研究，并取得了重要的研究成果.大量实验研究表明，液滴破碎主要受韦伯数（We）、奥内佐格数（Oh）、雷诺数（Re）、密度比和黏度比等无量纲参数影响，其中We和Oh影响较大［4］.Hsiang和Faeth［5］、Pilch和Erdman［6］均发现在低Oh下，液滴破碎过程随着We的增大呈现出不同的破碎形态，这些形态可分为振动破碎、袋状破碎、多模态破碎、剪切破碎和灾难破碎.根据目前研究表明［7］，在Oh远小于0.1的条件下，液滴破碎的临界We为11±2，而对于Oh＞0.1的高炉渣液滴，破碎的临界We尚不明确.

在数值模拟方面，张文英等［8］使用VOF法研究了不同We条件下大水滴的袋状破碎形态；张志荣等［9］通过计算获得低温低速烟气中液滴破碎的临界We为10.6，并发现Re不是破碎的关键因素；樊玉光等［10］具体研究了液化天然气液滴的破碎过程.以上数值模拟研究均未考虑温度对破碎过程的影响，但熔融高炉渣的温度极高，破碎时的传热作用很有可能会引起凝固现象，从而对破碎过程产生一定影响.因此，对破碎过程进行传热分析是十分必要的.

为弥补以上研究的不足，本文中将VOF模型、RNGk-ε湍流模型和凝固／熔化模型相结合，对空气作用下的高炉渣液滴破碎过程进行二维数值模拟，定性评价高炉渣液滴破碎的形态变化，分析传热过程对破碎过程的影响，并进一步探究不同Oh条件下发生破碎的临界We，以期为气淬工艺流场参数研究奠定基础.

1 数值方法建立及验证

高炉渣液滴的破碎过程极其复杂，因此对模型做出以下假设：①流场模型为二维轴对称模型，高炉渣液滴的初始形状为球形；②气液两相均为不可压缩流体；③液滴的初始温度为1 773.15 K，空气的初始温度为300 K；④忽略辐射过程.本文中使用VOF模型实现液滴界面追踪，流场中的湍流选用RNGk-ε模型.同时，由于破碎过程中可能发生凝固现象，在原模型基础上添加凝固／熔化模型.

1.1 控制方程

本文的研究对象是球形静止高温高炉渣液滴，主要的控制方程如下：

质量守恒方程：

动量守恒方程：

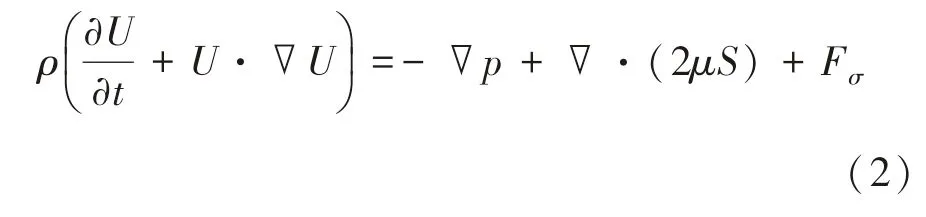
式中：U为流体速度矢量，m／s；p为压强，Pa；S为黏性应力张量，s-1，Si，j＝（∂iuj＋∂jui）／2；ρ为流体密度，kg／m3；μ为流体动力黏度，kg／（m·s）；Fσ为表面张力矢量，N／m3.VOF模型定义了参数α，表征网格中液体的体积分数，并假设：α＝0为气相；0＜α＜1为气液界面；α＞1为液相.

通过对相分数的追踪来确定两相界面，而相分数α通过相分数方程计算：

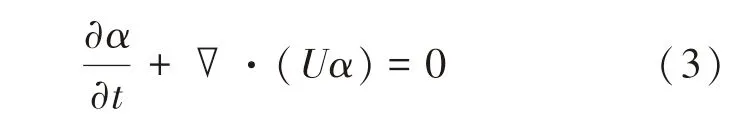
网格内物性参数计算式如下：

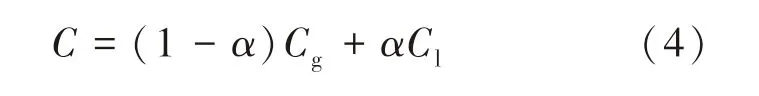
式中：C表示密度、动力黏度、比热容、导热系数等参数；下标l表示液相；下标g表示气相.

对于式（2）中的表面张力矢量Fσ，使用Brackbill等［11］提出的连续表面力模型（CSF），计算式如下：

式中：σ为表面张力系数，N／m；κ为界面曲率；ρ为混合相的密度，kg／m3，可利用式（4）计算.

本文中采用热焓-多孔介质法处理高炉渣传热和凝固计算，传热控制方程为

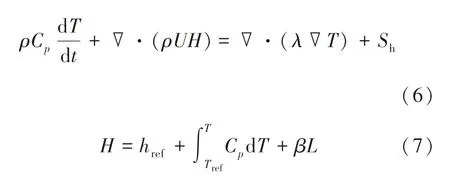
式中：Sh为热源项，J／（m3·s）；Cp为比热容，J／（kg·K）；λ为导热系数，W／（m·K）；L为凝固潜热，J／kg；href为相对于Tref的参考热焓，J／（kg·mol）；β为单元内的液相分数.

1.2 计算模型

数值模拟使用的几何模型如图1所示.流场大小为15 mm×60 mm，底边为轴对称边界，左侧为空气入口，设为速度入口边界条件（速度为Ug），右侧为自由出流边界条件，而上侧边界为对称边界条件.其中，直径为D的静止高炉渣液滴置于距离入口6 mm的位置，然后在空气的冲击作用下运动.本文中使用商业软件ANSYS FLUENT v201模拟高炉渣液滴的破碎过程.

图1 计算模型示意图Fig.1 Schematic of computing model

1.3 物性参数设置

采用某公司高炉渣的部分物性参数作为模拟参数（如黏度和密度），其余参数采用文献［11-13］的数据.其具体成分见表1.

表1 高炉渣成分表（质量分数）Table 1 Composition of blast furnace slag（mass fraction） %

考虑到高炉渣液滴的主要热物性参数随温度变化对破碎过程的影响，高炉渣液滴的导热系数λ随温度变化的表达式为［11］

高炉渣比热Cp随温度变化的表达式为［12］

对高炉渣黏度测量并拟合，可得到高炉渣动力黏度μl随温度变化的表达式为

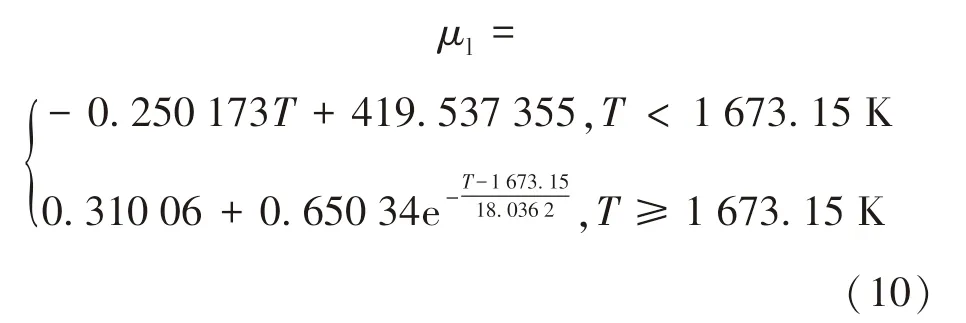
计算中使用的高炉渣其他物性参数见表2.高炉渣是由多种物质组成的混合物，熔点非固定值.熔融温度是指高炉渣完全成为液相时的温度或液相态高炉渣冷却后开始析出固相物的温度；凝固温度是指高炉渣完全成为固相时的温度或固相态高炉渣开始熔融形成液态的温度.

表2 高炉渣其他物性参数［13］Table 2 Other physical parameters of blast furnace slag

1.4 网格无关性分析

网格对VOF模型的模拟结果影响很大，因此如何在保证计算精度的前提下降低计算成本是需要考虑的问题.图2示出了不同网格分辨率下D为3 mm的高炉渣液滴在空气流中形态的演变过程（网格分辨率D／h为60，75和100，D为液滴初始粒径，h为网格尺寸）.从图中可以看出：在变形初期，三种分辨率的液滴形状基本重合；随着变形的加剧，低分辨率液滴开始偏离中高分辨率；当时间为10 ms时，中高分辨率液滴已破碎，但低分辨率液滴还未破碎，这说明分辨率为75的网格已能够捕捉液滴的破碎过程.因此本文中后续模拟均使用D／h＝75的分辨率进行计算.

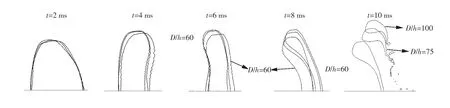
图2 不同网格分辨率下高炉渣液滴形态演化Fig.2 Evolutions of slag droplet shape under various mesh resolution

2 数值计算结果分析

2.1 高炉渣液滴破碎形态分析

图3示出了初始温度1 773 K、空气流速47 m／s、粒径3 mm的高炉渣液滴变形破碎过程.从图中可以看出，高炉渣液滴破碎过程可分为4个阶段：①初始变形阶段［图3（a）～（c）］，液滴进入气流后，匀速流场迅速变为绕流流场，在液滴迎风侧形成驻点和高压区，导致液滴的迎风端被挤压变平；②延伸发展阶段［图3（c）～（h）］，在气动力的持续作用下，液滴整体被挤压变平，形成圆饼形液滴；③袋状结构形成阶段［图3（h）～（m）］，气流驻点的高压区不断被挤压，致使中心部分液体由赤道位置向极点位置运动，液滴从厚度均匀的饼状结构向边缘厚中间薄的袋状结构发展；④袋状破碎阶段［图3（m）～（n）］，高压作用使袋状结构中间部位不断变薄，当薄到一定程度后，瑞利-泰勒（R-T）不稳定性会在其表面产生压力波动，这些波动形成的扰动会迅速在表面发展，幅度也会越来越大，最终穿透液滴形成孔洞并迅速扩大，导致中间多部位断裂与液环分离.

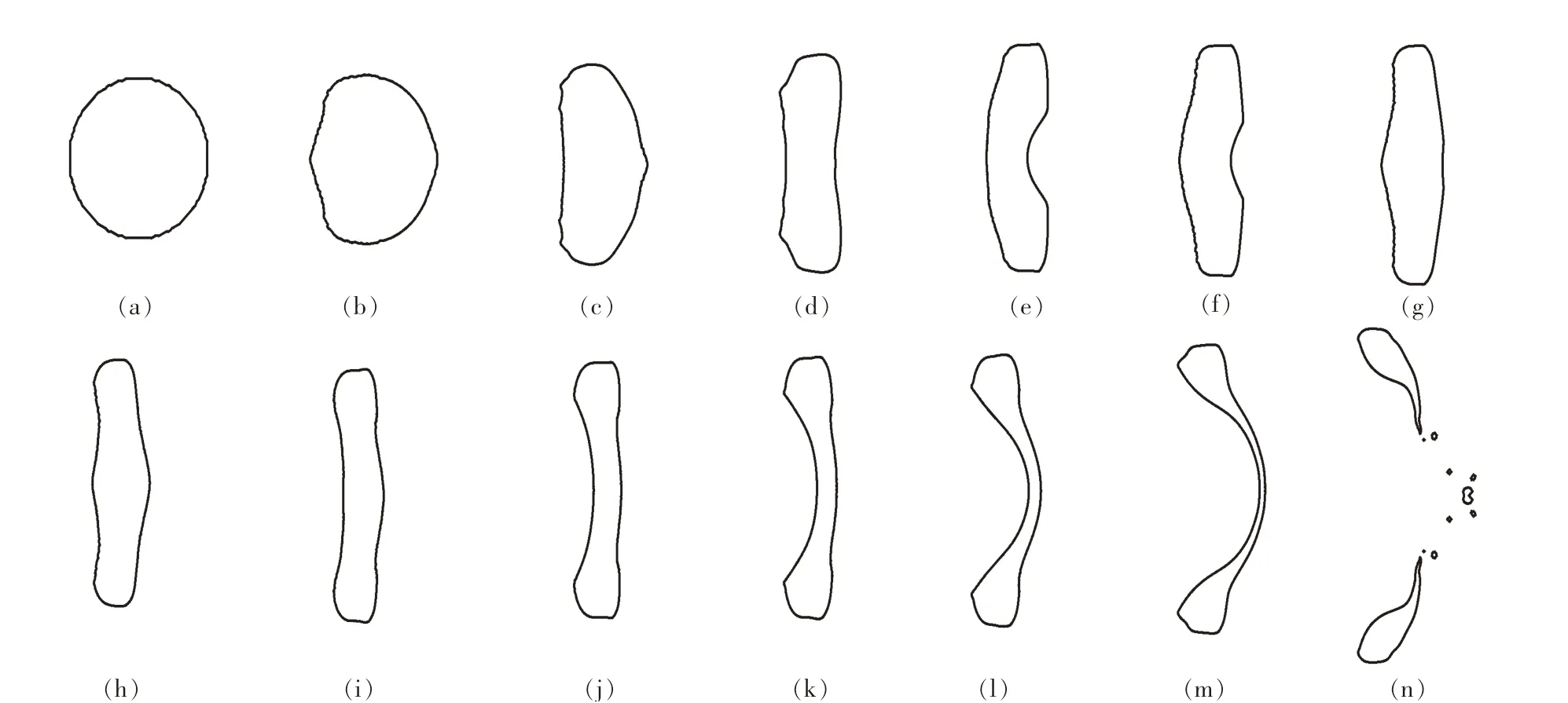
图3 U g＝47 m／s时高炉渣液滴随时间变形破碎过程（各图时间间隔1 ms）Fig.3 Deformation and breakup of molten slag droplet with U g＝47 m／s（time interval is 1 ms）

高炉渣液滴变形破碎是气动力、表面张力和黏性力共同作用的结果.气动力可促进液滴破碎，而表面张力和黏性力则会阻碍液滴破碎.在初始阶段，液滴内部相对静止，黏性力几乎为0，而在气体作用下非均匀分布的气动力会打破液滴内部的力平衡进而使其发生形变，这一过程同时也会引发各种力的变化.首先，形变会使液滴在气流方向上的面积增大，导致气动力增加，从而进一步促进液滴变形；其次，形变会使液滴内部发生轻微流动，形成黏性力，反而阻碍其变形；最后，液滴局部的曲率变化会导致表面张力变化，尤其是在形成圆饼形结构后，液滴两侧接近平面的表面张力大大减小，而上下两侧液环面的表面张力大幅增加，在不等表面张力作用下阻碍其进一步变形.

2.2 传热过程对高炉渣破碎的影响

图4 （a）为t＝12 ms时高炉渣液滴内部温度场分布图.从图中可以看出，此时液滴内部温度略有下降，且中心袋状结构处的高炉渣温度下降最多，下降了约36 K，而两侧液环温度仅下降了25 K.主要原因是随着液滴袋式结构的生成，中心部分的表面积增大，整体厚度降低，热量更容易往外传递.但无论在哪个区域，高炉渣的温度都没有降至凝固温度以下，说明此时液滴没有发生凝固，从图4（b）的液相分数场中也可以看出液滴内部均处于液态.

图4（c）为高炉渣液滴的动力黏度场分布图.从图中可以看出，破碎过程中不同区域的高炉渣黏度不同，袋式结构中心区域的动力黏度大于两侧液环区域，这是由于中心温度高于两侧.高炉渣的黏度与温度密切相关，当温度处于较高水平时，其黏度会随着温度降低缓慢增加，而当温度下降至临界黏度温度TCV时，黏度值会爆发式增大.从温度云图中看出，各点温度均大于临界黏度温度，因此液滴的整体黏度变化不大.

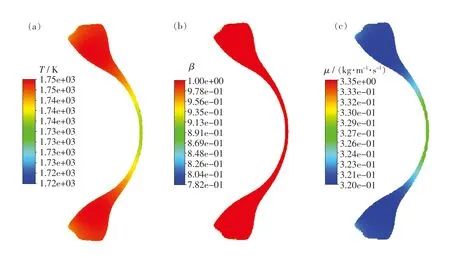
图4 t＝12 ms时高炉渣内部不同参数云图Fig.4 Different contours of blast furnace slag when t＝12 ms

综合以上分析可知，由于传热过程极为缓慢，高炉渣液滴破碎过程中的物性参数变化幅度小，从而对整个破碎过程影响较小.

图5示出了考虑与不考虑传热的破碎过程结果比较.从图中可以看出，两者破碎形态和破碎时间基本相同.由此说明，液滴破碎时间尺度远小于传热凝固时间尺度，高炉渣传热过程对破碎过程的影响极小.

图5 不同模型高炉渣液滴破碎过程Fig.5 The breakup of blast furnace slag droplet

2.3 高炉渣液滴破碎临界韦伯数

为了提高模拟效率，本文中忽略了破碎过程中的传热过程.假设高炉渣的黏度始终保持在初始温度1 773 K时的0.312 6 Pa·s.依据工业要求，高炉渣颗粒粒径至少要小于3 mm，因此本文选取粒径为3 mm的液滴.

研究表明，We和Oh对液滴破碎过程有重要影响，定义式分别为是气动力和表面张力的相对大小，而Oh则是黏性力和表面张力的相对大小.气动力能促进液滴破碎，而表面张力和黏性力则会抑制液滴破碎，液滴能否破碎以及其破碎模式均由这三种力之间的竞争关系决定.

2.3.1 初始粒径D对高炉渣液滴破碎形态的影响

根据We的定义，其大小与液滴初始粒径D和气流速度Ug有关.当空气的Ug不变时，D越大，We越大.图6示出了Ug为45 m／s时不同粒径高炉渣液滴的破碎过程.由图可知，当Ug保持不变时，随着D的增大，液滴的破碎模式会发生转变.当粒径为3 mm时，液滴在形成饼状结构后就基本保持形状不变；而当粒径达到3.1 mm及以上后，液滴在形成饼状结构后会迅速发展成袋状结构并破碎.在均发生袋式破碎的情况下，液滴粒径越大，生成的袋状结构越大，破碎生成的细小液滴越多，破碎效果越明显.

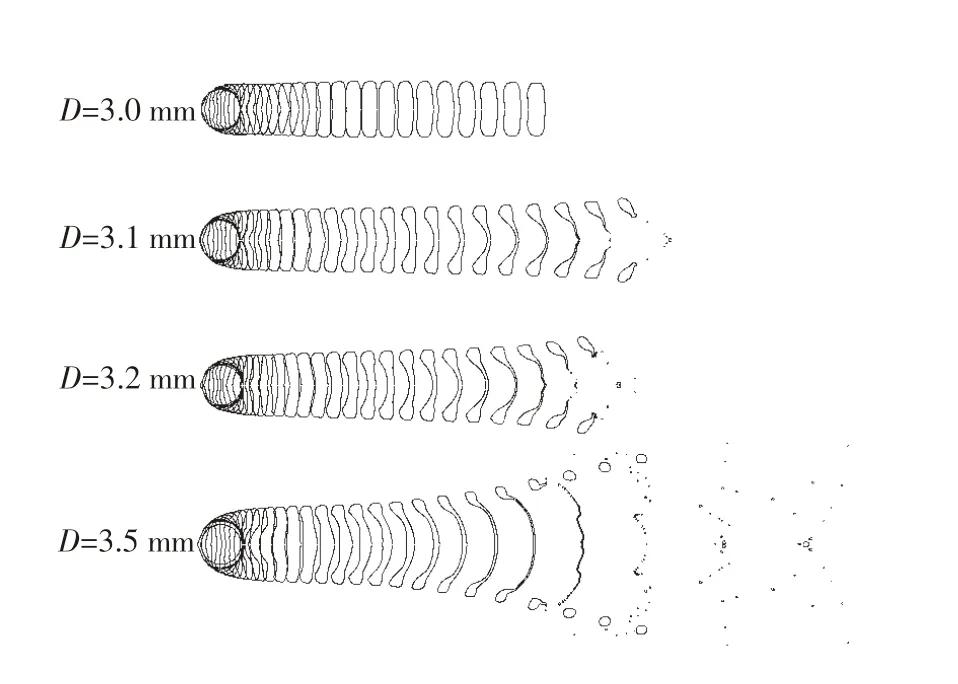
图6 不同粒径的高炉渣液滴形态变化（U g＝45 m／s，μl＝0.312 6 Pa·s）Fig.6 Slag droplet morphologies with different diameter（U g＝45 m／s，μl＝0.312 6 Pa·s）

液滴破碎模式发生改变的原因有两点：一是随着初始液滴粒径的增大，气流方向上的投影面积会增大，这导致液滴受气流的气动力增加；二是初始粒径的增大会减小表面曲率，从而减少液滴表面张力.气动力和表面张力的变化趋势均有利于液滴破碎，因此液滴粒径越大，发生破碎的可能性越大.

2.3.2 气流速度Ug对高炉渣液滴破碎形态的影响

当D一定时，We随着Ug增大而增大，而Oh不会改变，为了得到一定Oh下袋式破碎的临界We，只要增大Ug即可.图7示出了Ug分别为45，45.5，46和47 m／s时D为3 mm的高炉渣液滴破碎过程.由图可知，随着Ug的增大，破碎模式发生转变，且Ug越大，液滴越容易破碎.

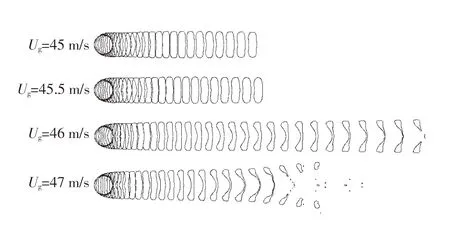
图7 不同气流速度下高炉渣液滴形态变化（D＝3 mm，μl＝0.312 6 Pa·s）Fig.7 Slag droplet morphologies with different gas velocies（D＝3 mm，μl＝0.312 6 Pa·s）

从图中可以看出，高炉渣液滴在速度低于45.5 m／s的气流作用下不会发生破碎，此时一般认为是振动破碎模式.振动破碎模式只发生在气流不稳定且液滴具有一定振荡频率时，生成的子液滴与母液滴的粒径相当.此外，振动破碎模式发生破碎需要很长时间，因此数值模拟很难计算到破碎时刻，在这种情况下默认未破碎即为振动破碎模式.

当Ug增大到46 m／s时，气动力开始超过表面张力和黏性力的阻碍作用，破碎模式发生转变，进入袋状破碎模式.但此速度下破碎前的袋状结构较小，袋状膜中心部分生成的细小液滴数量较少，大部分还在液环两侧.而当Ug继续增大到47 m／s时，可清晰观察到较大袋状结构的破碎过程，且破碎后生成许多小液滴.当Ug为46 m／s时，液滴处于刚刚达到袋状破碎的条件，因此得到初始温度为1 773 K的高炉渣液滴破碎的临界We约为15.5.

2.4 Oh对袋式破碎临界We的影响

高炉渣液滴的黏性力是阻碍变形破碎的主要因素之一，它会不断消耗气动力提供给液滴的能量.不同黏度的液滴破碎所需的气动力不同，黏度越大，破碎所需的气动力也越大.因此当黏度发生变化时，破碎临界We也会变化.本文中计算并分析了黏度为0.3126，0.4746，0.6365和0.960 4 Pa·s时不同气流速度下高炉渣液滴的破碎过程.

通过归一化处理，将不同Oh下不同We的破碎结果绘制成图，并与Gelfand，Cohen和Brodkey等［14-16］的实验拟合数据及Zhao［17］理论预测数据进行对比，结果如图8所示.由此还得到不同Oh下的破碎临界We／We0（其中We0为Oh趋于0时的临界We），如表3所列.从图8和表3可以看出，随着Oh的增大，破碎临界We也不断增大.由此可见，高炉渣黏性力越大，液滴越难破碎.该结论也从侧面反映温度对破碎的影响：在保持高炉渣熔融状态的温度水平下，温度越低，黏度越大.这意味着高炉渣初始温度越低，越难以发生二次破碎.因此，为了在高炉渣气淬过程中得到更小的粒径分布，应尽可能保证初次破碎生成的液体结构在高温水平上.

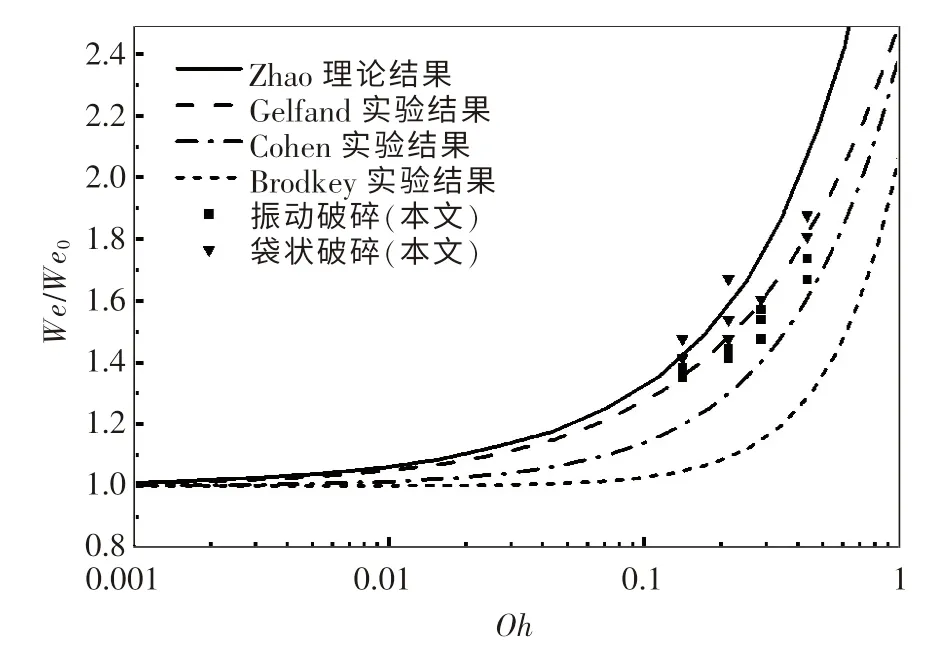
图8 不同Oh下破碎结果Fig.8 The breakup results under various Oh

表3 不同Oh下袋式破碎临界We／We0Table 3 Critical We／We0 of bag breakup under various Oh

Cohen等［15］认为在液滴没有黏性力作用的情况下，气流输送给液滴的动能等于表面能，再通过增加额外的能量项来等效液滴黏性力的影响，从而给出Oh与We之间的理论关系式为

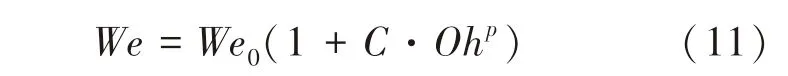
式中：C理论上为1～1.8；We0默认为11.

利用式（11）对表3数据进行拟合，拟合式如下所示：

3 结 论

（1）高炉渣液滴袋式破碎过程和其他液滴破碎过程一致，其变形由迎风面和背风面之间的压差导致，最终破碎主要由R-T不稳定性产生的压力扰动所致.

（2）由于高炉渣液滴破碎过程时间尺度远小于传热凝固时间尺度，高炉渣液滴的传热过程在破碎中并不关键，对整个过程影响极小.因此，模拟破碎过程可忽略传热过程的影响.

（3）液滴的初始粒径D和气流速度Ug是影响高炉渣液滴破碎的重要因素.随着初始粒径的增大，气流速度增加，液滴越容易发生破碎，同时破碎时间也会减少.

（4）在初始温度为1 773 K时，本文模拟研究的高炉渣发生破碎的临界We为15.5.

（5）高炉渣液滴破碎临界We随黏度的增加而增大，本文模拟研究的高炉渣Oh在0.1到0.45之间，临界We随Oh变化的拟合式为We＝We0（1＋1.204 91Oh0.57591）.