基于半定松弛优化估计的无线传感网络定位

李晓飞，陈广福，蓝天明

（1.茶产业大数据应用与智能化重点实验室，福建 武夷山 354300；2.武夷学院数学与计算机学院，福建 武夷山 354300）

无线定位在过去几十年吸引了大量学者关注，是无线传感器不可或缺的最重要组成部分。当这些无线传感器节点的信号能被确认地理位置时，这些信号数据才具有意义。基于能量的无线定位利用接收信号强度(RSS)将传统定位技术，如TOA[1−2]、TDOA[3−4]和AOA[5]，变成简单的定位计算。近年来，基于精度分析的定位在各种网络中均有应用，包括无线传感器网络(WSNs)[6]、无线局域网(WLAN) [7]和车载自组网(VANETs)。基于接收信号强度的定位算法会导致非线性和非凸优化问题。为了解决这个问题，文献[8]提出了一种加权最小二乘算法（WLS），近似估计传感器节点位置以及采样变换的发射功率。文献[9]首先对低噪声水平的ML 算法进行近似估计，然后将基于二阶锥规划（SOCP）的凸优化算法应用到ML 估计的松弛方法中。针对基于接收信号强度（RSS）的定位问题，文献[10]设计了半定规划算法。传统的无线传感器网络定位算法设计是基于经典的信道路径损耗模型，噪声为高斯分布。由于噪声的非均匀性以及多源性，噪声并不总是服从高斯分布[11]，因此，传统的高斯模型不能很好地表示测量到的噪声，导致定位算法的错误。众所周知，至今还没有研究无线传感器网络节点算法中基于非高斯噪声模型的实际信道路径损失模型。为此，本文提出一种基于无迹卡尔曼滤波[12]的半定松弛优化估计算法（SCSDP 算法），以实现无线传感器网络中节点位置的准确估计，噪声由非高斯模型表示，然后对噪声进行经验参数估计。同时，本文将定位作为一个优化问题来实现半定松弛化，并对后续的非线性和非凸优化问题求解，得到次优解。实验结果表明，本文提出的半定松弛优化估计（SC-SDP）算法性能优于传统定位算法。本文的具体贡献如下。

1) 本文提出一种基于半定松弛优化估计算法的定位技术，建立系统模型并将其作为一个优化问题，通过寻找初始非凸目标函数的更低下界来重新阐述优化问题，将非线性和非凸问题分别松弛优化，得到次优化解 。

2) 本文采用无迹卡尔曼算法过滤噪声，获得了一个可更准确地捕捉真实均值和协方差的滤波器，采用无轨迹转换使高斯输入信号精确到三阶，非高斯输入信号精确到二阶。这不仅避免噪声产生干扰，增加了系统的抗干扰性，而且提高了SC-SDP 算法的定位精度。

3) 通过大量的实验分析，其结果表明SC-SDP算法在无线传感器网络的定位误差（RMSE）要优于GM-SDP[13]、WLS[8]以及CRLB[13]的定位误差，其精度比其他算法要高。

1 系统模型和初步探究

假定第j目标节点未知坐标为θj=[θj1,θj2]T(θj∈R2，j=1,2,···,M)，第i参照节点αi=[αi1,αi2]T(αi∈R2,i=1,2,···,N)，其中M和N分别是目标节点和参考节点的总数。从第i个参考节点接收的第j个目标节点功率建模为

式中：P0是接收机在参考距离d0的传动功率；d(θj,αi)=||θj−αi||2是第j目标节点和第i参照节点之间的距离；γ是2 和6 之间的路径损失指数；附加噪声 ηi,j服从高斯分布，分别表示多路径环境中的对数正态投影效果。

高斯混合的噪声模型及观测功率矢量Pj=[Pi,j,Pi+1,j,···,PN,j]，所产生的第j目标节点的联合条件概率为

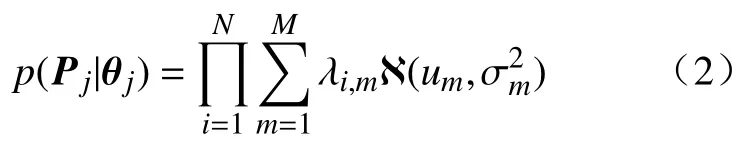
式中：λi,m是噪声的均值um和方差的簇m相应的权重；M是混合组件的数量。

2 问题的提出及解决方案

其中，Ψ(θj,λ)是联合条件概率密度函数的对数似然函数，Ψ(θj,λ)=lnp(Pj|λj)，同时混合权重 λi,m的总和等于1。然而目标函数的组合属性导致NP 难问题[14]。为了降低优化问题的复杂性，可以通过寻找初始非凸目标函数的更低下界来重新阐述优化问题。然后，通过松弛法重新阐述问题，作为SDP 问题求解，得到全局最优解。

对可行性的配对(θj,λ)，如果该对是公式（4）优化问题的最优解，为：

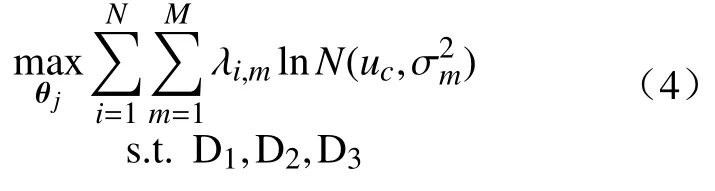
那么，配对(θj,λ)是公式（3）优化问题的次优化。

采用Jensen 不等式，公式（5）为公式（3）的初始非凸加权目标函数的下界，为

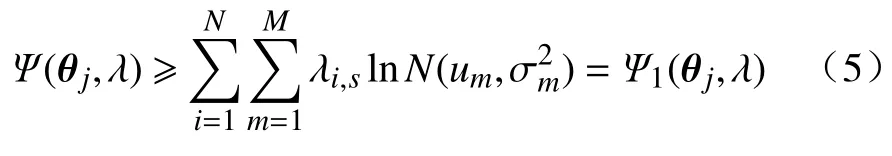
Ψ1(θj,λ)是参数(θj,λ)的对数似然函数的更低界。∃ω′，ω′使参数(θj,λ)满足Ψ1(θj,λ)≥Ψ∗−ω′。

公式（3）优化问题可以重新阐述为：

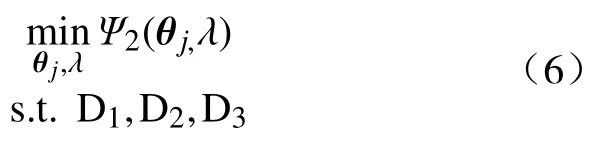
其中，

将公式（6）重新改写成公式（8），为：

公式（9）是凸优化问题，可以利用现存的工具解决初始优化问题公式（3）的全局优化方案。

3 半定松弛优化估计的去噪算法

本文采用的去噪算法是无迹卡尔曼滤波（UKF）算法。如同KF 算法[15]和EKF 算法[16]，UKF 算法还利用了预测校正周期。EKF 算法通过简单地执行一阶非线性函数的线性化变换来近似非线性系统的状态，而UKF 算法通过使用确定性抽样方法解决了这个问题 。这种采样技术主要选取均值周围样本点集最小值集合。它在预测器和校正器之外还有一个额外的步骤，即选择2×n+1 个sigma点。这些sigma 点传播到非线性系统，并从估计的均值和协方差恢复。该算法能得到一个更准确地捕捉真实均值和协方差的滤波器，无轨迹转换的使用能精确到高斯输入信号的三阶近似，非高斯输入至少为二阶。假定先验状态及误差协方差 δt可以表示为：

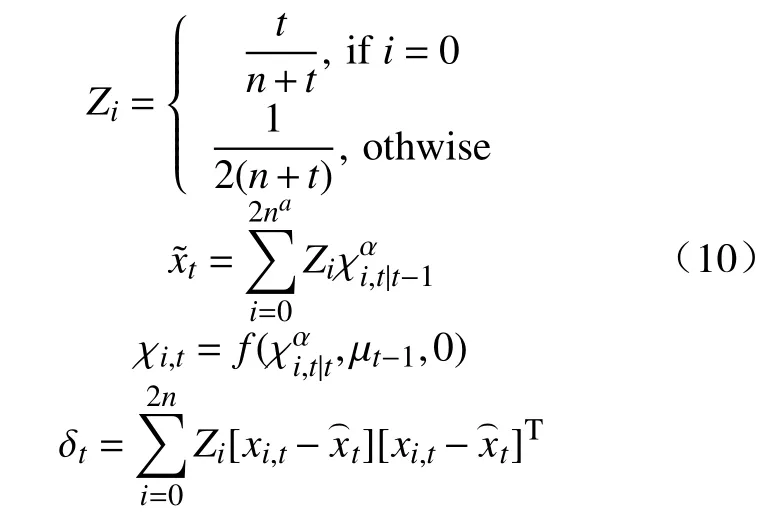
而校正阶段可以表示为：

4 半定松弛优化估计（SC-SDP）算法的伪代码

Step1，输入i参照节点和j节点目标节点的坐标。

Step2，计算功率建模为

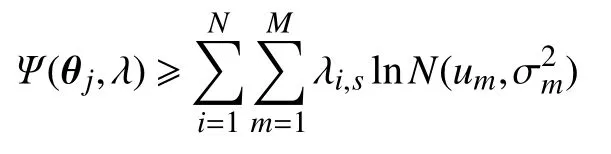
Step4，∃ ω′，ω′使参数(θj,λ)满足Ψ1(θj,λ)≥Ψ∗−ω′。

公式（3）优化问题可以重新阐述为：

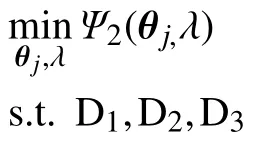
Step5，为了解决凸优化问题，利用现存的工具解决初始优化问题公式（3）的全局优化方案，为

Step6，利用无迹卡尔曼滤波（UKF）算法，通过使用确定性抽样方法解决去噪问题。

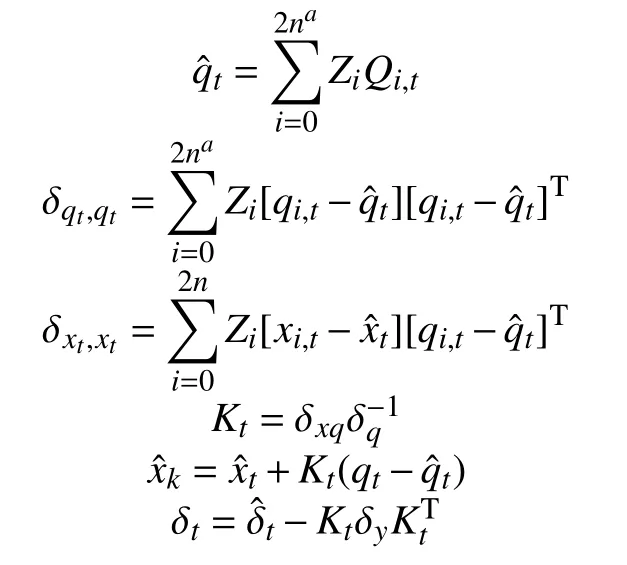
Step7，选择2×n+1 个 sigma 点，将这些sigma点传播到非线性系统，获取一个能更准确地捕捉真实均值和协方差的滤波器，以去除噪声。

5 实验结果与分析

5.1 编码相位转移的传统估计

传感器执行的核心操作之一是估计局部和输入扩展编码，也是基于编码的交叉关联函数的评估。交叉关联函数依赖于传播编码的特性。考虑传感接收器的信号数据采集到的局部编码[17]，为

式中：βi={1−11−1−1−1−11−1−1−11−1−1111−1}；r(t)是单位幅度矩形函数；Tc是芯片的宽度；编码频率Rc=0.5 MHz。假定dloc(t)是周期性的输入信号，可以评估交叉关联函数的属性。伪随机噪声序列的交叉关联函数的属性之一是当2 个编码完全相对应时具有一个最大值，即dloc(t)是din(t)的不确定时间。根据要求的样品率，取伪随机噪声序列样品之后，关联函数由公式（2）得出，为

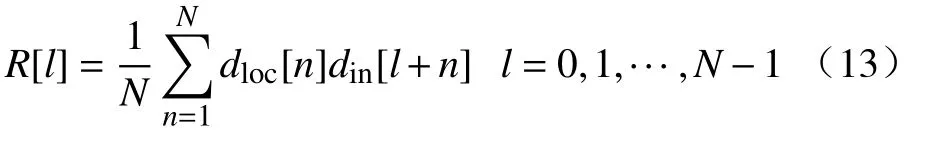
关联函数运行的结果如图1 所示，表示0 级芯片延迟时呈现的最大值情况，假定样品频率为10 MHz。

图1 0 级芯片延时Fig.1 0 chip delay

当输入信号的初始编码级跳转到4 级芯片时，最大4 级延时的交叉关联函数的运行结果如图2所示。

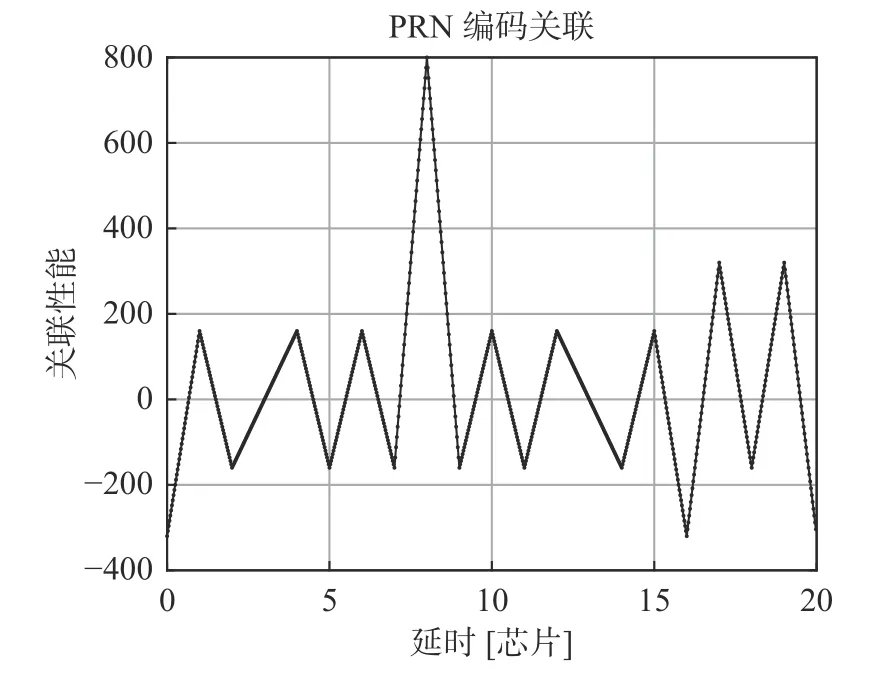
图2 4 级芯片延迟时间Fig.2 Fourth chip delay

当2 个编码完全对应的时候，伪噪声序列PRN的自动相关联函数拥有4 级芯片延迟的最大值。考虑高斯白噪声的因素，接收函数s[n]可改写为

式中：cin[n]表示输入信号的样品；w[n]表示白噪声；N为样品总数。

最大编码相位值G，为

式中：Rc表示白噪声的编码频率；fs表示输入信号的白噪声相关联函数。由公式(15)可知，当噪声标准方差值达到2.5，输入信号的白噪声相关联函数fs的最大编码相位值G是3.99，而实际的最大编码相位G是4。若噪声标准方差等于12，在2 个传播编码之间的关联函数最大编码被噪声干扰，信号取值导致编码相位转移出现偏差。

5.2 半定松弛优化估计算法的实验结果分析

本文采用若干个实验评估半定松弛优化算法性能并对实验结果进行分析。如图3，考虑100×100 m2的二维正方形区域，独立部署240 个传感器，包括20 锚。假定噪声遵从双模高斯混合分布，α1=0.67，β1=−4.36 dBm，σ1=6.83 dBm，α2=0.84，β2=3.76 dBm，σ2=5.63 dBm。室内噪声检测技术就是计算每混合组件的均值和方差值。本文采用100 个蒙特卡洛自带的20 个不等锚定量计算RMSE的值来评估室内噪声水平。

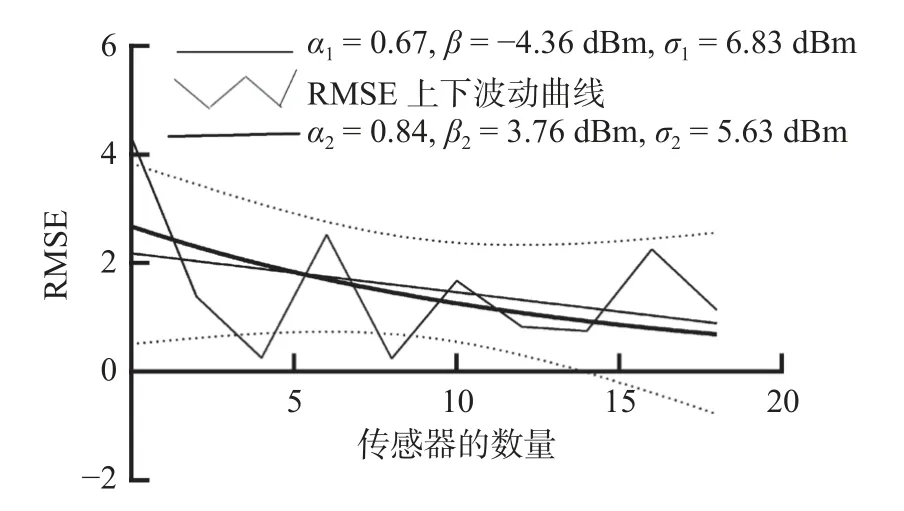
图3 传感器数量和 RMSE 的关系Fig.3 Relationship between the number of sensors and RMSE

由图3 可知，随着传感器数量的增加，噪声的干扰也越来越影响到无线传感器网络的性能。随着传感器数量的增加，均方根误差（RMSE）随着方差的变化出现向下波动。当噪声方差σ1=6.83 dBm时，传感器数量的增多，导致更多噪声干扰以及信号传输的不稳定，均方根误差(RMSE)向下波动增大，当再加入噪声方差σ2=5.63 dBm时，2 个噪声叠加在一起形成双模高斯噪声，随着传感器数量增加，更多噪声干扰导致均方根误差(RMSE)向上波动增大。

5.2.1 均方根方差（RMSE）的实验分析

本节分析了半定松弛化定位问题的实验结果。假定有N个参考节点均匀分布在以（0,0）为圆心，200 m 为半径的圆周上。第i参考点（i=1,2,···,N）的位置为

将本文SC-SDP 算法与半定规划算法SDP[18−19]、ML 算法[20]进行比较，并以CRLB 算法作为无线传感器网络定位性能的比较标准。利用凸优化（CVX）[21]解决半定松弛优化估计（SC-SDP）算法。基点和参考点不同的几何层次影响了定位的准确性。为了研究基点和参考点的几何层次的效果，本文的实验采用N=5参考点，选择5 个不同的基点定位，分别代表5 种典型的几何形基点—参考点设置。本文SC-SDP 算法与GM-SDP 算法[13]和CRLB算法等的比较结果如表1 所示。

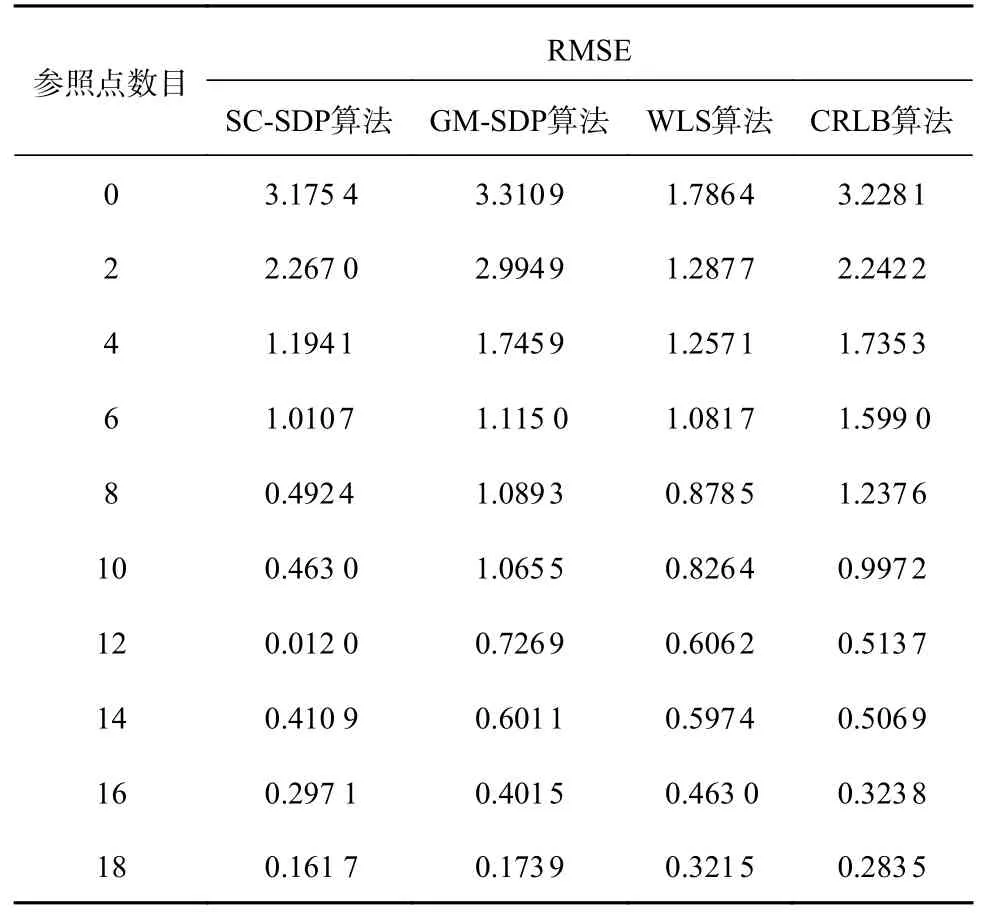
表1 不同算法的均方根方差Table 1 Root mean square variances of different algorithms

从表1 看出：当参照点数目逐渐增大时，均方根方差（RMSE）逐渐降低。当参照点数目增大到18 时，相比GM-SDP[13]算法、WLS 算法以及CRLB算法，SC-SDP 算法的均方根方差（RMSE）最优。因此，虽然参照点数目增多导致噪声增加，但是SC-SDP 算法的性能是递增的 。

5.2.2 半定松弛优化估计算法的实验分析

SC-SDP 算法是优化并去除半定松弛化算法产生的噪声，同时调整实验参数。本文的实验采用无迹卡尔曼滤波算法优化并缓解半定松弛化算法产生的噪声。本文拓展了无迹传送信道，获得推导和应用框架，有效地消除了几乎所有常见的非线性坐标变换的噪声偏差。图4 是添加卡尔曼过滤器之后的WLS 和SC-SDP 两种算法的定位误差比较结果。传感器数量增加也就间接导致位置误差增加。当最后传感器数目增加到20 时，SC-SDP 算法比WLS 算法定位误差大，但和 图5 添加卡尔曼过滤器之前的定位误差相比，SC-SDP 算法的定位误差也是降低的。

图4 WLS 和SC-SDP 的位置误差比较（添加卡尔曼过滤器之后）Fig.4 Comparison of position errors between WLS and SCSDP(After adding the Kalman filter)

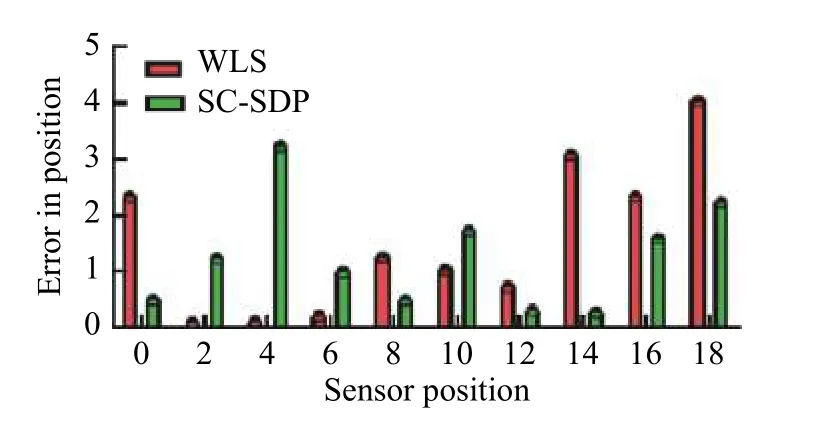
图5 WLS 和SC-SDP 的位置误差比较（添加卡尔曼过滤器之前）Fig.5 Comparison of position errors between WLS and SCSDP(before adding the Kalman filter)

图5 是增加卡尔曼过滤器之前的实验结果。采用WLS 算法和SC-SDP 算法计算出均方根方差，再通过均方根方差计算定位位置的误差。传感器数目刚增加时，定位误差快速递增，直到传感器数目增加到18 时，定位误差进入相对稳定的阶段，但是定位误差是增大的。

6 结束语

为提高无线传感网络室内定位精度，本文提出基于半定松弛优化估计算法的无线传感网络定位算法（SC-SDP 算法）。在半定规划算法的基础上，将算法的约束条件松弛化，使定位更加准确。同时采用无迹卡尔曼滤波（UKF）算法过滤信号传输过程中的噪声，对无线传感器网络定位进行精确分析。将SC-SDP 算法与WLS 算法、CRLB 算法进行比较实验和过滤噪声前后的比较实验。噪声没过滤前时，实验结果表明，随着传感器参考点位置数量的增加，定位误差呈上升趋势。因此，在采用无迹卡尔曼滤波（UKF）算法过滤掉传输过程中的噪声之后，定位误差呈递减趋势，半定松弛优化估计算法性能也得到提升。实验结果也表明SC-SDP算法的均方根方差（RMSE ）比GM-SDP 算法、WLS算法以及CRLB 算法的均方根方差更小。在未来的网络定位算法里，采用半定松弛优化估计算法来解决定位精度性能分析具有更加广阔的前景。