完全氧化DZ125的双向反射特性实验研究

叶志鹏，赵树男，李勋锋*，淮秀兰

1.中国科学院工程热物理研究所，北京 100190 2.中国科学院大学工程科学学院，北京 100049 3.中科南京未来能源系统研究院，江苏 南京 211135 4.空调设备及系统运行节能国家重点实验室，珠海格力电器股份有限公司，广东 珠海 519070

引 言

涡轮叶片作为航空发动机和燃气轮机的重要组成部分，其性能好坏对发动机有着直接的影响。在涡轮叶片的研究中，温度是十分重要的一个参数。目前对于涡轮叶片的测温，主要有接触式测温和非接触式测温两类[1]。而非接触式测温又以辐射测温技术为主。辐射测温技术，因其具有响应时间短，操作灵活，不会干扰流场、温度场，测温范围广等优点[2-4]，在涡轮叶片测温中具有很好的应用前景。

然而，辐射测温方法也有其缺点，就是容易受到周围环境影响。在使用辐射高温计对涡轮叶片进行测温时，被测叶片反射的来自周围其他热端部件的投射辐射，会对温度测量产生不小的影响，不能简单忽略。因此，为了保证辐射测温的可靠，有必要对涡轮叶片及其他热端部件的材料的反射特性进行研究。

双向反射分布函数(BRDF)是目前研究材料反射特性的主要方法。这一概念源于二十世纪六七十年代，最早被Nicodemus[5]明确定义。之后几十年间备受关注，经过Bartell等[6]学者长期的深入研究，时至今日，BRDF理论已经得到了较为完善的发展。国内外也有许多的学者根据这一原理成功测量了一些材料表面的双向反射特性[7-10]。

然而，直到目前，关于涡轮叶片材料反射特性的相关研究还很少。因此，本文将针对一种常见的涡轮叶片材料——完全氧化的镍基合金DZ125，开展相应的研究。在温度分别为25，900和1 100 ℃，波长分别为1 060，1 550和1 908 nm的条件下，采用对比法[6]测量完全氧化DZ125的双向反射分布函数，进而分析温度、波长、入射角、反射角等因素对BRDF的影响。

1 测量原理

建立如图1所示的坐标系，双向反射分布函数的定义式为

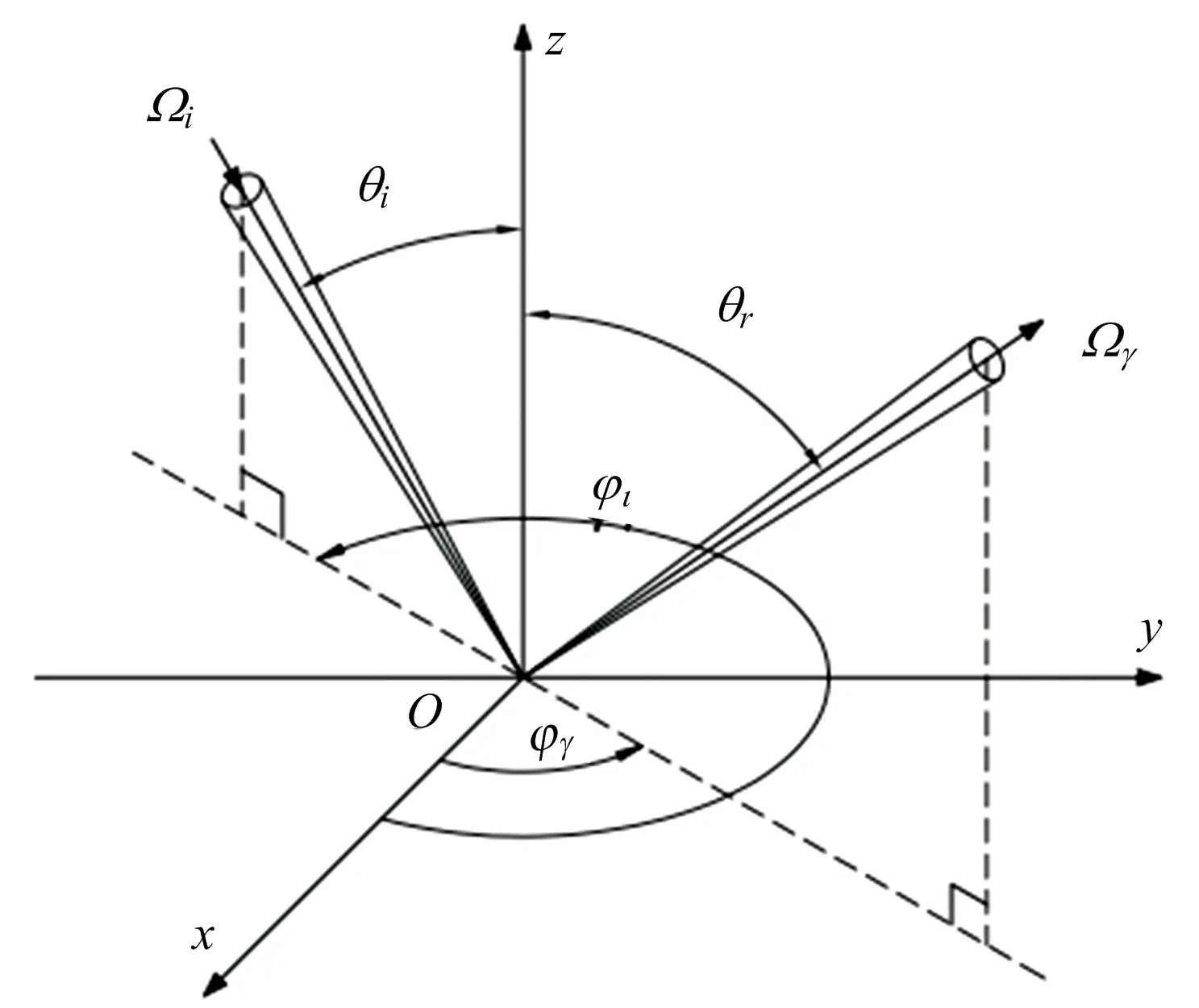
图1 BRDF几何关系示意图

(1)

式(1)中，θi表示入射天顶角；φi表示入射方位角；θr表示反射天顶角；φr表示反射方位角；Iλ(λ,θi,φi)表示入射方向为θi和φi时的入射辐射强度；dΩi表示入射辐射强度Iλ(λ,θi,φi)所对应的立体角；dIλ(λ,θi,φi,θr,φr)表示反射方向为θr和φr时的反射辐射强度。

本次实验采用的是对比法。在相同的入射和接收条件下，分别对完全氧化DZ125和标准漫射体的反射分布进行测量，相比可得

(2)

对于标准漫射体，有

(3)

将(3)式代入式(2)可得

(4)

式(4)中，dIλ, s(λ,θi,φi,θr,φr)和dIλ, ref(λ,θi,φi,θr,φr)分别表示待测试样和标准漫射体在入射方向为θi和φi，反射方向为θr和φr时的光谱反射辐射强度；ρλ, ref(λ)表示标准漫射体的定向半球反射率。

在实际测量中，为消除背景噪声对测量结果的影响，需要在有入射光和无入射光的条件下分别进行测量。因此，在使用FTIR光谱仪测量时，式(4)可以写成如式(5)形式

(5)

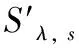
如此便实现了对待测试样BRDF的测量。通过改变入射激光波长、温度、入射天顶角、反射天顶角以及方位角等参数，可以得到不同情况下的BRDF变化规律。

2 实验部分

完全氧化DZ125的BRDF实验测量系统如图2所示。该实验装置主要由实验平台、转台、温度控制装置、FTIR光谱仪(NIR 2500, Ideaoptics)、激光发射探头、辐射接收探头、激光器、光纤和计算机等组成。

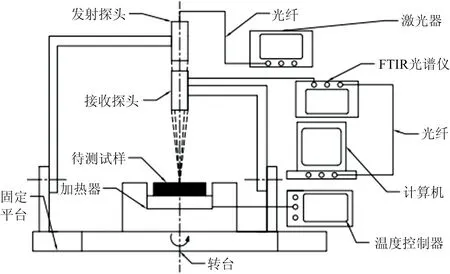
图2 BRDF测量系统示意图

选用光纤耦合激光器作为发射光源，辐射接收探头则用于接收反射辐射信号。温控装置用来加热试样，使其保持恒温。激光发射探头的转动臂被固定在实验平台上，辐射接收探头的转动臂安装在转盘上，可以与转盘进行-90°～90°的同步旋转。本系统采用步进电机实现对测量角度的精确控制，定位精度可以达到0.01°，消除了人为读数时的随机误差，参照赵忠义等[11]的分析方法对测量系统的误差进行分析，得到的总体测量误差不超过6%。

实验测试时，入射天顶角θi和反射天顶角θr的变化范围为0°～60°，间隔均为10°，入射方位角变化范围为0°～180°，间隔10°。实验选用的标准漫射体的直径为20 mm，当波长为1 060，1 550和1 908 nm时，其半球反射率分别为0.977，0.975和0.969。

3 结果与讨论

3.1 温度、波长对BRDF的影响

入射天顶角分别为θi=0°, 20°, 40°, 60°以及反射天顶角分别为θr=10°, 50°的情况下，不同波长、不同温度下完全氧化DZ125的BRDF测量结果如图3所示。

由图3可知，当波长相同时，BRDF的测量值随温度升高会略有减小，但是减小的幅度很小，当测量温度差别不大时，BRDF测量结果接近相等。并且，BRDF测量值的变化规律并不随温度变化而发生明显变化。可以认为，温度对BRDF的测量影响很小，在工程应用中可忽略从而使问题简化。

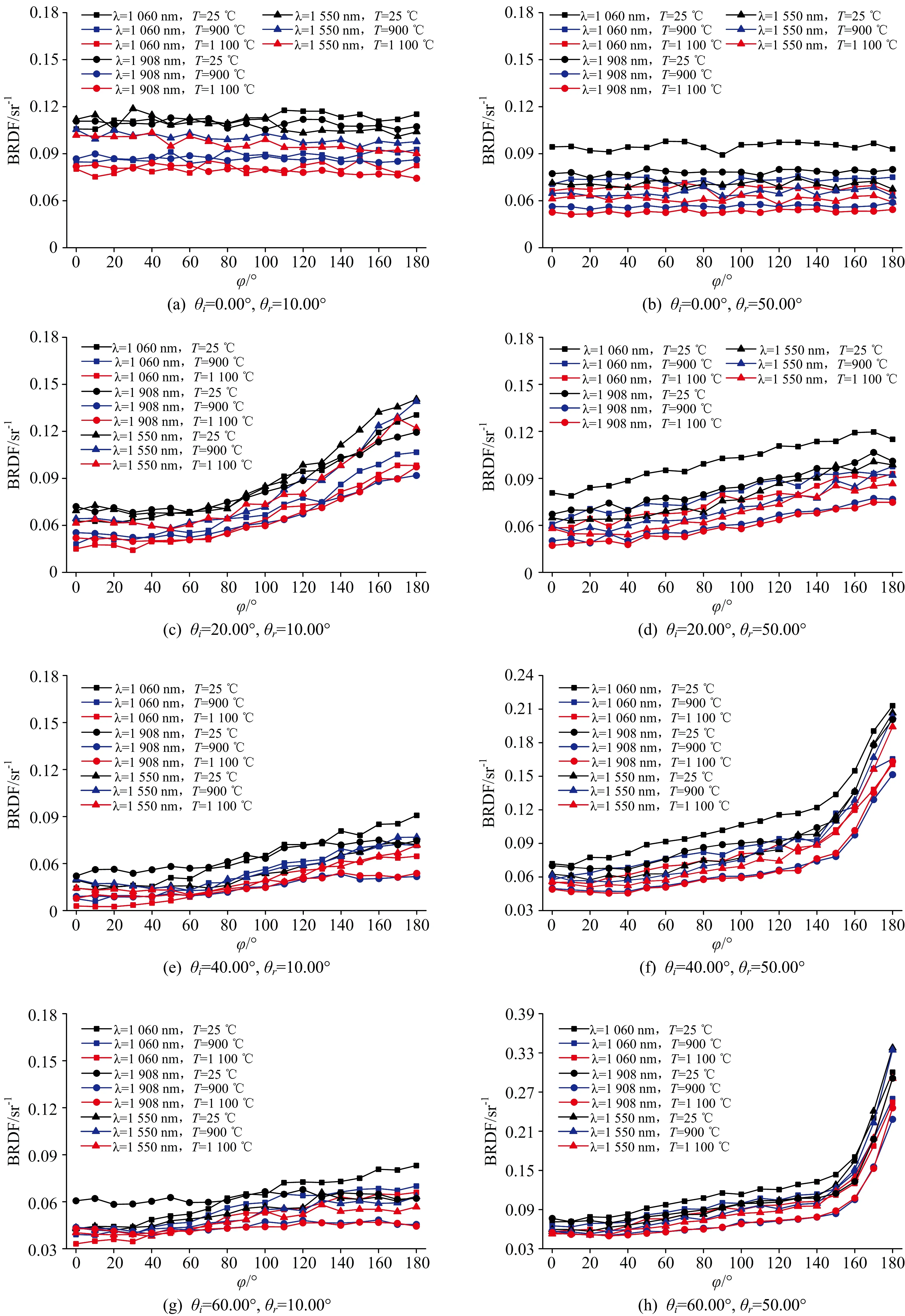
图3 温度和波长对完全氧化DZ125的BRDF的影响

相比于温度，波长对完全氧化DZ125的BRDF的影响较为复杂。如图3所示，当试样处于高温环境，即温度为900和1 100 ℃时，实验测得的BRDF的变化趋势基本一致。当反射天顶角θr=10°，入射角在0°～40°之间变化时，BRDF在波长为1 550 nm时取得最大值，在波长为1 908 nm时取得最小值；当反射天顶角θr=50°，入射角在0°～20°之间变化时，同一温度下，BRDF随着波长的增大而减小，在波长为1 060 nm时取得最大值，在波长为1 908 nm时取得最小值。

可以看出，在高温下，波长对BRDF测量值的大小会有一定的影响，天顶角不同，在不同波长下测得的BRDF之间的大小关系也会有所不同，这一现象产生的原因十分复杂，涉及到了材料表面微观结构的特性、光子与材料表面的相互作用等复杂的内在机理，有待日后进一步研究。然而，虽然波长变化，BRDF测量值略有变化，但是其变化的趋势基本是相同的，当波长变化范围不大时，BRDF测量结果差别不大，基本可以认为波长对BRDF不产生影响。

3.2 入射角对BRDF的影响

由前面的分析可知，完全氧化DZ125的BRDF的变化规律基本不随温度和波长的变化而变化。因此，下面以温度为1 100 ℃，波长为1 550 nm时的测量结果为例，分析入射角对完全氧化DZ125的BRDF的影响。

由图4不难看出，当反射天顶角不变时，入射天顶角不同，测得的BRDF也不同。当接收器探头相对于激光发射探头，恰好处于镜面反射位置(θi=θr,φ=180°)时，BRDF的测量值最大。因为光线的反射由镜面反射和漫反射两部分构成，镜面反射主要发生在镜面方向，而在其他方向，镜面反射会快速衰减，具有明显的方向性，而漫反射则没有明显的方向性，具有各向同性的特点。因此，当接收器探头远离镜面方向时，光线的反射以漫反射为主，能量较小，分布较为均匀；当接收器探头逐渐靠近镜面方向时，镜面反射逐渐占主导，能量较为集中，测得的BRDF值也变大，当探头到达镜面位置时，BRDF取到最大值。

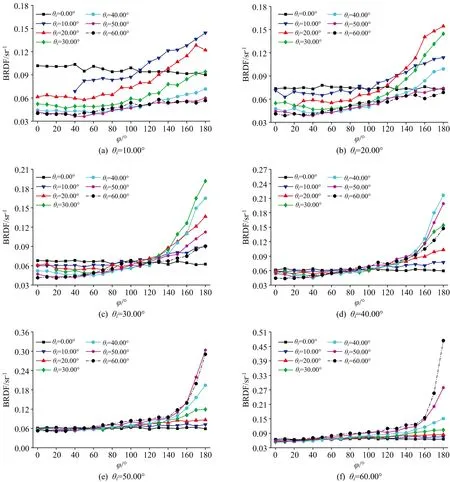
图4 当温度为1 100 ℃，波长为1 550 nm时，入射角对完全氧化DZ125的BRDF的影响

当反射天顶角θr较小时，可以很明显的看出，方位角存在着某一临界值φcr。当方位角φ小于这一临界值时，BRDF值随入射天顶角θi的增大而降低；大于这一临界值φcr后，规律发生变化，此时，入射天顶角越接近反射天顶角，BRDF的值越大。当反射天顶角θr逐渐增大后，φcr的值会逐渐减小，并且在φ<φcr处，BRDF随入射天顶角变化的差异也在逐渐变小，在θr≥50°时，BRDF测量值几乎看不出明显差异了。这一现象说明了反射天顶角θr较大时，在远离镜面方向处，光线经过完全氧化DZ125几乎不发生镜面反射。而当反射天顶角θr较小时，在远离镜面方向处会有微弱的镜面反射存在，完全氧化DZ125不是标准的漫射体。

3.3 反射角对BRDF的影响

以温度为1 100 ℃，波长为1 550 nm时的测量结果为例，分析反射角对试样BRDF测量值的影响，测量结果如图5所示。

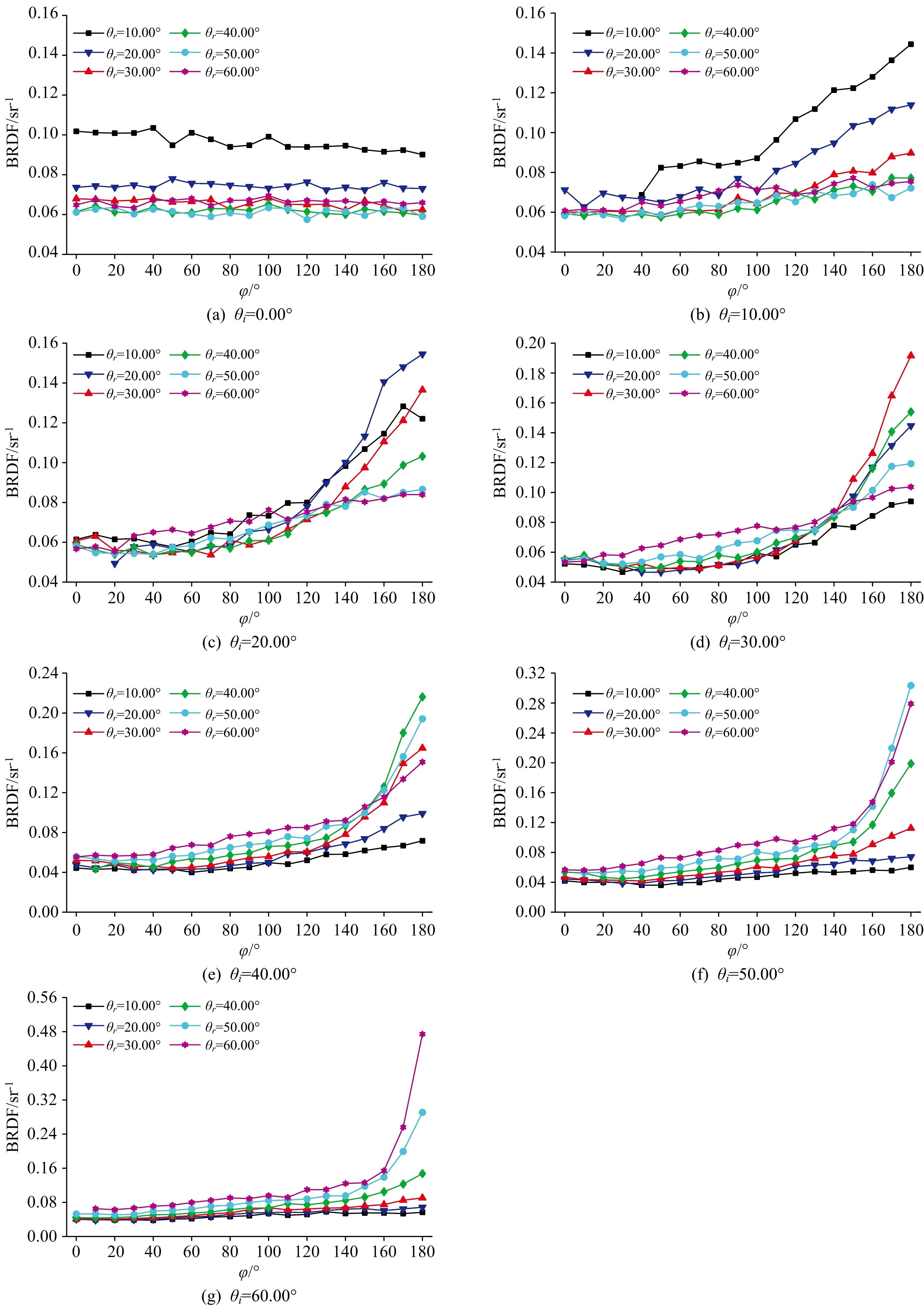
图5 当温度为1 100 ℃，波长为1 550 nm时，反射角对完全氧化DZ125的BRDF的影响

当入射天顶角θi=0°时，BRDF测量值基本不随方位角φ的变化而发生明显的变化，可以认为此时的BRDF沿着方位角方向各向同性。造成这种现象的原因是，当入射天顶角θi=0°时，入射光线相当于垂直照射试样，光线接触试样后，在沿着入射光线相反的方向(θr=0°)将主要发生镜面反射。因此，当θr>0°时，无论方位角φ如何改变，BRDF测量反射天顶角与镜面反射角之间的夹角是不变的，且是对称，辐射接收探头接收到的辐射能量为镜面反射分量和漫反射的叠加。由于漫反射各向同性，而镜面反射分量也绕天顶角0°角中心对称，所以测量得到的辐射强度相差不会很大，BRDF的变化也不大。与前面小节的分析类似，当接收探头越靠近镜面方向(θi=θr,φ=180°)，镜面反射的占比相对也越大，BRDF的值也就越大，故当入射天顶角θi=0°时，BRDF随反射天顶角θr的增大而减小。由于探头之间存在相互遮挡，不能直接测量反射天顶角θr=0°时的BRDF值，但是不难推断：当反射天顶角θr=θi=0°时，BRDF在反射天顶角θr=0°时取得最大值。

当θi≠0°时，在某一反射天顶角下，随着方位角的增大，BRDF测量反射角越接近镜面反射角，BRDF测量值会越大。BRDF测量值在镜面反射方向达到最大，且BRDF所能达到的最大值随入射天顶角θi的增大而增大。

3.4 方位角对BRDF的影响

根据图3—图5的内容综合分析可知，当方位角φ较小时，BRDF基本不随方位角φ变化而变化，当方位角大于某一临界值φcr后，BRDF的变化规律会因情况而有所不同。φcr的值随θi与θr的取值不同而有所不同。

如果入射天顶角θi与反射天顶角θr相差较小，即光线入射角与反射角越接近时，随着方位角φ的增大(即接收探头向镜面方向移动)，BRDF测量值会明显地增大，并且θi与θr越接近，BRDF增大得越明显，这说明了此时镜面反射占了主导。如果入射天顶角θi与反射天顶角θr相差较大时，随着方位角φ的增大，BRDF测量值基本保持不变，这说明了此时漫反射占了主导。

综合以上现象分析可知，被测试样的BRDF值的大小与测量角度关系密切，完全氧化DZ125具有很强的镜面反射特性。

3.5 模型拟合

3.5.1 Modified Phong模型

通过实验测量得到的BRDF只是几个离散的点，有时候为了使用诸如蒙特卡罗法等数值方法计算材料的辐射特性，需要得到连续的BRDF值，这时，往往需要通过建立合适的数学模型[12-15]来近似。

在众多的模型之中，由Lafostune和Willems[12]提出的Modified Phong模型因为具有Helmholtz互异性，遵循能量守恒定律，简单且适用于粒子追踪等优点，很适合作为数值模拟的模型。只要给定该模型的几个待定参数，就能使用蒙特卡洛方法等方法模拟计算了。不过该模型有一定的适用范围，在使用该模型对某种材料进行数值模拟之前，需要先用实验数据对其进行拟合，判断该模型能否正确反映出所研究材料的反射特性，然后再决定是否使用该模型进行数值计算。

为此，本节将采用Modified Phong模型对完全氧化DZ125的BRDF实测数据进行拟合，从而分析该模型是否能反映完全氧化DZ125的反射特性。

Modified Phong模型[12]的表达式如式(6)所示

(6)

式(6)中，kλ, d和kλ, s为漫反射系数和镜面反射系数，为了保证能量守恒，要求kλ, s+kλ, d≤1；n为镜向指数，n越大，表示材料的镜面反射特性越明显；α为光线的理想镜面反射方向和实际出射方向的夹角，为避免cosα取负值，令α=min(π/2,α)，由解析几何的方法易得

cosα=cosθicosθr-sinθisinθrcosφ

(7)

由实验测量得到不同的测量角度θi，θr以及φ下对应的BRDF值，由θi，θr以及φ可以求出cosα的值。kλ, s，kλ, d以及n都是待定系数，这是一个多参数优化的问题，本文采用遗传算法[16-17]对其进行拟合求解，将求解出的参数再回代到式(6)，得到了完全氧化DZ125所对应的BRDF理论模型曲线。

3.5.2 拟合结果分析

忽略温度和波长对BRDF的影响，对完全氧化DZ125在温度为900和1 100 ℃及波长为1 060，1 550和1 908 nm的测量结果进行算术平均，将算术平均结果代入式(6)，采用遗传算法对数据进行拟合，得到的拟合参数为：kλ, d=0.184 3，kλ, s=0.029 29，n=21.213 7；均方根误差(RSME)为0.021 9，相关系数(r)为0.724 2。通过拟合得到的镜向指数n较大，这说明了完全氧化DZ125具有很强的镜面反射能力，与前面章节的分析一致。将拟合参数代回Modified Phong模型，可以计算出不同角度下的BRDF值，结果如图6所示。

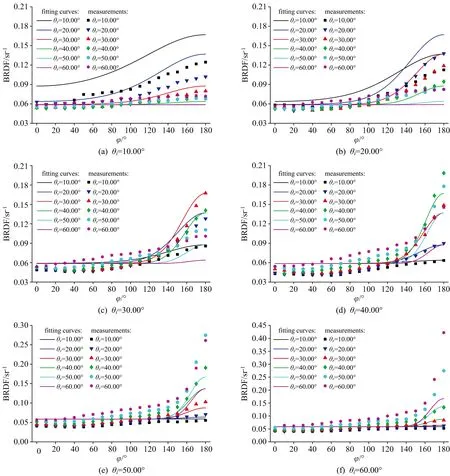
图6 完全氧化DZ125的Modified Phong模型拟合结果

通过对比可以发现，除了θi=10°，θr=10°的情形，在远离镜面方向处，由Modified Phong模型拟合得到的BRDF数值基本相同，不随反射天顶角θr和方位角φ变化。而BRDF的实测结果则是，在远离镜面方向处BRDF值会随反射天顶角θr和方位角φ变化而发生微小的变化。这一现象表明：通过Modified Phong模型计算，预测在远离镜面方向处不存在镜面反射，只有漫反射。而实际情况则是完全氧化DZ125在远离镜面方向并不是只发生漫反射，还存在微弱的镜面反射。模型与实际之间存在一些差别。

可以看到，当入射天顶角θi为30°和40°时，拟合结果与实验数据吻合得较好；当入射天顶角较小时，计算得到的BRDF高于实测值，Modified Phong模型高估了完全氧化DZ125的镜面反射能力；当入射天顶角较大时，情况则刚好相反，Modified Phong模型低估了其镜面反射能力。

上述现象表明：完全氧化DZ125具有很强的镜面反射特性，入射天顶角不同，BRDF的变化范围很大。Modified Phong模型是理想模型，无法对不同入射天顶角条件下的BRDF都做出准确计算。但是在大部分情况下，由Modified Phong模型计算得到的结果与实验数据都能较为吻合，BRDF模型拟合结果的变化趋势与实际测量BRDF的变化趋势基本一致，能够较好地反映完全氧化DZ125的反射特性，借助此模型，可以采用蒙特卡罗法对完全氧化DZ125的双向反射特性进行模拟研究。

4 结 论

采用了对比法，对完全氧化镍基合金DZ125在温度为25，900和1 100 ℃以及波长为1 060，1 550和1 908 nm的情况下的双向反射分布函数BRDF进行了测量，并对测量结果进行了相应的分析。实验结果表明：

(1)相较于入射角和反射角的影响，波长和温度对BRDF测量的影响较小。当波长和温度变化时，虽然测量值的大小会略有差别，但是BRDF测量值总体的变化规律无明显变化。当波长和温度变化不大时，可以忽略二者对BRDF的影响。

(2)入射天顶角θi以及反射天顶角θr对完全氧化DZ125的BRDF测量值影响十分明显。二者取值越接近，则BRDF的测量值也就越大。当激光发射探头与辐射接收探头处于镜面方向(θi=θr,φ=180°)处，BRDF取到最大值，而且入射天顶角θi越大，BRDF能取到的最大值也越大。

(3)方位角对BRDF测量值的影响，与θi和θr紧密相关。当方位角φ较小时，各向同性的漫反射在BRDF中占据主导，所以BRDF基本不随方位角φ变化而变化。当方位角大于某一临界值φcr后，BRDF变化趋势会因θi和θr取值而有所不同。当θi和θr十分接近时，此时镜面反射成了主导因素，BRDF测量值会随着φ的增大而增大，且θi和θr相差越小，BRDF增大得越快。当θi和θr相差很大时，此时漫反射占比较大，BRDF测量值基本保持不变。

(4)采用Modified Phong模型拟合的结果能够较好地反映完全氧化DZ125材料的反射特性，可用于蒙特卡罗法计算。由Modified Phong模型计算的结果分析可知，完全氧化的DZ125材料，具有极强的镜面反射特性。