基于最短路径的GNSS-R镜面反射点算法
刘原华, 贺立庆, 牛新亮
(1.西安邮电大学 通信与信息工程学院, 陕西 西安 710121; 2.中国空间技术研究院 西安分院, 陕西 西安 710000)
全球导航卫星系统反射信号(global navigation satellite systems-reflectometry, GNSS-R)技术利用导航卫星伪随机测距码或者载波的反射信号,提取目标反射面特征[1]。与基于后向散射单基工作模式的卫星散射计和雷达高度计相比,GNSS-R技术采用扩频通信技术,拥有大量信号源,被广泛应用于海面测高[2]、海面测风[3-6]、海洋盐度[7]和土壤湿度[8]探测等领域。
在处理反射信号时,GNSS-R遥感器搜索和捕获信号的参考中心为镜面反射点,精确定位镜面反射点具有重要的意义[1]。定位GNSS-R镜面反射点的算法有很多,最先被提出的是Gleason算法[9],该算法采用单步定长线性迭代法,对镜面反射点进行粗估算后,利用校正增益系数不断收敛校正,使得新旧反射点之差达到指定的公差,从而得到精确的镜面反射点。但Gleason算法收敛次数多,算法效率低。针对这些缺点,文[10]提出了角平分线变步长算法[10],该算法在Gleason算法的基础上通过改进校正增益系数,降低了收敛次数。但是,收敛次数仍较多,算法效率低。为了进一步提高算法效率,Wu S C算法[11]利用几何关系得到初值镜面反射点,不断判断入射角和反射角的大小并进行收敛校正,最终得到精确的镜面反射点。但Wu S C算法未考虑椭球面上径向和法向的差异,导致定位误差。针对这一缺陷,线段二分法[12]通过不断地二分发射机和接收机构成的线段来获得满足条件的镜面反射点。但是线段二分法在判断收敛条件时,需要不断地调整入射角和反射角的大小并进行迭代计算。而用角度当作收敛判断条件时,GNSS-R几何关系中的入射角和反射角与斯涅尔定律中定义的入射角和反射角不同,导致定位存在一定误差。
为了提高GNSS-R镜面反射点的测量准确度与算法效率,本文采用全球定位系统(global position system, GPS)反射信号为研究对象,拟从GNSS-R镜面反射点的定义[1]出发,利用反射路径长度最短作为收敛判断依据,迭代计算出镜面反射点的位置信息。
1 镜面反射点几何关系及其定义
1.1 镜面反射点的几何关系
GNSS-R镜面反射点的几何关系模型如图1所示。其中S表示镜面反射点的位置,T为卫星发射机的位置,R为卫星接收机的位置,Rt和RR分别表示发射机和接收机到镜面反射点的距离,θT表示发射机相对于镜面反射点与地球面法线之间的夹角(入射角),θR为卫星接收机相对于镜面反射点与地球面法线之间的夹角(反射角),Re表示地球半径。
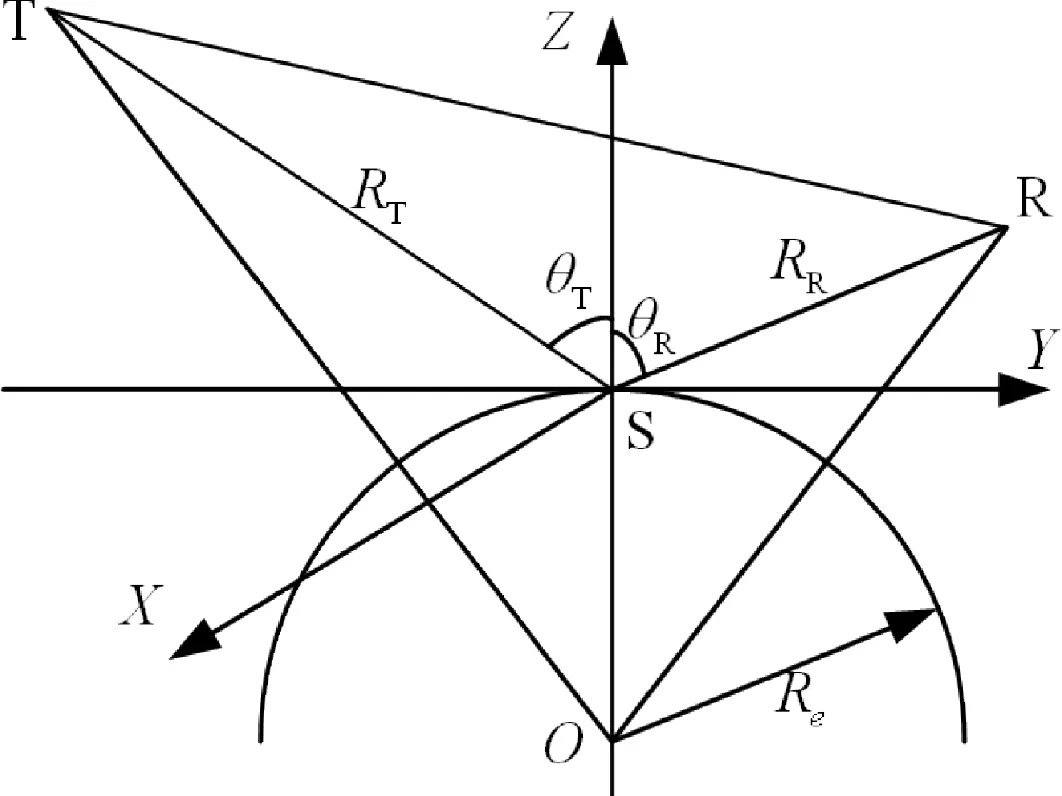
图1 GNSS-R镜面反射点的几何关系
1.2 镜面反射点定义及其特征
GNSS-R镜面反射点是GPS卫星发射机经反射点到接收机的路径最短的点[1]。令GNSS卫星发射机在WGS-84参考系中的位置坐标为(xT,yT,zT);GNSS卫星接收机在WGS-84参考系中的位置坐标为(xR,yR,zR);镜面反射点在WGS-84坐标系中的位置坐标为(xS,yS,zS)。
反射路径的长度fS的数学表达式为
当且仅当fS取最小值时,(xS,yS,zS)为镜面反射点的位置坐标。
GNSS-R镜面反射点有3个特征[13],即镜面反射点必定位于地球表面;镜面反射点是卫星发射机经反射点到接收机路径最短的点;镜面反射点满足斯涅尔定律,即在镜面反射点处,其入射角等于反射角。
2 基于最短路径的镜面反射点定位
2.1 最短路径的原理
在迭代计算时,本文缩小收敛区间的判断依据是比较反射路径的长度,最终在给定的精度范围内找到最短反射路径对应的镜面反射点的位置信息。
算法迭代计算的几何关系如图2所示,卫星发射机T位置坐标表示为向量a=[xT,yT,zT],卫星接收机R位置坐标表示为向量b=[xR,yR,zR],Sa,Sb分别为T,R 2点的星下点,∠TOR的角平分线与线段TR交点为P,其星下点为SP,C点为线段TR的二分点,其星下点SC。

图2 最短路径法迭代计算的几何关系
为了避免采用单个点P做判断出现的错判舍弃区间错误,在应用最短路径法确定镜面反射点的迭代计算时,需要在线段TR中插入点P和C。通过判断点P和C的位置,判断反射路径的长度,舍弃较长的反射路径所处的区间,从而保证较短的反射路径所处的区间被留下,提高算法的准确性。
2.2 最短路径法的步骤
最短路径法的步骤如下。
步骤1确定初始搜索区间为线段TR,设定精度ε为1米。
步骤2计算卫星发射机T与接收机R的星下点Sa和Sb的坐标向量,其表达式分别为
步骤3求∠TOR的角平分线与线段TR的交点P及线段TR的中点C的位置坐标。并且,分别求得P,C 2点星下点Sp,SC的位置坐标。
步骤4若Sa与Sb之间的距离小于精度ε,则镜面反射点设定为SP,结束;否则转步骤5。
步骤5分别计算发射机位置T和接收机位置R到星下点位置SP与SC的反射路径长度
fSP=|TSP|+|RSP|,fSC=|TSC|+|RSC|。
步骤6判断SP与SC的位置。若Sa与SP之间的距离小于Sa与SC之间的距离,则转步骤7;否则转步骤8。
步骤7若fSP 步骤8若fSP≤fSC,则将C点设定为T点,新的搜索区间为线段CR,转步骤2;否则将P点设定为R点,新的搜索区间设为线段TP,转步骤2。 最短路径法的流程如图3所示。 图3 最短路径法的流程 使用来自英国UK-DMC卫星于2004年11月16日测到的海洋数据中的3组数据来验证,数据组1发射机的位置坐标为(1 366 322.127 94,-23 127 631.879 20,-11 982 698.916 85),接收机的位置坐标为(335 492.491 51,-6 460 107.391 44,-2 813 071.858 19);数据组2中发射机的位置坐标为(-11 178 791.991 29,-13 160 191.204 99,20 341 528.127 54),接收机的位置坐标为(-4 069 896.703 38,-3 583 236.963 73,4 527 639.271 75);数据组3中发射机的位置坐标为(-11 130 828.076 797,-13 167 090.702 929,20 363 562.269 411),接收机的位置坐标为(-4 163 790.851 951 254,-3 618 216.540 713 221,4 413 520.900 955 853)。采用WGS-84地球椭圆模型中的地球半径值作为地球半径。利用MATLAB软件仿真。 由GNSS-R镜面反射点的3个特征可知,镜面反射点的位置必定在地球表面。仿真数据组1计算出的大地坐标系下镜面反射点位置信息为南纬23°64′37″,西经87°02′71″,高度为0;数据2的位置信息为北纬40°05′03″,西经138°63′84″,高度为0;数据组3的位置信息为北纬38°85′12″,西经139°01′03″,高度为0。满足了GNSS-R镜面反射点的位置必须在地球表面这一特征。 根据定义,GNSS-R镜面反射点是卫星发射机经反射点到接收机路径最短的点。数据组1、2、3的反射路径长度曲线分别如图4所示。 图4 反射路径长度曲线 可以看出,数据组1、2、3分别在迭代21、23、23次时,反射路径的长度达到最小并趋于稳定,从而满足了反射路径最短要求。 根据斯涅尔定律,在GNSS-R镜面反射点处,其入射角等于反射角。数据组1、2、3的入射角与反射角绝对值之差曲线如图5所示。 图5 入射角与反射角的绝对值之差曲线 可以看出,最短路径法的收敛速度较快,当迭代10次后,入射角与反射角的绝对值之差趋于零,即2角相等。满足了GNSS-R镜面反射点入射角等于反射角的要求。 以上表明所提出的算法满足了GNSS-R镜面反射点定义的3个特征,证明了算法的正确性。 为了验证最短路径法的效率,分别采用Gleason算法、线段二分法与最短路径法计算镜面反射点,不同算法确定的镜面反射点位置坐标和迭代次数如表1所示。可以看出,Gleason算法的迭代次数最多,效率最低,而线段二分法和最短路径法的迭代次数相当,效率相当。 表1 不同算法确定的镜面反射点位置结果对比 最短路径法的收敛迭代次数相较Gleason算法的4 600多次,效率提升了98%以上。其原因在于Gleason算法的收敛判定方法为单步定长线性迭代,收敛缓慢,甚至可能不收敛。而最短路径法确定的收敛区间内有且仅有1个最短的反射路径长度,必定收敛。所以,最短路径法的迭代次数较Gleason算法少,算法效率较高。 接下来验证算法的准确性。由于Gleason算法的迭代次数在4 600次以上,算法效率较低,所以,仅比较算法效率相当的最短路径法与线段二分法在迭代停止时,镜面反射点处的反射路径长度。反射路径长度越短,说明算法的准确性越高。2种算法迭代停止时的反射路径长度曲线如图6所示。 (a) 数据组1 (b) 数据组2 (c) 数据组3图6 两种算法迭代停止时的反射路径长度曲线 在迭代停止时,对数据组1采用最短路径法和线段二分法确定的镜面反射点处的反射路径长度分别为1.358 574 761 106 m和1.358 846 186 106 m;对数据组2采用最短路径法和线段二分法确定的镜面反射点处的反射路径长度分别为1.389 822 487 106 m和1.389 927 239 106 m;对数据组3采用最短路径法和线段二分法确定的镜面反射点处的反射路径长度分别为1.389 594 236 106 m和1.389 852 134 106 m。可以看出,采用最短路径法计算出的镜面反射点处的反射路径长度均少于线段二分法,说明最短路径法的准确性高于线段二分法。原因在于,线段二分法采用角度判定作为收敛判定方法,该判定方法的几何关系中入射角与反射角是由地球球心与镜面反射点的连线来确定,而不是由地球表面的平面法线确定的。在斯涅尔定律中,入射角、反射角是平面法线与入射线和反射线所形成的夹角,因此用角度作为收敛判断条件存在一定的误差。最短路径法的判定方法是寻找最短反射路径长度,而GNSS-R镜面反射点的定义是卫星发射机经反射点到接收机路径最短的点。因此,最短路径法满足了GNSS-R镜面反射点定义的要求,算法结果更加准确。 综上所述,最短路径法计算出的结果满足了GNSS-R镜面反射点的3个特征,证明了该算法预测GNSS-R镜面反射点的正确性;且与Gleason算法和线段二分法相比,最短路径法在算法效率与准确性上有一定的优越性。 基于GNSS-R的基本几何关系与镜面反射点定义,提出了一种用最短反射路径作为收敛判断条件来计算镜面反射点位置信息的方法。该算法在卫星发射机与接收机形成的线段上,插入该线段二分点以及由发射机、地球球心与接收机3点所形成角的角平分线和发射机与接收机形成线段的交点。计算并比较该两点的星下点的反射路径长度,在给定的精度范围内找到最短反射路径对应的镜面反射点的位置坐标。利用MATLAB软件仿真,结果显示,最短路径法满足镜面反射点的3个特征,可以正确定位镜面反射点。算法的收敛迭代次数与线段二分法基本相当,远低于Gleason算法。与线段二分法相比,算法的准确性较高。
3 仿真结果及分析
3.1 算法的正确性


3.2 算法的效率

3.3 算法的准确性



4 结语

