改进的灰色模型及其在网络舆情预测上的应用
张仲荣, 崔舒为, 徐 森
(兰州交通大学 数理学院, 甘肃 兰州 730070)
网络媒体的衍生与发展促进了网络舆情的产生与传播,网络舆情的演化影响着社会的稳定与发展[1]。 相对真实消息而言,虚假消息传播的更快更广,人们更倾向于分享与交流虚假信息。因此,对网络舆情进行良好的引导与控制尤为重要[2]。
利用科学的数据分析对舆情的演化行为进行预测与判断,可更好的控制与干预舆情的传播与发展[3]。 如改进的Hegselmann-Krause舆论演化模型改善了模型中缺乏个体对领袖观点持排斥意见的问题[4]; 灰色模型GM(1,1)对网络舆情事件可进行定量预测,取得了较好的效果,但预测精度较差[5]。 模拟近似非齐次指数序列的灰色模型NGM(1,1,k)改善了GM(1,1)对非齐次指数序列建模精度较差的问题[6];非齐次灰色模型NHGM(1,1)相对于NGM(1,1,k),对近似非齐次指数序列数据的包容性更好,预测效果更佳[7]。但是,这两种模型均存在参数估计与时间响应式之间的跳跃替代误差,预测精度仍有提高的空间。而三参数灰色模型TPGM(1,1)[8]的参数估计与时间响应式皆由差分方程推导得出,进一步避免了跳跃替代误差,但其初始值的选取方式并不是最优。
为了对网络舆情搜索指数数据预测更精确,本文建立一种改进的三参数灰色模型TPGM(1,1)。将几何平均弱化缓冲算子作用于初始数据,减少由于冲击扰动项的干扰造成的数据失真;引入TPGM(1,1),利用最小二乘法对TPGM(1,1)初始值的计算方法进行改进,以期提高预测精度。
1 三参数灰色模型TPGM(1,1)
针对网络舆情搜索指数数据的小样本特点,选择TPGM(1,1)进行网络舆情序列预测建模。TPGM(1,1)的参数估计与时间响应式皆由差分方程推导得出,避免了GM(1,1)从微分方程到差分方程的跳跃替代误差,预测精度更高。TPGM(1,1)建模过程[8]如下。
设初始序列
X(0)=[x(0)(1),x(0)(2),…,x(0)(n)],x(0)(k)≥0,k=1,2,…,n。
X(0)的一阶累加生成(accumulating generation operater,1-AGO)序列为

(1)
X(1)的紧邻均值生成序列为
Z(1)=[z(1)(2),z(1)(3),…,z(1)(n)],z(1)(k)=0.5[x(1)(k)+x(1)(k-1)]。
(2)
设定参数a、b和c,得TPGM(1,1)的表达式为
x(0)(k)+az(1)(k)=0.5(2k-1)b+c。
(3)
由式(1)、式(2)和式(3)可得方程组
(4)
解方程组(4)得
x(1)(k)-x(1)(k-1)+
0.5ax(1)(k)+0.5ax(1)(k-1)=
0.5(2k-1)b+c。
由此可推得
(5)
令
则式(5)可化简为
x(1)(k)=φ1x(1)(k-1)+φ2k-φ3,k=2,3,…,n。


(6)
要求
(7)
由φ1,φ2,φ3可知,

(8)
利用数学归纳法,推导式(8)得到时间响应式为
即
还原式为
(9)
根据式(9),利用TPGM(1,1)对网络舆情搜索指数数据模拟与预测。但是,TPGM(1,1)是以x(0)(1)为初始值作为条件,初始值的选取方式并不是最优。
2 改进的三参数灰色模型TPGM(1,1)
网络舆情数据的变化趋势并不能完全正确地展现出数据本身真正的变化规律, 冲击扰动项的存在阻挡了数据真实变化规律[9]。利用几何平均弱化缓冲算子对原始序列进行预处理,去除数据中的冲击扰动项[10-11],然后引入TPGM(1,1),利用最小二乘法对其初始值的计算方法进行改进。
2.1 几何平均弱化缓冲算子
设系统真实序列为X(0),观测序列[9]为
X=[x(1),x(2),…,x(n)]=
[x(0)(1)+ε1,x(0)(2)+ε2,…,x(0)(n)+εn]=
X(0)+ε
其中ε=(ε1,ε2,…,εn)为冲击扰动项,则X也称为冲击扰动序列。
将几何平均弱化缓冲算子作用于冲击扰动序列X,得到去除冲击扰动项序列[9]
XD=[x(1)d,x(2)d,…,x(n)d]
其中
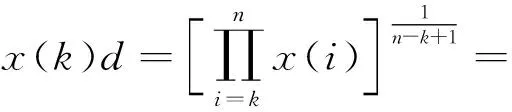
2.2 TPGM(1,1)的初始值优化
利用最小二乘法对TPGM(1,1)的初始值进行改进,以模型的整体模拟误差最小为目标选取初始值,也就是解决最优化问题
(10)

解得
3 实例分析
3.1 数据的选取与预处理
利用热门关键词“IG夺冠”的百度指数[12-13]作为舆情数据对改进的TPGM(1,1)进行检验。根据舆情搜索指数的变化具有急剧变化的特点,指数在一到两日之内就会达到最高峰,然后缓慢下降最终趋于稳定。所以从搜索指数的最高点开始选取数据,选用2018年11月3日至11月17日的百度指数(舆情序列)作为初始数据,划分11月3日至11月12日为训练集,11月13日至11月17日为测试集,对11月13日至11月17日“IG夺冠”的百度指数进行预测。数据的选取与处理结果如表1所示。

表1 原始数据与预处理数据
由表1可以看出,经过几何平均弱化缓冲算子处理后,数据展示出了原本真实的变化规律,还原了数据的真实面目,将更有利于之后的数据建模。
3.2 结果对比分析
利用评价指标相对误差、平均相对误差、平均绝对百分比误差(mean absolute percentage error,MAPE)和均方误差(mean square error,MSE)[14-15],对比GM(1,1)、TPGM(1,1)和改进的TPGM(1,1)的预测结果分别如表2和表3所示。
由表2和表3可以看出,TPGM(1,1)相对于GM(1,1)指标均变小,说明移除参数替代误差后预测精确度更高,而改进的TPGM(1,1)比TPGM(1,1)的预测精度还有所提升,说明基于最小二乘法改进初始值的选取方法是有效的。因此,改进的TPGM(1,1)的预测精度更高。

表2 3种模型的预测结果

表3 3种模型的MAPE与MSE对比
4 结语
引入几何平均弱化缓冲算子对初始数据进行预处理,然后利用最小二乘法对TPGM(1,1)的初始值进行改进,最终建立改进的TPGM(1, 1)。实验结果表明,改进模型比GM(1,1) 和TPGM(1,1)的预测精度更高。

