车联网中基于麻雀搜索算法的计算卸载策略
杨 超,王宗山,聂仁灿,丁洪伟+,李 波
(1.云南大学 信息学院,云南 昆明 650504; 2.云南大学 云南省高校物联网技术及应用重点实验室,云南 昆明 650504)
0 引 言
车联网技术的快速发展使得车载终端的业务环境更加复杂,出现了大量的计算密集型和时延敏感型业务,例如:自动驾驶、实时路况和语音识别等[1,2]。这些任务不仅数据量较大,而且对处理的实时性具有较高要求,因此完成此类业务的计算需要消耗大量计算资源。然而,车辆有限的计算资源将难以满足此类计算任务的时延需求[3]。为解决这一问题,边缘计算(mobile edge computing,MEC)作为一种新兴的技术被引入到车联网中,能有效降低任务执行时延,减少车辆本地计算资源占用,从而极大提升用户体验[4]。
计算卸载作为MEC的关键技术之一,是有效提升任务处理效率和减少计算时延的重要手段。目前车联网场景下的MEC系统(MEC-based vehicular network system,VEC)计算卸载主要解决车载应用任务是否需要卸载以及为每个计算任务分配多少资源的问题。现有研究主要从减少MEC系统资源服务费[5]、最小化任务执行时延和设备能耗[6,7]、车辆在动态环境中的任务调度策略[8]、内容驱动的计算卸载策略[9]、基于优先级划分的任务卸载策略[10]入手解决车载应用的计算卸载问题。但是,上述方案没有同时考虑VEC系统中计算任务优先级划分和车联网动态场景下的计算卸载决策,且算法收敛速度慢。
针对目前研究存在的问题,本文综合考虑了车联网动态场景下的计算卸载决策和任务优先级划分,使得紧急的任务优先得到处理。本文以最小化VEC系统的计算时延和MEC资源服务费为目标,提出一种基于麻雀搜索算法的计算卸载策略,在保证紧急任务优先得到处理的同时均衡系统中MEC服务器负载,提高任务处理效率。
1 系统模型
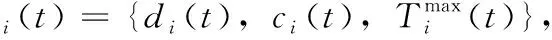
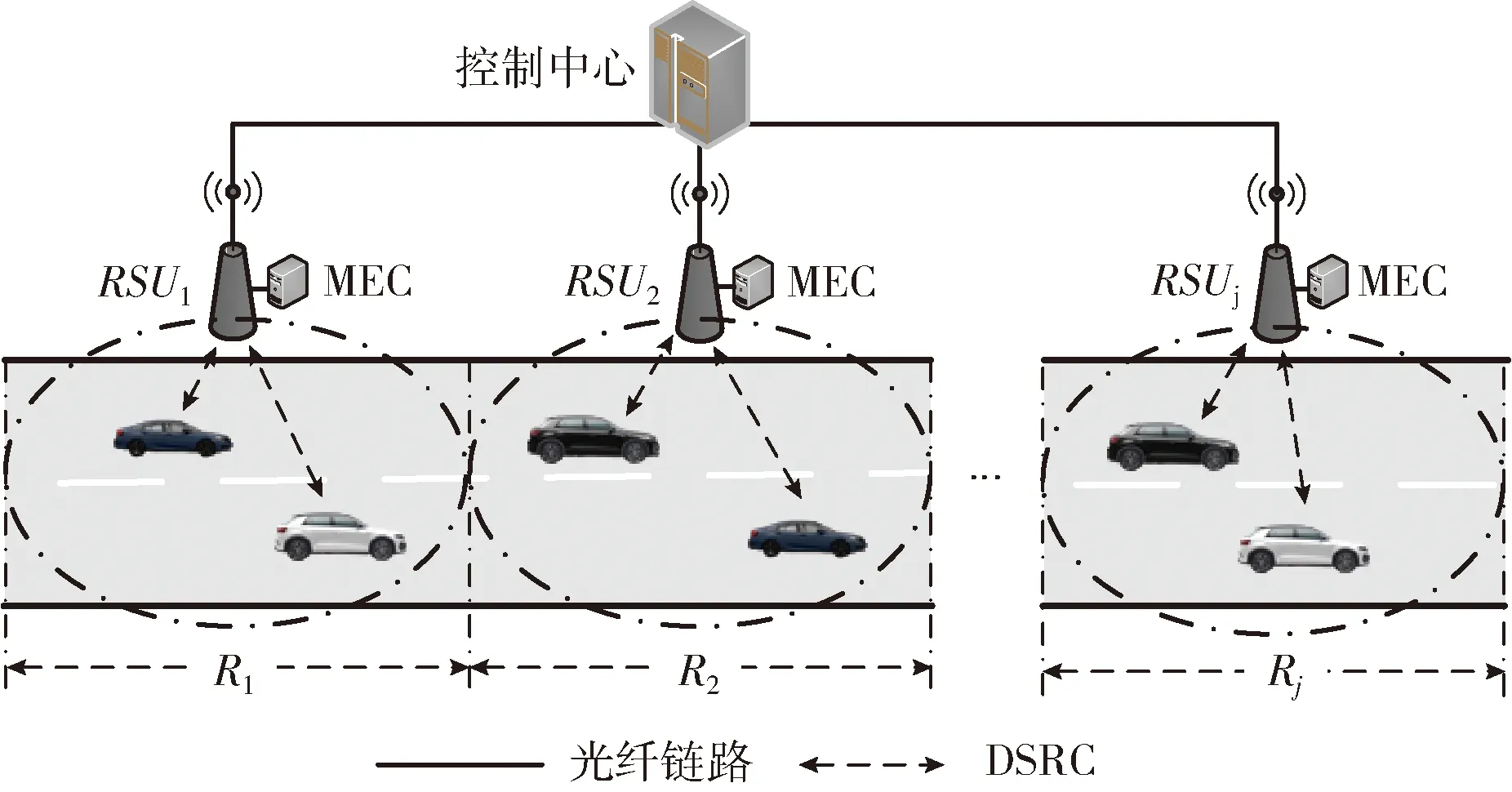
图1 车联网计算卸载模型
1.1 计算卸载模型
为了使系统中的计算资源得到充分利用,车辆i产生的计算任务Ti(t) 可以在本地执行(all local process,ALP)也可以卸载到MEC(all offload to mec process,AOMP)服务器执行。本文把t时刻任务Ti(t) 的卸载决策变量定义为xij(t) 且其值只能取0或1,即xij(t)∈{0,1}, 其意义可表示为
(1)
此外,由于计算任务不可分解,因此t时刻任务Ti(t) 只能选择一种卸载策略,即xij(t) 中的元素只有一个元素为1其余全为0,该约束条件可表述为
(2)
则t时刻所有车辆的卸载决策矩阵可定义为
(3)
为了方便描述,本文把计算任务在本地和MEC服务器处理的集合分别定义为Nl={i∈N|xi0(t)=1} 和No={i∈N|xij(t)=1},j∈M。
1.2 通信模型
假设图1所述场景中车辆i在道路上以速度vi匀速行驶,车辆i的移动使其与第j个RSU之间的距离dij也时刻在产生变化,则dij可定义为
(4)

当车辆把计算任务卸载到MEC服务器执行时,车辆需要与RSU进行通信,其上下行链路可以建模为频率平坦型快衰落的瑞利信道[13]。则由香农公式可以把车辆i上传数据至RSUj的传输速率定义为
(5)
其中,B为上行链路带宽;pi为车辆i的发射功率;σ2为背景噪声方差[14]。hij(t) 为车辆i与RSUj之间的信道增益,其可以通过车辆与RSU之间的直线距离进行计算[15],即
hij(t)=103.8+20.9log10dij(t)
(6)
1.3 计算模型
在此VEC系统中,车辆可以将计算任务卸载到计算资源较为充足的MEC服务器处理或选择直接在本地处理。当车辆将任务卸载到MEC服务器处理时,对应的MEC服务器将会为其分配计算资源,同时用户也将根据计算资源的使用情况向运营商缴纳费用。因此,本文主要以车辆处理任务的总时延和MEC资源服务费的加权和来衡量整个系统的性能。
1.3.1 MEC卸载模型
当车辆把计算任务Ti卸载到MEC服务器处理时,任务的处理的总时延为任务上传时延和任务计算时延。此外,由于RSU的发射功率远大于车辆且计算结果的数据量远小于任务上传的数据量,因此计算结果回传的时延可以忽略[16]。则车辆i在t时刻与RSUj的传输时延可定义为
(7)
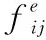
(8)
此外,运营商还将根据用户使用MEC资源的多少来收取服务费[17]。若把MEC服务器计算资源的单价定义为ρ,则车辆i的计算开销φij(t) 可写为
(9)
综上,车辆i在MEC服务器j处理任务的效用函数可定义为
(10)
其中,μi∈[0,1] 为车辆i对时延和资源服务费的偏好。
1.3.2 本地处理模型
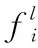
(11)
因此,t时刻车辆i本地计算的效用函数为
(12)
此外,为保证车辆计算任务的连续性及在限定时间内完成任务卸载,则任务卸载的总时延不应超过该任务的最大容忍时延Tmax,且要求任务计算卸载在车辆离开RSU的覆盖范围前完成,这两个约束条件可表示为
(13)

1.4 任务优先级处理
当车辆需要将计算任务卸载时,由于每个任务的数据量大小,最大时延容忍度和任务类型不同,导致需要分配的计算资源和处理顺序也不同。因此本系统将对卸载的任务进行优先级划分,保证紧急的任务优先处理[18]。本文采用层次分析法(analytic hierarchy process,AHP)来划分任务的优先级,通过AHP算法给每个任务分配处理的优先级,使得紧急的任务得到优先处理,进而实现更合理的卸载决策。
(14)
采用特征向量法计算,每个任务中影响因素的权重即
Aβ=λmaxβ
(15)
其中,β为权重向量,λmax为矩阵A最大的特征值。
由β及各影响因素即可算出任务Ti在t时刻的分数Ci(t)
(16)
最后,对所有任务的分数进行归一化处理即为对应任务的优先级,把执行任务的优先级向量定义为W=[w1,w2,…,wN], 则任务执行优先级的计算方式为
(17)
1.5 目标函数
本文主要以车辆处理任务的总时延和MEC服务器计算资源服务费来衡量整个系统的性能,因此系统的目标函数为可定义为任务处理时延和MEC服务器计算资源服务费的加权和,如式(18)所示

(18)
在式(18)中,Fmax为单个MEC服务器最大计算能力。约束条件C1~C2表示卸载决策只有0和1两种取值且同一时刻只能取0或1;C3~C4表示MEC服务器为对应车辆分配的计算资源需大于0且不能超过服务器的最大计算能力;C5表示车辆自身也拥有一定的计算资源;C6表示车辆计算任务的卸载需要保证服务质量和任务执行的连续性。
2 基于麻雀搜索算法的计算卸载策略
问题Q1为混合整数非线性规划(mixed-integer nonli-near programming,MINLP)问题[19],应用穷举法可以获得此问题的最优解,但是穷举法将遍历所有可能结果,因此计算量较大会造成较高的延时,并不适合用于对实时性要求较高的车联网场景中。因此,本文提出一种基于麻雀搜索算法的计算卸载算法(computing offloading based on sparrow search algorithm,COSSA)来解决该问题。麻雀搜索算法(sparrow search algorithm,SSA)算法是模拟麻雀的觅食和反捕食行为的一种生物启发式算法,与灰狼算法(grey wolf optimizer,GWO)、粒子群算法(particle swarm optimization,PSO)等启发式算法相比,SSA具有良好的全局搜索能力,且收敛速度较快,可以有效的避免陷入局部最优值等优点[20]。
2.1 编 码
在式(3)中,卸载决策矩阵X (t) 被定义为只有0或1两种取值的离散变量,为了适应SSA的更新策略,本文对X (t) 进行整数编码。具体方式为:把X (t) 中的每一行看成二进制数然后转换成十进制整数,则t时刻车辆i的卸载决策由一个二进制向量编码为一个整数xi, 则编码后的卸载决策向量可定义为
X(t)=[x1(t),…,xi(t),…,xN(t)],i∈N
(19)
其中, xi是根据卸载决策矩阵X (t) 中的行向量计算而来,计算方式为
(20)
以M=2,N=3的场景中卸载决策的编码为例来说明上述编码过程,假设卸载决策矩阵见表1。

表1 卸载决策矩阵
表1所示的卸载决策矩阵的含义为:第1辆车卸载至编号为1的MEC服务器;第2辆车卸载至编号为2的MEC服务器;第3辆车为本地处理。则根据式(21),该卸载决策矩阵可编码为:X(t)=[2,1,4]。
2.2 适应度函数
系统的优化目标是最小化车辆处理任务的总时延和MEC服务器计算资源费用,则麻雀种群的适应度值可表示为
(21)
2.3 COSSA算法流程
在SSA算法中,麻雀初始种群位置定义为Sn=(sn1,sn2,…,snd), 其中n表示种群中麻雀的数量,d表示变量的维度其值为X(t) 的维度即:d=N。 则第n只麻雀的适应度值为fn=f(sn1,sn2,…,snd)。 根据麻雀的捕食习性,具有较高适应度值的麻雀(发现者)在搜索过程中会优先获得食物并且还会负责寻找食物和引导这个麻雀种群的移动方向,此外捕食者也将影响麻雀种群的移动方向[21]。则每次迭代期间,发现者的位置更新方式为
(22)
其中,g=[1,Itermax] 表示当前迭代次数,Itermax表示最大迭代次数。α∈(0,1] 是一个随机数,Alarm∈[0,1] 和Safe∈[0.5,1] 分别表示报警值和安全阈值。G是服从正态分布的随机数,V为1×d的单位向量。
对于加入者,他们会时刻监视发现者。当他们观察到发现者找到更好的食物,则加入者会立即朝着发现者的位置移动去获得食物,即加入者的位置更新方式为
(23)
其中,sopt和sworst分别表示发现者的最佳和最差的位置,A为一个1×d矩阵,且A+=AT(AAT)-1,NP表示麻雀总的种群数量。
对于整个麻雀种群,种群边缘的麻雀在意识到危险时迅速向安全区域移动以获得更好的位置,而处于群体中间的麻雀为了缩小危险范围而靠近其它麻雀进行随机游走。因此,麻雀种群位置更新方式为
(24)

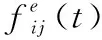
算法1:基于麻雀搜索算法的计算卸载算法(COSSA)

输出:最优卸载决策X*(t), 适应度值fglobal
(1) 随机初始化Np个卸载决策矩阵X(t);
(2) 把每个X (t)根据式(20)编码为卸载决策向量X(t) 组成麻雀种群Sn;
(3) 用式(21)计算适应度值fn, 并找出最小的适应度值fmin;

(5)whileg

(7)Safe=1;

(9) 用式(22)更新麻雀的位置;
(10)endfor

(12) 用式(23)更新麻雀的位置;
(13)endfor
(14)forn=1:Ns
(15) 用式(24)更新麻雀的位置;
(16)endfor
(17)iffglobal>fmin
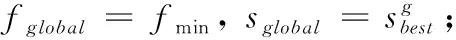
(19)endif
(20)g=g+1;
(21)endwhile
(22) 把sglobal解码为最优卸载决策X*(t);
3 仿真分析
为验证COSSA算法的优越性能,本文采用与文献[13]和文献[23]相同的方式做验证。此外,为验证COSSA算法良好的收敛性能,还将其与粒子群优化算法和灰狼优化算法进行对比。因此本文将COSSA算法与如下策略做比较:
(1)ALP:所有计算任务在车辆本地处理;
(2)AOMP:所有计算任务都卸载到同一个MEC服务器处理;
(3)Random:所有车辆的计算任务随机选择卸载至MEC服务器或在本地处理;
(4) COPSO:基于麻雀搜索算法的计算卸载策略,目标函数及编码方式与COSSA相同;
(5) COGWO:基于灰狼优化算法的计算卸载策略,目标函数及编码方式与COSSA相同。
参数设置主要参考文献[13]和文献[23],见表2。

表2 仿真参数
图2把COSSA与COPSO和COGWO算法相比较,3种算法均用相同的适应度函数和编码方式,最大迭代次数Itermax=1000。 从图2中可以看出,在有限的迭代次数内COSSA算法经过180次迭代后找出了全局最优值,而COGWO和COPSO算法要分别经过400和220次迭代才能收敛。此外,COPSO算法易陷入局部最优值,其相较于COSSA算法目标函数值较大,使得系统开销也较大;COGWO的目标函数值与COSSA算法最为接近,但其收敛较慢。因此,COSSA算法的收敛性能优于COPSO和COGWO算法,在收敛速度方面分别提升了18%和45%。
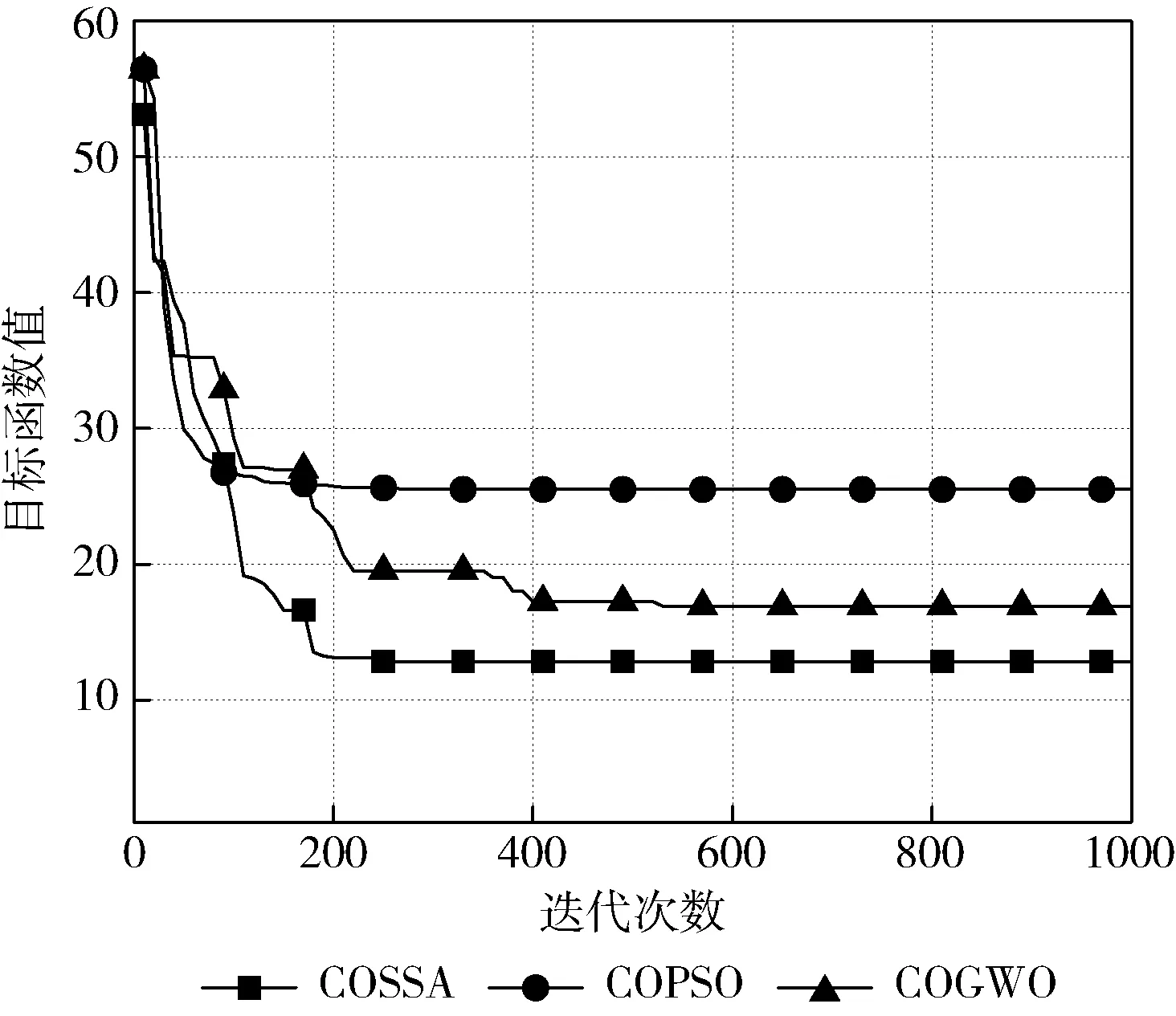
图2 算法收敛性分析
图3为车辆数在[10,50]范围内变化时,车辆数与系统效用值之间的关系。随着车辆数的增加,系统效用值也在不断增长,这是因为车辆数目的增加必然导致任务处理总时延和资源服务费增加,从而使得系统效用变大。从图3中可以看出,当车辆数小于30时,4种卸载策略无明显差别,当车辆数大于30时,ALP、AOMP和Random策略的效用值急剧增长,而COSSA策略在车辆数较多时仍能保持较低的系统效用,实现了最优的效果。

图3 车辆数与系统效用的关系
图4为车辆数与系统中车辆任务处理总时延之间的关系。随着车辆数的增加,4种策略的任务处理总时延差距越来越大,这说明不同的策略将对VEC系统的任务执行时延产生影响。其中,Random策略是随机选择将计算任务卸载至MEC服务器或本地处理,因此其效果最差;而COSSA策略同时考虑了任务执行时延、MEC服务器负载均衡以及任务执行的连续性,因此COSSA策略始终保持最低的任务处理时延,有效地提升了用户体验,实现了最佳性能。

图4 任务完成时延对比
图5展示了车辆数为20,任务数据量在[50,100]kb范围内变化时,任务数据量与系统效用值之间的关系。如图5所示,随着任务数据量的增加,系统效用也在不断增加。这是因为车辆和MEC服务器的计算资源一定时,任务数据量增加直接导致任务处理、传输时延以及资源使用费的增加,从而使得系统效用变大。其中,由于车辆计算能力较弱,任务数据量增多导致处理时延较长,因此ALP策略效果较差,而COSSA策略始终保持较低的系统效用,实现了车载终端与MEC服务器的负载均衡。
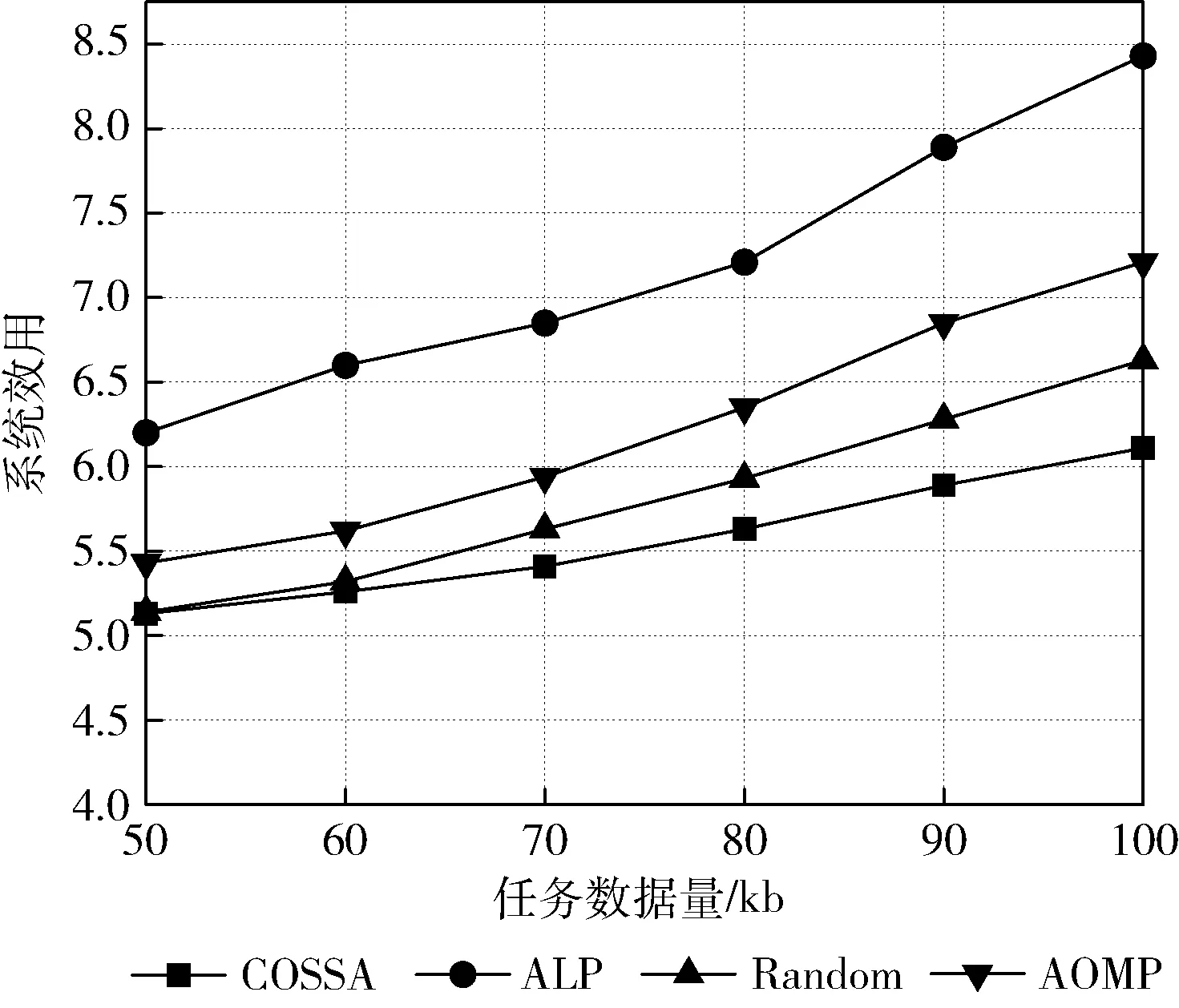
图5 任务数据量与系统效用的关系
4 结束语
针对车联网场景下的边缘计算系统中MEC服务器负载不均衡,紧急任务无法得到优先处理的问题,提出一种COSSA策略。首先利用层次分析法根据任务的属性为每个需要卸载任务分配优先级,然后利用麻雀搜索算法根据目标函数找出最优的卸载决策,以最小化系统效用,实现服务器负载均衡。实验结果表明,COSSA与COPSO和COGWO策略相比具有更好的收敛性能。与Random、ALP和OMP策略相比,COSSA策略可以有效地降低系统开销、均衡MEC服务器负载。下一步将对VEC系统中车辆移动性管理以及车辆计算任务的部分卸载问题进行深入研究。

