交叉口多车串联掉头几何设计与信号配时优化

宋 浪， 白明举， 叶 青， 王少飞， 安文娟

(1.招商局重庆交通科研设计院有限公司， 重庆 400067； 2.贵州省都匀公路管理局， 贵州 都匀 558000)

城市中心城区部分道路中央分隔带较窄，再加上禁止左转、支路右进右出等快速化通行处置措施，导致车辆掉头问题较为突出。常见的掉头设计模式有路口掉头、掉头车道右置掉头、停止线前掉头、导向车道上游掉头等[1]。杜志强[2]分析了北京信号交叉口左转和掉头车辆的车头时距特性，为掉头车道的设置提供了理论支持。张小龙等[3]研究了车辆提前掉头几何参数设置，给出了设置提前掉头的阈值流量。王宇轩[4]探讨了交叉口掉头车道的几何设计条件，提出了中央分隔带车辆掉头开口长度计算模型。刘骏等[5]则对掉头车道右置的安全性进行了分析。王振等[6]提出了借用BRT车道掉头的控制方法。车辆一般在交叉口进行掉头，由于车辆掉头对转弯半径、道路坡度等几何条件要求较高，受城市地形条件限制，若中央分隔带宽度较窄，在交叉口设置掉头车道易降低车辆通行效率。

为避免左转和直行冲突对交叉口通行效率的影响，部分学者对中位U型回转、限制交叉U型回转等开展研究，U型回转与借道左转[7]、排阵式交叉口[8]、连续流交叉口[9]、平行流交叉口[10]等皆属于非常规交叉口设计。交叉口采用U型回转设计，能够降低支路车辆对主线交通的干扰，提升交叉口车辆通行效率。Combinido等[11]建立了U型回转掉头车辆的交通流模型。而Al-Obaedi等[12]建立了U型回转的通行能力模型。张卫华、Che、Hustim等[13-15]分别针对U型回转的几何设计、运行速度、交通噪声进行了研究。

城市日常出行及设置U型回转等，均会产生交叉口掉头需求。然而根据杜志强[2]对北京6个道路坡度为零的信号交叉口调查发现，左转和掉头车辆放行时的饱和车头时距平均值分别为2.15 s、4.93 s，表明左转车道饱和流率约为掉头车道的2.29倍，即在相同绿灯时长下左转车道通行能力约为掉头车道的2.29倍。对于山区城市道路，受道路坡度等影响，掉头饱和车头时距会更大，从而导致掉头通行能力严重不足。为此，重庆市交警部门首次创新推出了多车串联掉头的非常规交叉口设计，并在市内选择小龙坎正街—天陈路、石小路—黄桷园小区出口、凤天大道—凤怡路、盛德路—景辉路等4处交叉口进行试点实施，已于2022年1月试运行，与传统的常规掉头设计相比，实际应用效果良好。

鉴于目前多车串联掉头设计的研究成果极少，为使多车串联掉头设计更符合实际交通运行需要，本文以多车串联掉头设计为研究对象，探讨其几何设计条件和信号控制策略，以提升交叉口通行效率。

1 多车串联掉头几何设计方法

多车串联掉头几何设计如图1所示。在掉头车道上设置多个待行车位，并利用数字编号进行待行车位标记(1～4)，同时将待行车位范围内的中分带车行道分界线施划虚实线，以便允许掉头车辆驶入对向车道。上游到来的掉头车辆依次进入待行车位1～4，然后根据信号灯指示同时掉头。在交叉口常规掉头设计中掉头车道饱和车头时距约为左转车道的2.29倍[2]，原因是受道路条件限制，掉头车辆一般以最小转弯半径进行掉头，使得车辆掉头运行速度较低，导致通行能力下降。若道路存在一定坡度，或掉头车道距最外侧出口车道间距过小，导致车辆在掉头过程中需要倒车来调整车辆姿态才能完成掉头，均会进一步导致掉头通行能力下降。因此，由于常规掉头设计通行效率较低，而多车串联掉头设计允许多辆车同时掉头，则提升了掉头通行效率。

图1 多车串联掉头几何设计Fig.1 Geometric design of multi-vehicle tandem U-turn

参考王宇轩[4]和《城市道路工程设计规范》(CJJ 37—2012)，给出掉头车辆运行轨迹宽度计算公式：

(1)

式中：βt为车辆掉头运行轨迹宽度，m；l为车辆在掉头车道上内侧距中分带中线的距离，m；aw为车辆宽度，m；agc为车辆轴距加前悬的距离，m；R为车辆掉头半径，m；v为车辆掉头运行速度，km/h。

车辆横向安全距离采用经典的波良可夫经验模型[16]计算，如下式：

(2)

式中：δ1为2股车流对向行驶横向安全距离，m；δ2为2股车流同向行驶横向安全距离，m；δ3为车流与路缘石的横向安全距离，m；v′为对向行驶车流运行速度，km/h。

多车串联掉头设计中待行车位长度要满足掉头运行轨迹需要，且相互间不存在干扰，故待行车位长度由掉头车辆运行轨迹宽度、横向安全距离和掉头起始位置长度组成，计算如下：

Wmk=βt+2δ3+ask=1

(3)

(4)

(5)

式中：Wm为中分带开口总长度，m；Wmψ为第ψ个待行车位长度，m；ψ为待行车位顺序编号，以距停车线最近的待行车位开始编号，一共k个待行车位；as为掉头车辆起始位置长度，m。驾驶员启动车辆后并不会立即掉头，而是往前行驶调整车辆姿态以便选择掉头的起始位置。

城市道路交叉口中具有掉头需求的车辆一般为小客车，故本文仅考虑小客车掉头。《城市道路工程设计规范》(CJJ 37—2012)规定小客车车辆宽度1.8 m，轴距加前悬4.6 m。据王宇轩[4]的现场调查结果显示，掉头车辆起始位置长度宜取为2.6 m，车辆实现掉头的整个过程中运行速度始终不超过10 km/h。采用式(1)～式(5)计算中分带开口长度，如图2所示。图2(a)首待行车位和末待行车位变化曲线重合。由图2可知，待行车位长度、多车串联掉头总长度随掉头车辆内侧距中分带中线距离的增加而减小，一般情况下掉头车辆内侧距中分带中线距离超过2 m，所以单个待行车位长度可设置为6 m～7 m。

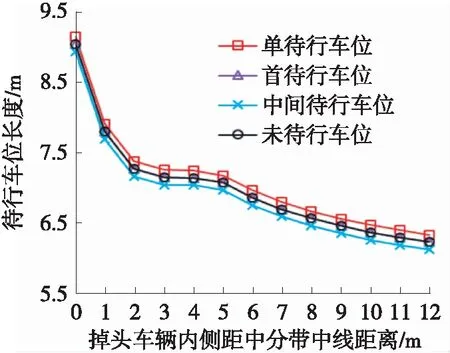
(a) 单个待行车位长度

2 多车串联掉头交通特性分析

2.1 信号相位方案设计

多车串联掉头设计在信号控制交叉口的应用中，左转、直行和右转相位与常规交叉口相同，右转可根据是否设置右转专用道来选择红灯右转或绿灯右转，如图3所示。为避免交通冲突，掉头车辆在红灯右转控制方式中可选择与本道路左转和相交道路直行同相位放行，但与红灯右转车辆存在干扰，在绿灯右转控制方式中可选择与本道路左转同相位放行。由于多车串联掉头在整个中分带开口区域均会有车辆掉头，所以在掉头相位绿灯启亮前，此开口区域出口侧车道应清空，故掉头相位绿灯应相对于左转相位绿灯迟起。

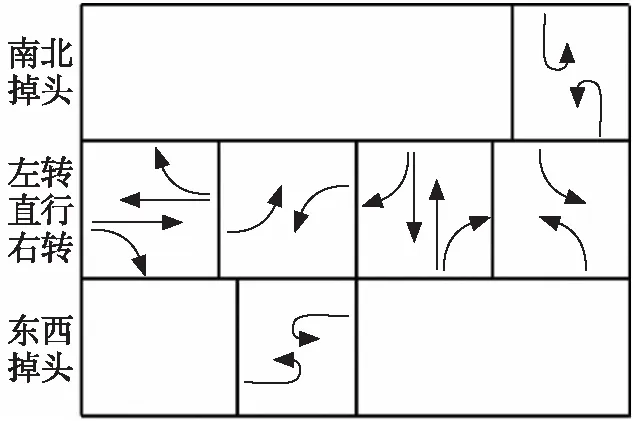
(b) 绿灯右转图3 信号控制相位方案Fig.3 Scheme of signal control phase

由图3(b)可知，在绿灯右转控制方式中，十字交叉口的掉头相位绿灯时长不超过左转相位，结合杜志强[2]调查的两者饱和车头时距关系，可得到常规掉头车道通行能力不足左转车道的一半。而对于T型交叉口，不管右转采用何种控制方式，上述通行能力关系始终成立。

2.2 多车串联掉头车道饱和流率修正

根据多车串联掉头设计的车辆运行规则可知，多辆车同时掉头所需时间由跟车进入待行车位时间加上掉头过程消耗时间组成，如下式：

hφ=(φ-1)hf+hU∀φ

(6)

式中：hφ为φ辆车同时掉头的饱和车头时距，s；hf为每辆车跟车饱和车头时距，s/pcu；hU为每辆车掉头饱和车头时距，s/pcu；φ为同时使用待行车位的掉头车辆数量。

受驾驶员是否熟悉多车串联掉头设计及自身驾驶习惯等因素的影响，对于设置有k个待行车位的掉头车道，每次同时使用的待行车位数量可能达不到k值，由此计算平均车头时距为：

(7)

(8)

式中：h为多车串联掉头设计中平均每辆车的车头时距，s/pcu；pφ为φ辆车同时使用待行车位掉头的概率。

根据上述分析可知，多车串联掉头设计提升了掉头车道通行能力，有效缓解了交叉口拥堵，但由于运行规则较为复杂，驾驶员可能存在一定困惑，造成待行车位利用率不高，故需配套建设相应标志标线及运营初期安排交警现场引导，以帮助驾驶员熟悉多车串联掉头设计运行规则。

3 多车串联掉头信号配时优化模型

选择十字交叉口为研究对象，信号控制相位方案采用图3(b)方案，以此构建优化模型。

3.1 目标函数

考虑延误可被驾驶员直观感受到，故本文以交叉口车均延误最小化作为目标函数，如下式：

(9)

式中：d为交叉口车均延误，s；qij为i进口j转向流量，pcu/h；dij为i进口j转向车均延误，s；i为车流到来方向，i∈{1,2,3,4}分别表示西、南、东和北；j为交叉口转向，j∈{1,2,3,4}分别表示掉头、左转、直行和右转。

采用经典的Webster模型[17-19]计算延误，如下式：

(10)

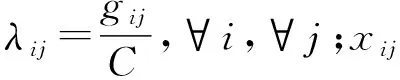
3.2 约束条件

1) 一般控制约束

结合图3(b)相位方案可知，同相位放行车流绿灯时长应相等，如式(11)、式(12)。周期时长与各相位绿灯时长存在一定关系，如式(13)。周期时长、绿灯时长应在合理的范围内，同时也要考虑行人过街需求[20]，如式(14)～式(16)。

gij=g(i+2)ji=1,2j=2,3,4

(11)

gij=gi(j+1)∀ij=3

(12)

(13)

Cmin≤C≤Cmax

(14)

gmin≤gij≤gmax∀i∀j

(15)

(16)

式中：I为绿灯间隔时间，s；Cmin、Cmax分别为周期时长最小值、最大值，s；gmin、gmax分别为绿灯时长最小值、最大值，s；Lpi为i进口直行车流放行时所对应放行的行人流过街人行横道长度，m；vpi为i进口直行车流放行时所对应放行的行人流过街速度，m/s。

2) 掉头控制约束

引入0-1变量来判断掉头车道设置的待行车位数量是否为k，以便整合到一个统一的优化模型中。结合图3(b)相位方案和多车串联掉头设计运行规则可知，掉头与左转相位差为式(17)，则掉头相位绿灯时长为式(18)。掉头车道饱和流率采用式(19)计算。式(20)～式(21)为0-1变量约束条件。

(17)

(18)

(19)

(20)

δik∈{0,1} ∀i

(21)

3) 饱和度约束

为避免某转向存在过饱和现象，故饱和度应存在最大值约束。

(22)

式中：Ymax为饱和度最大值，s。

3.3 模型求解

所构建的优化模型为包含绿灯时长gij、待行车位设置数量判断变量δik等2类决策变量的0-1混合整数非线性规划模型，在设计阶段可根据道路几何条件及交通组成等约束，通过枚举法一一枚举δik值，将其转换为非线性规划模型以便于求解。在运营阶段δik已为定值，优化模型为包含绿灯时长gij决策变量的非线性规划模型。多数求解器均可求解非线性规划问题。

4 案例分析

4.1 基础参数

选择十字交叉口为案例对象以对比多车串联掉头设计与常规掉头设计(待行车位数为1个)的运行性能。设计8种流量方案进行对比分析，如表1所示，其中高流量方案均为低流量方案的1.5倍，同时令4个进口几何设计与交通组成相同，以便更直观比较两者的通行效率。基础参数取值：掉头车道数1条、左转车道数1条、直行和直右车道数1条、驶离车辆运行速度25 km/h、绿灯间隔时间4 s、饱和度最大值0.85、行人速度1 m/s。令l=2 m确定中分带开口总长度，将待行车位数取值为1～10个，以分析待行车位数对车均延误的影响。

表1 流量输入方案 pcu/hTable 1 Traffic volume input scheme

4.2 结果分析

采用本文所构建的优化模型进行信号配时，车均延误结果如图4所示。由式(6)可知，掉头车道饱和流率随待行车位数的增加而增加，而据式(17)可知，待行车位数的增加会导致中分带开口长度增加，从而使出口侧车道清空时长增加，进而降低掉头有效绿灯时长。因掉头通行能力与饱和流率、有效绿灯时长均呈正相关，所以待行车位数的增加导致掉头通行能力先减后增，同时也使得车均延误随待行车位数的增加呈先减后增的变化趋势。随着掉头流量的增加，在待行车位数过小或过大时，均可能出现掉头通行能力不满足交通需求的情况，如方案6和方案8。最佳待行车位数量与交通组成、掉头车道饱和流率等密切相关。

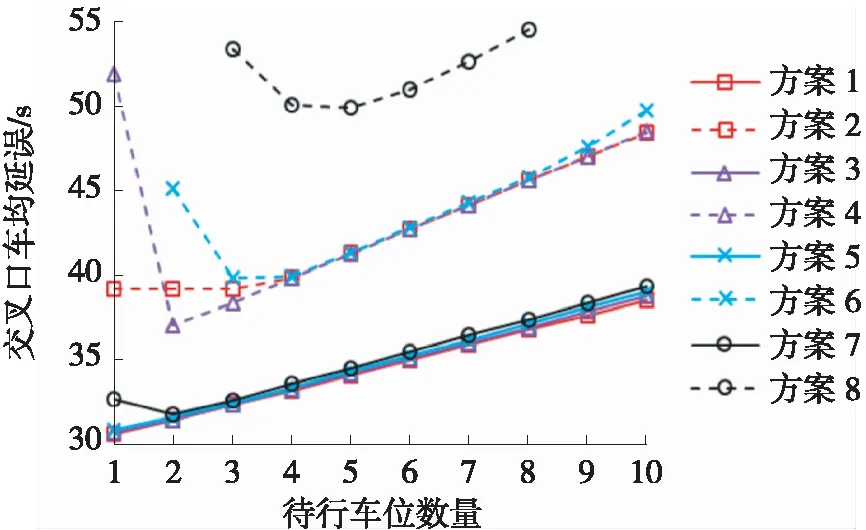
(a) 交叉口车均延误

(b) 掉头车均延误图4 车均延误对比分析Fig.4 Comparative analysis of average vehicle delays

5 结束语

1) 为解决城市交叉口掉头通行能力不足的问题，提出了多车串联掉头几何设计方法，并给出掉头车辆运行规则。从掉头车辆运行轨迹宽度、横向安全距离和掉头起始位置长度等建立待行车位长度计算模型，结果发现待行车位长度随掉头车辆内侧距中分带中线距离的增加而减小，单个待行车位长度可设置为6 m～7 m。

2) 分析了多车串联掉头设计的交通特性，进而修正多车串联掉头车道的饱和流率计算公式，并建立信号配时优化模型。案例分析结果显示，车均延误随待行车位数的增加呈先减后增的变化趋势，采用多车串联掉头设计相较常规掉头设计，有效提升了掉头车道的通行效率。

3) 本文仅探讨了多车串联掉头设计在交叉口的应用，后续可进一步推广到左转掉头共用车道、导向车道上游掉头、道路路段上及U-turn等设计中。