一种改进的基于多接收机协同SAR欺骗干扰方法

刘业民，吕汉峰，袁露，刘晓娴，冷文

（1.中国人民解放军第32579部队，广西 桂林 541001；2.中国人民解放军第93209部队，北京 100085）

0 引言

合成孔径雷达（SAR）具有全天时、全天候、作用距离远、分辨成像高等优点，其在民用和军事领域得到了广泛的应用［1］。随着SAR在军事领域（如战场侦察、精确制导以及地面运动目标检测等）中作用发挥日益显著，针对SAR的对抗技术也引起了世界军事强国和雷达界的重点关注。对SAR欺骗干扰作为SAR对抗的一个重要发展方向，由于具有干扰功率低、灵活性强、逼真度高等优点，已成为目前雷达电子战研究的热点和难点问题［2-8］。

对SAR欺骗干扰的效果好坏取决于对SAR系统一些关键参数侦察精度的高低，如SAR载机平台速度、斜视角以及干扰机到SAR载机平台的最近斜距等，对SAR欺骗干扰的传统方法通常假设这些关键参数已预先侦察好，且不存在误差。然而在实际应用中，这些侦察参数通常需要复杂的侦察设备来辅助完成，且估计参数误差是不可避免的。为此，针对欺骗干扰过程中SAR系统参数侦察精度不高或侦察参数不完备的难题，一些学者提出了一种基于多接收机协同的SAR欺骗干扰方法［9］。该方法利用干扰机和接收机的布站以及接收机间的到达时差（TDOA）信息，有效地解决了需复杂设备侦察关键参数的难题，大大简化了干扰系统的配置。然而，文献［9］方法仍然有以下几点需要进一步完善：1）对侦察到的SAR参数没有明确其物理含义，因而没有充分挖掘出并用好这些参数；2）相位补偿精度还不够高，导致虚假目标峰值位置偏移量随着生成的虚假目标离干扰机距离增大而增大，且目标聚焦效果也略微变差；3）对SAR的欺骗干扰算法中涉及到卷积，其干扰实时性有待改进。

基于上述背景和问题，本文提出了一种改进的基于多接收机协同SAR欺骗干扰方法。相比于文献［9］方法，该方法主要有2个创新点：1）明确了基于多接收机的协同侦察参数的物理含义，根据参数物理含义可实现对SAR载机平台的无源测向；2）随着生成的虚假目标离干扰机距离增大，该方法比文献［9］所提方法生成的虚假目标峰值位置和聚焦效果要好，且干扰算法比现有方法实时性强。本文首先阐述了多接收机协同干扰原理；在此基础上，对侦察参数进行了详细分析；然后给出了一种对SAR欺骗干扰精度高和实时性强的干扰算法；最后通过仿真实验对文献［9］方法和所提方法的干扰效果和干扰实时性进行了对比分析。

1 多接收机协同干扰原理

首先回顾基于多接收机的协同干扰原理。如图1所示，假设SAR工作在条带模式，SAR载机平台以速度va沿直线匀速运动，载机高度为H，以SAR载机平台飞行方向为x轴的正方向，垂直于x轴在地面投影为y轴正方向建立右手直角坐标系Oxyz，原 点O为当方位向慢时间ta=0时，SAR载机平台在地面上的投影点，点O′为SAR条带中心线与y轴的交点，且OO′=Y。在条带区域内放置一部干扰机，其坐标为(RJtanθc，Y，0)，其 中RJ=(Y2+H2)1/2为干扰机到SAR载机平台的最近斜距，θc为斜视角。

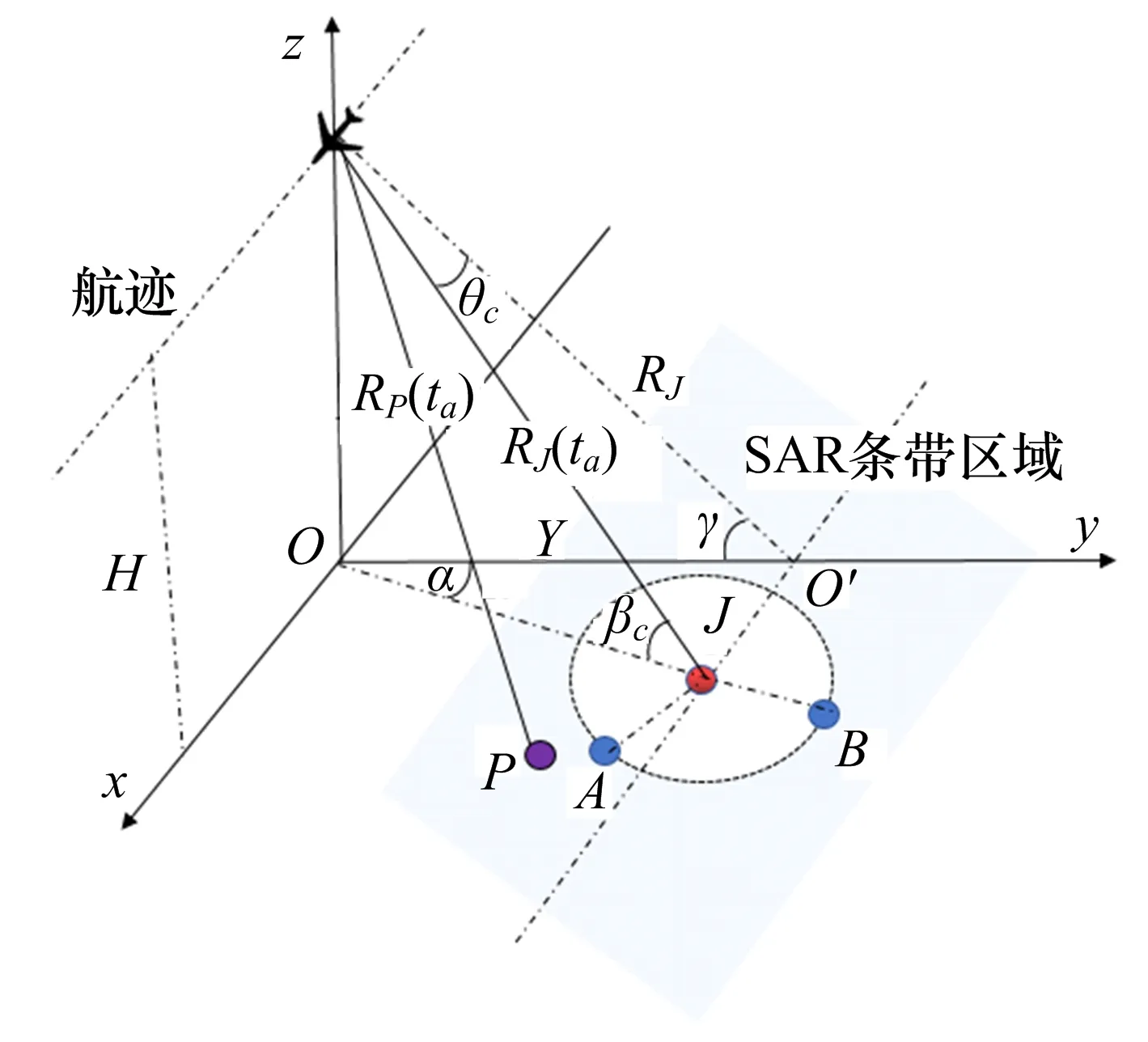
图1 多接收机协同干扰几何关系图

若有点目标P位于坐标(xP，yP，0)处，且SAR载机平台到点目标P的瞬时斜距为RP(ta)，假设SAR发射的信号为线性调频信号，则SAR接收到目标P的回波信号可表示为（经下变频处理）：

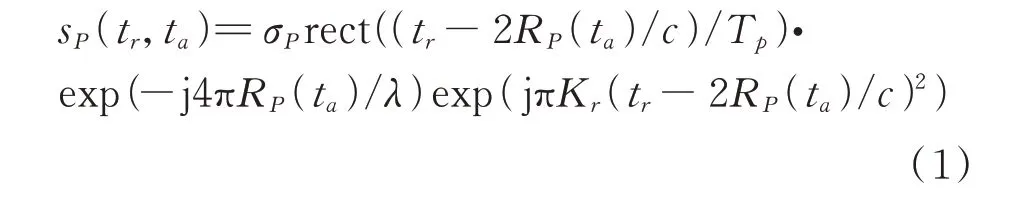
式中，σP为目标P的后向散射系数，rect(·)为矩形窗函数，Tp为发射信号脉宽，λ为信号波长，Kr为线性调频率，tr为距离向快时间，c为光速。

当SAR波束照射到干扰机时刻，干扰机开始截获SAR信号并调制信号，若位P处需生成一个虚假目标，则转发的欺骗干扰信号形式为［9］：

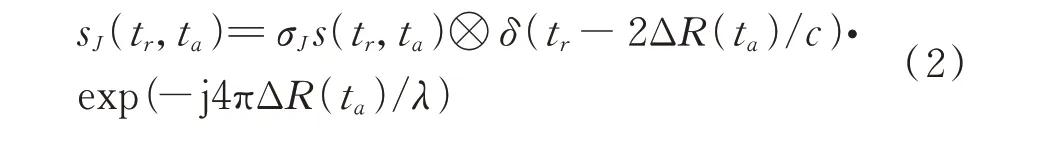
式中，σJ为干扰信号幅度大小，s(tr，ta)为干扰机截获的SAR信号，δ(·)为冲击函数，符号“⊗”表示卷积运算符，ΔR(ta)=RP(ta)-RJ(ta)，RJ(ta)为SAR载机平台到干扰机J的瞬时斜距。

为计算出ΔR(ta)，令RP(ta)和RJ(ta)的空间矢量分别为rP和rJ，其距离大小分别为‖rP‖2和‖rJ‖2，其中符号‖·‖2表示欧几里德范数操作符。在远场假设的条件下，SAR发射的信号可看作平面波，即不同散射点的波束彼此平行，此时有rP||rJ，符号||表示“平行于”。若Δr和r′Δ分别表示干扰机J到点目标P的空间矢量和该矢量在矢量rJ上的投影，则ΔR(ta)可计算出［9］：

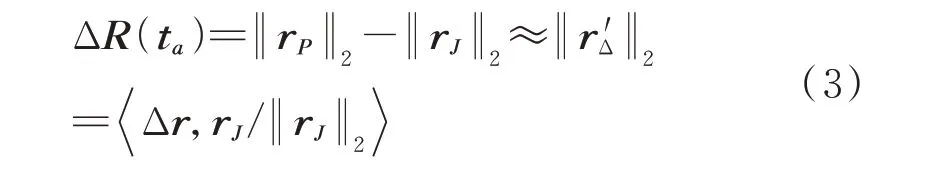
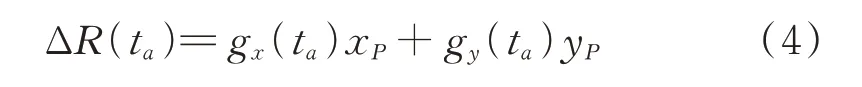
式中，

βc为干扰机相对于SAR载机平台的俯仰角。

由式（4）可知，相对于干扰机而言，点目标P的位置是已知的，而gx(ta)和gy(ta)是未知的。为获得这2个未知量，文献［9］提出可利用干扰机与接收机以及接收机间的TDOA信息来求解。如图1所示，以干扰机为中心，以rJ为半径的圆上布放了2部接收机，分别位 于 图 中A点 和B点，其 坐 标 分 别 为(xA，yA，0)和(xB，yB，0)。若每台接收机均与干扰机通过有线连接方式实现通信功能，则根据式（4），有：

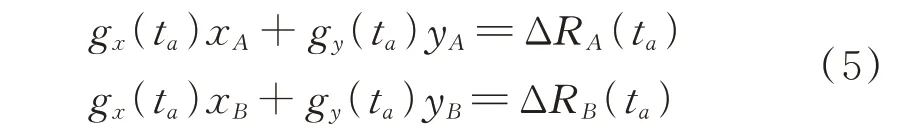
式中，ΔRA(ta)和ΔRB(ta)可由接收机A和接收机B到干扰机的TDOA获得。通过式（5）可求出gx(ta)和gy(ta)，将其代入式（4），根据式（2），最终可实现对SAR的欺骗干扰。

2 侦察参数分析

在第1节的基础上，本节主要解决引言部分提及文献［9］方法中第一点需要改进的地方。由式（4）可知，文献［9］方法中在实施欺骗干扰时，gx(ta)和gy(ta)是作为一个整体进行处理的，事实上，这两个参数有其明确的物理含义。为此，假设SAR照射条带区域中任意点目标的坐标为(x，y，0)，则该点目标到SAR载机平台的瞬时斜距可看作是关于x和y的函数，即：

式 中，xs=Rtanθc，R为点目标到SAR载机平台的最近斜距。

为揭示侦察参数的物理含义，假设位于条带区域内干扰机的坐标为(xJ，yJ，0)，根据泰勒公式定义［10］，则式（6）在x=xJ和y=yJ处的二元泰勒级数展宽式为（保留至二次项）：

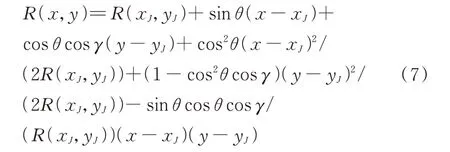
式 中，sinθ=-(vata-xs-xJ)/(R(xJ，yJ))，cosγ=(Y+yJ)/RJ。式（7）中最后三项为泰勒级数的二次项和交叉项，研究表明，它们值远远小于前三项，由于受测量误差影响较大，因此不考虑直接参与计算。记ΔR(ta)=R(x，y)-R(xJ，yJ)，则式（7）可简化为：

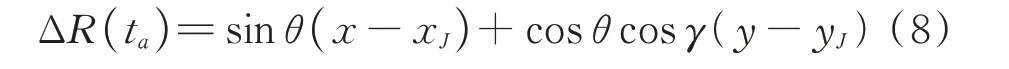
通过对比式（4）和式（8）不难发现，式（4）是式（8）的一种特殊情况，即当xJ=0和yJ=0时，式（8）退化成式（4）。由sinθ表达式可知，角度θ表示瞬时斜视角，角度γ为干扰机最近斜距与y轴的夹角，如图1所示。此外，根据图1的几何关系，线段OJ与y轴的夹角α可通过角度θ和γ来表示，即有：

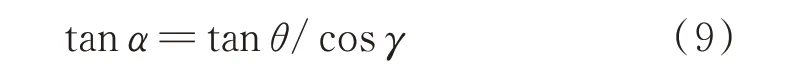
干扰机相对于SAR载机平台的瞬时俯仰角β也可通过角度θ和γ来表示，即有：

根据角度α和β信息，可求得在主瓣波束照射2部接收机期间内干扰机相对于SAR载机平台的水平方位角和俯仰角，其值大小分别为(π/2-α)和β。通过这些角度信息，可实现对SAR载机平台的无源测向，这为干扰机对SAR实施干扰提供了干扰方位基准。

3 欺骗干扰算法

本节给出一种对SAR的欺骗干扰算法，主要解决引言部分提及文献［9］方法中后面两点需要改进的地方。研究表明，式（7）中的后三项可补偿虚假目标所在位置与干扰机所在位置的调频斜率差以及改善虚假目标峰值的位置。因此，为提高干扰的逼真度，在实施干扰时，需将式（7）中的后三项考虑其内。在式（7）中，参数R(x，y)是未知的，根据第2节获得的侦察参数，可推导出干扰参数R(x，y)。假设SAR载机平台的飞行高度H是已知的，高度H比起干扰机到SAR载机平台的斜距而言，通常更容易获得。尤其是对于星载SAR平台而言，其飞行轨道高度通常是固定的。为此，根据角度β和高度H信息，可估计出干扰机到SAR载机平台的瞬时斜距为：

将式（11）代入式（7），那么估计的斜距差可表示为：

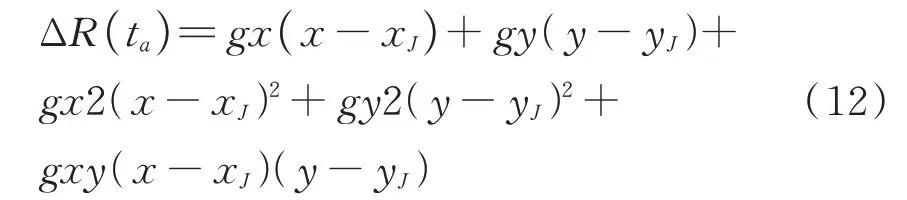
式中，

gx和gy由式（8）求得，然后通过角度θ和γ以及式（11）中的(xJ，yJ)，可分别求得gx2、gy2以及gxy。

将式（12）代入式（2），即可对SAR实施欺骗干扰。由式（12）可知，虚假目标与干扰机在x轴和y轴上的差值(x-xJ)和(y-yJ)可根据干扰需求预先设定好，无需知道干扰机的具体位置信息。式（13）中的干扰参数可作为一个整体解算，可无需知道SAR载机平台速度、斜视角、慢时间以及干扰机方位向坐标等参数，从而简化了干扰系统对侦察参数的需求量。

为避免卷积运算，提高其干扰的实时性，可对式（2）在距离向作快速傅里叶变换（FFT）［11］，完成计算后，再作快速傅里叶逆变换（IFFT），即：

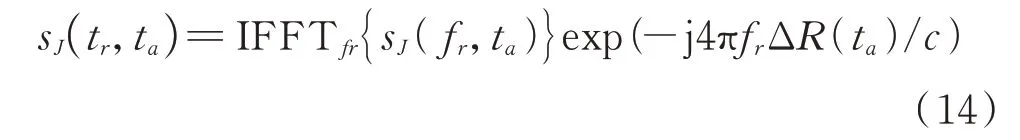
式中，sJ(fr，ta)为截获的干扰信号在距离向作FFT的结 果，IFFTfr{·}表 示IFFT操 作 符，fr=fc+fR，fc为SAR信号载频，fR为距离向频率。

综上所述，与传统SAR欺骗干扰方法相比，本文所提方法无需估计出SAR载机平台速度、慢时间、斜视角以及干扰机具体坐标位置等侦察参数。因此，所提方法比传统SAR欺骗干扰方法更简单实用，与文献［9］方法相比，进一步提高了斜距差ΔR(ta)的计算精度以及干扰实时性。

4 仿真实验验证与结果分析

在仿真实验中，假设SAR工作模式为条带模式，其系统仿真参数如表1所示。

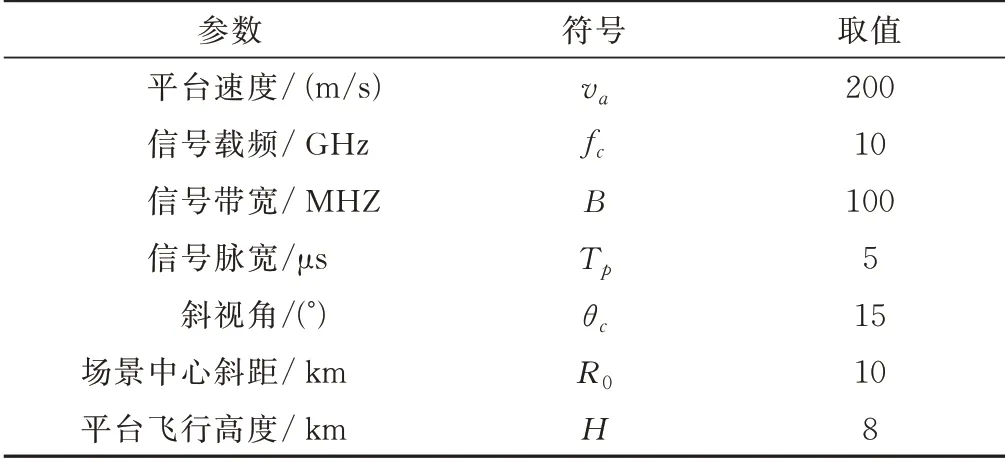
表1 SAR系统仿真参数

在仿真实验中为便于阐述，不妨设定干扰机的坐标位置为（0 m， 8 000 m， 0 m），以干扰机中心坐标为圆心，接收机部署在半径为20 m的圆上。根据最优布站要求［9］，不失一般性，接收机A和B的坐标分别可设定为（20 m， 8 000 m， 0 m）、（0 m， 8 020 m， 0 m）。在干扰场景中设定9个虚假静止目标，分别用P1～P9标识，相邻目标其距离向和方位向间距均为100 m，其位置分布如图2所示。图2中采用的是xOr空间坐标系，其与空间坐标系Oxyz的坐标转换关系为x=x，r=(y2+z2)1/2。

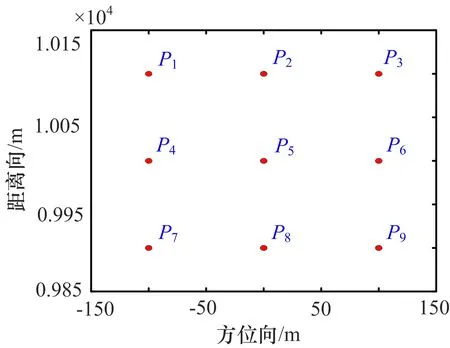
图2 场景目标位置设定示意图

分析本文所提方法的无源测向精度。图3给出了主瓣波束照射3部接收机期间内所提方法对SAR载机平台的无源测向性能，其中图3（a）为水平方位角(π/2-α)的测角性能，图3（b）为俯仰角β的测角性能。从图3可以看出，本文所提方法的测角精度与理论值吻合度很好。由于水平方位角是慢时间的函数，为此图4进一步给出了水平方位角的测角误差，横坐标是主瓣波束照射3部接收机期间内SAR载机平台水平方位角变化范围，纵坐标是水平方位角的均方根误差（RMSE），蒙特卡洛仿真次数为2 000次。由图4可知，当水平方位角逐渐变大，其水平方位角的RMSE亦变大（即测角性能逐渐变差），但水平方位角的RMSE总体变化均很小，平均值只有8.97×10-4rad。仿真实验验证了本文所提的无源测向方法可为干扰机对SAR实施干扰提供方位基准。

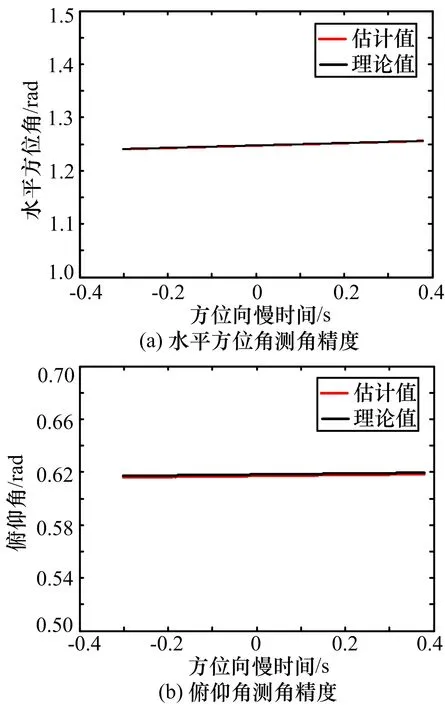
图3 无源测向精度分析

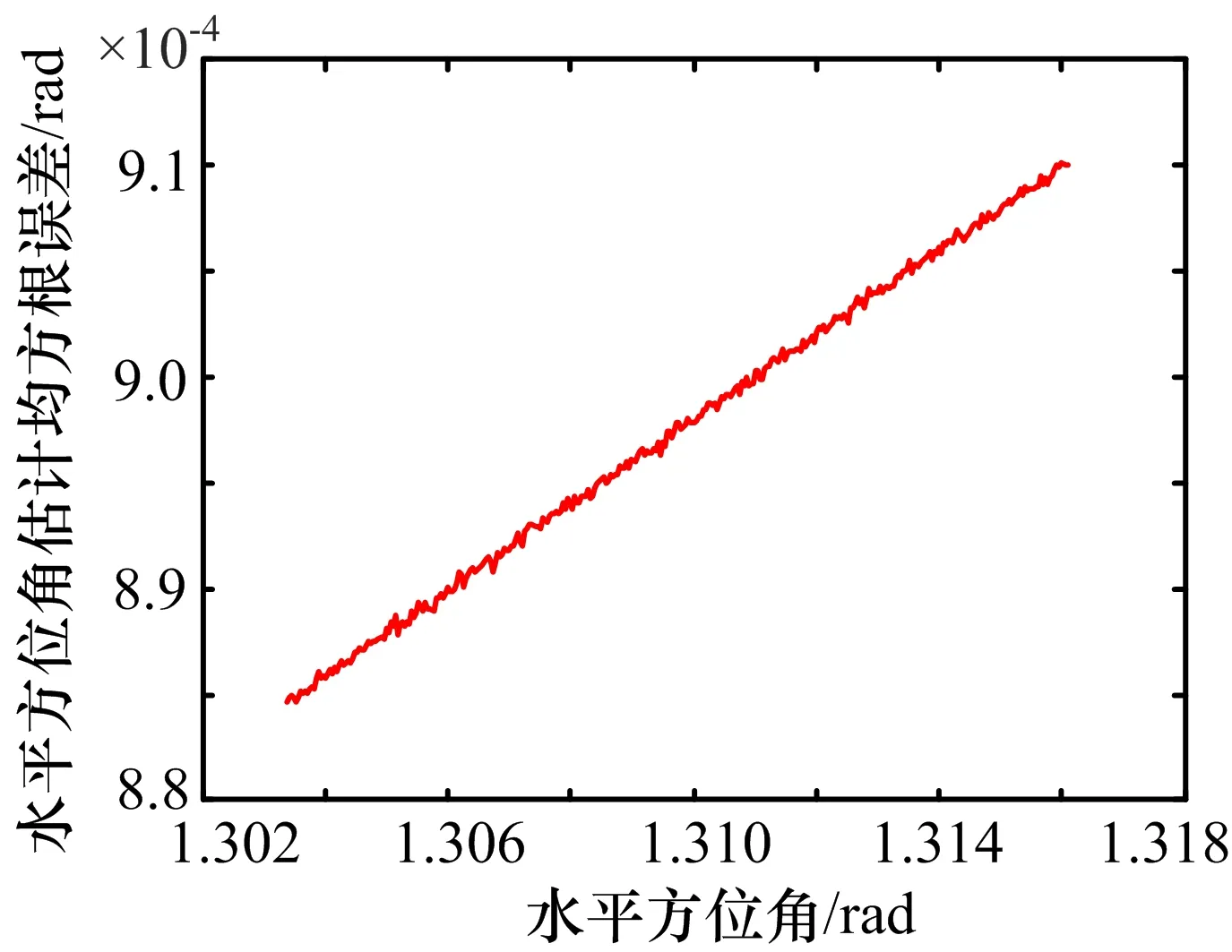
图4 水平方位角的RMSE

对比文献［9］方法和本文所提方法的成像效果。除第2节中因使用近似表达式会存在理论误差外，测量误差在实际应用中也必须考虑。为此，仿真中考虑了TDOA测量误差，该测量误差可模型化为零均值的高斯白噪声，其误差标准方差可设为1.5×10-4m［9］。按照图2的干扰场景设定，图5给出了本文所提方法生成9个虚假目标的二维成像结果图，从图中可以直观看出，所提方法中9个点目标均聚焦成像效果良好。

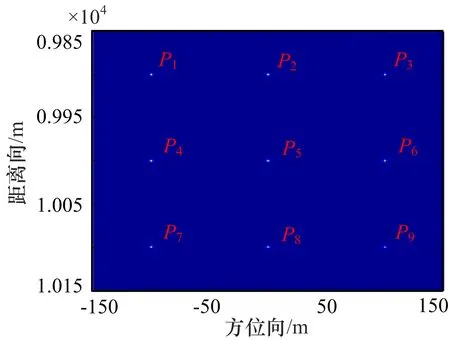
图5 虚假目标的二维成像结果

为了便于对比文献［9］方法和本文所提方法的聚焦成像效果，不失一般性，图6给出了目标1、目标5以及目标9的二维升采样成像图，并将真实目标、文献［9］方法以及本文所提方法生成的虚假目标作为对比。图7给出了真、假目标距离向和方位向的升采样剖面图。为简洁直观，图6和图7的纵坐标位置均与中心场景斜距R0作了差值处理（下同）。从图6和图7中容易看出，相比于真实目标，文献［9］方法和本文所提方法生成的虚假目标距离向聚焦效果跟真实目标几乎相当，而在方位向上虚假目标的主瓣均比真实目标略微展宽。此外，相比于所提方法，文献［9］方法中离干扰机较远的目标（如目标P1和P9），由于相位补偿精度不够高（式（7）的后三项在文献［9］方法中未补偿），导致虚假目标方位向和距离向峰值位置偏移量增大。

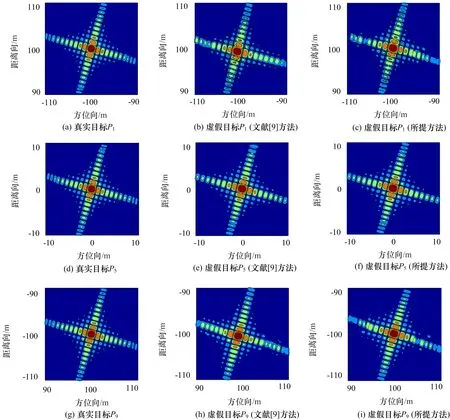
图6 目标升采样二维成像结果图

从上面分析可知，在虚假目标间隔干扰机较近的情况下，文献［9］方法和本文所提方法的成像效果相当。为进一步对比验证2种方法的成像聚焦性能，现考虑相邻2个目标在距离和方位向的间距均为150 m，9个点目标的分布情况同图2。同图5仿真条件，图8给出了真假目标1、目标5以及目标9升采样的二维成像图、距离向以及方位向剖面图。研究表明，真假目标成像效果差异主要表现在距离和方位向目标峰值有所偏移，以及方位像聚焦效果比真实目标要稍微差一些。为了量化其成像效果，表2给出了真实目标、文献［9］方法以及本文所提方法生成目标的成像品质指标。量化指标主要包括目标距离向和方位向峰值位置偏移误差、目标方位向冲击响应宽度（IRW）、目标方位向峰值旁瓣比（PSLR）以及目标方位向积分旁瓣比（ISLR）。表2中每项指标的第1行、第2行和第3行分别为真实目标、文献［9］方法和本文所提方法生成虚假目标的成像指标数值。从图8和表2，以及对比图7可知，对于离干扰机距离较远的目标，相比与所提方法，文献［9］方法中虚假目标方位向和距离向峰值位置偏移量随着生成的虚假目标离干扰机距离增大而增大，且成像品质略微下降，其主要体现在文献［9］方法中目标方位向PSLR和ISLR比所提方法的略微增大。主要原因是文献［9］方法没有考虑式（7）中的后3项，它涉及到补偿虚假目标所在位置与干扰机所在位置的调频斜率差，以及补偿目标像峰值位置偏移量。

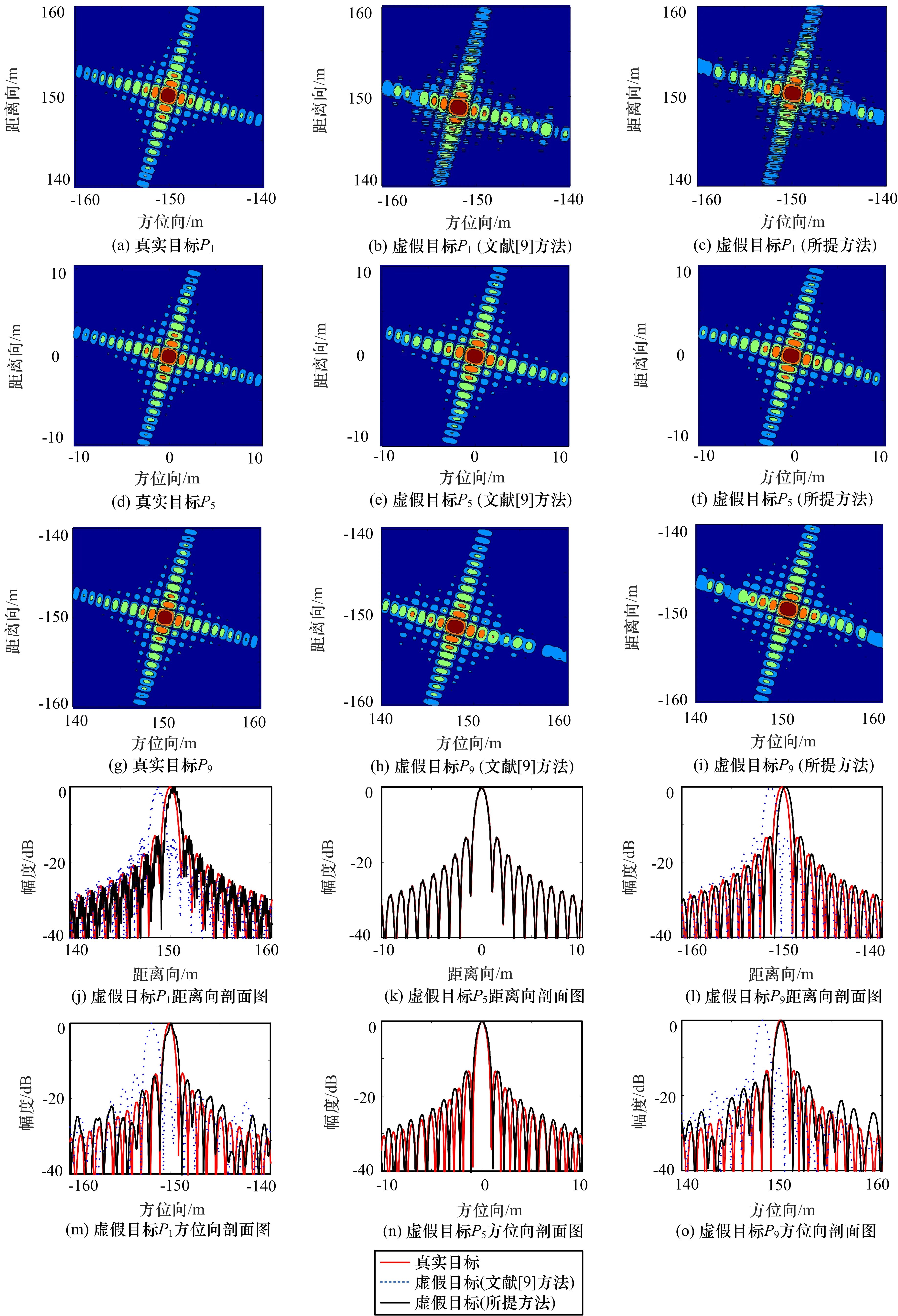
图8 真假目标升采样成像对比图（相邻目标间距150 m）

表2 不同SAR欺骗干扰方法的目标成像品质指标对比

图7 真实和虚假目标升采样剖面图对比

最后，验证文献［9］方法和本文所提方法的干扰实时性。文献［9］方法和本文所提方法均是基于多接收机协同来获取SAR的一些关键参数，其时间开销相当，实时性的差异主要源于对干扰信号的调制算法上。文献［9］方法是采用式（2）进行干扰信号调制，而本文所提方法是采用式（14）进行干扰信号调制的。由式（2）可知，文献［9］方法在截获到SAR信号后，距离向延时处理直接利用卷积进行计算，且在每个脉冲重复间隔（PRI）期间均需进行1次卷积运算。若截获的SAR信息在距离向上的采样点为Nr，且共有n个虚假点目标需要生成，则卷积的计算复杂度为O(nN2r)［12］，其中符号O表示“正比于”；而对于所提方法，距离向延时处理采用FFT代替卷积运算，在每个PRI期间，在距离向上只需1次FFT运算和1次IFFT运算，其计算复杂度为O(2nNrlog2(nNr))［12］。为了定量分析算法的实时性，在计算机上测试2种方法所需运行程序的时间。对于每种方法，假设相关的侦察参数均已计算完成，距离向采样点为1 508，共有9个虚假目标需生成，程序运行从调制截获的SAR信号开始计时，SAR信号调制完成结束计时，两者的时间差记为程序的运行时间。计算机配置为CPU主频3.2 GHz，内存16 GB，进行1 000次蒙特卡洛实验并取程序运行时间的平均值。在每个PRI期间，文献［9］方法和本文所提方法的程序运行平均时间分别为1.59×10-3s和2.65×10-5s。由理论和定量分析可知，本文所提方法的干扰实时性要优于文献［9］方法。

5 结束语

为进一步优化文献［9］方法，本文研究了一种改进的基于多接收机协同SAR欺骗干扰方法。理论分析和仿真实验表明：1）本文所提方法能够精确地对SAR载机平台进行无源测向，这为干扰机对SAR实施干扰提供干扰方位基准；2）相比于文献［9］方法，本文所提方法的欺骗干扰效果和实时性要更好一些。值得指出的是，本文所提方法需要预先知道载机高度，这对于星载SAR而言通常容易获取，而对于机载SAR而言可能需要额外的侦察设备。因此，进一步改进本文所提方法，使其无需预先知道SAR载机平台高度先验信息将是下一步需要研究的问题。