一种基于CFD-DEM的箔条散射运动数值模拟方法

王栋欢，肖洪，吴丁毅

（西北工业大学动力与能源学院，陕西 西安 710129）

0 引言

在雷达无源对抗中，箔条无源干扰是自二战以来使用最为广泛的无源干扰技术之一［1］，它通过大量喷撒铝质或者表面涂覆金属的条状纤维构成的空中干扰物，能够在一定的空间范围内产生干扰回波，以掩护己方目标不被攻击［2］。

目前针对箔条无源干扰技术的研究主要分为两个方面，一方面是箔条云团运动扩散的研究，另一方面则是关于箔条云团雷达散射截面（RCS）以及回波多普勒特性的研究［3］。散射箔条云团的运动是一种特殊的气固两相流动。众多学者致力于发展数值方法来研究气固两相流动，这些方法大体可以分为以下3种：欧拉-欧拉法、欧拉-拉格朗日法、拉格朗日-拉格朗日法［4-7］。欧拉-欧拉法提出将离散粒子群视为一种伪流体的假设，由此得到了描述准粒子流体及其相互作用的3个准粒子流体守恒方程［8-10］。欧拉-拉格朗日法采用离散元方法（DEM）或离散相等模型（DPM）处理离散颗粒的运动，其大致方法是将牛顿运动方程应用于单个颗粒或特定颗粒群，通过对单个或多个颗粒建立不同的阻力模型，实现气固两相耦合［11-14］。拉格朗日-拉格朗日法在处理粒子运动问题上与欧拉-拉格朗日法基本类似，不同的是对气体运动的描述采用基于纳维-斯托克斯方程或格子-玻尔兹曼模拟进行求解［15-17］。与欧拉-欧拉方法相比，后两种方法对颗粒运动的描述是基于单个或多个真实粒子的，因而具有更高的精度和真实性。然而，受限于计算能力和计算资源，拉格朗日-拉格朗日法在工业生产及工程应用中使用较少，相比较而言，基于欧拉-拉格朗日方法的CFD-DEM耦合模型在气固两相流数值研究中显示出越来越多的优越性。

在欧拉-拉格朗日方法中，基于CFD-DEM的耦合模型被广泛应用［18-20］，DEM在处理单个颗粒物运动上优势大，然而在针对类似于箔条等不规则条状或大颗粒物占据多个CFD网格的气固耦合中仍旧面临巨大挑战，如图1所示。本文基于CFD常用软件Fluent的用户自定义函数（UDF），结合DEM，建立了适用于气体-条状物混合流动的CFD-DEM耦合模型，探究了CFD-DEM耦合算法的详细计算流程，同时应用该模型对箔条散射结构进行了预测，给出了箔条散射运动过程的合理化解释。

图1 条状/固体颗粒物占据多个CFD网格示意图

1 数学模型

1.1 气体流动控制方程

应用CFD-DEM研究气体-颗粒的混合流动，气体流动遵循质量守恒和动量守恒，其矢量形式的守恒方程为：

式中，气体粘性应力张量tg为：

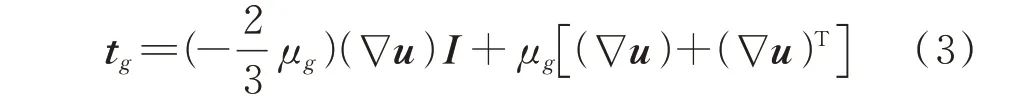
式中，α为空隙率，即气相体积分数；μg表示剪切粘性的动力粘性系数；Sp是动量交换源项，代表颗粒相施加于流体相单位体积的阻力，该阻力与颗粒所受曳力为相互作用力；∇为哈密顿算符，其展开式为：

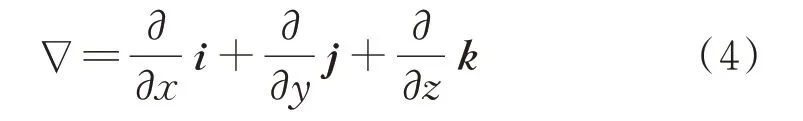
Sp体现了两相耦合关系，其影响因素众多，可由下式计算得出：

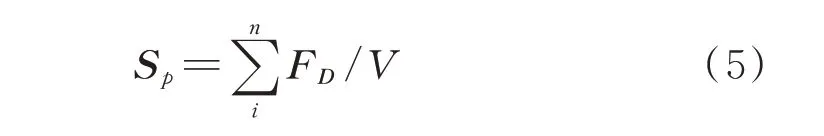
由式（5）可知，动量交换源项Sp等于作用在网格单元内流体阻力FD的总和。式中V为CFD网格单元体积。由牛顿第三定律可知FD为流体对颗粒曳力的反作用力，在CFD-DEM耦合中，典型的曳力模型为3类，将在后文具体给出。

气相体积分数α可用式α=1-αs简单求得，其中αs是颗粒的体积分数，通过抽取样本点的方法计算颗粒的体积分数简单有效。首先对每个颗粒单元抽取均匀分布的样本点Nsample，然后对每个样本点进行检验，确定出颗粒i位于某一CFD网格单元中的样本点数Si，因此可得到颗粒在某一CFD网格单元中的体积分数为：

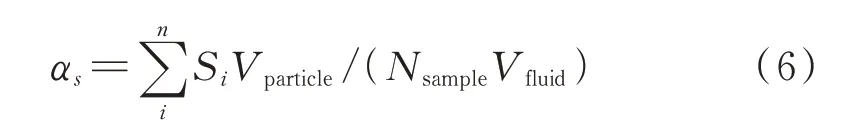
式中，n表示某一CFD网格单元中颗粒的数目。显然，样本点个数Nsample越大，αs的值越精确。对于颗粒体积小于网格体积60%的情况，可以直接利用公式求解(Nsample=1)即能达到满足要求的求解精度。

1.2 湍流模型

考虑到湍流的影响，基于雷诺平均法（RANS）对气体流动控制方程进行时均化处理，并采用Reynolds应力方程模型（RSM）。为了简化计算，忽略浮力、系统旋转及固体壁面反射的影响。由于RSM模型适用于充分发展的湍流，对于近壁面的流动，Re很低，RSM模型不再适用，因此，采用避面函数法求解近壁区域的流体速度。

1.3 不规则大颗粒物运动的数学模型

在DEM中，应用牛顿第二定律对颗粒的运动进行描述。质量为mi、体积为Vpi的颗粒i平移及旋转运动的控制方程可表示为：

运用运动学方程更新每个颗粒位置即：

式 中，Fcn，ij和Fct，ij分 别 表 示 颗 粒i与 颗 粒j的 法 向 碰 撞力和切向碰撞力；Ii、wi、Ri和nij分别表示颗粒i的转动惯量、角速度矢量、颗粒球心到碰撞平面的距离以及颗粒i与颗粒j之间的法向单位矢量。

这里，(∑Fi)表示颗粒i受到的合力，包含曳力、重力、浮力、压力梯度力、附加质量力、Basset力、Saffman升 力、Magnus升 力、热 泳 力 等。在 本 文 的CFD-DEM数值模型中只考虑重力和曳力。此外本文采用简单的线性模型即Hertz-Mindlin非滑动接触模型描述不规则大颗粒物之间的相互作用。其相互作用力通过滑块、减振器和弹簧进行模拟［21-23］。

考虑到不规则大颗粒物占据多个CFD网格的情况，在自由流阻力模型的基础上引入当地网格投影面积Alocal，因此，作用在单个颗粒上的曳力描述如下：

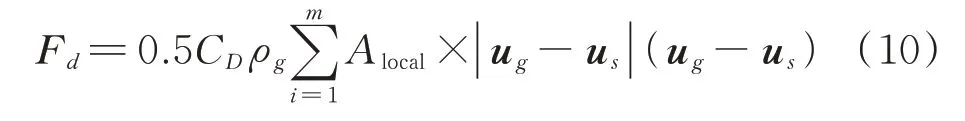
式中，m为颗粒占据的网格数；ug为气体速度；us为颗粒运动速度；CD为单颗粒曳力系数，其大小与颗粒雷诺 数Rep有 关［24-25］；Alocal是 颗粒在当地网格 下的投 影面积，如图2所示。

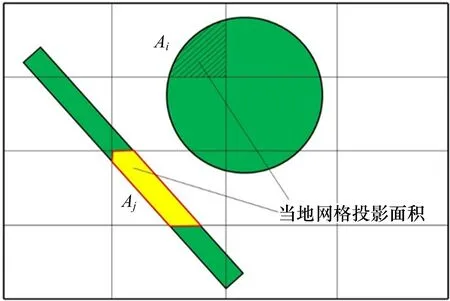
图2 条状/不规则大颗粒物占据多个CFD网格投影面积示意图

对颗粒接触力的求解采用DEM，利用牛顿第二定律进行各个颗粒的运动求解时采用了整体坐标系，然而颗粒接触力的计算是在局部坐标系下完成的，因此在颗粒接触力计算部分需要进行坐标变换。将整体坐标中的相对位移转换为局部坐标中的相对位移，之后才能直接应用相关接触模型进行接触力的计算，并且在求解得到接触力的值后，还需进行第二次坐标转换，将法向、切向方向上的接触力分量投影变换到整体坐标系当中，进行力的求和计算［26］。颗粒接触力的计算大体可分为：

第一步：载入模型的特征参数；

第二步：读取接触配对单元在整体坐标系下的坐标值，计算相对位移并进行坐标转换；

第三步：利用接触模型中的接触力-位移关系计算弹性力和阻尼力；

第四步：计算切向力和颗粒单元的接触力在绝对坐标系上的投影分量，以及旋转力矩；

第五步：判断接触对象是颗粒还是边界，计算接触对象的受力。

1.4 CFD-DEM耦合模型

气体与颗粒之间的耦合可分为3种：单相耦合、双向耦合和四相耦合。单相耦合只考虑气体对颗粒的作用力；双向耦合同时考虑气体对颗粒、颗粒对气体的相互作用力；四相耦合则是在双相耦合的基础上还考虑了颗粒与颗粒间的相互作用。对于颗粒体积分数小于10%的稀相流，考虑气体-颗粒的双相耦合，应用Fluent自带的DPM模型可以得到较满意的结果；而对于颗粒体积分数较大的气体-颗粒混合流动，需考虑气体-颗粒间的四相耦合。CFD-DEM耦合模型的最大优点是同时考虑了气固间的动量交换、颗粒体积分数对流场的影响以及颗粒间的相互作用，其适用性更广，求解精度更高。

在CFD-DEM耦合计算过程中，耦合模块基于Fluent的UDF函数及DEM模块的输出接口，实现了Fluent与DEM模块之间的数据交换。该耦合计算过程中，Fluent首先在一个时间步长内求解气相流动，同时调用CFD-DEM耦合模块计算颗粒的曳力并传递给DEM模块，接着DEM模块计算每个颗粒的运动并通过耦合接口将空隙率及动量源项传递给Fluent，最后Fluent加载源项及空隙率并进行下一时间步内的迭代求解，其耦合计算流程如图3所示。一般情况下，在求解流场的一个时间步内，DEM模块迭代计算10到100次。CFD计算时间步长（TF）与DEM模块时间步长（TDEM）的大小关系为：

图3 CFD-DEM耦合计算流程

2 数值模拟

采用发展的CFD-DEM耦合方法，对箔条散射过程中的箔条云运动进行了数值模拟。选择拉瓦尔喷管附加直径280 mm、长度390 mm的圆柱腔作为箔条散射的研究模型。拉瓦尔喷管长110 mm，入口直径28 mm，出口直径50 mm，喉部直径20 mm。几何结构如图4所示。采用Block块网格划分方法，整个计算域被划分为结构化的六面体网格，图5为计算模型结构及网格。

图5 计算模型结构化网格图

选取箔条数量为1 000个，初始任意堆积于喷管近出口内部，如图4所示。箔条形状简化为圆柱体结构，密度为500 kg/m3，直径为0.2 mm，长度为15 mm。具体参数及计算的边界条件为：拉法尔喷管进口直径为28 mm，长度L为110 mm，出口直径为50 mm，网格数量为745 324个，喉部直径为20 mm，箔条直径为0.2 mm，长度为15 mm，数量为1 000个；边界条件进气总压为2 000 Pa，Ma数为0.1。

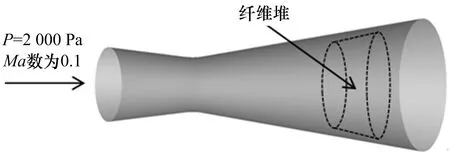
图4 喷管结构图

图6 给出了不同时刻下箔条的散射状态，由图可得初始静止状态的箔条在气体曳力的作用下瞬间从喷管喷出，在百分之一秒的时间尺度上即可呈现出散状分布。初始静止的一堆箔条经0.02 s后平均速度达到8 m/s，箔条云形状似一半球。随着时间的推进，中心区域箔条被吹向最前端并逐渐散开，箔条云中心区域速度最大，边缘处箔条速度较小。在0.02 s时刻，箔条云变为锥形，最大速度出现在锥顶处，速度大约为13 m/s。0.04 s时刻下锥状箔条云被拉长，最前端箔条的速度可达到16 m/s。在气流的作用下，中心箔条的运动处于一个加速的过程，当中心箔条被完全吹开后速度逐渐降低，受圆柱形空腔长度的限制，当前构型尺寸下未能显现出箔条云完全被吹开时箔条的最大位移。

图6 不同时刻箔条散射结构图

3 结束语

本文提出了一种适用于求解箔条散射运动的CFD-DEM耦合方法，利用该方法对1 000数量箔条散射结构进行了仿真模拟。研究结果表明，箔条散射结构初始为半球体，进而发展为椎体，箔条云中心区域速度最大，边缘处箔条速度较小。模拟结果初步表明本文提出的CFD-DEM耦合方法可以模拟箔条散射运动，且能得到符合预期的箔条散射结构。

本文对于箔条散射的数值模拟只停留在数值仿真层面，并未涉及与之对应的实验验证。此外，现有的箔条散射数值模拟算例工况较为单一，只给出了单一速度工况下箔条云团随时间的初步散射结构特性。因此，今后还需通过实验和具体工程问题，进行多种工况的仿真计算。