磨粒有序化砂轮磨削微沟槽减阻表面的研究＊

王俊博， 吕玉山， 慕 丽， 李兴山

（沈阳理工大学 机械工程系, 沈阳 110159）

1983年，WALSH[1]通过研究不同类型微沟槽表面的减阻效果，证明了有一定微结构的工件表面能够降低摩擦阻力，为微观结构化表面的减阻技术奠定了基础。随着学者们的深入研究，微沟槽结构表面也被证实在转子-轴承系统、机械密封、活塞环-缸套系统润滑、切削刀具等领域可以极大地改善工件表面的摩擦性能[2]。

为了获得工件的微沟槽表面，研究者提出了磨削、激光加工、滚压、电化学腐蚀等制造方法。而磨削法在解决超硬材料的批量化生产方面具有独特的优势，很多国内外学者对此开展了利用砂轮磨削结构化沟槽表面的研究。STEPIEN等[3-5]首次在砂轮表面修整出螺旋沟槽，在工件上磨削出了沟槽结构。DENKENA等[6-7]利用金刚石修整辊修整砂轮，磨削出仿鲨鱼皮沟槽表面。KIM等[8]使用金刚石修整器在砂轮表面修整出螺纹槽，在工件上磨削出了沟槽结构。MOHAMED等[9]使用带有圆周方向凹槽的砂轮在工件上磨削出了沟槽表面，通过研究磨削参数对沟槽表面形貌的影响，建立了磨削运动模型，并预测了工件的表面形貌。GUO等[10]利用超声振动在工件上磨削出了V型沟槽。XIE等[11-12]使用碳化硅油石修整金刚石砂轮，磨削出了沟槽尖角圆弧半径为22～24 μm的沟槽。

目前，制造结构化砂轮的方法主要分为2类：一类是通过磨粒的有序化排布来实现有序化表面砂轮的制造；另一类是对砂轮表面进行修整。但在沟槽表面的磨削加工中，砂轮的修整技术仍是难点，因其修整难度较大，很难保证修整精度以及修整后的耐用度等。而磨粒有序化砂轮自1997年开始便被多个国家的学者用来磨削加工一些难加工材料。AURICH等[13]制造出磨粒有序化砂轮，将仿真与磨削试验相结合，得出磨粒有序化砂轮能显著提高磨削性能；SILVA等[14]利用有序化砂轮在工件表面磨削出了阵列排布的凹坑；陶思远等[15]利用有序化砂轮在工件表面成功磨削出凸台、凹坑、沟槽等结构。

但由磨粒合理的排布方式及排布参数制造出的砂轮，磨削出满足减阻参数要求的工件微结构表面仍需进一步研究。因此，采用磨粒叶序、错位、阵列3种排布方式制造出磨粒有序化砂轮，在工件上磨削出微沟槽减阻表面，讨论3种磨粒排布方式砂轮磨削的可行性。

1 磨粒有序化砂轮的设计

图1是磨粒在砂轮上的3种有序化排布方式，分别为叶序排布、错位排布和阵列排布。其中叶序排布的砂轮在圆周方向上只排布单颗磨粒，且相邻2颗磨粒的轴向间距远小于磨粒直径。设rs为砂轮半径，rm为磨粒的公称半径。 当磨粒的排布方式为叶序排布时，各磨粒中心的坐标方程如式（1）：

图1 3种磨粒排布示意图Fig.1 Schematic diagram of three abrasive arrangements

其中：θ 为叶序角度，取 θ=137.508°；H为相邻两行磨粒的轴向间距，mm；n为磨粒的序数，n=1, 2, 3, 4, ···。

当磨粒的排布方式为错位排布时，各磨粒中心的坐标方程为：

其中：j为磨粒的列数。

当fix（n/j）为 奇 数 时 ， ϕ =2×（n-1）×π/j； 当fix（n/j）为偶数时， ϕ =2×（n-1）×π/j+φ，φ为磨粒错位角度。

当磨粒的排布方式为阵列排布时，各磨粒中心的坐标方程为：

2 满足减阻的磨粒排布条件

图2是磨粒有序化结构砂轮磨削沟槽表面的示意图。其中：vs为砂轮线速度，m/s；vw为工件进给速度，mm/min。在磨削过程中，磨粒的轴向排布间距决定了沟槽的间距，磨粒的平均磨削深度决定了沟槽的平均深度。因此，要优先确定沟槽表面减阻特性参数，以此来设计有序化砂轮。

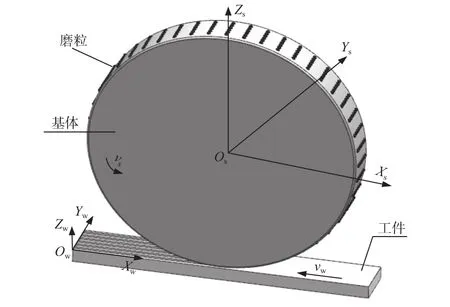
图2 磨削示意图Fig.2 Schematic diagram of grinding

影响沟槽减阻效果的主要参数为沟槽间距s和沟槽深度hg，其参数比hg/s在 0.200～1.000最佳[16-18]。因此，为了得到减阻效果较好的沟槽结构，需要对沟槽的参数进行设计。磨粒的形状虽然多种多样，各不相同，但参与磨削部分的磨粒尖端的轮廓形状可以近似看为三角形。当磨粒按照阵列顺序排布时，生成沟槽的示意图如图3所示。

图3 阵列排布Fig.3 Array arrangement

各个磨粒露出的高度用hgn表示，露出高度最大值为hgmax。在磨削前需进行对刀，露出高度最大的磨粒接触到工件表面时便完成了对刀。但是由于每个磨粒露出的高度具有随机性，因此，除了最高磨粒产生的沟槽深度为ap，其他磨粒生成的沟槽深度不能都按磨削深度ap来计算。因此，用hn来表示第n颗磨粒生成的沟槽深度，则有：

由于磨粒露出的高度满足均值为 µ，方差为 σ2的正态分布[19]，那么阵列排布的磨粒所产生的沟槽的平均深度h可以表示为：

将式（4）代入式（5）中可得：

但由于磨粒阵列排布时，圆周方向上磨粒排布的数量较多，故将从 µ和 µ +3σ之间选出一个新的均值，即：

将式（6）代入式（7）中可得：

若想第n个沟槽满足hn/s≥/s，即满足hn≥。结合式（4）和式（8）可知hgn≥µ+2.5σ。

生成第n个沟槽的磨粒满足平均参数比h/s要求的概率为：

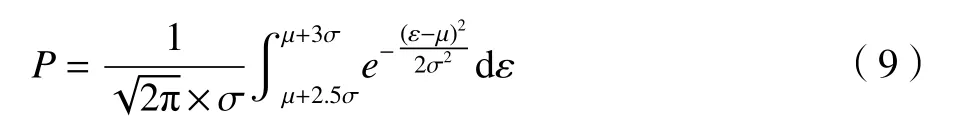
由此可见，当磨粒按阵列排布时，沟槽的减阻参数与磨粒露出高度和磨削深度有关，所产生的沟槽深度均值为，其沟槽深度与间距的比值可用来表示。由于阵列排布受磨粒尺寸的限制，其间距s无法小于两磨粒的平均直径，进而影响沟槽深度与间距的比值，使其无法达到最佳的减阻参数，而错位排布和叶序排布恰好解决了这一问题。当磨粒按照错位和叶序排布时，生成沟槽的示意图如图4所示：

图4 叶序和错位排布沟槽示意图Fig.4 Arrangements of phyllotactic and staggered

当排列方式为错位排布时，磨削深度ap难以达到沟槽干涉的临界值，磨粒所生成的沟槽没有发生干涉，沟槽的生成方式与阵列相同；当排列方式为叶序排布时，由于相邻磨粒排布间距更小，因此磨削深度ap容易达到沟槽干涉的临界值，产生的沟槽两两相互干涉如图5所示。

图5 沟槽干涉形成示意图Fig.5 Schematic diagram of groove interference formation

设点O为原点，磨粒1的高度为hg1，尖端为点C；磨粒2的高度为hg2，尖端为点B；两磨粒投影交点为点A，磨粒1和磨粒2之间的间距为s，两磨粒与砂轮基体交点分别为a，b，c，d。为了方便计算将2个磨粒的尖角度数均看作相等的 2 α，设磨粒1的露出宽度bd为l1，磨粒2的露出宽度ac为l2，ab之间的长度用lab来表示：

根据三角函数关系可得：

根据三角形相似有 (l2-lab)/l2=h′/hg2，那么可得：

此时左、右侧沟槽深度可表示为：

若想第n个沟槽满足即满足结合公式可推出hgn＞hgn-1，则第n个沟槽的参数比大于平均参数比的概率为P=0.5。

由此可见，当忽略磨粒尖角的度数差异后，叶序排布的磨粒所生成的沟槽参数主要与磨粒的间距和磨粒的尖角度数有关，且当磨削深度ap≥h′时，沟槽均值为h。

3 沟槽表面形貌仿真

3.1 仿真方法和条件

结合磨粒坐标方程和磨粒运动轨迹方程，利用MATLAB软件分别对磨粒叶序、错位、阵列3种排布的砂轮磨削出的沟槽表面形貌进行仿真建模，其中仿真方案参考文献 [20]。仿真中砂轮基体直径D=100 mm，磨粒直径范围为0.30～0.35 mm，公称直径dg=0.33 mm。磨粒平均露出高度参考文献[14]，取=0.46dg=0.15 mm。由于所有磨粒露出高度并不相等，因此为了使更多的磨粒能够参与磨削，减少空沟现象的发生，需要赋予磨削深度ap一个初始值为约为0.009 0 mm。磨削深度为0.05 + 1.96σ，即0.067 6 mm；通过之前的计算可知，若想达到良好的减阻参数比，需满足ap≥h′。因此，磨粒叶序排布时选择排布间距s=0.04 mm；磨粒错位排布时选择间距s=0.40 mm；磨粒阵列排布时，由于受到结构的影响选择间距s=0.80 mm；砂轮转速ns= 3 000 r/min，进给速度vw=60 mm/min。使磨粒尖端角为60°来进行仿真[16]，此时减阻性能最好。

3.2 仿真结果与分析

当磨粒的排列方式为叶序排布时，其沟槽形貌仿真图如图6a所示。此时沟槽的间距s=0.04 mm，平均波峰高度约为-50.119 0 μm，平均波谷高度约为-50.151 8 μm，沟槽的平均深度=0.032 8 mm，参数比为=0.820。将仿真参数代入式（15）中，磨粒尖端角度取60°，得到理论平均沟槽深度为0.034 6 mm，理论参数比为0.866。仿真结果与理论计算的预期值基本吻合。

当磨粒的排列方式为错位排布时，其沟槽形貌仿真图如图6b所示。此时沟槽的间距s=0.40 mm，平均波峰高度约为-50.107 5 μm，平均波谷高度约为-50.171 7 μm，沟槽的平均深度=0.064 2 mm，参数比为0.160。将仿真参数代入式（8）中，得到理论平均沟槽高度为0.063 1 mm，理论参数比为0.157。仿真结果与理论计算的预期值基本吻合。

当磨粒的排列方式为阵列排布时，其沟槽形貌仿真图如图6c所示。此时沟槽的间距s=0.80 mm，平均波峰高度约为-50.106 9 μm，平均波谷高度约为-50.171 2 μm，沟槽的平均深度=0.064 3 mm，参数比为=0.080。将仿真参数带入式（8）中，得到理论平均沟槽深度为0.063 1 mm，理论参数比为0.079。仿真结果与理论计算的预期值基本吻合。

图6 沟槽表面仿真图Fig.6 Simulation of groove surface

通过仿真结果可以看出：当砂轮上的磨粒为叶序排布时，此时相当于单颗磨粒完成沟槽的磨削，由于磨粒露出的高度具有随机性，因此所形成的沟槽深度也各不相等，沟槽的参数比在0.200～1.000较为理想；当砂轮上的磨粒为错位排布时，相当于多颗磨粒完成一个沟槽的磨削，因此所形成的沟槽较为稳定，沟槽的参数比接近0.200，但不如磨粒叶序排布时产生的参数比理想。当砂轮上的磨粒为阵列排布时，与磨粒错位排布时相同，也相当于多颗磨粒完成一个沟槽的磨削，因此所形成的沟槽也比较稳定，然而沟槽的参数比较小，并不理想。

4 磨削试验

由电镀试验制备出的3种排布的有序化砂轮如图7所示。由于H决定了沟槽结构的排布间距s，因此为了得到理想的参数比，将在排布结构允许的情况下，将相邻两行的磨粒尽可能地紧密排列。由于受到磨粒尺寸大小的限制，磨粒之间的间距过小会对后续的电镀试验造成影响。经过多次试验并结合前期仿真工作的验证，最终使叶序砂轮取H=0.04 mm，错位砂轮取H=0.40 mm，阵列砂轮取H=0.80 mm，并在五轴加工中心进行磨削试验。

图7 有序化砂轮Fig.7 Ordered grinding wheel

被磨工件采用45#钢，硬度为36～42 HRC，表面粗糙度为 0.3 μm。砂轮转速ns=3 000 r/min，磨削深度ap=0.050 0 mm，工件进给速度vw=60 mm/min，磨削后得到如图8所示的3种沟槽表面，并在轮廓仪上测量出沟槽表面的截面轮廓图，如图9所示。

图8 磨削出的沟槽表面Fig.8 Groove surface by grinding

由图8可知：磨粒阵列排布和错位排布的砂轮磨削出的工件表面没有缺沟现象，而叶序排布的工件表面出现缺沟现象。这是由于当磨粒阵列和错位排布的砂轮磨削工件表面时，相当于多个磨粒参与磨削，个别磨粒的磨损对整体形貌的影响不大；而当磨粒叶序排布的砂轮磨削工件表面时，相当于单颗磨粒独自完成磨削，又由于磨削过程中磨粒的磨损和电镀时的工艺误差，出现缺沟现象。

由图9中可知：磨削出的3种工件表面的沟槽间距s与预期设计结果基本吻合，分别约为0.04 mm、0.40 mm和0.80 mm。由于电镀时的工艺误差，使得沟槽间距s在数值上略有偏差。3种工件表面的沟槽平均深度分别约为0.013 0 mm、0.038 0 mm和0.033 0mm。对比理论计算、仿真结果与试验结果可知，工件表面的沟槽深度与理论计算结果相差不大。由于砂轮制造精度问题，砂轮上的磨粒在同一周向排布有一定偏移并导致某些相邻沟槽发生干涉，且在电镀试验时无法保证空镀所产生的底镍层一样高，两者差别导致各个磨粒在砂轮表面的出刃高度各不相同，引起了磨粒等高性的误差，从而使沟槽平均深度与预期设计有一定误差。由于磨粒的各个尖角的度数具有随机性，在砂轮表面的姿态也各不相同，参与磨削的磨粒尖端的角度与仿真设计的角度也存在一定偏差，因而导致实际磨削出的叶序表面的沟槽深度与仿真时的深度存在偏差，试验得到的参数比与仿真结果和理论计算的参数比存在偏差。结合得到的试验数据可计算出磨粒叶序、错位、阵列3种排布磨削出的沟槽表面的参数比分别为0.325、0.095和0.041。

图9 沟槽表面截面轮廓图Fig.9 Groove surface section profile

5 结论

（1）利用磨粒有序化排布砂轮磨削工件能够制备出微观减阻的沟槽表面，实现这一磨削方法的前提条件是合理地选择砂轮的磨粒排布参数和磨削用量。其中磨粒叶序排布时，相邻两行的轴向间距H为0.04 mm；磨粒错位排布时，H为0.40 mm；磨粒阵列排布时，H为0.80 mm。磨削深度为0.050 0mm。

（2）磨粒错位排布和阵列排布的砂轮磨削出的沟槽表面更加稳定，没有缺沟现象；而磨粒叶序排布的砂轮磨削出的沟槽表面稳定性略差，出现缺沟现象。