MPCVD多晶金刚石片的研磨均匀性分析*
徐钰淳, 朱建辉, 王宁昌, 师超钰, 赵延军, 邵俊永, 徐 帅
(1.超硬材料磨具国家重点实验室, 郑州 450001)
(2.郑州磨料磨具磨削研究所有限公司, 郑州 450001)
金刚石材料具有极高的硬度、良好的化学稳定性、高热传导率、高弹性模量、大电阻、宽带隙、较宽的透光波段(从红外到紫外)及低摩擦系数等优越的物理化学、光学和热学性质,被视为21世纪最有应用前景的功能材料。现阶段大尺寸多晶金刚石晶片多采用化学气相沉积(CVD)法获得,主要包括热丝法(HFCVD)、微波等离子体法(MPCVD)以及直流热阴极法(DCPCVD)等。受CVD法金刚石晶体生长机理的制约,多晶金刚石生长过程中随着晶片厚度增加,其表面粗糙度和晶粒大小也会增大到几个甚至几十个微米[1]。并且由于内应力的影响,金刚石晶体脱离衬底后会存在一定程度的翘曲[2],必须对其进行进一步加工使其表面粗糙度及面形精度满足工程应用要求。
游离磨料研磨是一种能够实现高面形精度和低表面粗糙度的加工方法,广泛应用于大口径平面光学元件的超精密研磨中。在CVD金刚石材料去除机理方面,COUTO等[3]提出了微观解理理论,指出在CVD单晶金刚石易磨方向金刚石原子的去除方式主要是纳米级沟槽形式的塑形变形,而在其难磨方向的去除方式则是纳米级的脆性断裂。文星凯等[4]采用机械研磨方法研究了不同磨盘转速和不同压力对研磨速率的影响,并指出机械研磨CVD金刚石的材料去除机理为微切削和应力诱导的金刚石膜局部石墨化。LIU等[5]采用分子动力学模拟方法对单晶金刚石的机械磨抛过程进行了模拟,验证了在磨粒机械力作用下相比于金刚石<110>晶向,碳原子在其<100>晶向更容易产生由SP3杂化向SP2杂化转化的非晶化现象。结合游离磨料加工特点,金刚石研磨是三体加二体磨削的材料去除过程,即利用磨料对金刚石表面的微切削与划擦作用进行材料去除的。整个过程中形状各异的磨粒在抛光压力作用下,一部分嵌入抛光盘中对工件进行刻划,达到微切削的作用;一部分持续以滚动的方式对工件进行滚轧。在刻划与滚轧的相互作用下,金刚石表面的微裂纹不断扩大直至崩裂实现而去除[6]。
综合来说,在CVD多晶金刚石片游离磨料研磨领域,国内外学者的研究主要集中于金刚石材料去除机理以及研磨工艺参数、游离磨料尺寸等对金刚石表面粗糙度及其材料去除率的影响规律方面[7-10],对于大尺寸CVD多晶金刚石片在研磨加工过程中如何保证其较高的面形精度却鲜有报道。而金刚石片研磨阶段的面形精度对后道抛光工序中的材料去除余量大小以及最终面形精度起着决定性作用。因此,针对影响金刚石面形精度的主要因素-磨粒轨迹均匀性,建立旋摆式驱动平面研磨过程中的单磨粒运动学模型,并引入离散系数作为轨迹均匀性量化评价标准,探究研磨过程中工件与磨盘转速比、摆动弧的弦长等对随机多磨粒轨迹均匀性的影响,最后通过多晶金刚石片实际研磨试验,探究轨迹均匀性对金刚石片面形精度的影响规律。
1 旋摆式平面研磨单颗磨粒运动学模型
1.1 单颗磨粒几何运动状态
图1为旋摆式驱动平面研磨几何模型,主要由研磨盘、驱动电机以及连杆轴承等部件构成。根据图1提取研磨盘与工件运动关系如图2所示。假定P为研磨盘上一随机磨粒,研磨过程中认为磨粒P位置固定,则P跟随研磨盘以ω1的转速绕着圆心O1匀速转动,研磨盘半径为R;如图2所示的半径为Rd的 MPCVD多晶金刚石片贴合在夹具工装上,随着工件轴绕O2以ω2的转速转动,O1与O2之间的距离为e;此外,工件轴还设置有绕摆动中心O3的圆弧形往复摆动,L为摆臂长度,A为摆动弧弦长,工件轴摆动周期为T。以O1,O2为原点,建立两个局部坐标系X1O1Y1,X2O2Y2,此时P在X1O1Y1坐标系下的位置可用极坐标(r,θ)表示。

图1 旋摆式驱动平面研磨几何模型Fig.1 Geometric model of rotary swing drive plane lapping

图2 研磨盘与工件运动关系Fig.2 Kinematic relation between lapping plate and workpiece
当不考虑工件轴往复摆动时,此时的研磨方式相当于偏心距为e的定偏心式研磨,磨粒P相对于工件的运动是P绕O1的转动叠加工件轴绕O2的转动。根据坐标变换原理,将P点在坐标系X1O1Y1下的坐标(r,θ)通过平移旋转后在坐标系X2O2Y2中的坐标表示为(x',y'),则在不考虑工件轴往复摆动时,P相对于工件的运动方程为:

上式中当研磨盘与工件同向旋转即转速比为正时,ω2前取“-”号,反之取“+”号。
由图2可知:工件轴往复摆动弧的中点与坐标系X2O2Y2的坐标原点O2重合,则摆动圆心O3在坐标系X2O2Y2下的坐标可以表示为(Lsin(arcsin(e/L)),Lcos(arcsin(e/L)))。设工件轴摆动弧对应的摆动角度为2λ,得到λ=arcsin(A/2L)sin(2πt/T),其中根据图1所示的连杆轴承结构可知工件摆动周期T与工件轴转动周期一致,则有T=1/ω2。综合可得工件绕O3摆动的轨迹在坐标系X2O2Y2中的运动方程为:

综合式(1)~式(2)得到磨粒P相对于工件的运动轨迹方程为:

式中:xi,yi为点P在X2O2Y2坐标上的轨迹坐标。在金刚石片平面研磨过程中,研磨液中的磨粒随着供液装置滴落在研磨盘上。假设参与研磨过程的磨粒在研磨盘上的分布是均匀随机的,磨粒在金刚石片上各位置的去除量一致并且在短时间内研磨盘上的磨粒分布状态近似。为模拟研磨过程中真实的磨粒分布状态,计算机仿真时采用随机分布算法将多颗磨粒分散在整个研磨盘上,如图3所示,研磨盘中间的空白区域为装夹预留孔,此部分磨粒不参与研磨过程。
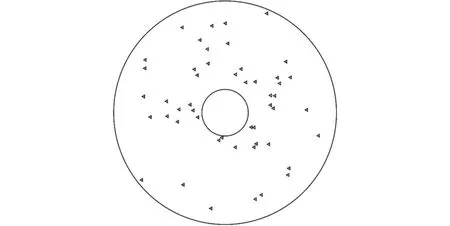
图3 研磨盘随机磨粒分布示意图Fig.3 Random abrasive distribution on the lapping plate
1.2 随机分布的多磨粒轨迹均匀性评价方法
根据旋摆式磨粒轨迹运动方程,对不同参数下随机分布的多磨粒运动轨迹均匀性进行评价。首先根据磨粒轨迹方程模拟出研磨一定时间后虚拟工件上多磨粒如图4所示,后对轨迹图像进行灰度处理,利用二维微单元[11-13]方式对虚拟工件进行网格划分,使用像素点统计的方法计算每个微单元格内磨粒轨迹像素点数量信息并生成总样本Q,引入离散系数CV作为随机多磨粒轨迹均匀性的评价指标,离散系数大小不仅受变量值离散程度的影响,而且还受变量值平均水平大小的影响,具体表达式为[14]:

图4 工件网格划分示意图Fig.4 Schematic diagram of workpiece meshing

式中:CV为离散系数,xi为第i个微单元内磨粒轨迹像素点数,μ为统计样本Q的算术数平均值,n为网格单元个数。离散系数越小,轨迹均匀性越好,反之均匀性越差。
2 转速比对轨迹均匀性的影响
研磨时工件盘转速ω2与研磨盘转速ω1的选取对研磨均匀性具有显著影响。设转速比I为工件盘转速与研磨盘转速二者绝对值的比值,即

其中:“ + ”代表二者转速方向相同,“-”则表示二者相反。
此外,在研磨过程中,若磨粒的磨削时间超过一定时间Tr后,磨粒运动轨迹就不再变化,只重复原来轨迹,定义Tr为轨迹稳定周期。根据式(2)可知工件摆动周期T与工件轴转动周期T2相同,此时研磨盘的转动周期T1与工件盘转动周期T2满足以下关系[15]:

式中:k,m,n为自然数,k为ω1、ω2的最大公约数。则根据式(6),可以得到轨迹稳定周期:

根据式(7),为获得磨粒完整周期轨迹选择的仿真时间时应大于稳定周期。具体仿真参数如表1所示。

表1 计算机仿真参数Tab.1 Parameters of computer simulation
取研磨盘转速ω1为63 r/min,转速比取0~1.0,间隔0.1变化,根据式(7)计算得到此时轨迹稳定周期Tr最大值约为9.52 s小于表1中选取的仿真时间,因此得到的磨粒轨迹均为完整周期。由于采用随机算法设计磨粒分布状态,为避免一次随机导致磨粒轨迹离散系数计算结果不具代表性,造成计算误差,因此在计算同一组参数下磨粒轨迹离散系数时,取5次计算结果平均值作为最终结果。虚拟工件表面磨粒轨迹仿真部分结果如图5a~图5d所示,其分别表示转速比取1.0,0.5,0.4,0.1时的磨粒相对于工件的轨迹曲线。由图5可知:虚拟工件表面磨粒轨迹均为泛摆线。当转速比为1.0时,磨粒轨迹曲率最小,轨迹接近于直线;随着转速比降低磨粒轨迹线曲率变大。当转速比为0.5时(如图5b),磨粒轨迹存在大量留白现象,具体表现为局部轨迹间隔较大或过于集中,整个工件表面磨粒轨迹分布较为离散。图5c~图5d中相比于前两者,转速比为0.4和0.1时,轨迹更均匀。通过计算得到研磨盘转速为63 r/min时不同转速比对离散系数影响的变化规律,如图6所示,可以发现当转速比取值在0.5两侧时,轨迹离散系数变化规律具有相反的规律。转速比小于0.5时,二者为正相关,即离散系数随转速比降低而逐步降低;当转速比增大至大于0.5时,轨迹离散系数出现先减小后增大的趋势。根据计算结果,在选择转速比参数时,上下盘转速应避免在0.5附近取值。当转速比取0.1时,其磨粒轨迹离散系数较低,在实际研磨过程中材料去除均匀,理论上可以得到较好的研磨面形精度。

图5 不同转速比下虚拟工件磨粒轨迹Fig.5 Virtual workpiece abrasive trajectory under different speed ratio

图6 转速比对轨迹离散系数的影响规律Fig.6 Influence of rotational speed ratio on trajectory dispersion coefficient
3 摆动弧弦长对轨迹均匀性的影响
旋摆驱动式平面研磨工艺参数中除转速比外,另一个影响轨迹均匀性的重要因素是摆动范围大小,衡量单个周期内摆动范围大小的指标为摆动弧弦长A,计算机仿真时设置磨粒数n1为50,研磨盘转速ω1为63 r/min,转速比为0.1,摆动弧弦长从0~110 mm间隔10 mm依次变化,共计12组参数,其余参数与表1保持一致。通过仿真得到随机多磨粒轨迹,如图7所示。当摆动弧弦长A为0时,此时相当于定偏心式研磨,磨粒轨迹如图7a所示,可以看出定偏心式研磨仿真得到的磨粒轨迹具有明显规律性,磨粒轨迹的离散系数相对较大,工件表面局部位置处出现轨迹集中现象;当A为30 mm时,磨粒轨迹如图7b所示,此时磨粒轨迹均匀性有所改善但轨迹分布仍不均匀;当A进一步增大至50 mm以上,如图7c~图7d所示,磨粒轨迹分布均匀性明显提升。各组离散系数变化规律如图8所示。图8中:随着摆动弧弦长A逐渐增大,磨粒轨迹离散系数出现2个阶段,第一阶段当A为0时,轨迹离散系数最大,且随弦长增大而急剧下降,随后暂时稳定;第二阶段当弦长A大于50时,轨迹离散系数从稳定进一步减小而后到达稳定状态。可见相较于弦长A小于虚拟工件直径r时的情况,当弦长A>r时,磨粒轨迹均匀性有较大改善,不再出现磨粒轨迹集中于工件某一局部的现象。因此,在实际的研磨加工过程中,为了达到较好的面形精度,采用旋摆式驱动平面研磨时,工件摆动弧弦长选择要大于工件的直径。

图7 不同摆动弧弦长下的磨粒轨迹Fig.7 Abrasive trajectory under different chord length of oscillating arc
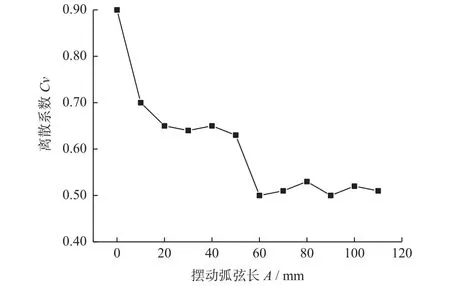
图8 摆动弧弦长对离散系数变化规律的影响Fig.8 Influence of the chord length of oscillating arc on the variation of dispersion coefficient
4 研磨加工试验与结果
4.1 试验平台及检测设备
MPCVD多晶金刚石片实际平面研磨试验在单面研磨机(JINGPING-01)上进行,如图9所示。研磨盘材料为铸铁盘(HT200),外径为500 mm,内径为120 mm,开槽形式为1 mm宽的十字槽。工件夹具是直径为75 mm的不锈钢盘。

图9 旋摆式驱动研磨设备Fig.9 Rotary swing drive lapping equipment
通过调节转速器功率可以改变研磨盘以及工件载盘转速大小,如图10所示,旋摆式运动方式是通过电机驱动偏心轮连杆轴承转动来实现工件载盘的旋转以及往复摆动,通过调整连杆轴承的偏心距可以调节平面研磨时实际的摆动弧弦长大小。

图10 研磨机摆动驱动模块Fig.10 Swing drive module of lapping machine
研磨结束后,将工件放入无水乙醇中通过超声清洗机清洗20 min,除去表面研磨液残渣及杂质,然后使用白光干涉仪(GT-X,德国Bruker)测量工件表面的粗糙度,使用光学轮廓仪(VR-5000,日本Keyence)测量工件的面形精度,通过电子分析天平(AUW320,日本岛津)测量研磨前后材料去除量大小。
4.2 研磨最优转速比工艺试验
由于受生长工艺的影响,通过MPCVD异质外延方式生长的多晶金刚石不同样品间的本征应力存在差异;且在沉积过程中金刚石沿厚度方向晶体晶粒大小是变化的,具体为靠近生长面的晶粒较粗,靠近形核面的晶粒则较小。但多晶金刚石材料的断裂韧性与晶粒大小存在一定关系,而其断裂韧性进一步影响着研磨最终表面质量以及材料去除率等[16-17]。因此,为统一试验参数,避免加工对象差异对结果产生影响,研磨试验中采用材料属性较为均一的蓝宝石假片进行最优研磨工艺探索,蓝宝石片假片直径为2 inch(1 inch=2.54 cm),研磨液磨料为单晶金刚石,粒度代号为325/400。在设备稳定运行的前提下,设置研磨盘转速为60 r/min,通过调节工件盘转速使得转速比在0.10~0.50范围内间隔0.05取值;为保证材料去除的均匀性,固定研磨机摆动驱动模块中偏心轮连杆轴承的偏心距为70 mm,使实际研磨时满足摆动弧弦长大于工件直径的要求。每组蓝宝石样品研磨时间为40 min,研磨结束后测量其研磨表面的平面度PV值。假片实际研磨的平面度与离散系数计算结果如图11所示。由图11可知:随着转速比不断变化,假片研磨最终面形精度PV值与磨粒轨迹离散系数变化趋势较为一致,可得研磨最优转速比为I=0.1时,工件PV值以及离散系数CV均最小。

图11 试验值与仿真计算结果对比Fig.11 Simulation results are compared with the experimental values
4.3 实际研磨试验
实际研磨时,根据最优工艺参数,设置研磨盘转速为63 r/min,工件盘转速为6.3 r/min,摆动中心偏心距e=120 mm,摆动周期为9.52 s,加载压力为40 N,研磨液磨料为单晶金刚石,粒度代号为325/400,研磨液流量为2 L/min,研磨工件是由郑州磨料磨具磨削研究所有限公司提供的2 inchMPCVD光学级金刚石毛坯片,初始厚度为0.8 mm,研磨面为金刚石长晶面,初始粗糙度为10 μm,PV值为90 μm。金刚石片粘接方式为石蜡粘接,研磨时间为180 min。
研磨结束后对金刚石片的表面粗糙度以及面形精度进行测量。其中,粗糙度取样点位置如图12所示,整个面共取 13 个点,取样点面积为 137 μm × 164 μm,测量结果如图13所示。由图13可见:金刚石表面不同位置粗糙度基本一致,粗糙度Ra最小为139 nm,最大为149 nm,平均值为144.46 nm,标准差s为3.15 nm。金刚石片长晶面研磨后的面形精度如图14所示,此时工件表面PV值为2.4 μm。

图12 金刚石片研磨表面粗糙度采样位置Fig.12 Sampling position of diamond abrasive surface roughness

图13 金刚石片研磨表面粗糙度结果Fig.13 Results of lapping surface roughness of diamond wafer

图14 金刚石片研磨表面面形精度PV值Fig.14 PV value of surface precision of diamond lapping surface
通过表面粗糙度结果可以认为此时金刚石工件的原始表面已全部去除,为了衡量金刚石研磨的材料去除率dMRR,首先通过电子分析天平测量此时工件的原始质量,将工件再次装夹继续研磨120 min,每隔30 min将工件取下称重,共进行4组试验,通过计算得到各组金刚石研磨的材料去除率dMRR如图15所示,可知最优参数下金刚石研磨dMRR平均值为10.1 μm/h。
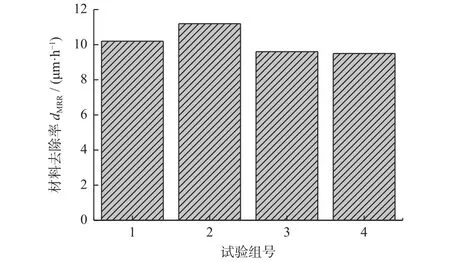
图15 金刚石研磨材料去除率Fig.15 Diamond abrasive material removal rate
5 结论
通过建立磨粒轨迹运动模型,并引入轨迹离散系数评价指标,探究了旋摆驱动式研磨运动参数对2 inch多晶金刚石晶片材料去除均匀性以及面形精度的影响,并通过实际研磨试验验证了方法的有效性,并得出以下结论:
(1)研磨盘与工件盘转速比对磨粒轨迹离散系数有显著影响,当转速比小于0.5时,转速比与虚拟工件的离散系数呈正相关,即在满足设备正常运行的情况下适当降低转速比有利于提高材料去除均匀性。
(2)摆动弧弦长大小对磨粒轨迹均匀性影响存在2个阶段,随着弦长不断增大,在初始阶段,研磨方式由定偏心驱动变为旋摆式驱动,轨迹离散系数急剧减小,随后暂时稳定;当弦长进一步增大至大于50 mm时,轨迹离散系数再次降低,最终达到稳定阶段。
(3)通过假片研磨试验找到最优工艺参数,然后进行2 inch多晶金刚石片实际研磨试验,研磨后金刚石表面粗糙度较为一致,粗糙度Ra最小值为 139 nm,面形精度PV值为2.4 μm,金刚石片研磨材料去除率dMRR平均值为 10.1 μm/h。

