基于互补电阻开关的忆阻乘法器设计

李志刚，陈辉，刘鹏，武继刚

（广东工业大学 计算机学院，广州 510006）

0 概述

传统的冯诺依曼体系结构分别在存储器和中央处理单元进行数据存储和计算。因此，物理上分离的存储器与中央处理单元之间需要进行频繁的数据通信，导致性能开销和能耗增加。为提高计算机性能，研究人员探索利用新型非易失性纳米器件构建“非冯诺依曼”架构的新领域［1-2］。忆阻器具有存算一体、尺寸小、低功耗等多种特性［3］，成为“非冯诺依曼”架构的关键器件［4］。近年来，基于忆阻器的数字逻辑电路设计被广泛应用于人工神经网络以及通信电路设计等领域。但关于忆阻乘法器的研究多数通过传统的部分乘积算法来实现，存在串行化进位比特问题，导致延时和面积开销增大。

为解决该问题，本文提出一种弱进位依赖的忆阻乘法器，通过对乘法运算中的进位比特进行拆解，减弱计算过程中的进位依赖，使得加法操作并行化，最终实现在线性时间内的忆阻乘法器。利用互补电阻开关（Complementary Resistive Switch，CRS）的读出操作破坏所存储逻辑状态的特性，设计一种基于忆阻器的部分乘积运算方式，为实现忆阻乘法器奠定基础。通过对传统的TC 加法器和PC 加法器进行优化，减少加法运算的延时和面积开销。提出一种基于互补电阻开关的可并行实现的乘法运算方案，并将其映射到混合CMOS/crossbar 阵列结构之中，优化忆阻乘法器的延时和面积开销。

1 相关工作

忆阻器被广泛应用在数字逻辑设计领域中。赵毅等基于互补电阻开关提出一种可重构的忆阻器逻辑设计方法，实现了与、或、非蕴含以及异或四种基本逻辑门，并设计2-1 和4-1 多路复用器电路［5］。2-1 多路复用器需要3个忆阻器通过2个步骤实现。4-1多路复用器需要6个忆阻器通过5个步骤实现。李志刚等［6］在择多-非-图的基础上，利用忆阻器设计延时优化和面积优化加法器。延时优化的一位加法器需要4 个忆阻器通过4 个步骤实现。面积优化的一位加法器需要3 个忆阻器通过5 个步骤实现。SIEMON 等［7］从不同的优化角度，利用互补电阻开关设计TC 加法器和PC 加法器。针对面积开销性能，N位TC 加法器利用N+2 个存储单元通过4N+5 个步骤实现。针对延时开销性能，N位PC 加法器利用2（N+1）个存储单元并通过2（N+1）+2 个步骤实现。

在传统的二进制乘法器中，乘法运算可分为部分乘积计算、部分乘积位移以及部分乘积累加共3 个步骤［8］。HAJ-ALI 等根据不同的 功能将忆阻交叉阵列中的一行存储单元划分为多个区域，并利用TALATI 等［9］提出的加法器实现乘法运算［8］。该乘法器可以在一行或一列中进行并行运算。而乘法运算的方式仍然采用部分乘积算法，导致单次乘法运算的延时增长。IMANI 等［10］提出一种快速加法器和近似计算存内架构，该架构利用所提的快速加法器，以降低一定的精度为前提来加快乘法器的运算速度。TAHERINEJAD 等［11］提出的半串行加法器结构。RADAKOVITS 等［12］利用文献［11］所提的半串行加法器结构进行半串行乘法的运算。对于N位乘法运算，该乘法器将2N-1 比特的半串行加法器电路构建「n/2次。在半串行加法器之间并行计算两个部分乘积，并进行「lbn次并行加法以实现乘法运算。ALAM 等设计的乘法器依赖于确定性随机计算算法。该算法将乘数和被乘数转换成特定的二进制比特流，并利用时钟分频技术对二进制比特流进行逻辑与运算来完成乘法操作［13］。该算法利用3×22n个存储单元通过3 个步骤来实现。WANG 等在择多-非-图的基础上设计一种利用3 个忆阻器通过4 个步骤实现的全加器，在此基础上，进一步利用Wallace树实现一种4 bit 乘法器。该乘法器需要51 个忆阻器并通过64 个步骤完成运算［14］。GUCKERT 等在实质蕴涵操作［15］和MAD（Memristors-as-Drivers）逻辑门［16］基础上，采用忆阻器和传统CMOS 管相结合的方式分别实现了两种忆阻乘法器［17］，并与传统的CMOS 乘法器相比，两种忆阻乘法器在延时和面积开销方面均有所优化。HAI 等［18］将数字量与模拟量相混合，设计一种用于支持矩阵乘法操作的浮点乘法器，以加快卷积神经网络的训练速度。

上述所实现的乘法操作大多是在加法器的基础上采用传统的部分乘积算法实现。而在传统的部分乘积算法中，乘法运算过程中的多个进位比特处于不同的时钟周期，并且在同一时钟周期仅利用一位进位比特。因此，现有的忆阻乘法器存在串行化加法操作，导致延时和面积开销增大。

2 忆阻器与互补电阻开关

忆阻器是具有可变电阻的双端无源器件。忆阻器的电阻值取决于两端施加的电压。忆阻器与互补电阻开关的电路结构及伏安特性曲线如图1 所示。忆阻器的器件符号和伏安特性曲线如图1（a）所示。在忆阻器两端施加正电压Vreset时，忆阻器的阻值状态会切换为高电阻状态（High Resistance State，HRS），此时对应的电阻值为Roff，表示的逻辑状态为逻辑0。在忆阻器两端施加负电压Vset时，忆阻器的阻值状态会切换为低电阻状态（Low Resistance State，LRS），对应电阻值为Ron，表示的逻辑状态为逻辑1［19］。忆阻器具有尺寸小、运算速度快、非易失性等特点，一般采用交叉阵列的形式构建。但无源忆阻交叉阵列存在漏电流问题，导致数据读取错误［9］。

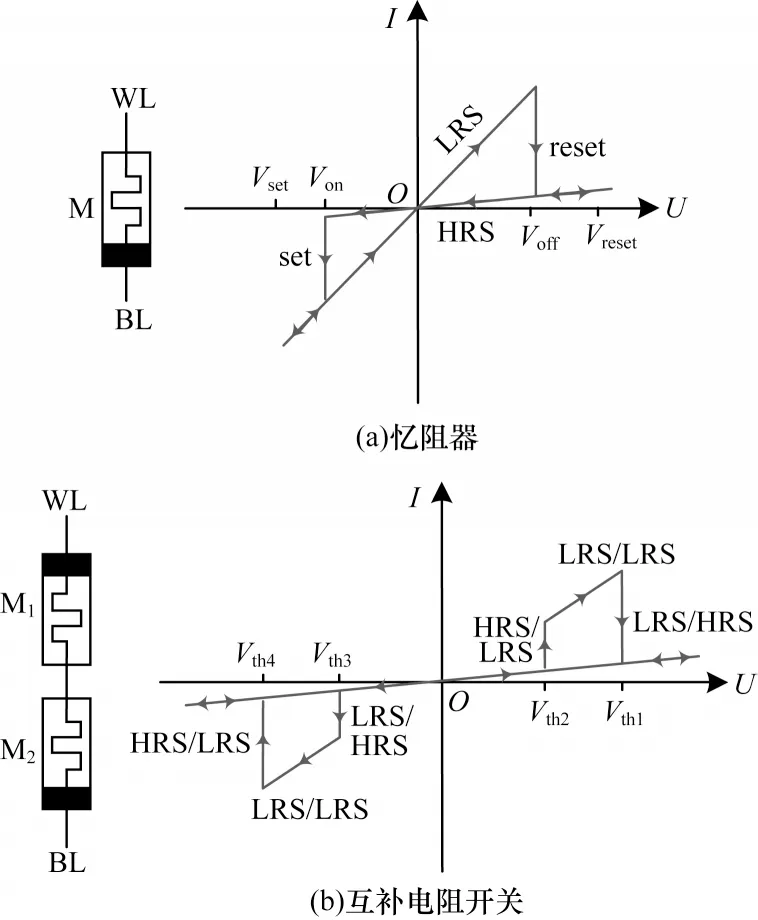
图1 忆阻器与互补电阻开关的电路结构及伏安特性曲线Fig.1 Circuit structure and volt ampere characteristic curves of memristor and complementary resistive switch

为解决无源忆阻交叉阵列中漏电流的问题，LINN 等提出CRS 结构［20］。CRS 的电路结构和伏安特性曲线如图1（b）所示。忆阻器M1和忆阻器M2的阻值状态组合表示CRS 的逻辑状态。LRS/HRS 阻值状态和施加在CRS 两端的高电压Vth1=max｛2|Vset|，2Vreset｝表示逻辑状态1，HRS/LRS 或接地表示逻辑状态0。在CRS 两端施加Vth1=max｛2|Vset|，2Vreset｝的正电压时，CRS 的阻值状态将切换为LRS/HRS。在CRS两端施加Vth4=min｛-2|Vset|，-2Vreset｝的负电压时，CRS的阻值状态将切换为HRS/LRS。在CRS 两端施加的电压在Vth2～Vth3之间时，CRS 的阻值状态不 会改变。

当CRS 处于稳定的逻辑状态时，电阻值总为高阻，施加幅值较小的忆阻器读出电压，无法区分所存储的逻辑值。因此，CRS 的读出操作是在字线（Word Line，WL）端施加大于Vth1的电压信号，同时以位线（Bit Line，BL）端接地的方式实现。从图1（b）可以看出，在CRS 两端施加大于Vth1的电压信号时，若在输出中检测到电流脉冲，则表示该CRS 的阻值状态为HRS/LRS，即逻辑0。若在电流输出中无法检测到电流脉冲，则表明CRS 的阻值状态为LRS/HRS，即逻辑1。在此读出过程中，CRS 的阻值状态会被置为逻辑1，所存储的逻辑值有可能被破坏［7］。

CRS 的逻辑转换机制由有限状态机表示。CRS有限状态机示意图如图2 所示。

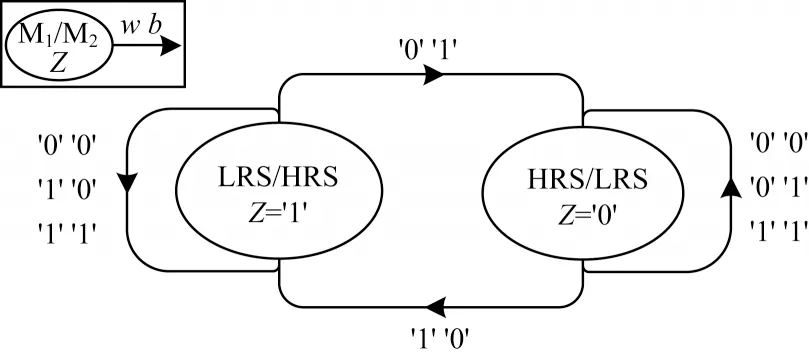
图2 互补电阻开关有限状态机示意图Fig.2 Schematic diagram of finite state machine of complementary resistive switch

CRS 的逻辑表达如式（1）所示：

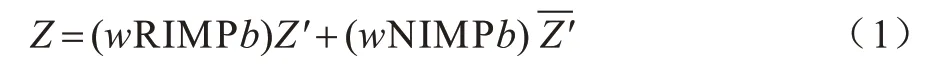
其中：w和b分别为连接CRS 字线和位线的电压信号所对应的逻辑变量；Z′和Z分别为施加电压信号前和施加电压信号后的逻辑状态；RIMP 和NIMP 分别为实质蕴含逻辑的求逆和取反。RIMP 和NIMP 的逻辑表达［21］如式（2）和式（3）所示：

LINN 等进一步利用CRS 实现了14 种基本逻辑［21］。由CRS 的逻辑表达式可知，当w为逻辑1，b为逻辑0 时，CRS 的逻辑状态将被置为逻辑1，实现了TRUE 逻辑操作：

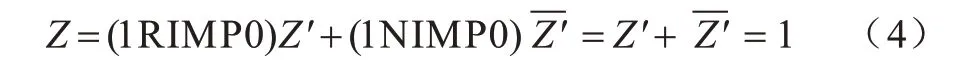
将CRS 置为逻辑状态1 后，令w为逻辑q，b为逻辑1，其逻辑状态将被置为逻辑q：

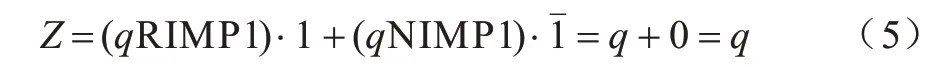
将CRS 置为逻辑状态0 后，通过将w设置为逻辑1，b设置为逻辑，也可实现置q逻辑操作：

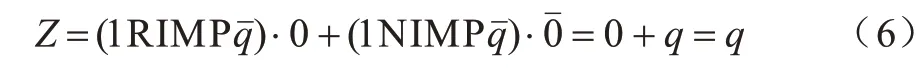
BREUER 等［22］通过简化加法器公式实现基于互补电阻开关的全加器。全加器表示如式（7）～式（9）所示：

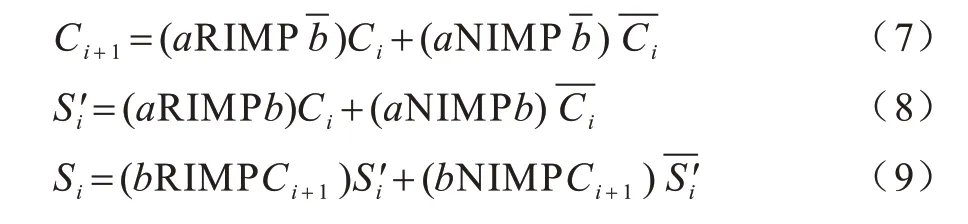
其中：a、b和Ci为一位全加器的输入；和Si分别为中间和最终求和输出值；Ci+1为进位输出值。

3 乘法器设计

本文针对延时开销和面积开销，在TC 加法器和PC 加法器优化方案基础上，利用CRS 构建乘法器电路，并将其映射到混合CMOS/crossbar 结构中。混合CMOS/crossbar 结构如图3 所示。该结构由多个阵列和一个控制单元组成。控制单元用于协调每个阵列并将信号寻址到特定的字线和位线。

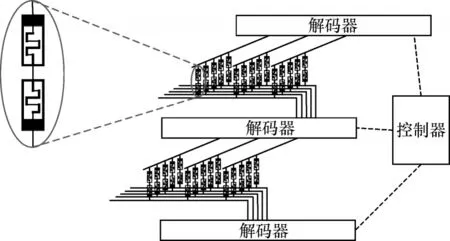
图3 混合CMOS/crossbar 结构Fig.3 Structure of hybrid CMOS/crossbar

3.1 加法器优化

加法器是乘法器运算过程中必不可少的一部分。加法器的优化有利于降低乘法器的延时开销和面积开销。在传统的TC 加法器和PC 加法器中，包括最高输出位在内的所有结果均在Ci+1和的基础上运算得到。然而，加法器的最高输出位运算结果本质上是进位比特，其运算过程并不需要计算，只计算Ci+1。因此，本文通过简化最高输出位的运算步骤来优化TC 加法器和PC 加法器。

优化后的一位TC 加法器的电路结构如图4 所示，其中A0（1）表示在阵列0 中的第1 个存储单元。优化后的一位TC 加法器的实现步骤如表1 所示。

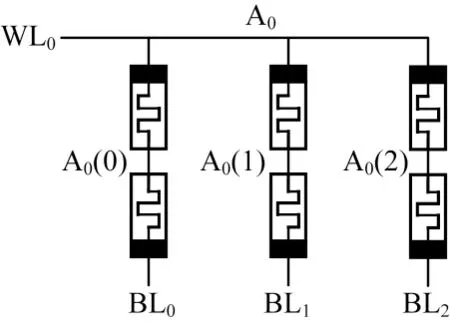
图4 优化后一位TC 加法器电路结构Fig.4 The circuit structure of optimized 1-bit TC adder

表1 优化的一位TC 加法器实现步骤Table 1 Implementation steps of optimized 1-bit TC adder

从表1 可以看出，优化后的TC 加法器的实现步骤主要有初始化操作、C0的计算、C1和的计算、读出操作以及最终S0的运算。由式（4）可知，在初始化操作中，将代表逻辑1 的高电压信号Vth1施加在WL0上，同时将BL0-2三个端口接地，A0（0）、A0（1）、A0（2）三个CRS 被置为逻辑1。为了将C0写入到A0（0）、A0（1）、A0（2）中，根据式（5）可知，表示C0和逻辑1 的电压被分别施加在WL0和BL0-2上。根据式（1）和式（8）可知，在WL0和BL1上分别施加与逻辑a和逻辑b对应的电压值，运算结果将以阻值的形式存储在A0（1）中。同时，根据式（1）和式（7）可知，在WL0上施加与逻辑a对应的电压信号基础上，BL0和BL2上施加与逻辑对应的电压值，得到两个逻辑运算结果C1，并分别存储于A0（0）和A0（2）中。其中存储于A0（0）中的C1作为最终运算结果保存，而存储于A0（2）中的C1则作为步骤5的输入。为了利用A0（2）中的C1，读出操作将读出C1的阻值。在S0的运算过程中，根据式（9），在WL0和BL1上分别施加与逻辑b和逻辑C1对应的电压信号，得到逻辑运算结果S0并存储于A0（1）中。至此，优化后的一位TC 加法器完成加法操作，C1和S0的逻辑值存储 在A0（0）和A0（1）中。

优化后的一位PC 加法器的电路结构和实现步骤分别如图5 和表2 所示。PC 加法器的前三个步骤与TC 加法器相似，唯一不同之处在于PC 加法器采用两个阵列，需要在两个WL 端施加对应的电压值。PC 加法器最关键之处在于其步骤4 利用两个阵列的并行性来同时完成C1的读出操作和S0的运算，减少了一个执行步骤。

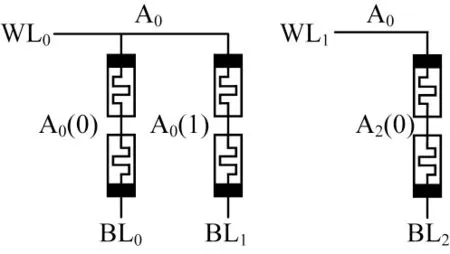
图5 优化后一位PC 加法器电路结构Fig.5 The circuit structure of optimized 1-bit PC adder

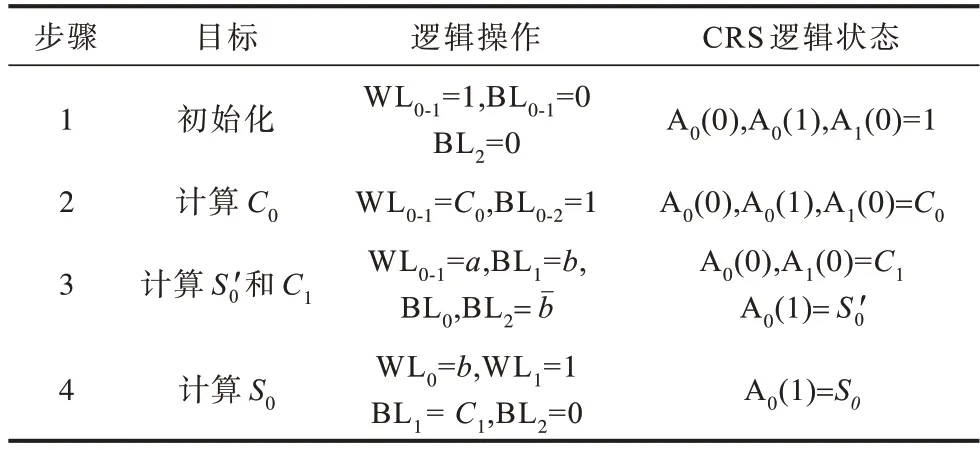
表2 优化的一位PC 加法器实现步骤Table 2 Implementation steps of optimized 1-bit PC adder

3.2 乘法器

N位乘法运算产生2N位的运算结果，其中包含了大量的加法运算。如何优化乘法运算的加法过程尤为重要。在传统的乘法计算过程中，只有完成低位的加法运算后，才能产生相应的进位比特并开始高位的加法运算过程，极大地限制了计算速度。为了提高乘法运算中加法的并行性，本文基于优化的TC 加法器和PC 加法器，提出一种弱进位依赖性乘法器。该乘法器基于混合CMOS/crossbar 结构的并行能力实现N位乘法运算。

在乘法运算中首要步骤是计算部分乘积。部分乘积由两比特的“与”逻辑运算得到。“与”逻辑是利用一个CRS 通过3 个步骤实现。部分乘积计算的实现步骤如表3 所示。

表3 部分乘积计算的实现步骤Table 3 Implementation steps of partial product calculation

首先，在WL 和BL 上分别施加与逻辑1 和逻辑0对应的电压信号，CRS 被初始化为逻辑1；其次，在WL 和BL 上分别施加与逻辑p和逻辑1 对应的电压信号，CRS 被置为逻辑p；最后，在WL 和BL 上分别施加与逻辑q和逻辑1 对应的电压信号，得到pq运算结果并存储于CRS 中。

乘法运算的后续步骤是对部分乘积进行加法运算。与传统乘法运算不同，本文采用分解一位进位比特为多位进位比特求和的方式来减弱乘法运算过程中的数据依赖性，使乘法运算中的加法运算过程得以并行化，加快乘法运算速度。图6 所示为二位乘法运算的进位比特分解过程以及对应的数据依赖图。圆圈表示一个三输入和二输出的加法器。指向加法器的箭头表示加法器所需的输入值，由加法器指出的箭头表示加法器的输出值。

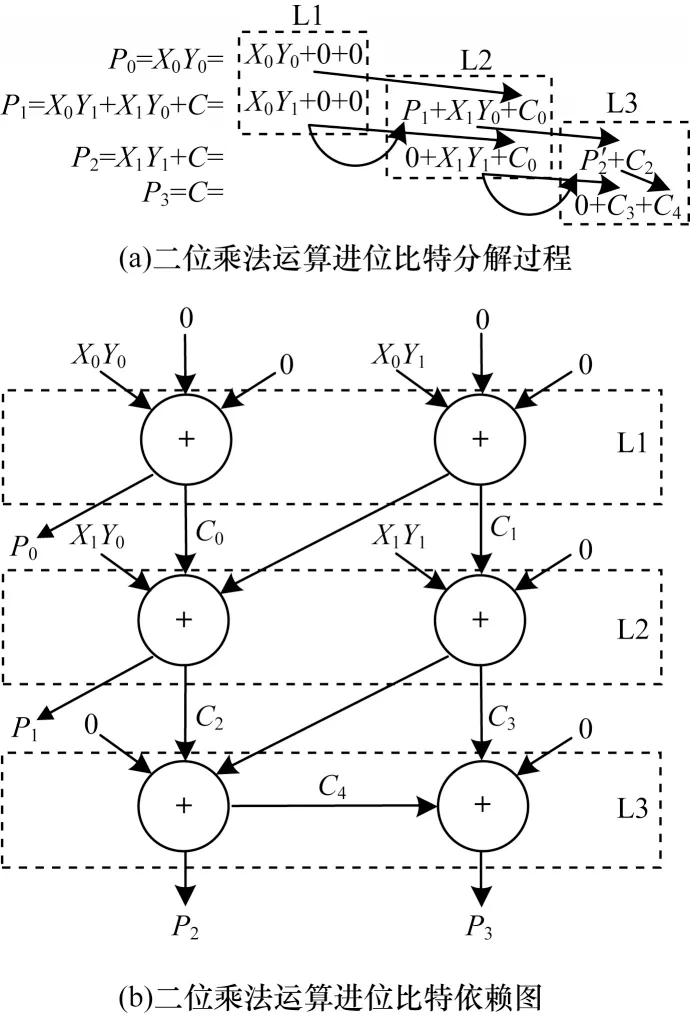
图6 二位乘法器数据依赖图Fig.6 The data dependency graph of 2-bit multiplier

从图6（b）可以看出，在完成部分乘积运算后，二位乘法器的弱化数据依赖图共有三层运算过程，包含了两层并行加法运算（L1 和L2）以及一层串行加法运算（L3）。在L3 中的两个加法器之间由于存在C4的进位依赖，因此必须串行实现。此外，每一层并行计算得到的中间计算结果用于下一层的计算。经过L1 层和L2 层的并行加法后将得到二位乘法运算结果的低2 位P0和P1。L3 层的串行加法运算将得到乘法运算结果的高2 位P2和P3。

本文采用混合CMOS/crossbar 结构实现所提的弱进位依赖性乘法器。二位乘法器的电路结构如图7 所示。

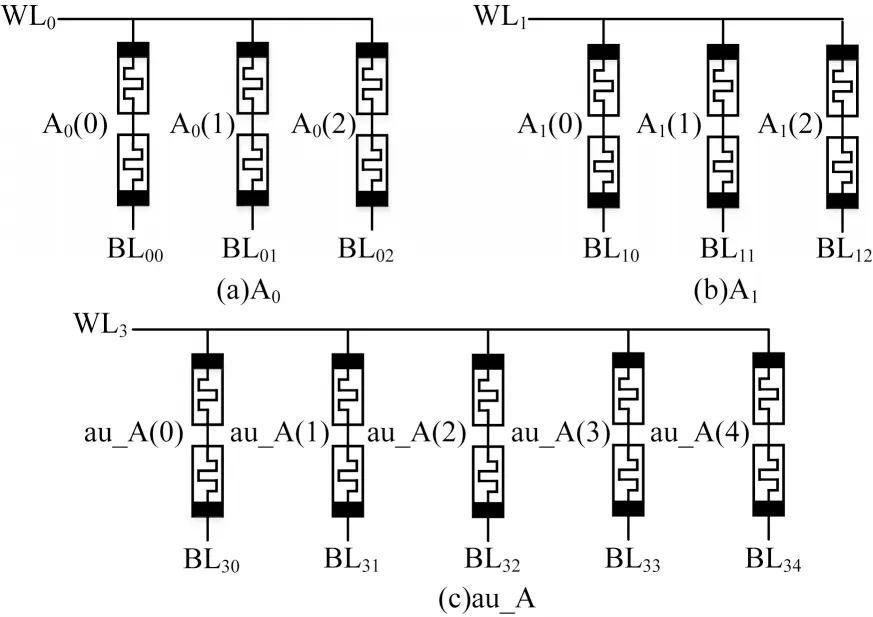
图7 二位乘法器电路结构Fig.7 The circuit structure of 2-bit multiplier

从图7 可以看出，A0（0-2）和A1（0-2）表示用于运算加法的计算阵列，au_A（0-4）表示用于存储运算结果的辅助阵列。对于二位乘法器，每个计算阵列利用3 个CRS 来执行一位加法器，辅助阵列采用5 个CRS 来存储临时和最终的运算结果。

二位乘法器的流程图和具体执行步骤分别如图8 和表4 所示。

表4 二位乘法器实现步骤Table 4 Implementation steps of 2-bit multiplier

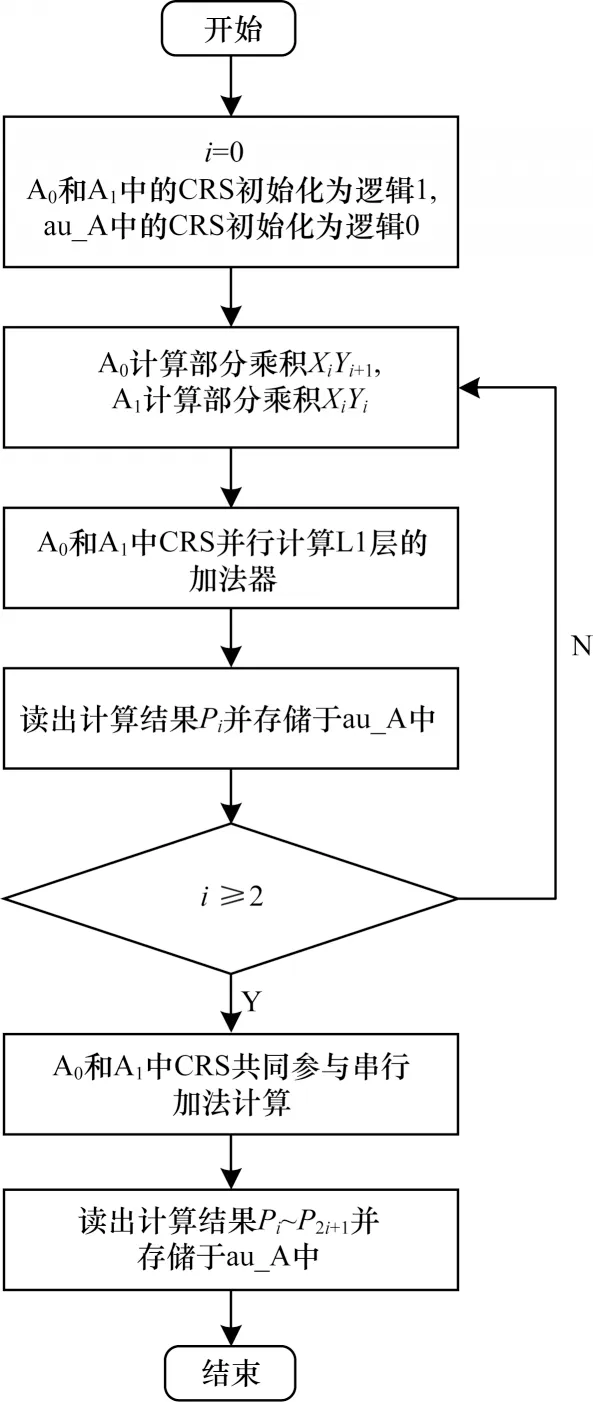
图8 二位乘法器实现流程Fig.8 Implementation procedure of 2-bit multiplier

步骤1 是初始化操作，将表示逻辑1 的电压信号施加在WL0-1上，BL00-02以及BL10-12接地，实现了A0（0-2）和A1（0-2）的置1 操作。同时，为了完成au_A（0-4）的置0 操作，外围电路将与逻辑1 对应的电压信号施加在BL20-24上，WL2接地。步骤2 和步骤3 是在BL00-02与BL10-12端口均施加代表逻辑1 的高电压，但在步骤2中WL0-1施加代表X0的电压值，而在步骤3 中，WL0和WL1上分别施加代表Y1和Y0的电压值。当步骤3 完成后，得到两个部分乘积X0Y1和X0Y0并分别存储于A0（0-2）以及A1（0-2）中。

由于本文提出的优化TC 加法器和乘法运算过程中的加法操作均可以并行实现，因此步骤4～步骤6 利用优化TC 加法器进行L1 层的并行加法。为进行L2 层的并行加法运算，步骤7 在WL0-2上施加与逻辑1 对应的电压信号，同时将BL00-01以及BL10-11接地，读出上一个步骤中的运算结果，其中包含结果P0，并进一步利用反相器在BL24上施加逻辑对应的电压信号，将P0以阻值形式重新写入au_A（4）中。

步骤8～步骤13 利用优化TC 加法器完成L2 层的并行加法运算，以得到逻辑运算结果P1并存储于au_A（3）中。为了复用存储单元，需要A0（0-2）和A1（0-2）初始化为逻辑0，因此，在步骤14 中将表示逻辑1 的电压信号施加在BL00-02以及BL10-12上，WL0-1接地。步骤15～步骤18 则利用优化的PC 加法器进行串行加法运算，最终得到逻辑运算结果P2和P3。步骤19 是在WL0-2上施加与逻辑1 对应的电压信号，同时将BL00-01以及BL10-11接地，读出P2和P3并将其以电压形式施加到BL21-22上，最终以阻值形式分别存储于au_A（1-2）中。

N位乘法运算的数据依赖图如图9 所示，其执行步骤可由二位乘法运算的步骤扩展得到。在N位乘法运算中，每层并行加法产生2N-1 位中间计算结果和一位最终乘法运算结果。为了在不同层之间重用存储单元，本文分别采用优化的TC 加法器和优化的PC 加法器进行乘法器中的并行加法运算和串行加法运算。因此，每一层的并行加法需要3N个存储单元，串行加法需要2N+1 个存储单元。

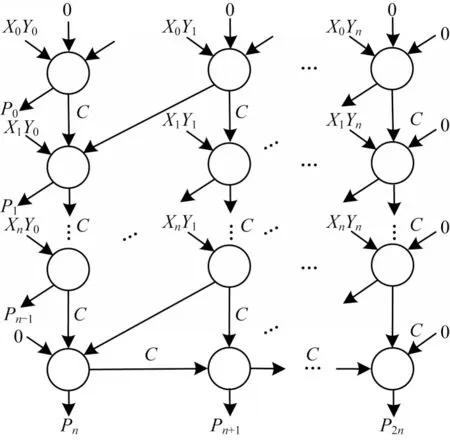
图9 N 位乘法运算的数据依赖图Fig.9 The data dependency graph of N-bit multiplier

第一层的并行操作需要7 个步骤，其中包含步骤1～步骤3 的部分乘积计算，步骤4～步骤6 的TC 加法器以及步骤7 的读写操作。由于CRS 的读出操作会将其逻辑状态重置为逻辑1，因此省略了在后续部分乘积运算中的第一步初始化步骤。N位乘法器的并行加法运算需要6N+1 个步骤。在N位乘法器中采用优化的PC加法器实现的串行加法器需要2N+2个步骤。因此，本文所提的N位弱进位依赖性乘法器需要8N+3 个步骤。此外，所需存储单元的数量将由计算阵列中的存储单元和辅助单元的总和决定。

本文所提的乘法器能够有效提升延时和面积开销性能，其原因为图6 中乘法运算方案的并行性。本文对乘法运算过程中的进位比特进行分解，减弱了进位依赖性，通过混合CMOS/crossbar 阵列结构的分阵列形式并行实现乘法运算过程中的串行加法操作，执行N个一位加法操作仅需要一位TC 加法器，极大地优化了乘法器的延时开销。此外，本文分别采用一位TC 加法器和N位PC 加法器作为乘法运算过程中的并行和串行加法器，减少额外的存储空间，在每层加法运算过程中的CRS 均可以复用，进一步减少面积开销。

4 仿真

研究人员提出多种忆阻器模型，包括Simmons隧道势垒模型［23］、非线性离子漂移模型［24］、阈值自适应忆阻器模型（TEAM）［25］、电压阈值自适应忆阻器模型（VTEAM）［26］等。VTEAM 具有简单、通用、灵活的特点。因此，本文选择VTEAM 模型进行仿真。VTEAM 模型的相关参数参考文献［26］，具体如下：Voff=0.5 V，Von=-0.5 V，Roff=2.5 kΩ，Ron=100 Ω，koff=4.03×10-8m/s，kon=-80m/s，aoff=1，aon=3，其中Voff和Von为忆阻器的阈值电压，Roff和Ron为忆阻器的高阻和低阻，koff、kon、aoff以及aon为VTEAM 模型拟合Pt-Hf-Ti忆阻器实体器件后的常量参数。在此参数下VTEAM 模型与Pt-Hf-Ti 实体器件相拟合后的伏安特性曲线可参考文献［26］。

本文利用CRS 的与逻辑实现了部分乘积。图10 所示为所有一位输入组合下部分乘积计算的仿真结果。纵坐标表示忆阻器阻值。10 ns 为一个时钟周期。从 图10 可以看出：当q=1、p=1 时，M1与M2的阻值状态分别为LRS 和HRS，代表输出逻辑1；对于其他输入情况，M1与M2的最终阻值状态分别为HRS 和LRS，代表输出逻辑0，与理论分析相符。

图10 部分乘积运算的仿真结果Fig.10 Simulation results of partial product operation

图11 所示为在a=0、b=1、Ci=1 情况下优化的TC加法器的仿真结果。从图11 可以看出，TC 加法器仿真 结果 中A0（0）和A0（1）最终的阻值状态分别为LRS/HRS 和HRS/LRS，代表运算结果为10。

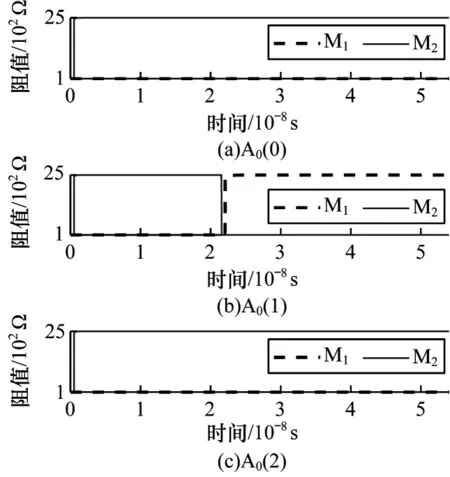
图11 一位TC 加法器的仿真结果Fig.11 Simulation results of 1-bit TC adder

图12 所示为在a=00、b=11、Ci=01 输入情况下优化的PC加法器的仿真结果。PC加法器仿真结果中A0（0）、A0（1）、A0（2）最终的阻值状态分别为LRS/HRS、HRS/LRS、HRS/LRS，表示最终运算结果为100。两种加法器的仿真结果均与理论预期相符。

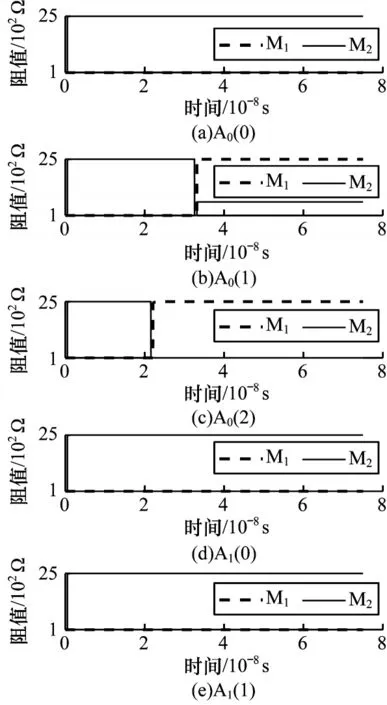
图12 二位PC 加法器的仿真结果Fig.12 Simulation results of 2-bit PC adder

本文验证输入为01 与11 情况下所提出的弱进位依赖乘法器的可行性。图13 和图14 分别所示为计算阵列A0以及A1的仿真结果。图15 所示为辅助阵列au_A 的仿真结果。从图15 可以看出，二位乘法运算共需要19 个步骤和11 个CRS。辅助阵列中au_A（1-4）的仿真结果为0011，与理论相符。

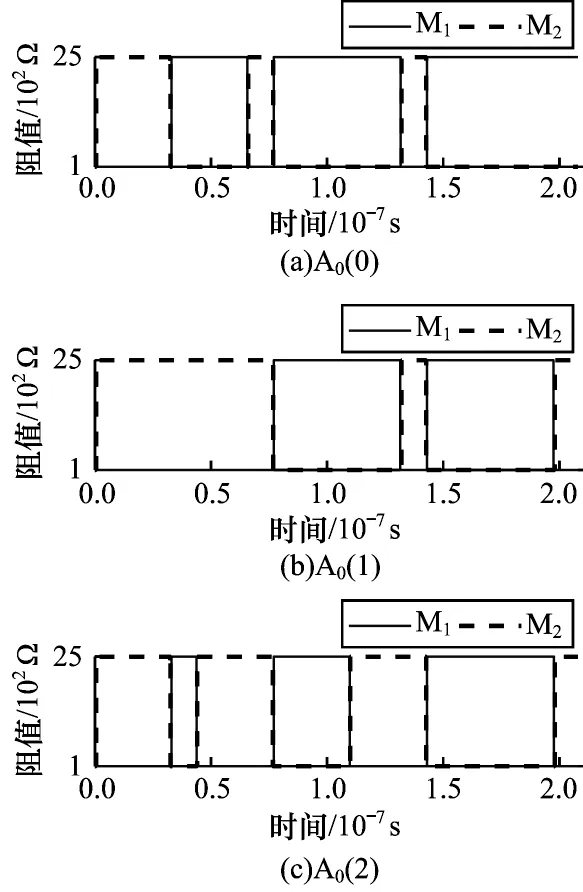
图13 在乘法器运算中A0的仿真结果Fig.13 Simulation results of A0 in multiplier operation

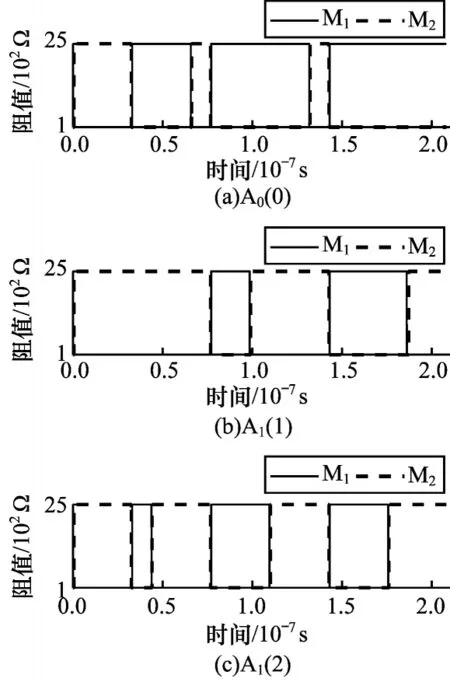
图14 在乘法器运算中A1仿真结果Fig.14 Simulation results of A1 in multiplier operation

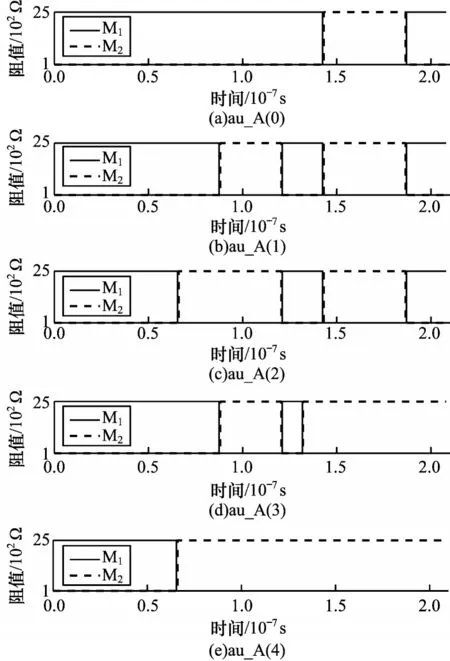
图15 在乘法器运算中au_A 仿真结果Fig.15 Simulation results of au_A in multiplier operation

表5 所示为本文所设计的方法与其他方法的结果对比，延时表示N位乘法器的执行步骤个数，面积表示N位乘法器执行所需要的忆阻器个数。与文献［8］相比，本文的延时开销降低了一个数量级，并且面积开销降低了约70%。与文献［10］和文献［12］相比，本文所提的方法在面积和延时开销性能上均降低了一个数量级。文献［13］在延时开销方面为常数级别，但其所提的方法需要在阵列的外围中增加额外的CMOS 晶体管电路，用于连接阵列的字线或位线，以构建MAGIC 电路，增加了面积开销，并且该方法并未计算输入的乘法运算数据与特定的二进制比特流之间转换所需的延时开销和面积开销。同时，本文所提的方法在面积开销方面相比文献［13］方法降低到了线性级别。

表5 N 位乘法器性能对比Table 5 Performance comparison of N-bit multiplier

5 结束语

本文针对现有忆阻乘法器设计的局限性，提出两种不同的加法器优化方案，并在此基础上设计一种乘法器。通过设计基于忆阻器的部分乘积运算，并对TC 加法器和PC 加法器进行优化，同时，针对乘法器的串行加法部分，通过减弱进位比特的数据依赖性，设计一种基于互补电阻开关的可并行实现的乘法运算方案。仿真实验结果表明，该乘法器减弱进位比特的数据依赖性，实现了并行乘法运算，与大部分现有乘法器相比，在延时和面积开销性能方面均有所提升。下一步将在本文工作的基础上，将忆阻加法器与忆阻乘法器相结合，研究忆阻浮点乘法器的实现方案，进一步完善忆阻器的复杂逻辑设计。