考虑最小尺寸精确控制的SIMP和MMC 混合拓扑优化方法1)

廉睿超 敬石开 李营 肖登宝 陈阳

*(北京理工大学先进结构技术研究院,北京 100081)

†(北京理工大学机械与车辆学院,北京 100081)

引言

拓扑优化是一种新型的设计方法,它根据给定的负载情况、约束条件和性能指标,以一定的方式寻找设计域内材料的最优分布,可生成满足特定性能需求的最优结构构型[1].与传统产品设计相比,拓扑优化可以突破设计者的思维定式,构建出更新颖、更具竞争力的创新产品.1988 年Bendsøe等[2]提出以均匀化理论为基础的拓扑优化法,经过几十年的发展和完善,此法已逐渐成为结构设计阶段的一个重要方法,被广泛应用到许多工程结构设计[3-8].当前主流的拓扑优化方法有:固体各向同性材料惩罚法(solid isotropic material with penalization,SIMP)[9-10]、渐进结构优化法(evolutionary structure optimization,ESO)[11-13]、水平集方法(level-set)[14-15]和移动变形组件法(moving morphable component,MMC)[16-17].

拓扑优化已经被拓展到了许多领域,并取得了显著成果,但其理论设计的最小结构与可制造的最小尺寸限制之间的差距,仍然是拓扑优化设计结果应用到实际工程中的重大阻碍.若结构中存在横截面积过小的部件时,即使受较小的压力也容易产生弯曲,同时设计结果中出现的孔洞或边界裂缝和细小铰链,可能会导致结构制造过程中意外断裂[18].在拓扑优化设计阶段考虑结构的最小尺寸控制可有效避免上述问题.一些学者对此开展了相关研究.

基于SIMP 的结构最小尺寸控制.SIMP 法创造性的将优化问题转变为材料的最优分布问题,极大简化了问题求解的复杂性,因其具有较高的计算效率和稳定性,已成为当前发展相对成熟且应用最广的技术.Sigmund[19]提出一种敏度过滤技术消除优化中的网格依赖和棋盘格,并发现过滤半径具有控制结构最小尺寸的能力;随后,他们在该方法的基础上,通过引入改进的Heaviside 过滤器和基于图像形态学过滤器,实现了材料相和空相的最小尺寸控制[20-21];Petersson等[22]提出拓扑优化梯度约束法,通过考虑密度梯度上的逐点边界,在保证有解的同时也可隐式的控制结构最小尺寸;Polusen[23]提出基于单调性的最小尺寸方法,应用小波基函数对材料设计变量进行插值,实现了拓扑优化中的结构最小尺寸控制;Guest等[24]提出Heaviside 投影法,以节点密度值作为设计变量,利用投影算子将密度场的节点值投影到单元空间,通过确定用于刚度插值的单元密度控制结构最小尺寸;Zhou等[25]提出几何约束的最小尺寸控制方法,结合过滤阈值拓扑优化技术,通过识别固相和空相材料实现了结构最小尺寸控制.上述研究基于SIMP 实现了结构的最小尺寸控制,但优化结果边界模糊不光滑,同时采用隐式的表达方式来描述拓扑构型,即结构不包含几何信息,难以进行精确的结构边界提取和最小尺寸控制,采用后处理工艺不仅增加了工作量和人为干预因素,而且会影响最终优化的结构性能[26-28].

基于MMC 的结构最小尺寸控制.在MMC 中,采用显式几何特征信息描述的组件作为结构的基础构件,通过它们的移动、变形和重叠实现拓扑优化.MMC 的参数化显式表达为拓扑优化结果与CAD的直接衔接提供了天然桥梁.Zhang等[18]基于MMC 框架采用不规则四边形结构组件进行拓扑优化(trapezoid-shaped structural components,TsSC),通过对组件相交区域约束实现了结构的最小尺寸控制;Wang等[29]采用基于骨架的有效连接技术(effective connection status,ECS),利用组件本身的设计变量实现了结构最小尺寸控制.基于MMC 的最小尺寸控制,在拓扑结构描述和可制造边界信息获取上具有一定优势,但其优化结果存在裂缝或不完全连接问题,且对初始组件布局具有较强的依赖性.

为了避免SIMP 优化结果边界模糊不光滑和MMC 对初始组件布局的强烈依赖,Sun等[30]通过设定SIMP 优化中的敏度阈值和组件影响区域来控制插入组件数量和位置,在SIMP 基础上实现了组件的自适应分布;范慧茹[31]和Zhang等[32-33]基于SIMP 优化结果,采用阈值处理技术得到0和1 表示的拓扑构型,利用图像处理技术识别结构骨架特征点和内切圆等几何特征,并拟合为MMC 的初始组件布局,实现了SIMP-MMC 混合结构拓扑优化,得到了尺寸精确表达的拓扑结构.采用SIMP和MMC混合的方法可以解决结构边界模糊不光滑和组件初始布局依赖问题,但上述方法中合适阈值的选择需要反复试验,尤其对包含有非常薄构型的复杂结构,易出现断裂和难以制造的最小尺寸问题,且因组件变形受限和结构的不完全连接,很难实现具有整体结构边界光滑的最小尺寸精确控制.因此,充分结合SIMP和MMC 二者优势,避免各自缺点,在不依赖初始布局的情况下获得整体结构边界清晰平滑的优化结果,并实现对结构最小尺寸的精确控制具有重要的研究意义.

基于上述原因,本文提出一种考虑最小尺寸精确控制的SIMP和MMC 混合拓扑优化方法.采用活跃轮廓算法自动识别SIMP 拓扑构型的轮廓数据,构建组件的几何参数矩阵,实现SIMP 隐式结果到MMC 显式表达组件初始布局的自动映射;通过构建具有半圆形末端的多变形组件拓扑描述函数,进一步提升优化方法构建几何模型的能力和整体结构边界的光滑性,并结合组件变量约束,实现拓扑优化结构的最小尺寸精确控制.

1 SIMP和MMC 数值模型

在SIMP 中,设计域被离散为一定数量的有限单元网格,并将密度作为设计变量赋予每个单元,利用数学规划法或基于优化准则法决定单元密度 的有无,1 表示有材料,0表示无材料,如图1(a) 所示.采用材料插值模型Ei=Emin+(E0-Emin) 解决离散优化问题,Ei为第i个单元插值后的弹性模量;E0和Emin分别为固体和空洞部分材料弹性模量; ρi为第i个单元的相对密度,ρi∈[0,1];p为惩罚因子,一般建议取3[34].

图1 SIMP和MMC 拓扑优化示意图Fig.1 Schematic of SIMP and MMC

在MMC 中,结构采用拓扑描述函数(TDF,φ(x))表达

式中,x为设计域内的点,Ω ⊂R为实体材料组件所占据的区域,R为整个设计区域.当设计区域内包含N个组件时,实体材料结构区域 Ω 内组件的拓扑描述函数可表示为φ(x)=max(φ1(x),···,φi(x),···,φN(x)),i=1,2,···,N表示组件的编号,第i个组件的拓扑描述函数可被表示为

2 SIMP和MMC 的混合拓扑优化方法

相比隐式表达的SIMP,MMC 可以通过组件的显式参数控制结构的最小尺寸,但二者结果均会出现不完全连接和细小铰链现象,如图1 所示,难以通过简单变量设置实现结构中最小尺寸的精确控制.为了解决该问题,在这一部分,将通过悬臂梁模型介绍提出的SIMP和MMC 混合拓扑优化方法实现过程.图2为悬臂梁示意图和SIMP 优化输出结果.混合拓扑优化的实现主要包括2 个部分:(1) 如何从SIMP 优化输出结果中获得组件的几何信息;(2) 如何实现SIMP 结构几何信息到MMC 组件布局的映射.

图2 悬臂梁示意图及SIMP 拓扑优化结果Fig.2 Schematic of the cantilever beam and the topology optimization result of SIMP

2.1 SIMP 优化结构的组件几何信息获取

以单元密度表示的SIMP 优化结果通常不含几何信息,难以对其进行精确尺寸控制和制造,采用图像识别技术[26]、图形插值技术[35]、密度等值线技术[36]可以获得结构的参数化模型,但这些方法通常需要较多人为干预,如密度等值线技术,在获取合适的密度阈值之前需多次反复修改模型和试验,且对复杂结构易出现断裂和非常薄的杆件问题,影响最终拓扑构型的最优性能[37].为此,在该节中,采用活跃轮廓算法(active contour without edges,ACWE)[38]对SIMP 优化输出结果的几何信息进行自动识别与提取.

ACWE 的基本思想是依据给定图形的约束,利用活跃轮廓模型通过曲线的变化识别目标对象.设在识别域 Ω 内任一变化曲线为 ξ,ω为 Ω 内边界开放的一个子集,则活跃轮廓模型可以被表示为[38]

采用水平集描述曲线变化进行求解,则活跃轮廓模型可以被重构为

通过式(8) 求解φn+1并判断其是否满足收敛,若满足收敛,则可得到目标图像的边界轮廓数据.

图3 展示了采用上述算法对SIMP 优化结果边界几何信息获取过程.为了从得到的结构边界数据中提取对应组件的边线,根据得到的每个具有相同起点和终点的闭合环,按照顺时针方向从上到下由内及外进行编号.从任意环Ci的起点(xsi,ysi) 开始,计算它与紧邻的5 个点之间形成线段的斜率k,比较点间线段的斜率差与给定阈值 δ之间的关系,若小于设定阈值 δ则判定它们在一条直线上,并从第4 个点开始依次计算随后的5 个点,直到斜率差的变化大于设定的阈值 δ,则认为在同一环中位于该条直线上的点已经结束,将第一点(xsi,ysi)和最后一点(xei,yei)作为直线的两个端点,确定一条直线.依次对后续的点进行斜率与阈值之间的比较,确定结构中所有的直线,并将其以顺时针方向按环的存储方式进行编号.基于得到的直线,从内部环的直线开始循环,计算当前环中一条直线lli与其他环中每条直线loj的斜率差Δk的绝对值和中点间距dij,将具有最小斜率差的绝对值和满足中点距离约束值dt的两条直线被视为一个组件的边界,确定结构中组件的平行边,如图4 所示.

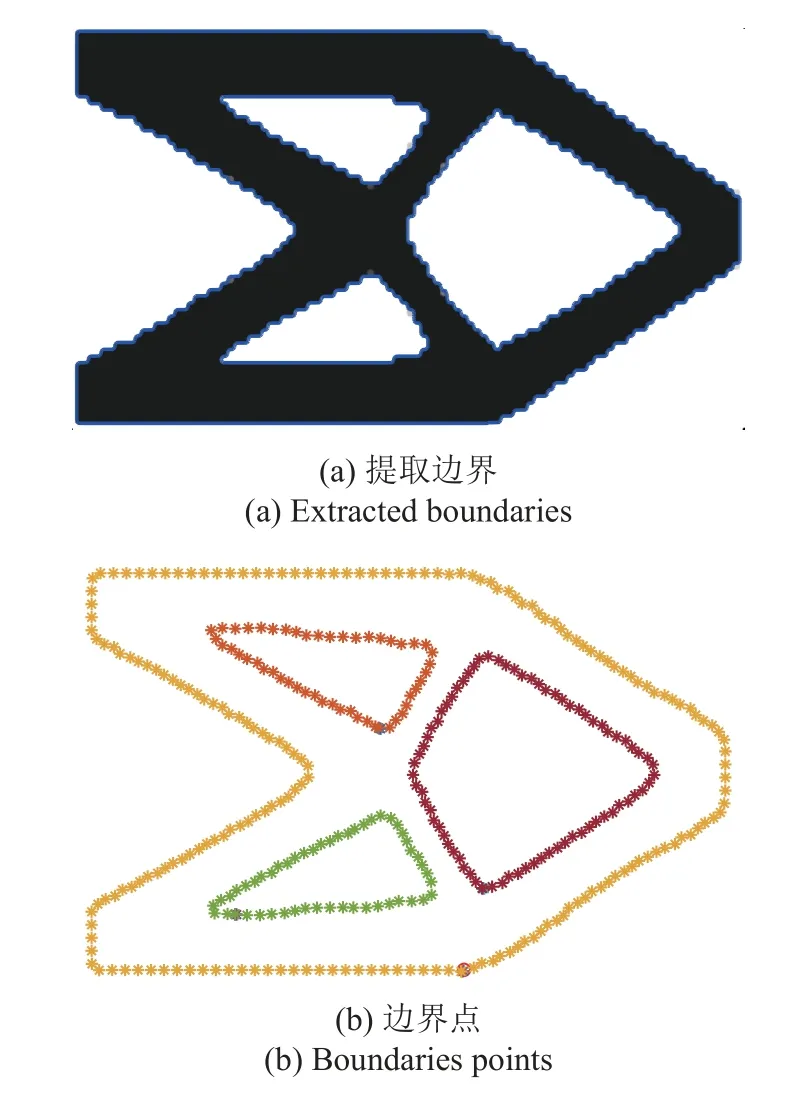
图3 ACWE 边界识别Fig.3 Boundaries identification by using the ACWE

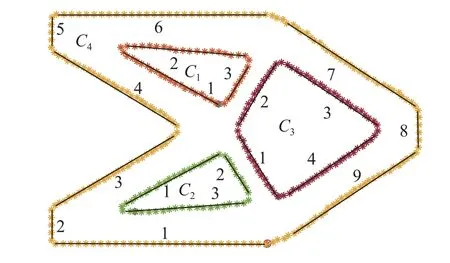
图4 边界直线及平行线识别Fig.4 Identification of straight lines and parallel lines

当每个组件的边被确定后,设χ1i和χ2i为任意组件中的两条直线,(x11i,y11i),(x12i,y12i)和(x21i,y21i),(x22i,y22i) 分别为χ1i和χ2i的两个端点,通过两点间的中点公式可以计算出两条直线两端连线的中点坐标.连接两个平行线端点连线的中点便可计算出第i个组件的中心线所在位置.然后,将中心线延长可以得到它们的交点,若出现多个交点,将它们的重心作为共同交点,通过连接各交点便可得到组件的中心线.最后,通过中点计算公式、两点间的距离公式di和斜率计算公式ki,得到每个组件的中心坐标(x0i,y0i)、1/2 长度li和1/2 厚度di、倾斜角度 θi,如图5 所示.

图5 获取组件几何信息Fig.5 Obtaining the components geometry information

2.2 组件几何信息映射为MMC 布局

在MMC 中每个组件包含长度、宽度、中心坐标、倾斜角度等几何参数,其中组件的厚度由3 个变量控制,需分别计算组件中心线两端点和中心点到对应边界的距离d1i,d2i和d3i.组件的几何信息可以通过式(10)、式(11)和式(12) 计算求得

式中,直线的斜率ki=(yi+1-yi)/(xi+1-xi).

将计算得到的组件中心坐标(x0i,y0i)、1/2 长度li,1/2 厚度di以及倾斜角度的正弦值 s inθi组装成一个参数矩阵C=[c1,c2,···,ci],ci=[x0i,y0i,li,d1i,d2i,d3i,s inθi],i=1,2,···,n,式中n为组件的总数.在SIMP 优化中获得相应的结构刚度矩阵K和参数矩阵C=[c1,c2,···,ci]时,MMC 将直接调用,形成包含SIMP 输出数据的MMC 组件自动布局.

图6为悬臂梁SIMP 优化结果映射到MMC 的组件布局.为了验证所提算法的有效性和可行性,同时采用了具有更为复杂结构的MBB 梁进行分析,得到的组件布局结果如图7 所示.由图6和图7 可知,该算法可以有效的从SIMP 隐式优化结果自动映射为MMC 中包含精确几何信息且边界清晰光滑的显式表达.但如图6(b)和图7(c) 所示,经映射后的结构边界因组件的不完全连接产生了裂缝,无法简单的利用组件厚度变量对结构的最小尺寸进行控制.如何实现混合拓扑优化中最小尺寸的精确控制将在下一小节展开讨论.

图6 悬臂梁组件映射结果Fig.6 Components mapping results for a cantilever beam

图7 MBB 梁混合拓扑优化组件映射过程Fig.7 Components mapping process of MBB beam with hybrid topology optimization

2.3 优化算法流程

本文提出的算法流程如图8 所示.在早期迭代中,采用SIMP 对设计域进行优化.在该过程中,过早的对拓扑结构进行几何信息提取,将可能会生成较多细枝结构,影响MMC 组件的初始布局.为此,在SIMP 优化过程中,当获得相对稳定的拓扑结构后,再输出结构刚度矩阵K和结构构型.利用ACWE 算法提取结构构型的几何信息,并构建组件参数矩阵C.然后,将输出的矩阵K和矩阵C作为MMC 优化迭代的初始输入参数,确定构成拓扑结构中组件数量和布局,结合设定的结构制造约束,对组件设计变量进行更新.当满足收敛条件后,优化终止,输出最终的结构拓扑构型.

图8 混合拓扑优化流程图Fig.8 Flowchart of the hybrid topology optimization

3 混合拓扑优化的最小尺寸精确控制

经SIMP 优化结果映射到MMC 组件布局后,由于组件末端采用直线表征,通过混合拓扑优化获得的构型通常会出现因组件连接不完全形成结构边界裂缝现象,无法直接利用厚度变量控制结构的最小尺寸.同时,采用直线表征组件形状,可变性受限,阻碍了其构建几何模型的灵活性,尤其是当组件数量相对较少时.为此,在SIMP和MMC 混合拓扑优化的基础上,该节提出一种形状多变的半圆末端组件拓扑描述函数,并通过构建距离约束函数和厚度变量约束函数,实现混合拓扑优化中组件的形状多变和结构最小尺寸精确控制.

3.1 半圆形末端的组件拓扑描述函数模型

设给定的任一组件i的1/2 厚度t分别通过3 个变量t1,t2和t3表示,理论上设计域内结构的最小厚度尺寸为tmin=min(2t11,2t12,2t13,···,2tn1,2tn2,2tn3),但采用直线描述组件的末端,常常会出现组件间的不完全重叠或连接现象,无法简单地通过设定组件厚度下限t来满足结构最小尺寸控制.如图9 所示,两个组件的厚度尺寸2ti1,2ti2,2ti3和2tj1,2tj2,2tj3都大于设定的最小尺寸,但其相交区域的尺寸tc却小于t,不能满足设定的结构最小尺寸约束.

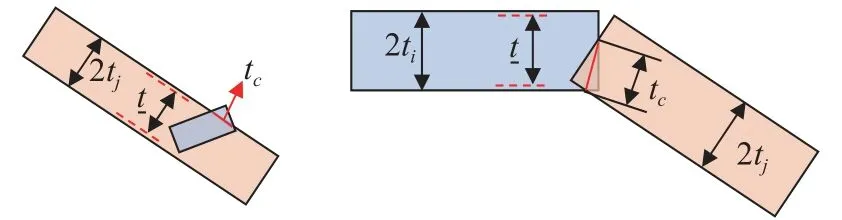
图9 组件相交示意图Fig.9 Schematic of incomplete intersection and overlap between components

为此,本文提出具有半圆形末端的组件拓扑描述函数模型,如图10所示.当相交组件其邻近末端圆心间距小于设定的阈值时,将被新的圆心坐标替代,实现组件间的完全连接.

图10 组件完全连接示意图Fig.10 Schematic of perfectly connections between components

设一个组件的形状由3 个长度变量和3 个厚度变量协同控制,如图11 所示,l1和l2分别是组件对应的两个1/2 长度;t1为组件任意一端的1/2 厚度,则需要满足条件

图11 半圆形末端组件示意图Fig.11 Schematic of components with semicircular ends

为了便于计算,将组件长度l1和l2统一用l表示.

构建的含有半圆形末端的组件拓扑描述函数模型可以被描述为

采用式(14) 可实现组件半圆形末端形状.图12绘制了半圆形末端的等厚度组件形状,从图中可以看出,该组件具有r=0.3 的半圆末端,其中l=0.6,t1=t2=0.3,两个末端圆心坐标分别为(0.4,0.5)和(1.6,0.5).图13为不同变量取值下获得的形状多变的半圆形末端组件.从图13 可以看出,通过式(14)可有效提升组件构建拓扑几何模型的能力.

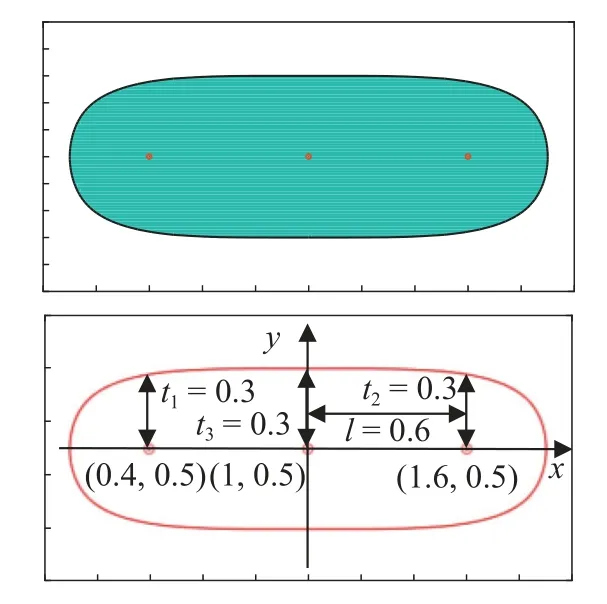
图12 等厚度半圆形末端组件Fig.12 Component of equal thickness with semicircular ends

图13 不同变量取值的半圆形末端组件Fig.13 Components of semicircular ends with different variable values

3.2 最小尺寸精确控制的多变形组件拓扑优化

为了实现通过组件厚度变量设置对结构最小尺寸精确控制,本小节提出增强组件末端连接的局部约束函数.令i和j是设计域内的任意两个组件,(xin,yin) 与(xjn,yjn) 分别为组件的两端半圆圆心坐标,其中n=1和2,1 表示组件的一端,2 表示组件的另一端.位于不同组件中的两个末端圆心坐标间距离可以表示为

距离约束函数可被表示为

式中,τ 是设定的一个阈值,取较小的正数0<τ ≪1.

当拓扑优化过程中满足组件的距离约束函数时,构件的最小尺寸控制可通过设定组件厚度变量的下限轻松实现,即

结合结构尺寸约束,以J为目标函数的最小尺寸约束的拓扑优化模型可被描述为

式中,J(R),ϑk,k=1,2,···,M分别是目标函数和约束函数(如材料体积约束和最小尺寸约束等);uR是设计变量向量R所属于的集合.

在最小尺寸约束下柔度最小优化问题可被描述为

式中,R表示设计区域;Ri,i=1,2,···,N表示第i组件设计变量所组成的向量;J为结构最小柔度,与刚度最大化相一致;f,u,t,ε 分别为实体材料的体力密度、实际位移、纽曼边界 Γt上的面力和二阶线性应变张量;为狄利克雷边界Γu上规定的位移;υ表示满足的试探位移场,符号H=H(x) 表示Heaviside 函数;φS(x;R) 表示整体组件的拓扑描述函数集;q为整数,通常取2;E=Es/(1+v)·{Π+vs/[(1-2vs)δ⊗δ]}为各向同性的弹性张量,E和v分别为实体材料的弹性模量和泊松比,Π和δ分别为四阶单位张量和二阶单位张量,为实体材料的体积的约束上限值.

4 数值求解

在本文中,采用欧拉网格和拓扑描述函数来计算每个节点,同时将虚拟材料模型应用到了FEM 分析中,每个单元的材料杨氏模量表达式为

式中,E0为单元材料的杨氏模量,H为正则化的(Heaviside 函数

式中,σ为正则化参数,a取0.001 防止奇异解的发生.第i个单元的刚度矩阵可以通过获取每个单元的杨氏模量得到

其中,ks为单元的刚度矩阵,与组件占有材料的多少无关.

由于组件中的设计变量可以被精确描述,目标函数的敏度值计算与文献[16,39]中求解相似,在本文中将不再对其进行详细讨论.构建的半圆形末端多变形组件中g(y′) 对应的变量敏度值可以被表示为

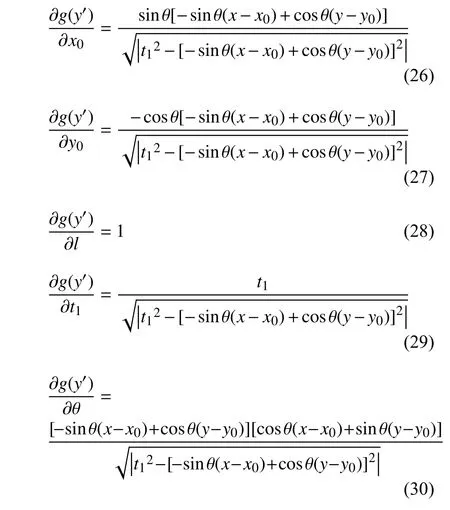
此外,约束函数的敏度值可以利用已经成熟的计算几何算法和有限微分法快速计算获得.

5 算例验证

5.1 悬臂梁算例

基于SIMP和MMC 混合拓扑优化,采用构建的半圆形末端组件对图6 中的悬臂梁进行优化,并与相同组件数量下的MMC 优化对比,MMC 初始设置参数为ini_val=[2.5,1.5,1.2,0.1,0.12,0.1,0.5].两种方法拓扑优化过程如图14和图15 所示,目标函数和约束函数的收敛过程如图16 所示.

图14 基于组件映射结果的悬臂梁优化过程Fig.14 Optimization process for the cantilever beam based on components mapping results

图15 悬臂梁MMC 拓扑优化过程Fig.15 Topology optimization process of the cantilever beam using MMC

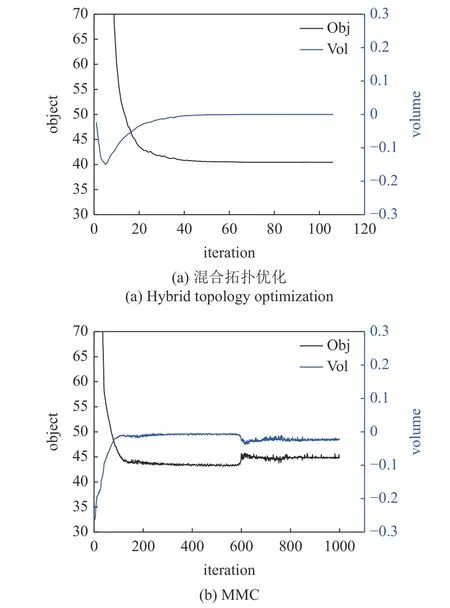
图16 悬臂梁不同方法优化过程的收敛历史Fig.16 The iteration history of the cantilever beam using different methods

由图14和图15 可知,采用混合拓扑优化得到了组件间完全连接的拓扑构型,如图14(a)和图14(b)所示,最终优化的到结构与图3 基本相同,如图14(d)所示,同时结构具有更精确的几何信息.采用MMC得到的优化结果与图3 略有不同,结构内部出现了一些未完全填充材料的空洞区域,如图15(d) 红圈区域所示.这是由于MMC 对初始组件布局依赖性造成的,当给定的组件数量受限时,一些组件会因定位不精确而被过早的视为结构的主承力件,影响其余组件的布局,如图15(b)和图15(c) 所示,最终导致优化结果不能得到相对合理的拓扑构型.

从图16 的收敛历史可以看出,在MMC 中,受组件初始布局的依赖性,初始拓扑构型一直未能确定,导致力的传递路径在优化过程中不断发生变化,引起收敛过程发生明显震荡行为.采用混合拓扑优化方法对悬臂梁进行优化,得到目标函数值为40.44;MMC 在设定的最大迭代次数1000步内并未收敛,最终得到目标函数值为44.75.

依据式(22),以悬臂梁为对象,对本文提出最小尺寸控制方法进行验证.组件的厚度变量下限分别设定为0.08,0.10和0.12,对应的结构最小尺寸分别为0.16,0.20和0.24.优化结果如图17 所示.由图17可知,随着组件最小厚度变量的增大,结构的最小尺寸也在不断的增加.

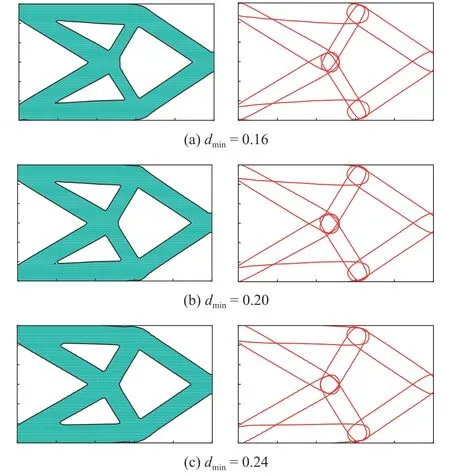
图17 不同最小尺寸约束下的悬臂梁混合拓扑优化结果Fig.17 Hybrid topology optimization results of the cantilever beam with different minimum length scales

与采用TsSC 法在厚度变量为dmin=0.10下的拓扑优化结果相比,如图18和表1 所示.两种方法通过组件厚度变量约束,均实现了结构的最小尺寸控制,但在TsSC 法中,存在因组件间的不完全连接产生的结构边界裂缝现象,如图18 中红圈区域所示.混合拓扑优化方法在实现结构最小尺寸控制的同时,得到了更加完整和光滑的拓扑构型边界,验证了所提方法的有效性.此外,本文所构建的组件拓扑描述函数同时具有形状的可变性,具体细节将在下一个算例中进行详细讨论.

图18 最小尺寸 dmin=0.1 的悬臂梁TsSC 拓扑优化结果Fig.18 TsSC topology optimization result of the cantilever beam with minimum length scales dmin=0.1

表1 不同最小尺寸约束的悬臂梁目标函数Table 1 Object function of the cantilever beam with different minimum length scales

5.2 柔性机构算例

与柔度设计问题相比,柔性机构在保证刚度的同时需要满足结构一定的柔度,该设计问题求解更复杂、难度更大,且优化结果中常常存在结构的单铰链连接现象,是验证所提方法在结构连接性和含约束模型的可制造性常用设计问题.如图19 所示,以输出位移最大化为目标,GA=-Δout/Δin,其中Δin=Finu1in+Foutu2in,Δout=Finu1out+Foutu2out,ujout和ujin,j=1,2,表示在点j施加单位力作用下的水平方向位移.弹簧的弹性常数kout=0.1.已知设计区域被离散为 100×50的单元网格,在输入端施加大小为1 水平向右的载荷,输出端以弹簧模拟工件刚度,体积约束为0.3.

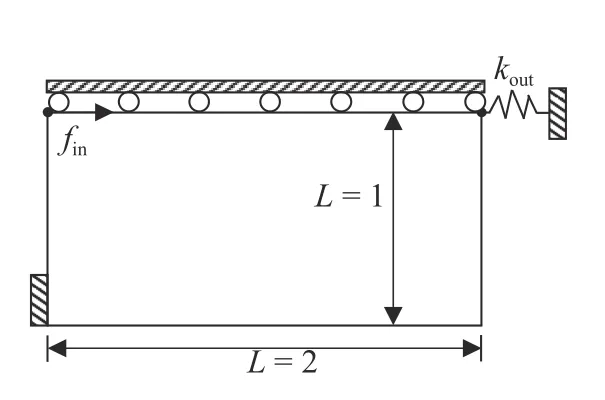
图19 柔性机构示意图Fig.19 Schematic of the compliant mechanism example

在相同组件数量下,分别采用混合拓扑优化方法与初始输入参数为ini_val=[2.3,3.5,1.5,0.1,0.1,0.1,0.6]的MMC 对该算例进行优化,优化过程如图20和图21 所示.由图20可知,在该算例中,采用混合拓扑优化方法同样得到了光滑完整的拓扑构型,优化结果与SIMP 的拓扑优化结果基本相同.同时,由于构建的半圆末端的组件函数拥有组件间完全连接和形状的多变性能力,在构建复杂拓扑构型时也更具灵活性,如图20(c) 所示.而相同组件数量下的MMC 拓扑优化,因其对初始组件布局的依赖性,无法在有限组件数量下找到最优拓扑构型,优化过程中出现了严重的材料缺失和细枝结构,如图21所示.当增加组件数量后,MMC 的柔性机构拓扑优化结果变得与SIMP 结果相似,但仍然存在难以制造的弱连接和细小结构尺寸,如图22 所示.

图20 柔性机构混合拓扑优化过程Fig.20 Hybrid topology optimization process of the compliant mechanism

图21 柔性机构MMC 拓扑优化过程Fig.21 Topology optimization process of the compliant mechanism using MMC

图22 增加组件数量后的柔性机构MMC 优化结果Fig.22 Optimization result of the compliant mechanism using MMC after increasing the number of components

图23为两种方法获得的目标函数和约束函数的收敛历史.从图23 可知,在该设计问题中,由于MMC 对组件布局的依赖,导致在较少组件数量下无法找到有效的传力路径,使得优化过程产生了强烈震荡,在给定最大迭代步内并未实现收敛.

图23 柔性机构不同方法优化过程的收敛历史Fig.23 The iteration history of the compliant mechanism using different methods

针对该算例,采用混合拓扑优化方法,通过对组件厚度变量约束实现拓扑结构的最小尺寸控制,厚度变量下限分别设定为0.075和0.14,对应的结构最小尺寸分别为0.15和0.28.图24为最小尺寸控制下的柔性机构拓扑优化结果和轮廓图.由图24 可知,随着组件最小厚度变量的不断增大,结构中的最小厚度尺寸也在不断的变大,有效避免了优化结果中的单铰链弱连接现象.

图24 不同最小尺寸约束下柔性机构混合拓扑优化结果Fig.24 Hybrid topology optimization results of the compliant mechanism with different minimum length scales

图25和图26 分别为TsSC 法和ECS 法对柔性机构的最小尺寸拓扑优化结果.对比图24、图25和图26 可知,3 种方法优化结果基本相同,但图25和图26 因组件间的重叠或不完全连接,以及初始组件布局的依赖性,导致了结构内部存在浮岛、结构边界不完整和不光滑等现象.图25 中随着对结构最小尺寸的控制,其结构边界裂缝并没有明显变化.本文方法在构建的组件末端完全连接约束下,通过简单的厚度变量调节实现了对整个拓扑结构最小尺寸精确控制,并形成了较为完整和光滑的可制造拓扑优化结构边界.该算例也进一步验证了所提方法的可行性与有效性.

图25 不同最小尺寸约束下的柔性机构TsSC 拓扑优化结果Fig.25 TsSC topology optimization results of the compliant mechanism with different minimum length scales

图26 最小尺寸 dmin=0.02 的柔性机构ECS 拓扑优化结果Fig.26 ECS topology optimization result of the compliant mechanism with minimum length scales dmin=0.02

6 结论

在本文中,提出一种考虑最小尺寸精确控制的SIMP和MMC 混合拓扑优化方法.该方法将SIMP 拓扑优化结果映射为MMC 组件初始布局,并提出半圆形末端形状多变的组件函数模型和组件完全连接的最小尺寸约束拓扑优化模型,通过控制组件的最小厚度变量实现了结构最小尺寸的精确控制.采用最小柔度和柔性机构拓扑优化设计问题验证了该方法的可行性与有效性.与其他方法相比,该方法具有以下优点:(1) 提升了组件构建拓扑构型的能力;(2) 克服了SIMP 拓扑结构边界难提取的问题;(3) 克服了MMC 对初始组件布局强烈依赖问题;(4) 仅利用组件的厚度变量便可实现整个结构的最小尺寸的精确控制;(5) 形成了整体结构相对完整和光滑的拓扑优化结构边界.在本文方法的基础上通过设置组件厚度变量的最大和最小约束,也可同时实现整体结构的最大和最小尺寸精确控制.当前的工作仅对2 维拓扑构型进行了研究,在后续工作中将针对复杂几何形状和三维结构构型提出一种更高效的混合拓扑优化方法.