机器人单足系统沙土跳跃刚-散耦合动力学分析1)
孙昊 刘铸永 刘锦阳
(上海交通大学船舶海洋与建筑工程学院,水动力学教育部重点实验室,上海 200240)
引言
机械系统与散体间的接触在近年来受到越来越多的关注,如探索太空时探测器在外星体表面的着陆、仿生机械在颗粒场上的运动等等.以“探月计划”为例,随着人类的脚步逐渐踏入太空,未来的太空科学任务将大量地涉及在太空飞行或行星探索的过程中收集、存储和返回某些样本材料.为了这些样品的采样和返回任务可以顺利开展,需要设计可靠的在沙土上顺利完成运动并与沙土碰撞的车辆[1-3].有别于传统履带式探测车,近年来跳跃式探测车逐渐受到研发人员的重视[4-7],跳跃式探测车在设计上有小而轻的优点,可以进一步控制设计尺寸,而如何提高其跳跃性能和避障减震能力是其进一步发展的重点之一.这就需要进一步研究探测车在跳跃行为中受到来自沙土的耦合阻力,对这种沙土撞击耦合的动力学响应的理解将为车辆设计提供更多的鲁棒性,并提高整个系统的可靠性.在诸多研究中,机器人单足系统的简化模型被应用于颗粒介质和机器人的动力学耦合特性研究实验中[8].
为了更好地理解散体与机械的耦合效应,对散体颗粒物质的研究不仅需要实验的观测记录,又需要细观机理的准确分析.颗粒材料,也称为散体介质,是由数目庞大且相互作用的离散宏观固体颗粒组成的多相体系,它在自然界中以人们一般认识的沙土为主,是除了流体以外最广泛存在的一种物质形式.目前对散体研究取得的进展包括耗散颗粒气体、离散元理论、颗粒团混合与分级、振动机理等方面[9-10].与传统连续介质的模型不同,散体颗粒虽排列紧密,但颗粒呈现的却是以接触力链彼此连接形成的空间网络.散体动力学具有如下特殊性质[11-12]:(1)只有剪应力达到一定阈值,颗粒才会产生流动,这区别于流体剪应力与流速梯度相关的情况,表明了散体与流体的一定差异[13-14];(2)散体材料的屈服应力常常与流动变形的时间历程相关,并且当散体应变率发生改变时,屈服应力也会相应改变;(3)散体间的摩擦力会令散体颗粒产生显著的剪涨效应;(4)颗粒在流动时,它的黏性系数不是保持恒定,而是与边界层剪切率紧密相关的函数.如何表征颗粒材料的力学性能不但是力学学科重要的前沿基础科学问题,而且有着重要的工程应用前景.
为了将复杂的散体理论与快速发展的计算技术适配,诞生了将传统的连续型土壤化为一定形状的颗粒集群进行计算的离散元(discrete element method,DEM)仿真技术.目前在对大规模的颗粒场进行快速接触检测、将复杂的散体理论等效为利于计算的接触模型、引入颗粒间范德华力、高温场、非球状颗粒、柔性颗粒等更多样的微观模型[15-20]等方面,都不断取得突破.采用DEM 进行仿真,首先需要对颗粒场物性参数进行标定,这就需要对工况进行一定的预判断,选择合适的散体颗粒接触模型.完成了颗粒场的建模后,在对刚散耦合的动力学研究中,需要基于实物实验和仿真分析进一步得到适合快速计算的简化力学模型,来表征物体在侵入颗粒场时的阻力效应,对此国内外有非常多的研究,包括颗粒场的阻力形式研究[21]、基于准静态侵入沙土研究阻力的类流体静压效果[22-25]、基于传统土力学连续土体破坏分层受力分析[26-28].其中基于Poncelet 公式的拓展研究犹为丰富[29-33],这依赖于Poncelet 公式简洁的形式和较好地反映真实动力学效应.
本文采用离散元法模拟颗粒场,以及采用多体动力学方法对机械系统进行建模,对机器人单足系统在颗粒场跳跃问题进行耦合动力学仿真,分析了接触面积、机器人足底形状等不同足部设计对于机构受到颗粒场侵入阻力的影响.研究发现Poncelet定理在描述动态的足部下压颗粒场的过程中能大致地符合阻力变化,但仍存在一定的误差,尤其是在下压深度较大处存在收敛性较差的问题.因此基于经典土力学Prandtl-Reissne 理论,从颗粒场受压分层的形式和动量传递出发,对动阻力项进行修正,提出了修正的Poncelet 公式.通过与刚-散耦合动力学仿真结果比较,说明所提出的修正公式能更准确地计算机械系统在颗粒场上的动力学响应,尤其在达到一定侵入深度后,相较于原始Poncelet 公式,修正公式计算的侵入阻力体现出和仿真结果一致的收敛性.本研究将为新型探测器在行星土壤上运动的系统设计提供动力学建模理论和技术支撑.
1 跳跃模型与刚散耦合理论
1.1 单足系统的跳跃建模
为了探索离散元仿真技术在定量研究机械系统与散体的动力学耦合效应中如何发挥作用,设计了一个弹簧单足机构研究其颗粒场上的一维跳跃运动[34].在过往的研究中往往基于传统土力学转静态侵入沙土[26]、或是纯粹的实物实验设计分析[34].而从离散元仿真角度对于这种机器人单足系统与沙土环境的耦合效应进行动力学仿真值得进一步探索.
由于机械足与颗粒场的动力学耦合效应体现在机械腿足部对颗粒场的侵入阻力,所以在仿真上忽略除足部外其余结构的设计,选择将模型简化为“机械腿杆身-驱动电机-弹簧阻尼器-机械腿足部”的单足系统,如图1(a)所示.为了使单足系统能在颗粒场上较好地完成跳跃动作,经过测试后设计了驱动电机在机械腿杆身上进行位移驱动,当单足系统在颗粒场上静止稳定后,令电机快速沿杆身向上运动,从而令杆身向下压缩弹簧阻尼器,积蓄跳跃所需的弹性势能,这时机械腿足部受到弹簧的向下压力,对在静止稳定的状态下进一步侵入颗粒场,受到来自颗粒场的侵入阻力.当弹簧基本达到最大压缩量、且由于自身刚度效应开始反弹时,电机开始沿机械腿杆身向下运动,使得杆身在大地基上向上运动,并使得弹簧阻尼器充分释放,从而令单足系统高高跳起,从而完成整个跳跃动作.为了提升电机的驱动效果,设计电机为铁质,而机械腿足部和杆身设计为铝制.单次跳跃中机械腿杆身、电机、机械腿足部在竖直方向的位移如图1(b)所示.

图1 单足机器人系统建模[34]Fig.1 Single-leg robot system modeling[34]
1.2 散体接触模型
离散元方法的出现使得可以在更小的尺度应用颗粒间接触的力学理论.颗粒的接触理论可以大致根据干湿性分为有黏与无黏两种[35].无黏颗粒的计算理论相对简单,适合快速计算.而在实际表征沙土颗粒的性质时,为了更好地还原颗粒场受到剧烈冲击后的破坏情况,也往往需要考虑颗粒间由于表面材质或者小分子范德华力带来的黏性作用.
如图2 所示,本文采用Hertz-Mindlin(no slip)接触模型和Hertz-Mindlin with JKR Cohesion 接触模型来分别针对无黏接触和有黏接触,后者在前者的基础上加入表面凝聚力来反映颗粒间的范德华力[35].

图2 颗粒间接触形式:(a)无黏接触,颗粒接触区域受挤压变形;(b)有黏接触,颗粒接触区域受挤压表面粘连Fig.2 The contact forms between particles.(a) Non viscous contact:the particle contact area is extruded;(b) viscous contact:the particle contact area is adhered by the extruded surface
Hertz-Mindlin(no slip)接触模型用于高效计算干沙类颗粒材料.颗粒间的接触力分为法向弹性力、切向弹性力、法向阻尼力、切向阻尼力,表达式如下[35]

Hertz-Mindlin with JKR Cohesion 接触模型在Hertz-Mindlin(no slip)理论上引入了带表面能量密度的修正,适用于有湿度的泥土颗粒.由于接触面在黏性效应下发生变化(见图2(b)),法向相应的修改如下[35].
颗粒间引入黏能Δγ,有
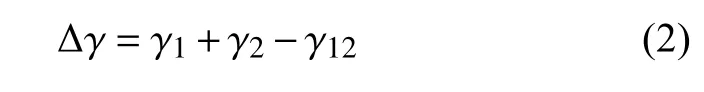
其中,γ1和γ2分别为两颗粒的表面自由能,γ12为界面能.
颗粒受到的外部载荷为Fn,则由于黏性接触导致的接触面半径a的修改形式为

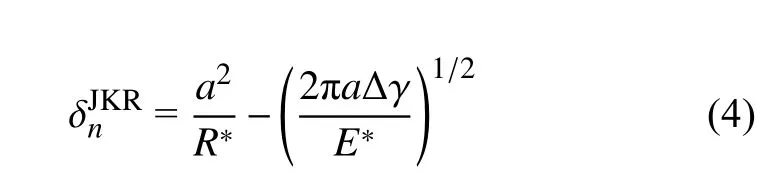
基于新的法向重叠量更新了法向外载荷Fn后,表面黏性力导致的等效法向载荷Fn,JKR为

由于黏性效应,两颗粒在分开时,促使颗粒表面分开的最大分离力的计算公式为

有黏接触的两颗粒间切向力的修正同样类比于法向力修正,在此不再赘述.
1.3 刚-散耦合动力学方程
对于散体与刚体组成的耦合系统,除了刚体系统自身可能存在的弹簧力、阻尼力外,还有散体系统带来的外力和外力矩,以及其他外载荷.在离散元计算中,通过接触理论计算得到散体和刚体之间的作用力,加入各自所受的合力与合力矩中,再同时更新刚体和散体的速度和加速度信息,而后更新位置并进行下一步迭代.在DEM 计算大尺度物体与大数量级散体颗粒间的接触作用力时,为了提高计算效率,会将复杂的颗粒间接触模型简化为弹簧阻尼系统,将颗粒间法向和切向的重叠量作为表征弹簧力的压缩量,将接触理论归并到切向与法向的刚度系数和阻尼系数的计算中去.
根据牛顿-欧拉方程,对于单个颗粒,有

其中,下标i和j为发生接触的颗粒编号,下标rigid 表示与颗粒接触的刚体.Fnij和Ftij为颗粒间接触的法向和切向作用力.Fbni和Fbti为颗粒对刚体的法向和切向作用力,Fk为刚体所受弹性力,Fc为刚体所受阻尼力,Ft为刚体所受其余外界约束力和载荷,m和J为质量阵和转动惯量阵,r和ω为位置坐标阵和角速度阵,Mi和Mrigid分别为单个颗粒和刚体所受的包含接触力在内的所有外力产生的力矩矩阵.
对于本文所研究的机器人单足系统一维跳动刚-散耦合系统,基于速度变分原理,单足系统动力学方程为

其中,q和为单足系统在一维竖直方向上的位移和加速度阵; Φ为约束力阵,主要项为单足系统杆身和电机之间的位移驱动约束; λ为拉格朗日乘子阵;质量阵M和外力阵Q具体如下
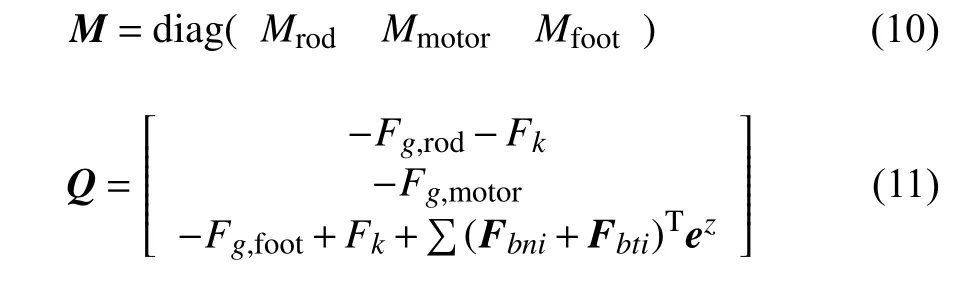
其中,下标 r od,m otor,f oot 分别代表杆身、电机、足部;Fg为重力项;Fk为杆身和足部之间的弹簧力元项;为了简化为竖直方向一维运动,仅考虑颗粒对足部的侵入阻力Fbni和Fbti的竖直方向分量.
2 Poncelet 公式修正
1.3 节完整的刚-散动力学模型往往运用于有限元或离散元的仿真过程中,而在一些追求更高效快捷的情况下,往往需要一个简洁而统一的定律来反映物体侵入沙土介质中所受的阻力,为此,Poncelet等给出了如下表达式[23]

其中,z是物体相对于颗粒场表面的侵入深度,v是物体的速度,k和b被认为是仅仅取决于产生接触的颗粒介质和侵入物体的物性参数的常数.由此,便可以将物体所受的颗粒场阻力Fdrag分解为一个侵入深度相关的类库仑摩擦项(Fdrag,st=-kz)和一个侵入速度相关的类惯性力项(Fdrag,dy=-bv2),这同样可以类比于流体受力分析[15],有着较好的物理解释.
本文选择横截面直径20mm、高6 mm 的足底作为测试工况进行分析,根据Poncelet 公式可以得到颗粒场阻力与侵入深度、足部速度的关系系数.可以看出,在起跳下压颗粒场时,足部受到弹簧阻尼器的脉冲力和颗粒场逐渐增大的侵入阻力产生了一个先加速后减速的变化.若采用Poncelet 公式进行计算,对侵入过程能基本吻合,但在初始加速阶段和减速结束阶段,存在较大偏差.
结合离散元仿真颗粒场受压分层的演化,并根据经典土力学Prandtl-Reissne 理论,受压土体可分层为足底固结区域、过渡区域、被动区域(见图3),其中足底固结区域与足底保持相同的速度向下共同运动.可以认为用Poncelet 公式产生的偏差是由于以足部底端的固结区域颗粒为主的颗粒场分层演化导致的,这部分颗粒的体积随着足部下压而逐渐生长直到成型,从而对颗粒阻力的动阻力项Fdrag,dy=-bv2带来了影响.
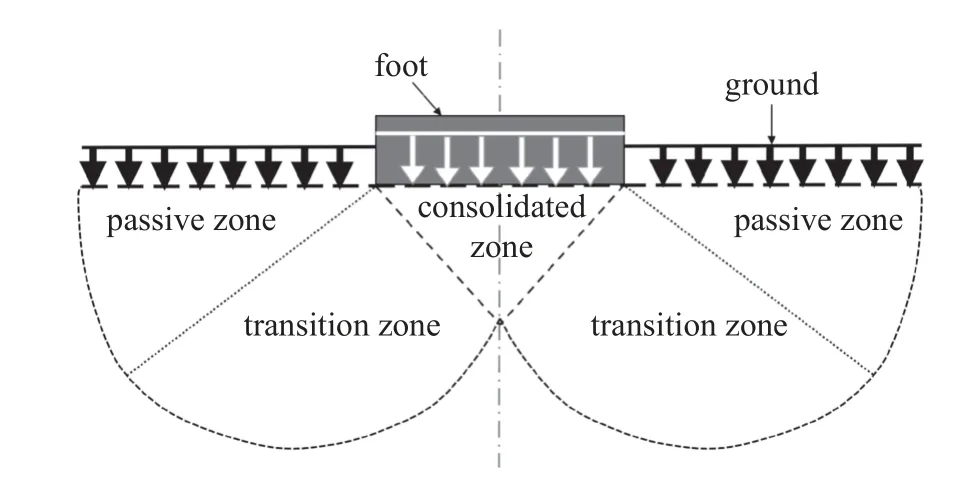
图3 Prandtl-Reissner 理论足底下压颗粒场时颗粒场分层示意图Fig.3 Schematic diagram of soil stratification under pressure of downforce process based on Prandtl-Reissner theory
为了更精准地描述动阻力项的变化,需要对动阻力项进行进一步修正:由于颗粒场受挤压而发生运动,对足部产生了上述动阻力,即(下标gra表示沙土颗粒,mgra表示单个颗粒质量);而颗粒运动产生分层后,动量集中在足底固结区域以及周围过渡区域的颗粒上,其中足底固结区域与机械腿足部速度基本一致,可直接用足部的运动信息去近似描述.故而颗粒场的动量可以用足底固结区域颗粒场动量乘以一个近似系数去描述,即
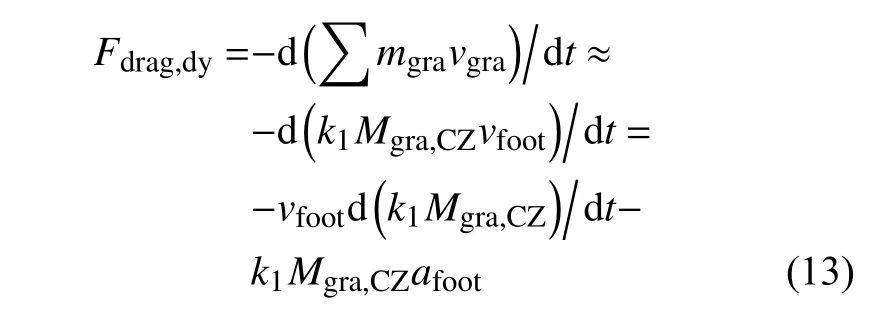
式中,Mgra,CZ表示足底固结区域的颗粒质量之和;k1为产生运动的整体颗粒场动量与足底固结区域颗粒场动量的比例系数,afoot为机械腿足部的加速度.
下压过程中足底固结区域逐渐生长,假设固结区域的体积与下压深度在跳跃这一行为下呈正比,则有Mgra,CZ=k2z,因此进一步可得

从而将颗粒场的运动与足底的运动建立近似的线性关系,用足底运动的相关物理量来表征颗粒场动量损失.这里区分b1和b2的目的是考虑到颗粒场质量等效带来的偏差,需要增加一个系数自由度去更好地贴合真实侵入阻力,可以大致认为b1=b2.式中的项就是Poncelet 公式中的动阻力项,而b2hafoot项就是增加的动阻力修正项.因此修正后的Poncelet公式完整表达式为
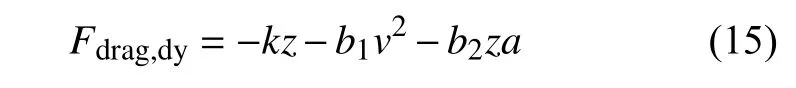
利用修正的Poncelet 公式对测试工况的动力学响应进行计算(见图4 红线所示修正PonceletFdrag),可以发现修正后的侵入阻力与各力学指标的关系都与离散元仿真结果几乎完全吻合,从而验证了所提出Poncelet 修正公式的有效性.且系数b1=9.07 kg/m,b2=9.49 kg/m,有b1≈b2.直接测试b1和b2相等下的动力学响应效果(见图5(a)),基本与修正Poncelet 公式及离散元仿真结果一致,有b1=b2=9.35 kg/m,验证了修正公式推导的可靠性.通过对多个工况仿真计算结果,说明今后可近似使用b1=b2来简化模型.


图4 Poncelet 公式修正前后沙土阻力对比Fig.4 Comparison of dynamic response using modified Poncelet formula or not
对比不同工况下修正后Poncelet 公式计算侵入阻力的结果,对系数k,b1,b2进行初步分析,发现不同工况下的b1和b2会在同一个数量级下产生一定浮动,对足部尺寸和质量具有依赖性;而k在不同体积的足部工况下则基本不变,而在不同足底横截面积下大致呈线性关系(见图5(b)).这表明对于相同形状的机械腿足部和相同颗粒场,具有近似相同侵入阻力的静阻力项系数k.对于不同横截面积的足部,存在关系

图5 修正Poncelet 公式参数分析Fig.5 Parameter analysis of modified Poncelet

图5 修正Poncelet 公式参数分析(续)Fig.5 Parameter analysis of modified Poncelet(continued)
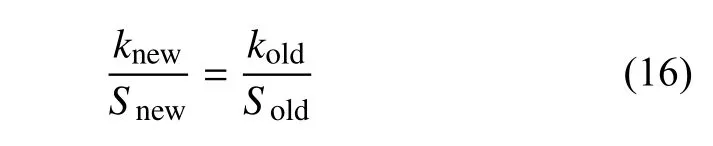
若在低速运动下忽略动阻力项而直接使用静阻力项进行计算时,这一系数转换关系将带来很大的方便.
3 足部设计的动力学分析
机械腿足部在弹簧压缩阶段,会同时受到弹簧阻尼器的压力和颗粒场侵入阻力,由于弹簧阻尼器的力更多依赖于机械系统激励力(即电机驱动机械腿杆身运动后对弹簧的压缩)、且足部在颗粒场上的位移变化为小量.故在压缩阶段,弹簧压力呈现出一种较为均匀的单波峰简谐力形式.而机械腿足部在压缩阶段侵入沙土时,由于自身相当于受到可变性颗粒场不完整约束的弹簧振子,故而速度特性呈现出一种振动效应,这种振动效应也对应地使得颗粒场的侵入阻力出现波动.而颗粒场随着足部运动的受压缩变形,可以分为四个阶段:(1)足部刚开始压缩沙土,固结区开始出现(固结区即经典土力学分析中沙土受到破坏后,固连在足部底端、与足部具有相同速度的颗粒场区域);(2)足部压缩速度最大处,固结区基本生长成型,固结区附近的过渡区(即颗粒运动速度介于足底固结区和周围静止区域间的颗粒场区域)可以明显地看到;(3)弹簧提前开始释放,沙土逐渐密实,足部下压速度开始下降;(4)电机结束下压驱动,沙土不再进一步变形,单足系统机械腿足部开始起跳,与颗粒场分开.
下面进一步分析颗粒场对单足系统的侵入阻力对于足部设计的依赖性,以及由此带来的跳跃效果的差异.首先,分析足部与颗粒场的接触面积的影响,为此设计了相同质量、不同横截面积的一系列圆柱形机械腿足部,直径分布从10mm 至25 mm,接触面积变化幅度约为600%.若是在硬地面上,由于弹簧阻尼器两端的杆身和足部质量均无变化,在相同驱动下,跳跃高度基本不受足部形状的影响.而在可变性颗粒场上,跳跃高度与足部尺寸呈现出对数型依赖关系(见图6(a)),当足部直径为30mm 时,跳跃高度为30.9 mm,足部直径为25 mm 时,跳跃高度为45.4 mm,变化幅度约为50%,跳跃效果受到了极大的影响.从颗粒场变形的角度来分析机理,当足部的横截面积增大时,足底沙土固结区域的体积也随之增大,需要足部施加更多的动量来进一步压缩沙土,从而使沙土呈现出一种更紧实、更“刚性”的动力学效果,表现为沙土达到最大压缩效果的用时更短(见图6(b)),且沙土下压深度减小(见图6(c)),并且可以注意到足部下压颗粒场的深度与接触面积呈现出良好的反比例关系,即下压深度与横截面积成反比h∝1/S.
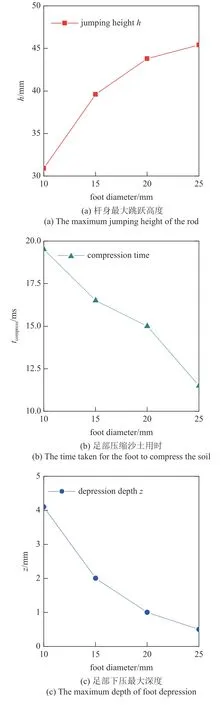
图6 足部直径与各动力学响应指标的关系Fig.6 The relationship between the foot diameter and each dynamic response
为了分析足部的质量效应在跳跃过程中的影响,设计一系列相同横截面积不同高度的同材质圆柱形足部(直径20mm,高度为5~ 10mm 分布).在压缩沙土阶段,选择足部速度最大的时刻展示,此时足部下压速度约为0.1 m/s,观察此时颗粒场的纵向速度分布(图7(a)),可以明显看出,足底与机械腿足部速度基本相同的红色固结区域大致呈现圆锥形,且锥角约为45°,在不同质量的足部下基本保持一致,且绿色过渡区域的变化梯度基本一致,由此可以认为在相同横截面积的平面足部压缩下,沙土的受力分层更多与本身物理性质有关.同时观察机械腿足部在这一阶段的速度变化(见图7(a)),足部速度的波形和最大速度基本一致,但振动频率随着足部质量增大而逐渐减小,呈现出类似弹簧振子系统的动力学特性.
单足机器人在颗粒场上的跳跃行为会引发足底和颗粒场间的振动效应,进行动力学建模分析具有较高复杂性,采用ADAMS和EDEM 联合仿真多体系统和离散元的刚-散耦合效应在目前具有更高的准确性.为了分析足部的形状设计在跳跃过程中的影响,设计一系列相同横截面积不同锥角的同材质圆锥底足部(直径20mm,上半部高度为5 mm,下半部圆锥与水平面夹角在0°~ 50°分布).在压缩沙土阶段,选择足部速度最大的时刻展示,此时足部下压速度同样约为0.1 m/s(见图7(b)).观察发现,虽然锥形足底更利于破开沙土,但足底红色颗粒场固结区的形状并没有太多变化,只是一部分被锥形足部所替代,这也与经典土力学计算中连续体沙土受剪力分层的情况一致,进一步论证这种分层更依赖于沙土本身物理性质;而当足底与水平面锥角过大(图7中45°和50°倾角所示),达到甚至超过了颗粒场固结区域本身的体积时,观察到足底表层只会附加一层速度大致相近的颗粒层,更多的颗粒区域是直接被锥形足底所破开,此时可以认为足底固结区完全被锥形足部取代.沙土破坏分层的改变,反应在足底受力后的速度波动上(见图7(b)),则是足底速度的波动频率并没有和圆柱形足部一样,随着足底的质量增加而减小,当圆锥水平倾角超过35°时,速度的振动频率反而随着质量增大产生一定增大,振动特性出现异常.

图7 颗粒场分层和足部在压缩颗粒场阶段速度变化Fig.7 Stratification diagram of the particle field,and foot velocity variation in the stage of compressing particle field
结合足底的质量效应和形状设计来分析足底设计对跳跃效果的影响(见图8),可以观察到,当足底在整个系统中的质量占比较小时,杆身跳跃高度与足底质量呈良好的线性关系,跳跃高度与圆柱形足底体积的比例系数约为kclin=-6×103m-2,而与圆锥形足底体积的比例系数约为kcone=-7×103m-2.在相同质量的情况下,圆锥形足部的跳跃高度略低于圆柱形足部,这与锥形足部破开沙土取代足底固结区颗粒场有关,可以认为固结区颗粒质量可以进行折算后作为附加质量添加在足部本身的质量上,从而使得圆柱形足部和锥形足部可以有一个进行参照的计算质量对比.当跳跃相同高度时,二者间的体积具有以下关系

图8 杆身最大跳跃高度与锥形、柱形足部体积关系Fig.8 The relationship between the maximum jumping height of the rod and the conical or cylindrical foot volume in the particle field

对于机器人单足系统设计而言,这意味着足底简单的形状改变可以使得机器人在可变形沙土环境中的运动效果发生改变,从而满足不同实际工况的需要.
4 总结
本文以探测器在行星登陆、机器人在沙土上的运动为工程背景,研究了机械系统在颗粒场中的接触动力学问题.采用离散元法和多体动力学方法对机器人单足系统在沙土上的跳跃问题进行耦合动力学仿真.仿真结果表明,若采用Poncelet 公式进行计算,对机械足侵入过程基本吻合,但在初始加速阶段和减速结束阶段存在较大偏差.因此基于经典土力学Prandtl-Reissne 理论,考虑离散元仿真分析足部下压颗粒场的过程中颗粒场的分层和演化,对描述颗粒侵入阻力的惯性力动阻力项进行了修正,提出了一种修正的Poncelet 公式.通过与离散元仿真结果对比,说明所提出修正公式更准确地计算了机械足受到的沙土侵入阻力,尤其是在机械腿足部跳跃压缩沙土的初始阶段和临近最大深度阶段.最后分析了机械腿足部的不同尺寸和形状对沙土中跳跃效果的影响.发现机械腿足部与颗粒场的接触面积会对颗粒场下压深度、颗粒场压缩持续时间、机械腿跳跃高度产生直接的单调的影响.此外,机械腿足部的体积与跳跃高度呈现出良好的线性关系;而同样体积下锥形足部的跳跃高度会低于圆柱形足部.考虑足部形状带来的不同与足底伴随运动的固结区域颗粒场空间有关,给出了锥形足部和柱形足部的体积对跳跃效果近似计算公式.然而,机器人单足系统在颗粒场上的跳跃涉及复杂的振动效应,其振动频率、振幅衰减等动力学响应和单足系统设计、颗粒场物性参数之间的深层联系还需要进一步挖掘.本研究将拓展刚-散耦合动力学理论,并且为新型探测器在行星土壤上运动的系统设计提供技术支撑.

