求解三维流固耦合问题的一种全隐全耦合区域分解并行算法1)

邓小毛 廖子菊

*(广东外语外贸大学数学与统计学院,广州 510006)

†(暨南大学信息科学技术学院数学系,广州 510632)

引言

流固耦合现象广泛存在于自然界及各类工程问题中,如昆虫与鸟类的飞行[1]、血流和血管壁的相互作用[2]、高层建筑、高耸结构及桥梁结构的风致振动[3-4]、飞行器的颤振与运动稳定性[5]以及医疗器械的设计与优化[6-7]等.在工程问题中,由于流场与弹性结构相互作用会诱发许多不良现象(如静稳定性发散、颤振、极限环振荡及涡激振动等),这些现象可能引起结构破坏或疲劳损伤,因此在工程设计与计算中考虑流固耦合作用对于结构安全具有重要意义.

流固耦合涉及到不同物理场的多尺度(时间和空间)非线性耦合,其快速准确求解一直以来都是力学与工程领域的一个难题[8].目前工程上流固耦合问题的求解策略主要分为两类:分区算法和整体算法[9].在分区算法中,流体和固体区域分别独立地进行求解并通过交界面交换位移和作用力等数据,这类方法具备良好的程序模块性,可以直接利用现有的计算流体力学(CFD)和计算固体力学(CSD) 应用软件及程序,且对计算机内存要求较低,是目前流固耦合问题的主流求解方法[10].

分区算法又分为分区显式(弱耦合)算法[11-12]和分区隐式(强耦合)算法[13-14],其中分区显式算法在每个时间步对流体和固体方程只分别求解一次,由于存在时间滞后效应,流固界面上的守恒律无法满足,因此时间步长必须取得非常小,并且数值模拟结果有可能收敛到错误的解上.分区显式算法主要适用于气动弹性等较大质量比的情形[15].分区隐式算法则在每时间步内交替迭代求解各单场方程直至收敛以满足界面守恒,常用的求解方法主要有固定点法[16]、Newton 类方法[17]和优化方法[18].分区隐式算法的这种交替迭代求解方式本质上是一种非线性Gauss-Seidel 型算法,它的收敛速度较慢,并且容易出现不收敛的情况,因此通常需要采用一些加速收敛技术如Aiken 松弛算法[19].此外,当流体和固体的密度非常接近时,迭代耦合方法会出现由附加质量效应导致的数值不稳定性[20].

为了避免分区算法的这些问题,近些年来整体算法逐渐受到越来越多的关注[21-25].整体算法又称全耦合算法,其对流固控制方程以及界面守恒条件同时进行求解,可较好地适应强附加质量效应,以及不会恶化整体系统和各子系统的求解精度.此外,由于比分区算法少了一层迭代,收敛速度相对较快,且更适合并行计算,但其缺点是方程具有极强的非线性,且已失去了子问题控制方程系统矩阵的特点和可利用之处,不能直接利用现有的流体、固体算法和软件,需要重新研究求解算法.文献[26-27]对分区算法和整体算法的计算性能进行了详细比较.

流固耦合问题整体求解的计算规模通常非常巨大,且离散矩阵具有病态性,因而对方程迭代求解技术要求很高,目前已经发展了一些有效的方法(主要是Newton 类方法)用于其离散非线性方程组及相应线性系统的求解[28-29],不过由于三维问题的计算量巨大,并且现有的算法大多缺乏较好的并行可扩展性,难以处理大规模问题的数值模拟,因此目前关于三维问题的数值结果尚不多.

本文将针对三维非定常流固耦合问题,构造一种适合大规模并行计算的整体求解并行算法.对于流固运动界面,我们采用任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE) 方法进行描述[30].对于流体、固体及动网格方程,采用非结构有限元进行统一离散,然后构造一种结合Newton 类非线性求解器,Krylov 子空间算法类线性求解器以及基于区域分解的Schwarz 预条件子[31]的Newton-Krylov-Schwarz(NKS) 算法进行高效求解.NKS 算法在求解大规模线性及非线性方程组时非常有效,已经成功地应用于各类大规模科学计算问题,我们在之前的工作中利用这类方法来构造求解流体动力学方程的并行算法[32-33],在数千核的计算规模中取得了良好的收敛性和并行可扩展性,本文将之拓展到流固耦合问题,通过标准测试算例验证其计算效果,并对算法的收敛性、稳定性、鲁棒性和并行可扩展性等数值性能进行测试分析.

1 控制方程

本文考虑不可压缩流体与弹性体的相互作用问题.下面我们基于ALE 方法给出要求解的流固耦合控制方程及相应的边界条件,对于流体、固体和网格等不同场的变量,我们分别用上标f,s,m来表示区分.

1.1 ALE 描述及动网格方程

其中dm(X,t) 表示网格位移,通过求解给定的网格运动方程得到.为了方便,这里我们采用调和方程来描述网格位移,即有

其中ds表示交界面处的固体位移.除了调和方程,也可以采用其他方程来描述网格位移,例如弹性方程,它对大变形的情况具有更好的适应性,不过与此同时也引入了一些附加的待定参数.我们的测试结果显示,使用调和方程对于一般的变形已经可以得到良好的计算结果.

1.2 流体方程

ALE 坐标下,不可压缩Navier-Stokes 方程可写为

1.3 固体方程

对于固体变形,我们采用线弹性模型,在Lagrange 描述下的弹性动力学方程为

为了方便求解,将式(9)化为如下一阶导数形式

式(1),式(4),式(5),式(10)统一构成流固耦合控制方程组,式(2)～式(3),式(6)～式(8),式(11)～式(12)组成边界条件.

2 数值方法

2.1 有限元离散

针对流固耦合方程,空间方向我们采用非结构有限元进行离散,为此我们首先给出控制方程的Galerkin 变分形式.

对于动网格方程,分别定义如下试探函数空间和测试函数空间

注意流固界面处的位移连续性条件在Vm中作了限制.对于固体方程,类似地定义相应函数空间

注意上式左边第三项利用到了流固界面处的应力连续性条件(12).

最后,对于流体方程,定义函数空间

对于变分式(13)～式(15),采用非结构有限元进行离散,其中网格方程和固体方程采用标准的线性有限元,流体方程采用P1-P1 稳定化有限元[34].通过定义P等函数空间相应的有限元空间,然后将式(13)～式(15)中的测试函数取为线性有限元的基函数,即可得到有限元离散方程.需要注意的是对于不可压缩流动问题,当速度和压力采用等阶的P1-P1 有限单元时,其离散方程不满足Ladyzhenskaya-Babuška-Breezi(LBB) inf-sup 条件,需要添加稳定化项.本文采用流线迎风Petrov-Galerkin(SUPG)方法[35],设流体区域的网格为={K},则流体方程的有限元变分形式改为

通过有限元离散后,我们得到如下半离散形式的非线性常微分方程组

其中y(t)为整个计算区域的所有待求未知量,即由网格位移,固体位移及速度,流体速度及压力一起组成的向量,M为质量矩阵,L(y(t))为除时间导数项外的非线性函数项.注意由于流体区域的网格是随时间变化的,因此这里质量矩阵也为y(t)的函数.

在时间方向,采用二阶BDF 全隐格式进行离散,得

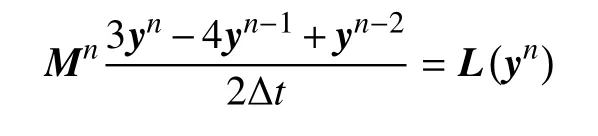
因此在每一时间步,需要求解如下大规模非线性方程组

在启动步中,先采用半步长的隐式Euler 法计算出BDF2 格式所需要的初值.

2.2 Newton-Krylov-Schwarz 并行算法

在每一时间步,需要求解大规模非线性方程组(18).为了高效并行地进行求解,本文构造一种基于区域分解法的Newton-Krylov-Schwarz(NKS) 并行求解算法,主要包括非线性方程求解器、线性求解器和预条件子三部分.为了方便推导,略去上标,将方程组写为一般形式

采用带线搜索的非精确Newton 法来求解非线性方程组(19),假设第k迭代步的值为y(k),则第k+1 迭代步的值更新为

其中步长 α(k)采用线搜索方法[36]来计算,Newton 修正量 δy(k)通过求解如下线性方程组得到

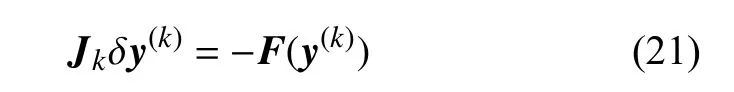
其中 ηk为相对收敛误差,当 ηk→0时,则上述算法退化为精确Newton 法.

对于Jacobian 矩阵Jk,一般可以通过无矩阵化方法[37]或者有限差分方法进行近似求解,也可以通过解析方法精确计算.在我们之前关于流体问题的测试中,采用精确的Jacobian 矩阵可以使算法具有更好的收敛性和鲁棒性[32],因此,本文对Jacobian 矩阵也采用解析表达式进行计算.Jacobian 矩阵的主要计算量为流体方程的非线性对流项及稳定化项,我们注意到在这些项中对网格位移及速度的导数项的量级较小,因此进行了相应的简化处理,即忽略对网格位移及速度的导数,这可以有效降低算法的计算量以及编程的工作量,并且数值测试表明这种处理几乎不影响算法的收敛性.

最后,为了加快收敛速度,对线性方程组(21)进行预条件处理

而限制型加性Schwarz 预条件子则定义为

整个NKS 算法的计算流程如下:

(1) 采用上一个时间步的解作为初始值

(2) 对k=0,1,2,···,执行以下步骤,直至收敛:

①构造F(y(k)) 的Jacobian 矩阵Jk;

② 采用带有预处理的Krylov 子空间迭代法GMRES 求解如下线性方程组

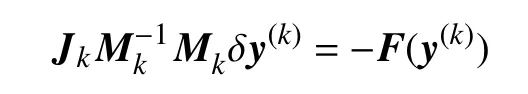
③通过线搜索获得步长 αk;

④ 更新迭代解

3 数值算例与算法性能测试

本节首先采用标准测试算例对本文算法进行验证,然后对算法的收敛性、鲁棒性及并行可扩展性等数值性能进行测试研究.计算平台为国家超级计算广州中心的天河二号集群,其计算节点的硬件配置为双路12 核Intel(R) Xeon(R) E5 CPU@ 2.4 GHz,64 G 内存.算法程序基于PETSc 软件[38]编写,计算网格采用非结构四面体网格,利用CUBIT 软件[39]生成,网格并行分区采用ParMETIS 软件[40]实现.计算过程中,Newton 法的收敛误差限rtol设定为1.0×10-6,最大迭代次数设定为30;线性求解器采用重启型GMRES,相对误差限设为1.0×10-4,重启次数设为400,最大迭代次数设为2000;默认情况下,区域分解的重叠层数设为2,子区域问题采用ILU(2)近似求解.

3.1 算法验证

采用文献[22,28]的弹性障碍物绕流标准测试计算模型,如图2 所示,计算区域为(0,L)×(0,H)×,其中各几何参数分别为:槽道的长L=1.5 m、宽W=0.8 m、高H=0.4 m,内部弹性阻碍物的长l=0.2 m、宽w=0.4 m、高h=0.2 m,弹性体与入口的距离为e=0.4 m ;流体的物理参数为ρf=1.0×103kg/m3,动力黏性系数为 µf=1.0Pa·s ;弹性体的物理参数为 ρs=1.0k g/m3,杨氏模量Es=1.4 MPa,Poisson 比 νs=0.4,相应的Lamé系数为 λs=2 MPa,µs=0.5 MPa.

图2 计算区域Fig.2 Computational domain

入口处给定入流速度

其中s(t) 是一个时间方向的光滑因子,定义为

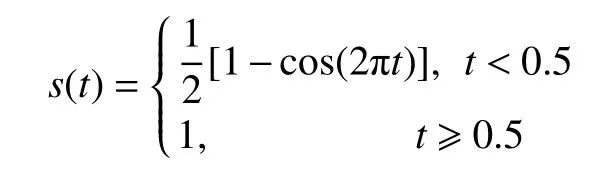
为平均流速,这里取=1.壁面采用无滑移边界条件,出口处采用无应力条件n·σf=0;弹性体的底座处给定Dirichlet 边界条件ds=us=0.

采用四个不同规模的网格进行计算,网格单元数与自由度总数如表1 所示.对于这四个不同网格,分别采用24,48,96,192 个处理器核进行计算,程序的运行内存,Newton 法的平均迭代次数,每Newton 步的平均GMRES 迭代次数,以及平均每时间步的计算时间也同时在表1 给出.

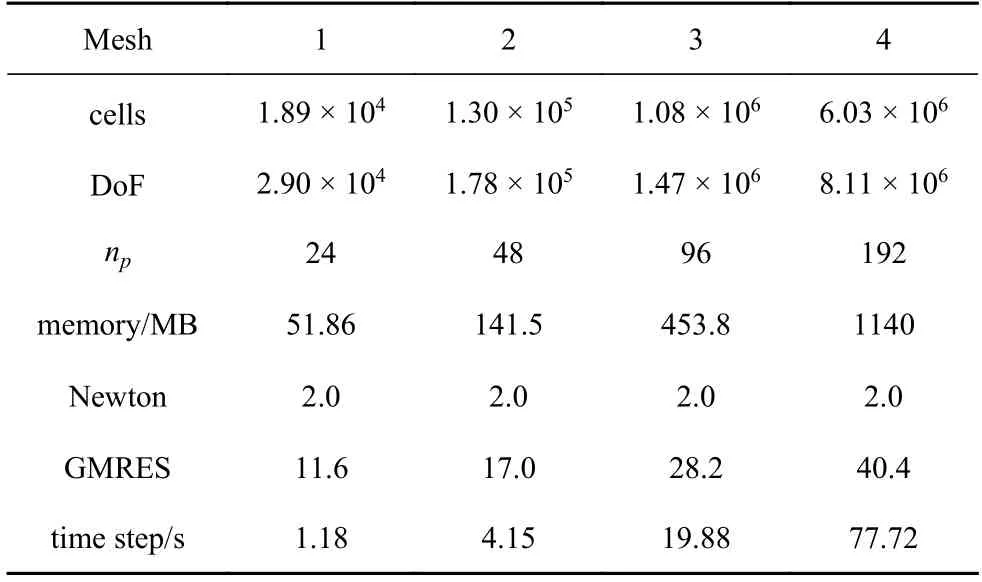
表1 计算网格Table 1 Computational meshes

为了验证数值结果的准确性,我们计算位于弹性体顶点处的两个观测点P1(0.4,0.2,-0.2)及P2(0.5,0.2,-0.2)的位移,并与文献[22]的计算结果进行比较,如表2,3 所示.可以看到本文计算结果与文献结果基本一致,表明本文算法的求解结果是有效和可靠的.

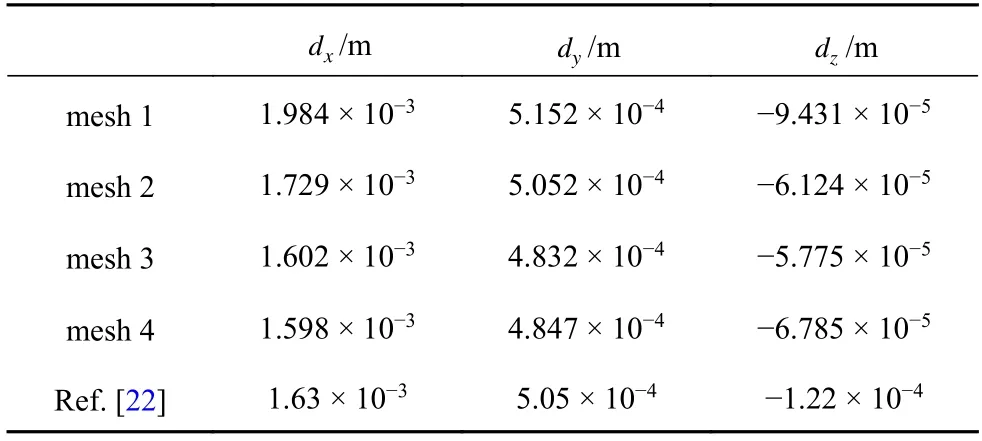
表2 观测点 P 1(0.4,0.2,-0.2) 处的位移Table 2 Displacements at pointP1(0.4,0.2,-0.2)

图3 给出了t=3 s 时的弹性变形及流场速度分布图,为了验证较大变形的情况,我们同时也给出了弹性模量Es=350kPa 及Es=87.5 kPa 的结果.而当进一步降低弹性体的弹性模量时,由于弹性体变形过大,网格出现奇性,从而导致计算发散.注意这种发散不是数值格式不稳定性带来,不能通过减小时间步长来消除.

图3 不同杨氏模量下的弹性变形及速度分布图Fig.3 Deformation and velocity distribution with different Young's modulus

表3 观测点 P 2(0.5,0.2,-0.2) 处的位移Table 3 Displacements at pointP2(0.5,0.2,-0.2)

3.2 算法性能测试

首先对算法的收敛性能进行测试.影响算法收敛性能的参数主要有两个:一是区域分解的重叠层数 δ;二是构造子区域局部预条件子的线性求解器.分别取 δ=1,2,然后采用不同填充级的子区域求解器ILU(k) 进行计算,测试结果如表4 所示,其中Newton 表示平均每个时间步的非线性迭代次数,GMRES 表示平均每个Newton 步的线性迭代次数,Time 表示平均每个时间步的计算时间(单位为秒).可以看到,Newton 迭代次数基本不受影响,表明不同填充级的ILU 线性求解器均可作为子区域问题的求解器.另外,由于填充级增加时,ILU对Jacobian 矩阵的逆有更好的逼近,因此可以看到线性迭代次数显著随之减少.不过每时间步的计算时间并没有相应减少,原因是当填充级增加时,虽然线性迭代次数显著减少了,但是花在子区域预条件子构造的时间相应增加了,因此有个折衷的选择,在本算例中,填充级取为k≤2 均可,当k=3 时计算时间则显著增加.另外,由于本算例中Newton法的收敛速度很快,因此子区域的重叠层数对计算时间影响不大.

表4 子区域的重叠层数及子问题求解器对算法性能的影响Table 4 Impact of the overlapping size and the subsolver on the NKS algorithm

接下来我们考察NKS 算法的稳定性.表5 给出取不同时间步长时算法的收敛性能.由于时间方向采用了全隐离散格式,因此算法具有很好的稳定性,当时间步长Δt从0.001 增大至0.128 时,虽然Newton迭代步数、线性迭代步数和每步的计算时间都略有增加,但总的来说算法仍能快速收敛,表明算法可以在精度允许的范围内自由地选择时间步长进行数值模拟.

表5 不同时间步长对NKS 算法收敛性能的影响Table 5 Performance of NKS with respect toΔt

随后对NKS 算法的鲁棒性进行测试,即考察取不同的物理参数对算法收敛性能的影响.表6给出了仅改变流体黏性系数,而其他参数保持不变时算法收敛性能的测试结果,表7 给出仅改变固体密度时的测试结果,表8 则给出仅改变固体的杨氏模量和Poisson 比的测试结果.可以看到在不同的物理参数下,算法的收敛性能基本保持不变,表明了算法具有良好的鲁棒性.

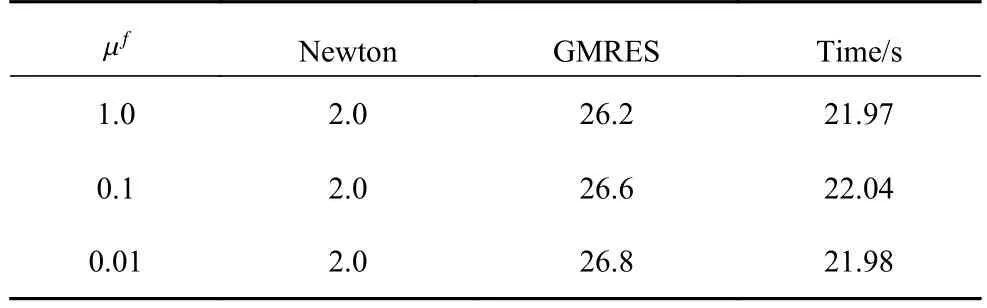
表6 关于流体黏性系数的算法鲁棒性测试Table 6 Robustness of the algorithm with respect to the fluid viscosity

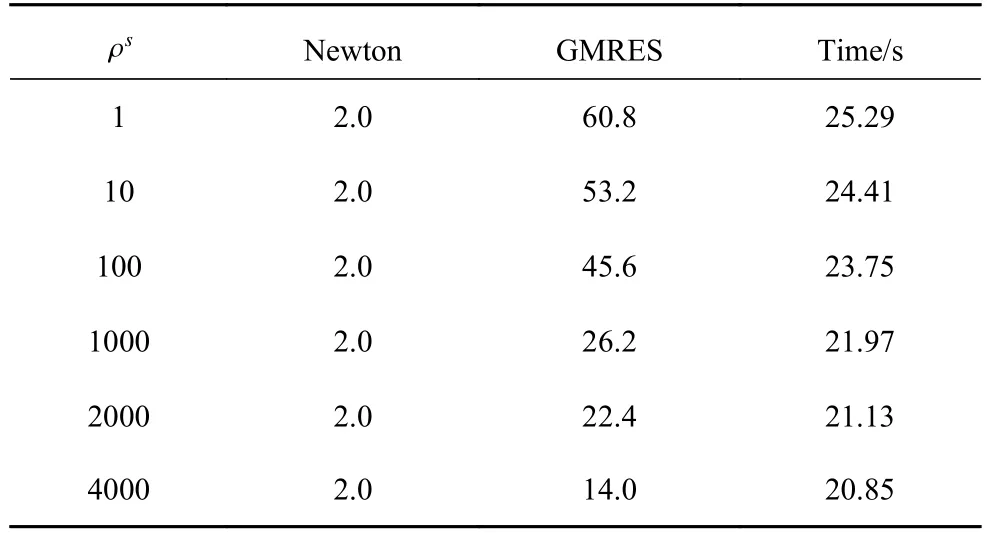
表7 关于固体密度的算法鲁棒性测试Table 7 Robustness of the algorithm with respect to the solid density

表8 关于杨氏模量和Poisson 比的算法鲁棒性测试Table 8 Robustness of the algorithm with respect to the Young’s modulus and Poisson’s ratio

最后,对算法的并行性能进行测试,如表9所示,其中np表示计算的进程数(等于处理器的核数),speedup为加速比,ideal 表示理想加速比,efficiency 表示并行效率.可以看到,随着进程数的增加,非线性迭代次数保持不变,线性迭代次数则略有增加,每迭代步的计算时间则显著减少.当进程数从192 增加到1536 时,算法取得了超线性的加速比,当进程数增加到3072 时,并行效率为91%.算法的加速比曲线如图4 所示,测试结果表明了本算法具有良好的并行效率和可扩展性.

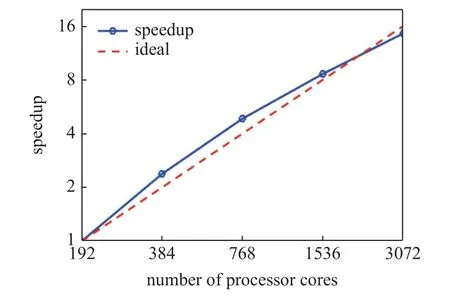
图4 算法加速比Fig.4 Parallel speedup of the algorithm

表9 算法并行可扩展性测试Table 9 Parallel performance and scalability of the algorithm

3.3 与其他算法性能的比较

本节将本文方法与文献中已有的一些算法进行比较.对不同算法的性能直接进行对比是一项复杂的工作,一方面由于不同文献通常采用了不同的测试算例,另一方面算例的计算规模、算法的参数设置以及进行测试的机器也不相同.本文选取平均每时间步的非线性迭代次数作为算法收敛性能的考量,另外,基于不同文献测试算例的问题规模不同,参照文献[29]的做法,我们定义一个时间步内“每CPU 核在每秒钟内所求解的自由度数”这一指标来比较不同算法的计算效率.最后,为了考察算法处理大规模问题的能力,对算法的并行性能也进行对比.关于全耦合算法,目前文献中的测试算例大多都是关于二维问题的,三维算例较少,在我们的检索范围内,找到了文献[22,28-29]这几种不同的数值方法,这几种方法均采用Newton 法作为非线性求解器,Krylov 子空间迭代法作为线性求解器,它们的主要区别在于预条件算子及其求解算法不同,表10给出了本文方法与它们在收敛性能与并行性能方面的比较结果.可以看到,在不考虑算法收敛参数设定以及测试机器的情况下,本文方法每时间步的Newton 迭代次数最少,每CPU 核在每秒钟内所求解的自由度数仅次于文献[28]的方法,在并行可扩展性与并行效率上,本文方法远远高于其他方法,表明在处理大规模问题上具有较好的潜能.

表10 本文算法与其他文献算法的性能比较Table 10 Comparison of different numerical approaches found in literature

4 结论

本文针对三维流固耦合问题,提出了一种有限元数值求解的全隐全耦合可扩展并行算法.为方便处理复杂的计算区域,采用了三维非结构网格进行空间离散,为使算法具有更好稳定性和鲁棒性,采用二阶BDF 全隐格式进行时间离散.对于时空离散后得到的大规模非线性代数系统,构造了基于区域分解的Newton-Krylov-Schwarz 并行算法对流体、固体与动网格方程进行一次性整体求解.采用弹性障碍物绕流问题的标准测试算例对算法的准确性进行了验证.算法性能测试结果表明本文提出的算法在数千处理器核条件下具有良好的并行可扩展性能.通过测试算法在不同计算时间步长、不同物理参数下的收敛性能,验证了算法具有良好的稳定性和鲁棒性.另外,本文对动网格方程采用了较为简单的调和方程模型,数值结果表明其在大变形的情况下计算会发散,为了避免这一问题,可以考虑更复杂的弹性方程模型,这些问题有待进一步深入研究.