泊松白噪声激励下强非线性系统的半解析瞬态解1)

叶文伟 陈林聪,2) 孙建桥

*(华侨大学土木工程学院,福建厦门 361021)

†(福建省智慧基础设施与监测重点实验室,福建厦门 361021)

**(加州大学Merced 分校工程学院,美国默塞德 95343)

引言

自然界和工程中普遍存在的随机激励,根据其概率密度分布规律,可以划分为高斯激励与非高斯激励两大类.截至目前,针对高斯激励的相关研究已经较为深入[1-5].然而,现实中大多数随机激励都呈现出固有的非高斯性质,如公路桥梁上的车辆荷载、地震和火山震导致的地面运动等,仅用高斯激励进行建模往往是不够的.例如,在对系统进行可靠性评估时,若将原本的非高斯激励直接替换为高斯激励,往往可能导致巨大的误差,甚至与客观事实相悖.因此,分析非高斯激励下的非线性随机振动具有重要的意义.

泊松白噪声是一种脉冲幅值与到达时刻均为随机的离散随机脉冲序列.作为一种典型且重要的非高斯激励模型,泊松白噪声常被用于描述在科学和工程中样本函数不连续的随机现象,其动态特性已引起了广泛的关注.当前,针对泊松白噪声激励下系统的动力学分析主要集中于稳态响应的研究[6-10],而对于瞬态响应研究仍较为有限.然而,瞬态响应预测是非线性随机振动研究的重要内容之一,对于结构的可靠性评估也具有重要价值.

当前,预测泊松白噪声激励下非线性系统的瞬态响应的方法主要是蒙特卡罗模拟法[11-12]、路径积分法[13-15]与广义胞映射法[16-17].这些方法均存在一些不足,例如,蒙特卡罗模拟法计算代价较为高昂,尤其模拟尾部概率密度需要大量的样本使其平滑.路径积分法通过对全局转移概率密度的积分式离散化,以路径和替代,这种近似使得计算量较大.广义胞映射法以离散胞之间的映射关系来表征系统中的状态转移,但算法较为复杂,且易因胞流扩张降低方法的准确性.此外,上述方法所获得的解均为数值解,在结构优化设计的应用方面也存在着一些局限性.因此,还需发展新的瞬态响应理论分析方法,以满足工程实际的需要.

作为一种基于函数插值的非迭代算法,径向基神经网络不仅可避免不必要的、冗长的计算,而且具有唯一最佳逼近,收敛速度快等优点.近几十年来,径向基神经网络由于其优越的拟合能力备受学者关注[18-19],并在诸多领域内被广泛应用[20-23].值得注意的是,径向基神经网络在求解各类偏微分方程或复杂非线性方程问题[24-26]上亦展现出极大的优势.最近,有学者创新性地将径向基神经网络运用于求解高斯白噪声激励下非线性系统的半解析瞬态解[27]与首次穿越问题[28],这对推动径向基神经网络应用于非线性随机振动的研究具有重要价值.

本文将径向基神经网络方法进一步用于求解泊松白噪声激励下单自由度强非线性系统的非平稳广义Fokker-Plank-Kolmogorov(FPK)方程.首先,采用含时变待定参数的径向基神经网络构造广义FPK方程的瞬态解;然后,应用有限差分法离散近似时间导数项,再结合随机取样技术构造一个具有时间递推形式的损失函数.最后,时变最优权值系数可通过拉格朗日乘子法使损失函数最小化获得.通过两个经典强非线性系统的瞬态响应分析证实了该方法的可靠性与准确性,并分别给出了相应系统响应随时间演化的规律.

1 理论概述

1.1 广义FPK 方程

考虑一个在泊松白噪声激励下的单自由度强非线性系统,其运动方程可表述为

其中,f(X,) 表示阻尼和恢复力项,gi(X,) 表示随机激励特性,ξi(t) 表示一系列相互独立的泊松白噪声,其形式导数可由复合泊松过程Ci(t) 定义为

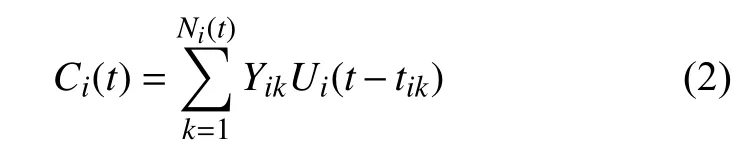
式中,Ni(t)为泊松计数过程,其平均到达率为λi;Yik表示第k个脉冲到达时刻tik的随机振幅,且每个随机振幅Yik与到达时刻tik相互独立;Ui为单位阶跃函数.假设Yik具有相同的对称分布,且均值为零,复合泊松过程增量的j阶矩函数存在下列关系

特别地,当λi为常数且Yi独立同分布时,{C(t),t≥0}为齐次复合泊松过程.此外,当λi趋于无穷时,泊松白噪声近似为高斯白噪声.

令X1=X,X2=,则运动方程(1) 可转化为如下形式随机微分方程

系统(1) 的响应向量X={X1,X2}T的转移概率密度函数p(x,t|x0,t0) 由下列广义FPK 方程支配

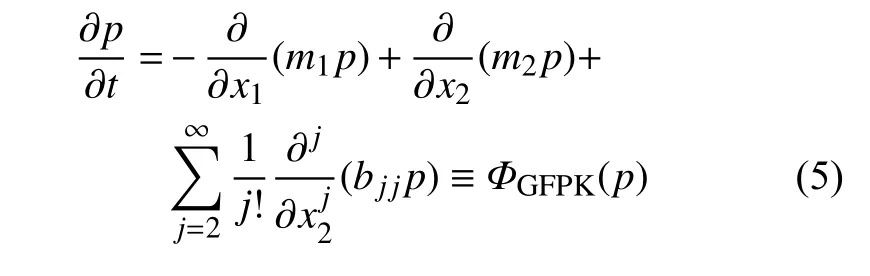
其中,ΦGFPK(·) 表示广义FPK 方程微分算子,相应的系数m1,m2与bjj为

广义FPK 方程(5) 的初始条件与边界条件为

值得注意的是,广义FPK 方程(5) 含有无穷偏微导项,即使是对于简单的线性系统也无法求解,通常需要根据精度要求进行适当截断.在下一节中,将简要介绍径向基神经网络方法求解广义FPK 方程(5)的过程.

1.2 径向基神经网络方法

假设广义FPK 方程(5) 的瞬时解为高斯径向基神经网络形式,即

其中,x=(x1,x2),NG为激活函数的个数,w(k)=(w1(k),w2(k),···,wNG(k)) 是一组时变的待定权值系数,k记为时间步数,时刻t=kΔτ,k=1,2,···n,Δτ为时间步长,Gj(x,μj,σj)为二元高斯函数形式的激活函数,即

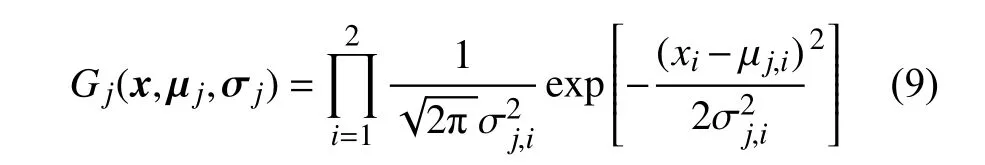
式中,σj=(σj,1,σj,2) 与μj=(μj,1,μj,2) 分别表示第j个二元高斯基函数的标准差与中心.

注意到概率密度函数(8) 与二元高斯函数(9)均满足归一化条件,即

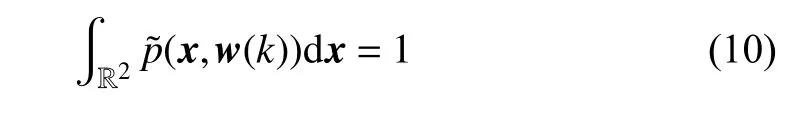
故由式(10)和式(11) 可推导出wj(k) 的约束条件为

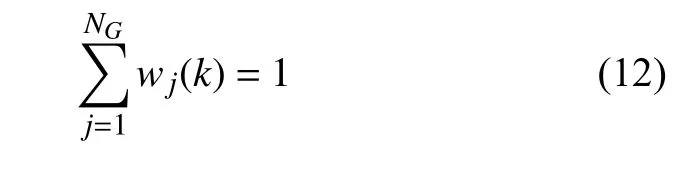
令时间步长Δτ是非常小的量,广义FPK 方程(5) 的时间导数项可采用有限差分法近似,即

其中,εt为一阶有限差分近似的截断误差.将试解(8)和时间导数项近似关系(13) 共同代入到广义FPK方程(5) 中,可得到如下形式的一个局部误差

随后,在有限域ΩS∈ R2内采用取样技术,构造一个损失函数Loss(w(k))

其中,NS为样本点个数.结合约束条件(12),建立一个拉格朗日函数为

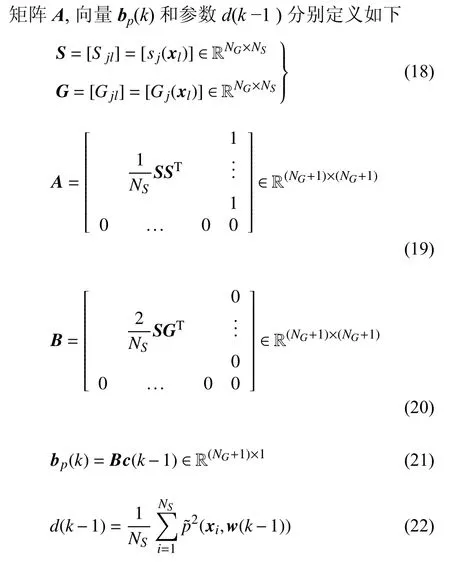
根据拉格朗日乘子法,可知式(17) 最小化的必要性条件为

式(23) 可进一步改写为矩阵形式如下

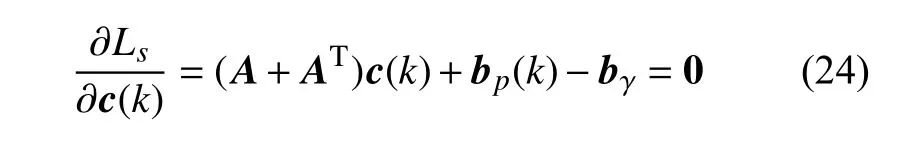
当逆矩阵(A+AT)-1存在,时变的最优权值向量可通过式(24) 获得,即

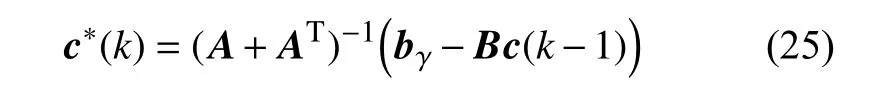
需要指出的是,该逆矩阵(A+AT)-1的存在与否在很大程度上取决于数据矩阵S[29].实践证明当NS≫NG可避免逆矩阵(A+AT)-1的奇异性[28,30].

此外,当限制所有输出的权值系数wj(k) ≥0时,概率密度函数(8) 能够严格保证非负性,这是一个充分条件.在大多数情况下,所获得的wj(k) 是非负的,因而施加约束wj(k) ≥0对概率密度函数解的影响很小.图1 中给出了上述算法的简要流程图.

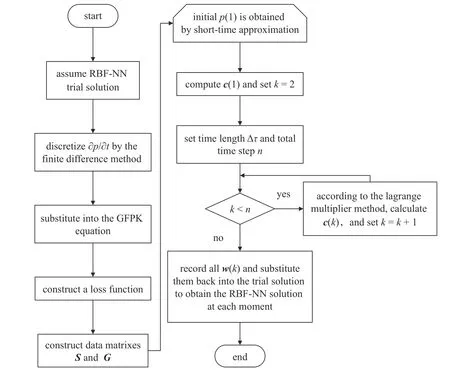
图1 径向基神经网络算法流程图Fig.1 The flowchart of the RBF-NN scheme

2 算例验证

本节将研究两个经典的强非线性系统,来验证上述方法的有效性,其中所采用的蒙特卡罗模拟样本数均为3.0×107.

2.1 双稳态Duffing 系统

考察一个在随机激励下的双稳态Duffing 振动系统[31],其运动方程在状态空间中可表示为

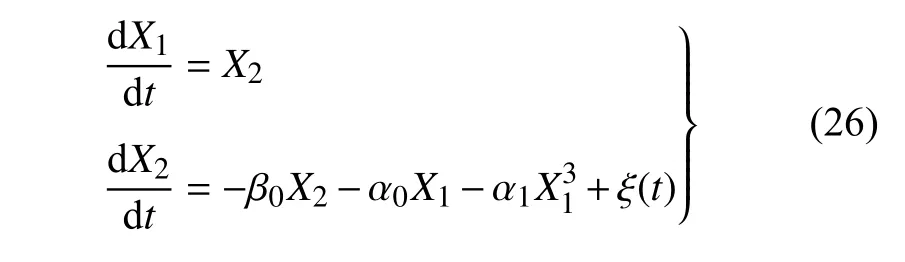
其中,系统参数β0=0.2,α0=-1.5,α1=4.0,ξ(t) 表示均值为零、脉冲幅值为高斯分布的泊松白噪声,且脉冲平均达到率λ=5,方差E[Y2]=0.1.

首先,在状态空间中选择一个中心域ΩG=[-2,2]×[-4,4],将其均匀划分为50×50的网格,取网格节点作为二元高斯基函数的中心(均值),则激活函数个数NG=nc×nc=50×50,并选取中心域网格尺寸作为二元高斯基函数的标准差,即σj=(0.08,0.16).相应地,选取比中心域稍大的样本域为ΩS=[-3,3]×[-6,6],样本点个数NS=ns×ns=100×100,具体参数选取可参见文献[27-28,30],时间步长为Δτ=0.01 s.考虑到高阶偏导数项对广义FPK 方程的贡献很小,此处仅保留前6 阶偏导数项.

系统(26) 的初始条件为当t=0时,在(x1,x2)=(0,0) 处的概率为1 的Delta 函数.可通过对动力学方程(1) 短时近似,获得转移概率密度函数,结合路径积分法,得到时刻t=Δτ的概率密度函数p(1),再由径向基神经网络拟合p(1),相应的权值系数向量设为c(1).在此基础上,可利用递推公式(25) 得到后续任意时刻的概率密度函数.

图2 给出了t=2,2.5,3,6 s 时刻分别由径向基神经网络方法和蒙特卡罗模拟得到的边缘概率密度函数结果.从图2 可以看出,系统(26) 响应在2～6 s这一过程中,位移概率密度函数呈双峰,而速度概率密度函数为单峰.并且,位移概率密度函数的双峰现象逐渐有所抑制,但仍维持双峰状态,意味着在泊松白噪声激励下系统(26) 易发生小偏移.径向基神经网络解的均方根误差分别为3.895×10-3,2.714×10-3,1.815×10-3与1.246×10-3.由图2 也可知径向基神经网络结果与蒙特卡罗模拟结果高度吻合.此外,径向基神经网络算法所运行的总时间仅为54.65 s,远远小于蒙特卡罗模拟所需时间2.5 h.

图2 不同时刻系统(26) 的边缘概率密度函数(实线:径向基神经网络解,符号:蒙特卡罗模拟结果)Fig.2 Marginal PDFs of system(26) at different time(lines:RBF-NN solutions,symbols:MCS results)

图3(a)和图3(b)分别给出了本文算法所获得的位移概率密度函数演化曲面与等值曲线图,从中可以看出该系统响应的演化规律.另外,从图3 也可以看出,当t=6 s 时,系统(26) 的响应接近于稳态,此时系统的联合概率密度函数如图4(a)和图4(b)所示,概率密度函数呈现较为陡峭的双峰现象,但即便如此,径向基神经网络仍能近乎完美地捕捉其响应的强非线性特征.

图3 系统(26) 的位移概率密度函数演化Fig.3 The displacement PDF evolution of system(26)

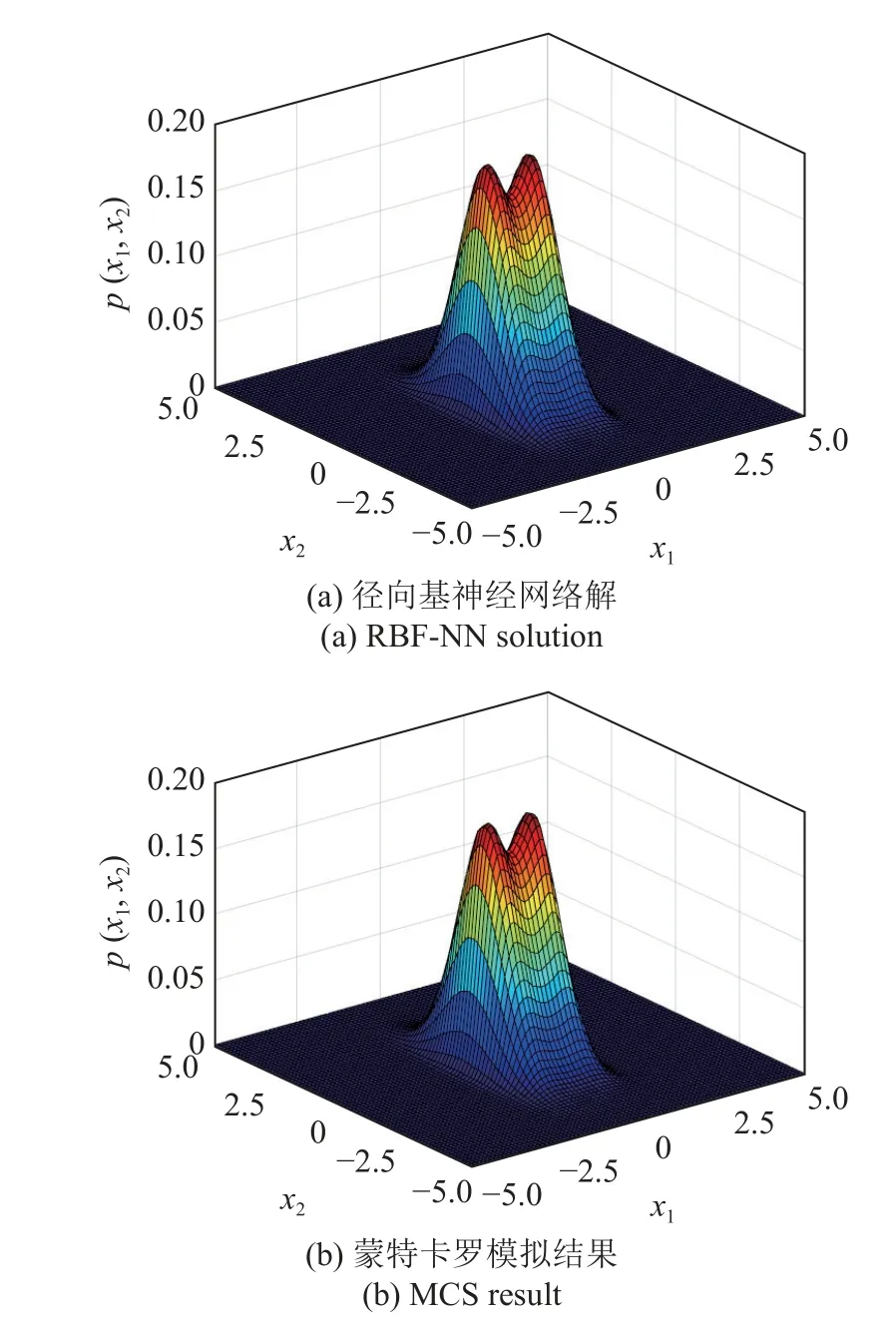
图4 当t=6 s 时系统(26) 的联合概率密度函数Fig.4 The joint PDF of system(26) at t=6 s

为了进一步了解所提出的算法,在此探究不同中心域网格数的划分对计算结果的影响.保持兴趣域大小不变,选取中心域网格尺寸作为二元高斯函数的标准差,且NG=nc×nc.根据算法,所获得的各时刻概率密度函数相对于蒙特卡罗模拟结果的均方根误差及计算时间如图5 所示,在一定的范围内提高网格点数,精度会有一定的提高,但是增加到一定程度后,精度提高并不明显.然而,过多的网格点数会导致计算量大大增加.

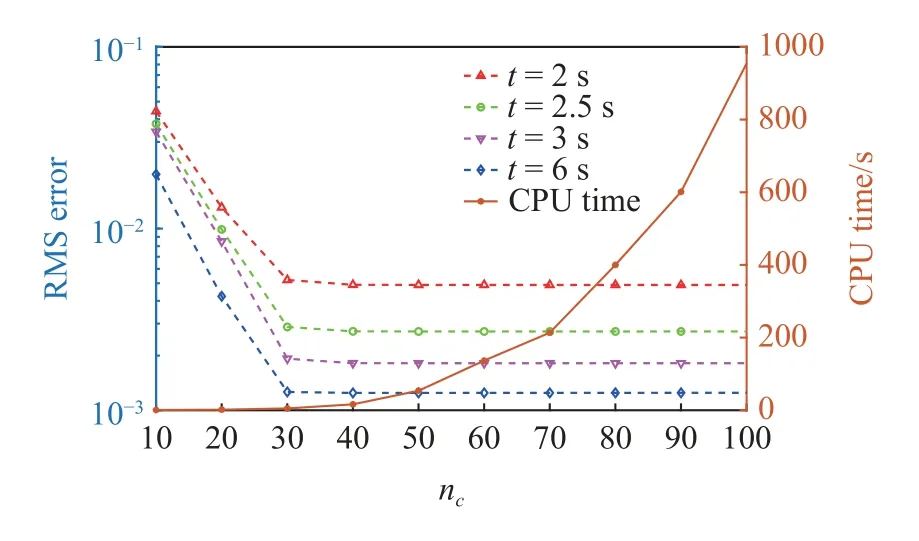
图5 不同中心域网格数对算法的均方根误差与计算时间的影响Fig.5 The effect of different number of meshes in the central domain on the root mean square(RMS) error and CPU time of the algorithm

2.2 三稳态Van der Pol-Duffing 系统

考察一个在泊松白噪声激励下的三稳态Van der Pol-Duffing 系统[32],其在状态空间中的运动方程形式如下

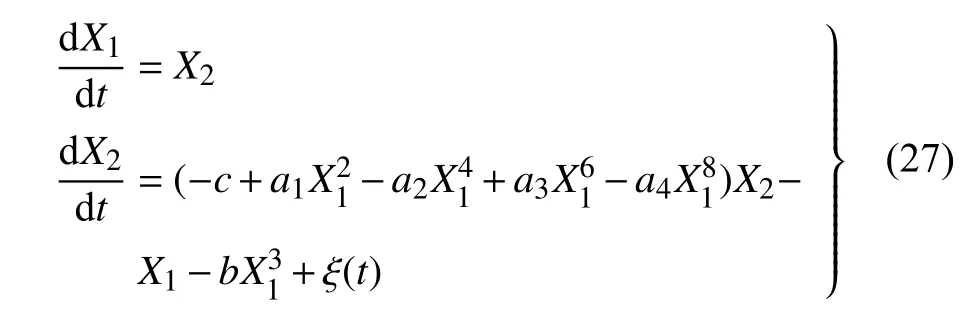
其中,系统参数设置为:c=0.116,a1=1.51,a2=2.85,a3=1.693,a4=0.312,b=2.0.ξ(t)为零均值泊松白噪声,其脉冲幅值呈高斯分布,且脉冲平均达到率λ=5,方差E[Y2]=0.02.

类似地,在状态空间中选择中心域ΩG=[-2.5,2.5]×[-5,5],将其均匀划分为80×80的网格,取网格节点作为二元高斯函数的中心(均值),即NG=80×80,并采取中心域网格尺寸作为二元高斯基函数的标准差,即σj=(0.062 5,0.125).相应地,样本域ΩS=[-3.75,3.75]×[-7.5,7.5],样本点个数NS=160×160.时间步长为Δτ=0.01 s.同样,广义FPK 方程也截断至第6 阶偏导数项.

利用本文算法,分别计算了系统(27)在t=0.01～80s 时刻的瞬时概率密度函数.部分时刻下的瞬时概率密度函数如图6 所示.当t=10,20,40和80s 时,相应的径向基神经网络解的均方根误差分别为8.730×10-4,3.157×10-4,6.752×10-4和6.816×10-4.由图6 可知,径向基神经网络解与蒙特卡罗模拟数据同样非常吻合,展现了其较强的拟合能力;系统响应概率密度函数随着时间演化,由最先的单峰向逐渐演化为三峰.此外,本算例的蒙特卡罗模拟所需时间远超过6.0h,而径向基神经网络算法计算总时间仅需1900.65 s,具有非常高的计算效率.

图6 不同时刻系统(27) 的边缘概率密度函数(实线:径向基神经网络解,符号:蒙特卡罗模拟结果)Fig.6 Marginal PDFs of system(27) at different time(lines:RBF-NN solutions,symbols:MCS results)

图7(a)和图7(b) 给出了本文方法所获得的位移概率密度函数演化曲面与等值曲线.从图7 可以看出该系统响应的演化规律,位移的概率密度函数由单峰向多峰演化,并呈向两边扩散的趋势,且当t=80s 时,系统(27) 的响应接近于稳态,此时系统响应的联合概率密度函数如图8 所示,呈复杂的“外筒内锥”形,响应的非线性特征明显且较为复杂.对比可知,径向基神经网络解与蒙特卡罗模拟结果相当一致,所提方法在处理此类复杂非线性问题时也能达到较好的拟合效果.

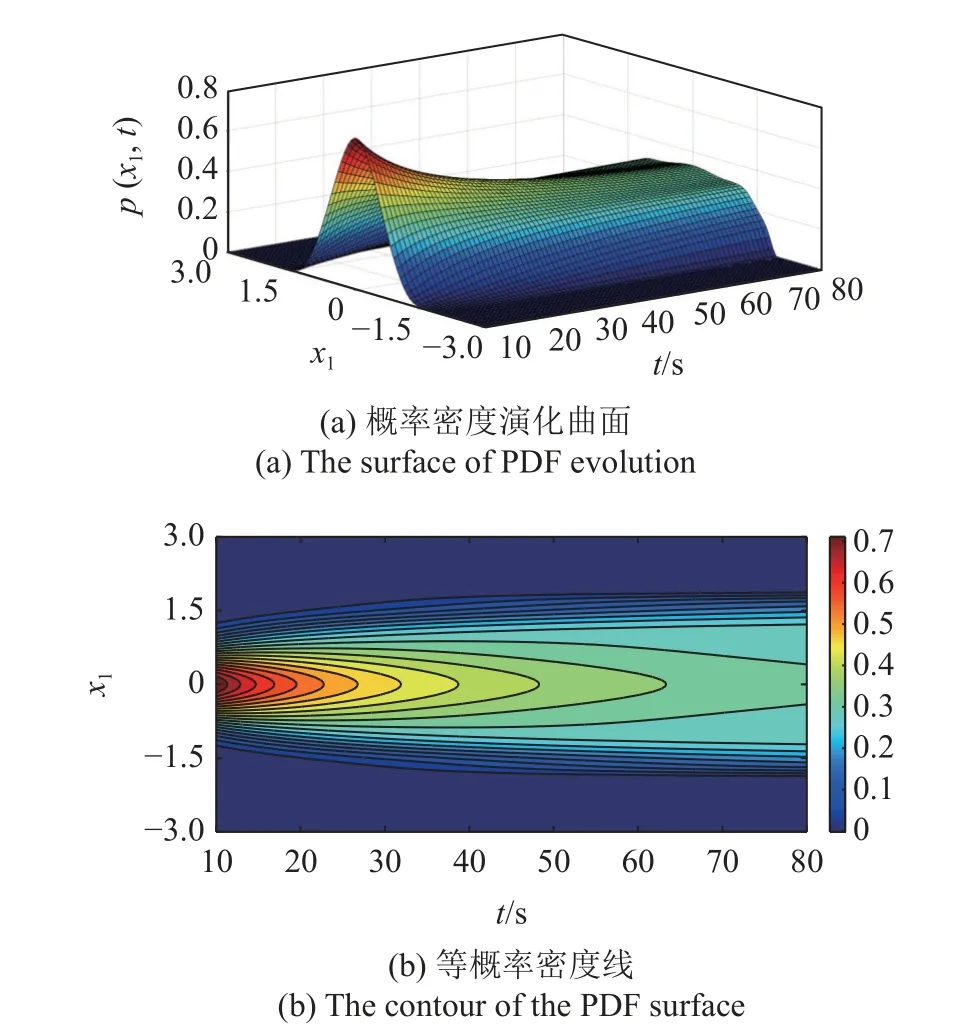
图7 系统(27) 的位移概率密度函数演化Fig.7 The displacement PDF evolution of system(27)

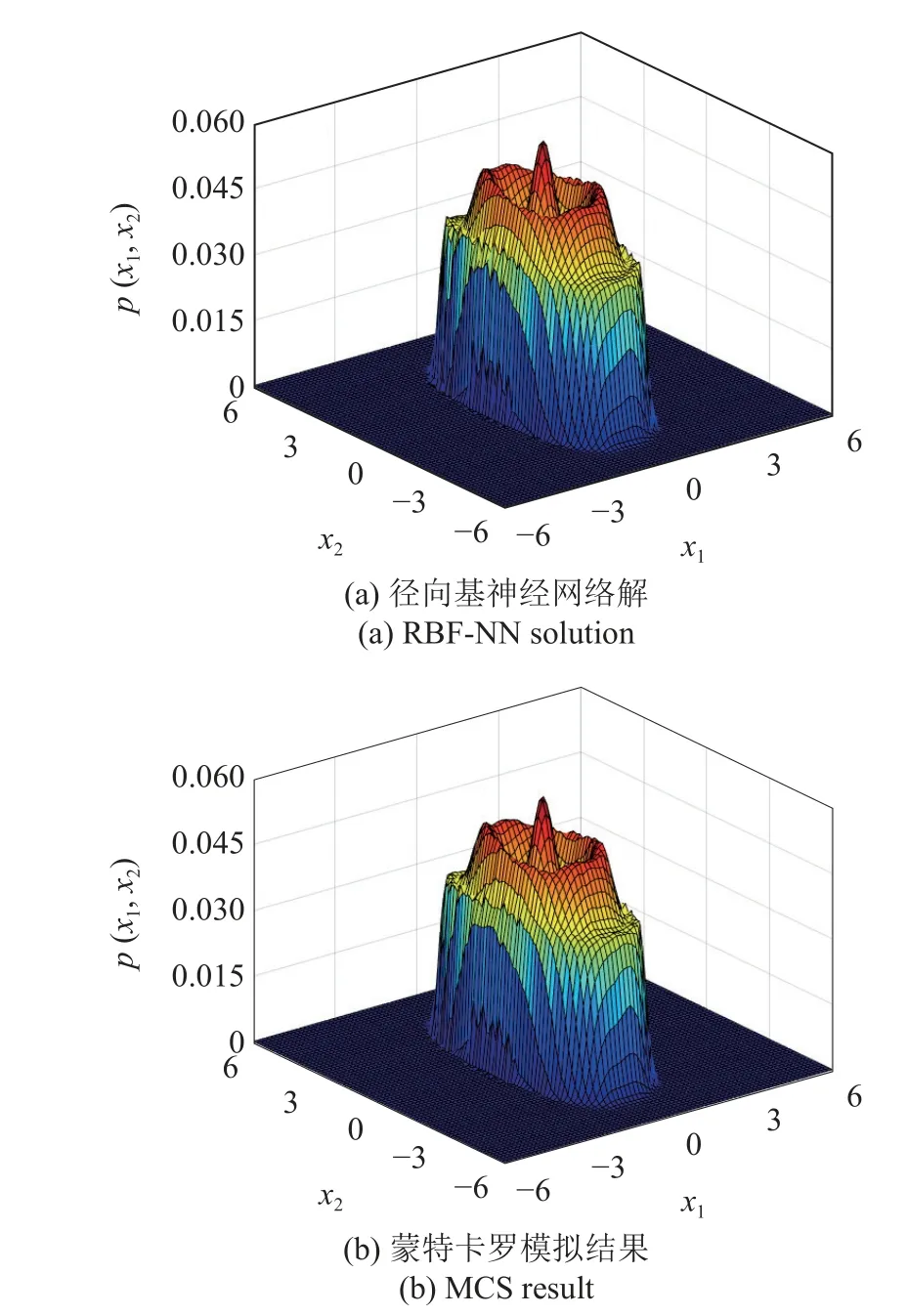
图8 当t=80s 时系统(27) 的联合概率密度函数Fig.8 The joint PDF of system(27) at t=80s

3 结论

综上所述,本文所提出的径向基神经网络半解析方法应用于单自由度强非线性系统在泊松白噪声激励下的瞬态响应分析是切之有效且具有广阔前景的.两个不同的强非线性系统实例证明了该方法的适用性.该方法获得的半解析瞬态解与相应的蒙特卡罗模拟数据相比展现了相当高的精度,兼具较高的计算效率.系统瞬态响应的复杂非线性特征能够被很好地捕捉,从而准确预测泊松白噪声激励下非线性系统响应的时间演化规律,为结构动力反应分析与可靠度设计提供重要依据.更重要的是,不同以往分析方法所获得的数值解,本文方法所获得的高精度瞬态解为半解析形式,不仅可作为基准解检验其他非线性随机振动理论方法的精度,而且对结构的优化设计同样存在重要的应用价值.当然,所提方法仍存在一定的局限性,在推广高维解法时难免受“维数灾”的影响,使得数据矩阵高度密集.为此,进一步结合降维方法,或相关数据点的优化算法诸如稀疏矩阵、遗传算法等是十分必要的.