波场梯度法研究进展

曹飞煌，梁春涛*

1 地球勘探与信息技术教育部重点实验室（成都理工大学），成都 610059

2 地质灾害防治与地质环境保护国家重点实验室（成都理工大学），成都 610059

0 引言

十九世纪以来，利用地震波的振幅和相位信息可以获得地球内部的相关结构特征，传统方法通常集中于分析单台、双台或多台的相位或走时信息.波场梯度法更广泛地考虑了波场的空间变化信息，可以提取更多的波传播特性，比如相速度、几何扩散、辐射花样、方位角变化、衰减、应力、应变和旋度等等.而这些属性的变化可以进一步用于地震波走时拾取（Sollberger et al.,2016）、场地效应分析（Langston et al.,2009）和地球内部结构成像（Liang and Langston,2009）.该方法可用于多种震相或震源的波场梯度分析，比如体波（Langston et al.,2006;Langston,2007a）、面 波（Cao et al.,2020;Liang and Langston,2009;Porter et al.,2016;周鲁等,2017）和环境噪声（Cao et al.,2019;de Ridder and Curtis,2017）等.

波场梯度法自Langston 等在2007 年提出至今已十余载，基于这一基本原理的地震反演技术得到较好发展.Langston 在2007 年同年发表的三篇论文给出了时间域、频率域、线性台阵和二维台阵的波场梯度法（Langston,2007a,2007b,2007c），标志着波场梯度法这一成像技术基本原理的建立.Langston 和 Liang（2008）提出了圆柱坐标系下的波场梯度方法；由于地理空间的约束，大多台阵并非均匀分布，不规则台阵的波形空间梯度分析在一定程度上增加了截断误差，而基于台阵空间几何分布的加权反演为波场梯度法在不规则台网上的应用提供了技术支持（Liang and Langston,2009）.基于该方法，周鲁等（2017）计算了三分量波场梯度法；Maeda 等（2016）将波形空间梯度计算过程中参考点设置为没有波形记录的网格点，然后将其应用于Hi-net 台网，重构了网格点上的地震波场，显示了非均匀介质对地震波传播路径影响的特点；周鲁（2018）使用同样的方法获得了USArray 重构的地震 波 场.Cao 等（2020）将Liang 和Langston（2009）提出的加权反演波场梯度分析方法应用于ChinArray，获得了基于方位角变化的地震波传播参数，将这些参数拟合到瑞利面波的方位各向异性模型获得了瑞利面波的方位各向异性，结果与S 波分裂有较好的一致性，瑞利面波的方位各向异性与区域造山带和断层走向也有较好的一致性.相对于传统环境噪声成像，波场梯度法可以直接获得台站（参考位置）下方的频散曲线，同样密度的地震台网可以获得相对较深的S 波速度结构.常英娜等（2022）通过赫尔曼的线性反演程序将波场梯度法计算的瑞利面波的相速度反演到深度上的S 波速度，得到的安宁河—则木河断裂带下方的三维S 波速度结构，显示了安宁河—则木河断裂带及周边地区在上地壳的速度结构分布特征与该区域地质构造相一致.相对于环境噪声成像，同样密度的地震台网可以获得相对较深的S 波速度结构（常英娜等，2022）.

除上所述，基于小波变换（Poppeliers,2010,2011）和三次样条插值的波场梯度分析也得到了发展；Liu 和Holt（2015）提供了波场梯度的赫姆霍兹方程解；Poppeliers 等（2013）将波场梯度法拓展到三维空间台阵，可以得到更准确的地震波传播参数；de Ridder 和Curtis（2017）提出了一种基于波形空间梯度的环境噪声成像，证明了利用波场梯度分析环境地震噪声中存在的Scholte 波的随机波场也可以得到合理的面波相速度和方位各向异性，与传统的环境噪声成像相比，该方法不需要进行环境噪声的互相关，但要求台阵分布较为规则.

1 波场梯度法基本原理与反演技术

在波场梯度法中，第一步是求地震波场的空间梯度，第二步是通过波场梯度系数将波场空间梯度与地震波的相速度、几何扩散、辐射花样和传播方向联系起来，第三步是将地震波传播参数与介质属性相关联.

在波场梯度法求地震波传播参数的过程中，一维台网由于缺乏另一空间维度的信息，仅获得相速度和几何扩散，无法约束方位角相关的地震波传播属性（Langston,2007a）.而二维台网的波形空间梯度法对另一纬度的波场空间梯度也进行了分析，地震波传播在方位角上的变化得到了约束，与一维台网的波场梯度法相比，二维台网的波形空间梯度法额外获得了地震波传播方向的变化和地震波振幅随方位角变化的参数（Langston,2007b）.

1.1 一维台网的波场梯度法

通过胡克定律可知，位移梯度（波场梯度）比位移本身与介质的力学属性关系更为密切，这种关系可以从波动方程得到解释.在纯弹性介质中，一维波动方程可以表示为（Langston,2007a）：

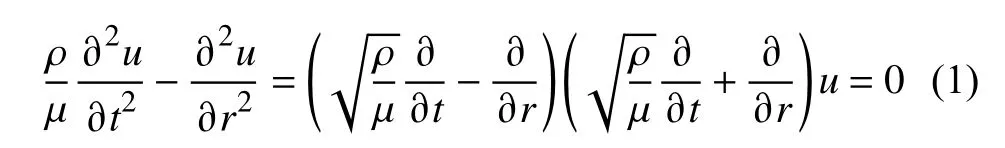
在波场梯度法中,主要利用参考位置附近台站间的波形差异来测量参考点波形的空间梯度，波场空间梯度与地震波传播特征可以通过两个分别与振幅变化和相位变化相关的波场梯度系数A和B联系起来.假设子台网（由参考点与附近台站组成，图1）范围内介质的横向物理性质差异较小，振幅的空间变化函数G和相位随时间和空间变化的函数f便可以更广泛地描述波（体波或面波）的传播特征.在极坐标系下的波动方程表示为（Langston,2007a）：

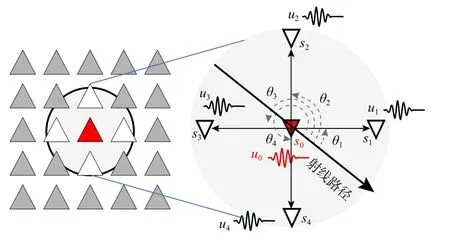
图1 密集台阵子台网示意图，以台站为波场空间梯度计算的参考点.灰色影区内的三角形表示子台网，其中红色三角表示参考台站 S0(r0,θ0)，白色三角为辅助台站S i(ri,θi),i=1,2...；子台网对应的波形为ui(i=0,1,2,..)（修改自Langston and Liang,2008）Fig.1 Subarray diagram using stations as reference location for wave gradient analysis.Triangles represent seismic stations and triangles in gray areas are stations of subarray;red and white stations represent reference station[S0 (r0,θ0)] and supporting stations,respectively (modified from Langston and Liang,2008)

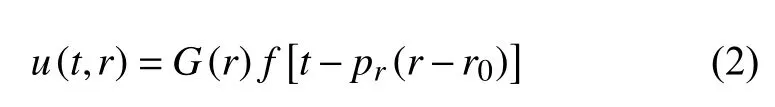
式（2）中pr代表径向（r）方向的慢度，r0为参考位置.对公式（2）求导得：

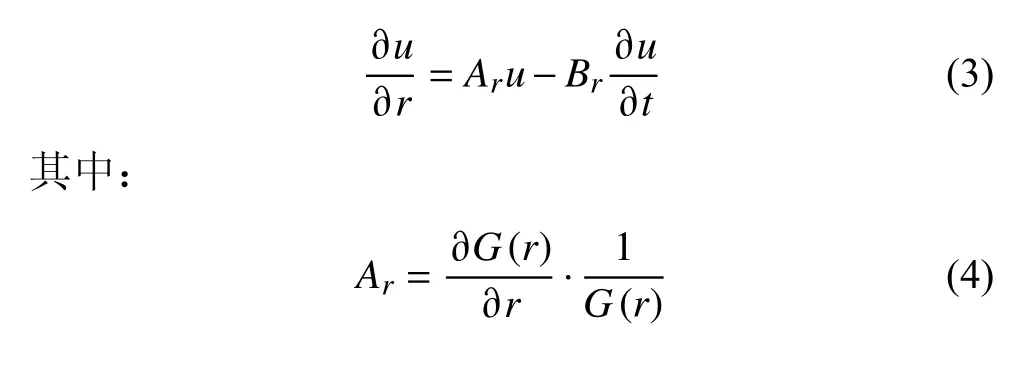
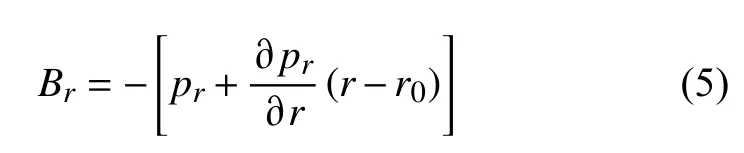
其中Ar表示归一化的波场振幅的空间梯度，Br表示介质慢度沿射线方向的变化.系数Ar在路径r0→r上的积分可得振幅随距离的变化，即几何扩散：

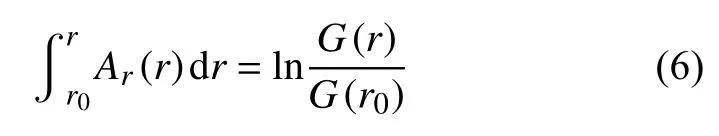
系数Br在路径r0→r上的积分可得水平慢度：

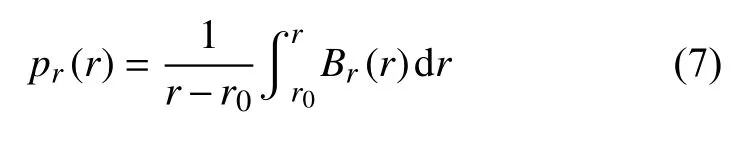
1.2 二维台网的波场梯度法

在二维台网中，波动方程表示为（Langston,2007b）：

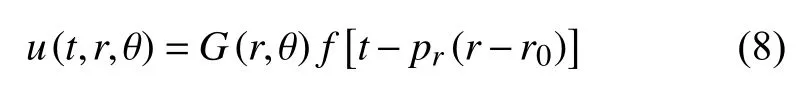
对公式（8）对θ 求偏导：

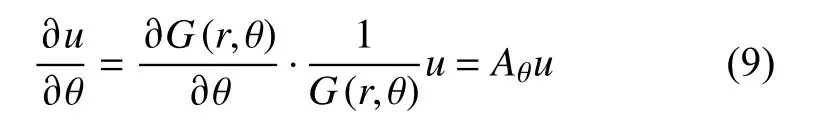
系数Aθ在方位角 θ0→θ上积分可以得到振幅随方位角的变化，即辐射花样：

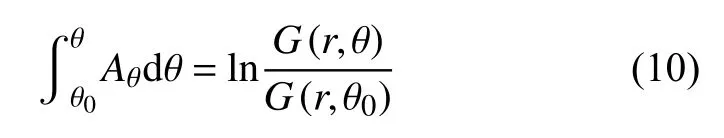
将波形的空间梯度转换到笛卡尔坐标系，式（8）写为：

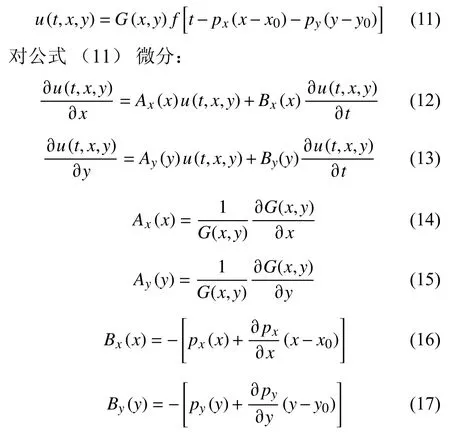
根据极坐标系与二维笛卡尔坐标系的转换关系（x=rsinθ;y=rcosθ），波形的空间梯度在这两种坐标系下的关系为：

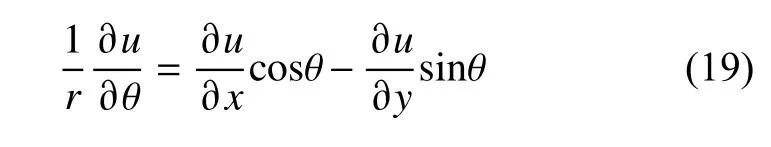
联合公式（4）、（12）-（15）和（18）得到笛卡尔坐标系下的几何扩散：

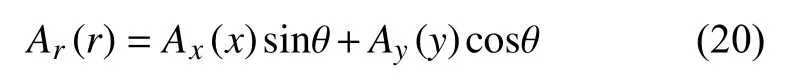
联合公式（10）、（12）-（15）和（19）得：

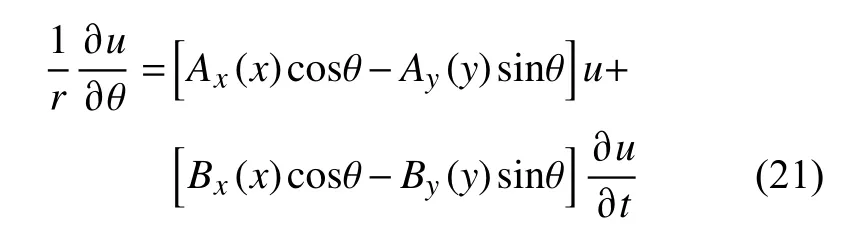
联合公式（19）和（21）得：

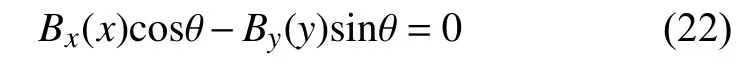
根据公式（22）得到地震波在台站的水平入射方位角：

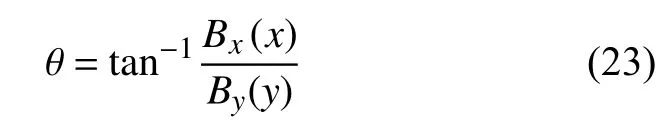
联合公式（8）、（18）和（19）得笛卡尔坐标系下的辐射花样：

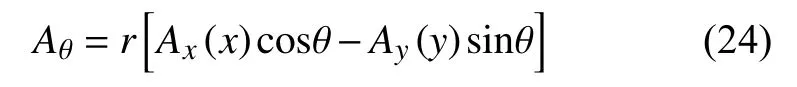
笛卡尔坐标系下对应的慢度为：

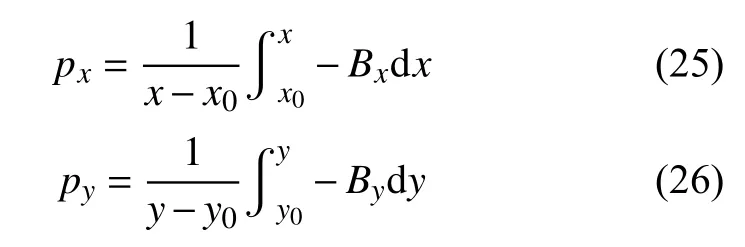
假设子台网范围内的介质在物理性质上差异很小，或(x,y)→(x0,y0)时 ：

根据空间几何关系，径向方向慢度为：

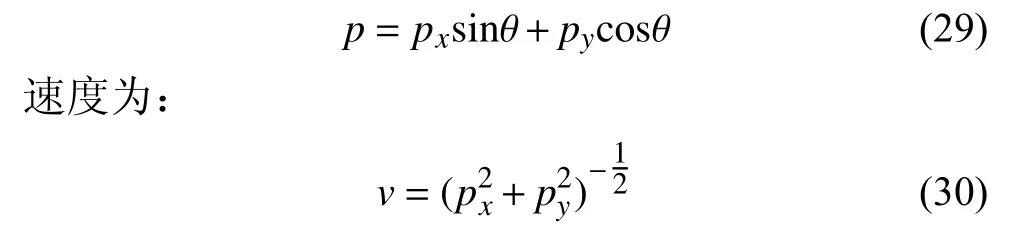
根据公式（20）、（24）和（25）,方位角与慢度的关系为：

1.3 反演方法

从相速度v、地震波传播方向(θ,ϕ)、几何扩散Ar、辐射花样Aθ、波形空间梯度和波场梯度系数A、B的关系可知，只要获得A和B，就可以直接获得地震波的传播参数的解析解，只要获得波形的空间导数和时间导数（粒子运动速度），就可以直接获得系数A和B，而波形的空间导数和时间导数可以从地震台网记录地震波场ui(i=1,2...N) 计算得到.因此，在波场梯度法反演过程中，首先从ui(i=1,2...N)反演波形的空间梯度，然后利用空间梯度计算波场梯度系数Ai和Bi(i=x,y)，最后将Ai和Bi(i=x,y)代入波形空间梯度系数A、B和地震波传播参数的关系式得到地震波的传播特征.

1.3.1 波形空间梯度反演

波形的空间梯度计算方法根据台网的空间几何分布（规则分布和不规则分布）、滤波方法（比如傅里叶变换和小波变换）或反演技术（有限差分法、三次样条插值、加权反演）的不同而有所差异.对于规则分布的台网可以直接利用有限差分法（Langston,2007a,2007b,2007c）或三次样条插值方法（Liu and Holt,2015），而对于不规则分布的台网可以利用加权反演方法（Liang and Langston,2009）.

以二维台网为例，当选定某个台站为参考点时（图1），子台网内的波形空间差异用泰勒展开式可以表示为：

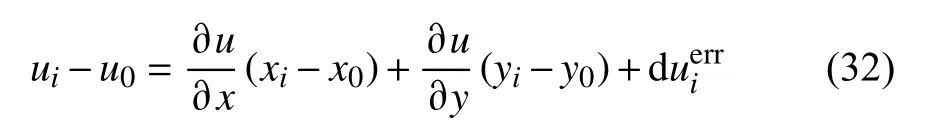
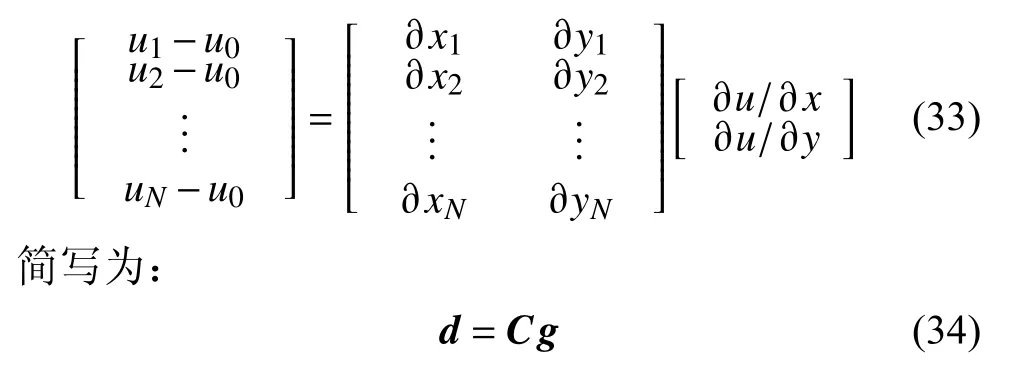
公式（33）中，∂u/∂x和∂u/∂y是未知量，ui、u0、∂xi和∂yi（i=1,2,…,N）都为已知量，因此只要辅助台站Si的数量大于或等于2，利用公式（33）就可以直接解出波形的空间梯度.

以网格点为参考点时（图2），子台网内的台站i的波形ui可以表示为：

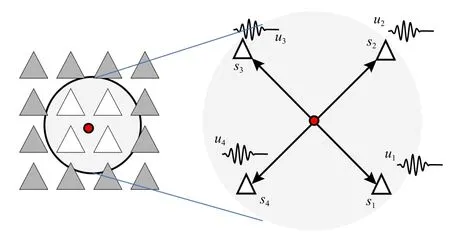
图2 二维规则台阵子台网示意图，以网格点为波形空间梯度计算的参考点.红色圆为网格点，白色三角形为辅助台站Fig.2 Subarray diagram in a 2-D regular seismic array,where the grid point (i.e.,red dot) is the reference location for wave gradient analysis and white triangles represent supporting stations

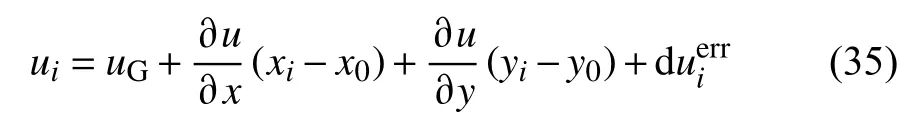
其中uG为参考网格节点的波形.公式（35）用矩阵的形式表示为：

公式（36）中，∂u/∂x、∂u/∂y和uG是未知量，ui、∂xi和∂yi（i=1,2,…,N）都为已知量，因此只要辅助台站Si的数量大于或等于3，基于公式（33）就可以直接解出波形的空间梯度和网格点的波形（Maeda et al.,2016）.

在二维不规则台网中（图3），单纯利用有限差分计算的波形空间梯度使得公式（32）的截断误差增大（Langston,2007b），通过空间几何的加权可以有效地压制由于台阵空间分布导致的误差增大效应（Liang and Langston,2009）.首先根据辅助台站相对于参考台站（或网格点）的位置给定不同的权重（Liang and Langston,2009）：

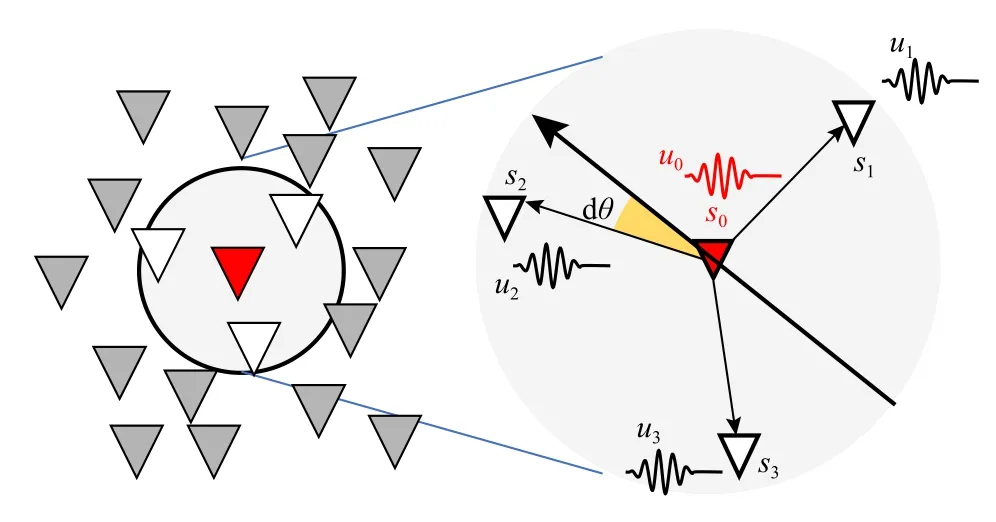
图3 二维不规则台阵中的子台网，以台站为波形空间梯度计算的参考点（修改自Liang and Langston,2009）Fig.3 Subarray diagram in a 2-D regular seismic array,where the red station is the reference location for wave gradient analysis and black triangles represent supporting stations (modified from Liang and Langston,2009)

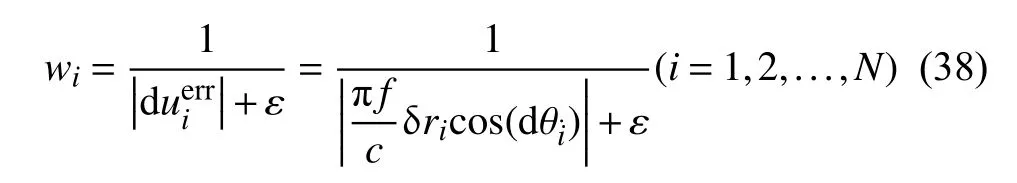
其中wi为权重系数，f为中心频率，c为相速度，δri为辅助台站到参考台站的距离，dθi为震源到参考位置的射线路径与辅助台站到参考位置射线路径之间的夹角，ε表示波形数据质量相关的误差，数据质量差ε 值大.将权重系数矩阵：

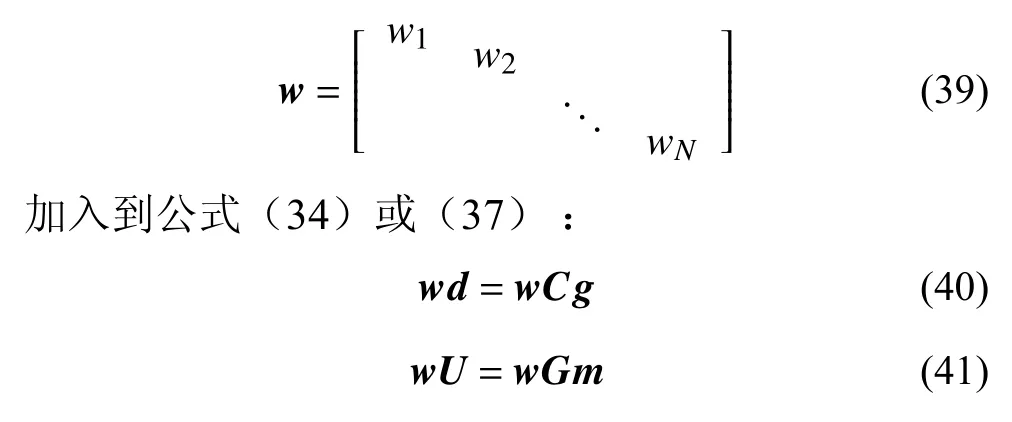
反演公式（40）或（41）便可获得不规则台网的波形空间梯度.

1.3.2 波场梯度系数A、B的求解

以二维台网为例，公式（12）和（13）显示，波形的空间梯度和时导数是求解波形空间梯度系数的前提.利用2.4 节的方法可以获得波形的空间梯度，而波形的时间梯度可以从地震波的时间序列获得，前人研究表明，利用波形的时空变化求解系数A和B有很多途径，比如傅里叶变换（Langston,2007a）、小波变换（Poppeliers,2010）、时间域的希尔伯特变换（Langston,2007c）和离散时间矩阵反演（Langston,2007a）.以时间域为例，假设在时窗M(t1:tM) 内不同时间样点A（或B）的差异很小，公式（12）和（13）在离散时间样点上表示为（Langston,2007a;Maeda et al.,2016）：

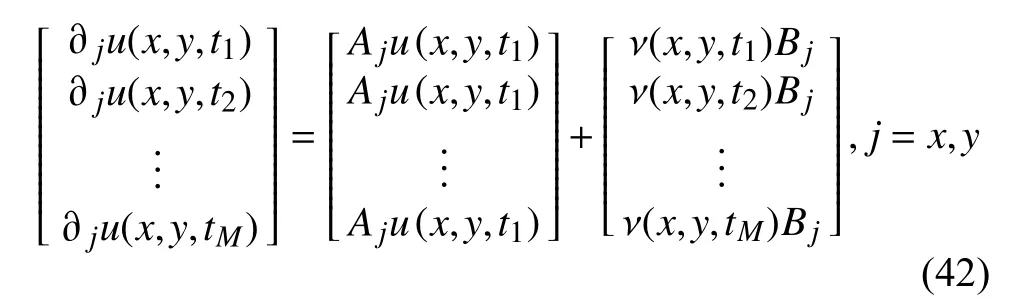
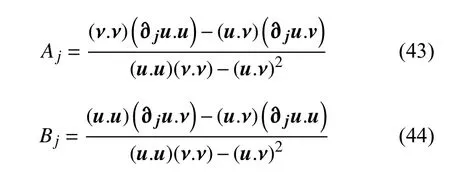
其中ν，∂ju和u分别表示质点速度、质点位移u(x,y,t)的空间导数∂u/∂j离散时间样点上的矩阵.

另一种更精确的方法是对公式（12）和（13）进行希尔伯特变换，构建解析信号，然后求解每个时间样点上系数A和B的解析解，Langston（2007c）给出了波场、波场梯度和波场时间导数与系数A、B的关系式.

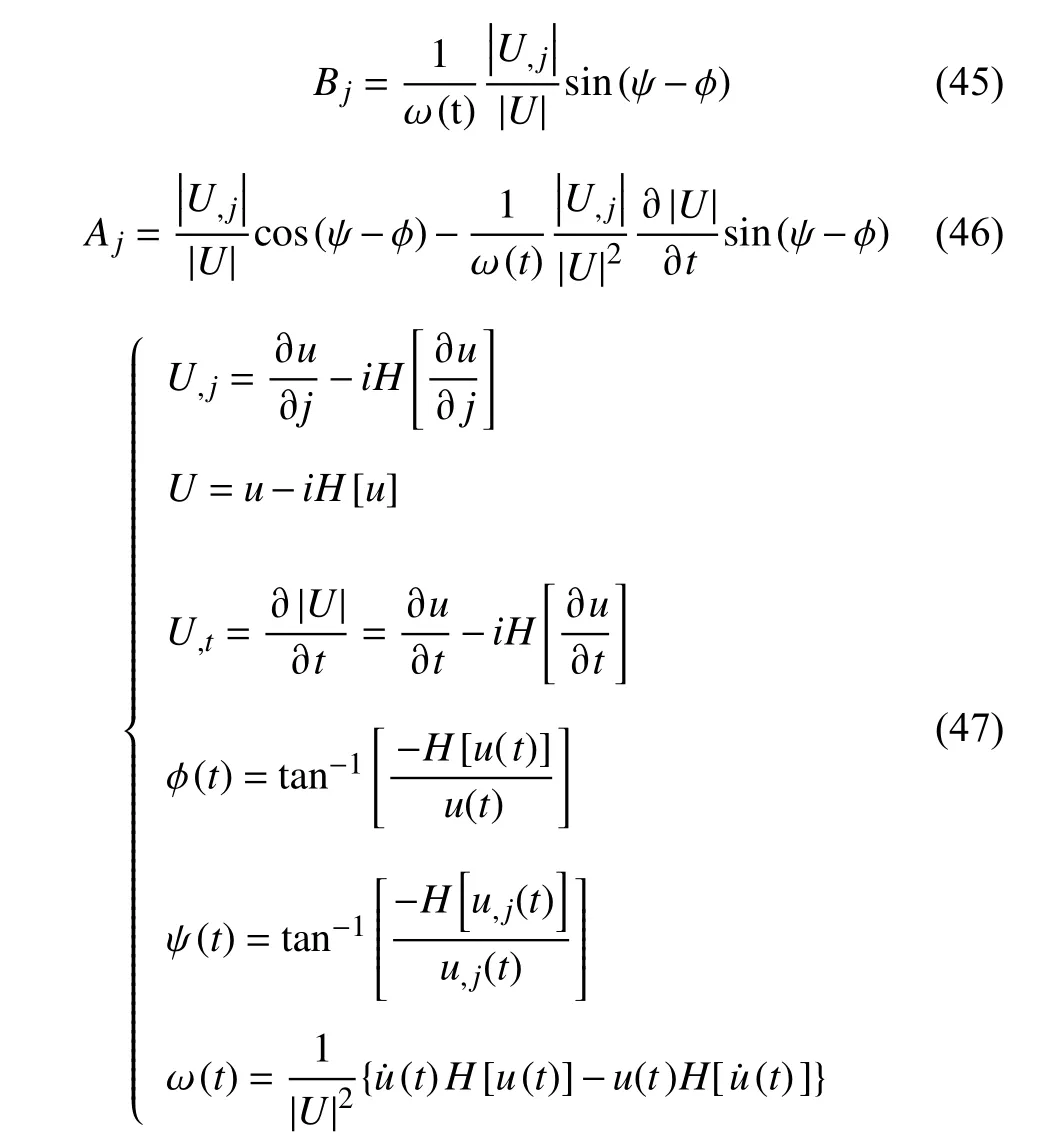
其中H[ ]为希尔伯特变换，分别表示波场空间梯度和波场的包络函数或瞬时振幅，ψ 和 ϕ分别表示波场空间梯度解析信号和波场解析信号的瞬时相位，(t)为波场的时间导数.将公式（45）和（46）获得的波场梯度系数代入公式（20）、（23）、（24）、（27）和（28）便可以获得地震波传播的几何扩散、方位角、辐射花样和慢度.

1.4 误差和精度

波场梯度法在设置子台网的过程中需要综合考虑辅助台站的数量、成像误差和成像精度之间的关系.根据公式（33）和（36），基于不同的参考位置类型，子台网至少需要2～3 个辅助台站，而在实际应用中，更多的辅助台站（≥5）可以一定程度上增加稳定性.波场梯度法的成像分辨率与子台网大小相关，波场梯度法的一个基本假设是子台网范围内的介质在物理性质上是常数（Langston,2007a），因此较大的子台网尺度对小尺度异常体的分辨能力减小.

另一方面，波场梯度法的成像误差和分辨率与台间距呈负相关，台间距较大的台网对高频面波成像产生较大的截断误差（Langston,2007a;Liang and Langston,2009）.Langston（2007a）的理论推导表明，通过有限差分法获得的波场空间梯度要满足截断误差小于10%，需要台间距小于12%的波长.由于震中距的差异，不同位置台站间的相位存在一定的时移，这种时移会增大波场空间梯度反演过程中的高阶截断误差（Langston,2007a），该误差不仅与子台网间的空间几何分布（ri,dθi）相关，也与中心频率f和相速度c相关（Liang and Langston,2009）.因此，通过人为增加相速度（折合速度法）和加权反演（公式41）可以很大程度上降低时移和不规则台网对截断误差的影响（Langston,2007a;Liang and Langston,2009）.常英娜等（2022）的理论测试部分表明，在8%的噪声水平下波场梯度法可以基本恢复与台站间距尺度相当的速度异常；实际应用表明，通过加权反演联合折合速度法获得的波场空间梯度也适用于接近一个波长的台间距的密集台阵（Porter et al.,2016）.只要台站足够密集，水平或垂直线性台阵（Langston,2007a;Langston and Ayele,2016）、二维规则或不规则台阵或带状台阵（Langston,2007b;Liang and Langston,2009）都适用于波场梯度法.与其他成像方法相同，较大的平滑因子会降低成像的误差和削弱成像分辨率.

2 波场梯度法的应用

随着密集台阵不断发展，波场梯度法在地球动力学方面得到了很好的应用，比如复杂介质地震响应研究、波场重构、地震成像（油田、测井、断裂带、壳幔结构或月壳）等.Langston（2007b）、Langston 和Liang（2008）、Poppeliers（2010）利用波场梯度法分析了新马德里台阵记录的2.8 级地震、南加州地震台网（ANZA）记录的2007 年M8.1 所罗门地震和台湾省竹水河谷爆炸源和格伦多拉回填矿坑爆炸源的地震波传播属性，获得了不同震源在不同介质条件下不同震相的地震波的水平应变、水平旋度、相速度和传播方向的变化.方位角、慢度、应变和旋度在时间序列上的变化与震相有很好的对应关系（图4、5），利用这种对应关系可以用于震相识别相应的到时拾取（Sollberger et al.,2016）.结合地震波射线传播的假设，Langston和 Ayele（2016）将波场梯度法应用于圣安德烈斯断层测井的垂直阵列，获得了断裂带下方的体波速度模型和衰减结构.

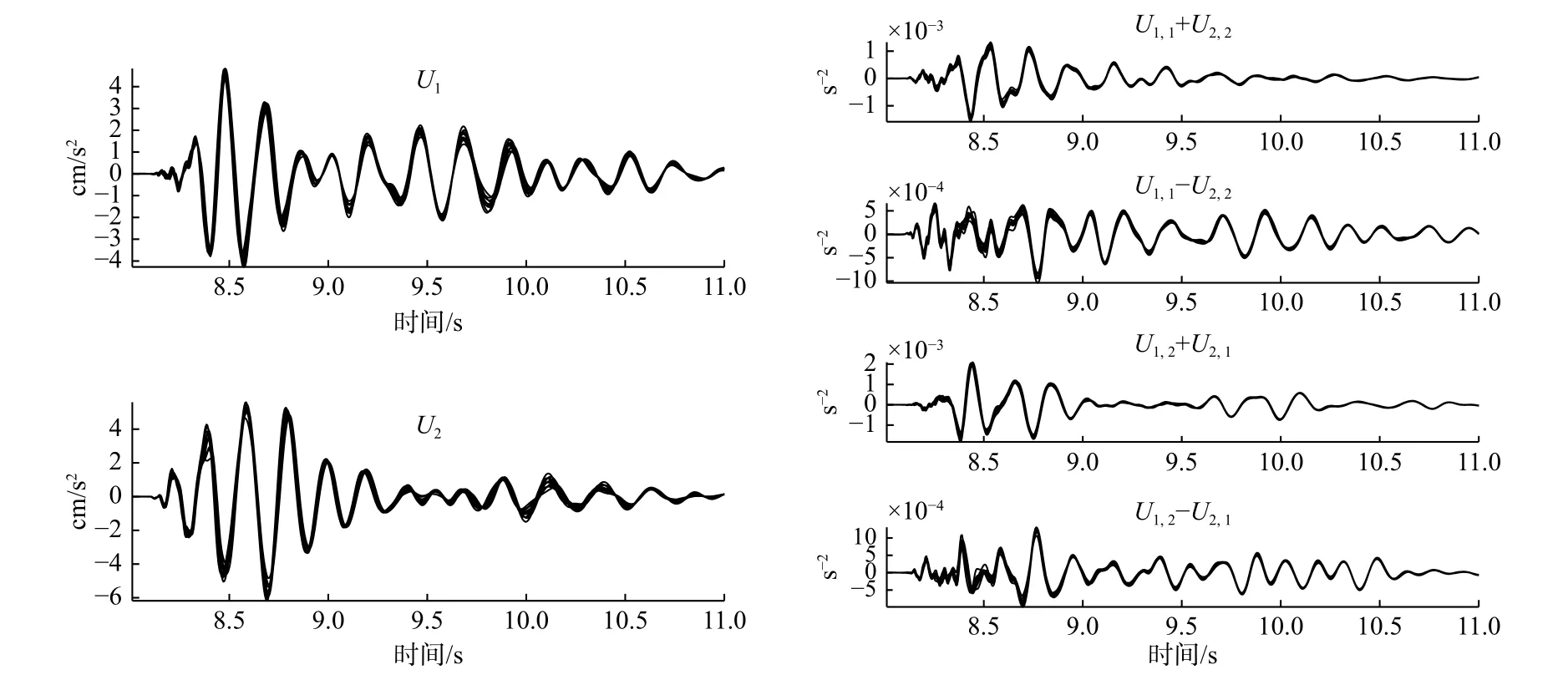
图5 利用TAIGER 记录的爆炸源的水平分量加速度计算的应变和水平旋转.U1 和U2 分别对应于X 和Y 方向的水平加速度.U1,1+U2,2、U1,1-U2,2、U1,2+U2,1 和U1,2-U2,1 分别为面应变、法向应变的微分、两倍的剪切应变和两倍的负水平旋度（引自Langston et al.,2009）Fig.5 Strain and horizontal rotation calculated from the horizontal component acceleration of the explosion source,as recorded by TAIGER.U1 and U2 correspond to the horizontal acceleration in the X and Y directions,respectively.U1,1+U2,2,U1,1-U2,2,U1,2+U2,1 and U1,2-U2,1 are the coordinate-invariant area,normal differential,twice of the shear strains,respectively,in the x-y coordinate system;the negative value is twice the horizontal rotation about the vertical axis (cited from Langston et al.,2009)

Langston（2007a）提出的波场梯度法是一种基于平面波假设的地震数据处理方法，其实波形空间梯度的成像原理不仅适用于能量较强的平面波，同时适用于环境噪声成像.de Ridder 和 Curtis（2017）通过反演Ekofisk 油田密集台阵记录的噪声信号的二阶空间梯度和时间梯度，获得了斯通利波的相速度和方位各向异性.传统的环境噪声成像需要长时间记录的互相关获取面波信号来成像，而基于环境噪声的波场梯度法仅仅需要10 min 甚至更短的记录，便可以计算面波的相速度和方位各向异性，可应用于环境噪声的实时成像，而结合机器学习技术可以进一步地实现3D 速度波形的实时成像（Cao et al.,2019）.

月球浅层地壳被认为是由高度断裂的玄武岩物质组成，其特征是低波速度和极低的固有衰减（Cooper et al.,1974;Latham et al.,1970）.这些物性导致了地震波在月球浅层发生强烈散射，并导致了首波之后出现较为复杂的干涉现象，干扰了后续的S 波、反射波或转换波（Gangi,1972），使得到时难以确定，对利用传统地震成像方法对月球浅层速度结构进行成像造成较大的困难.而波形空间梯度对地震波的旋转能量变化较为敏感，Sollberger 等（2016）利用这种敏感性拾取S 波到时并成功地获取了月球浅层的S 波速度模型和泊松比（图6）.

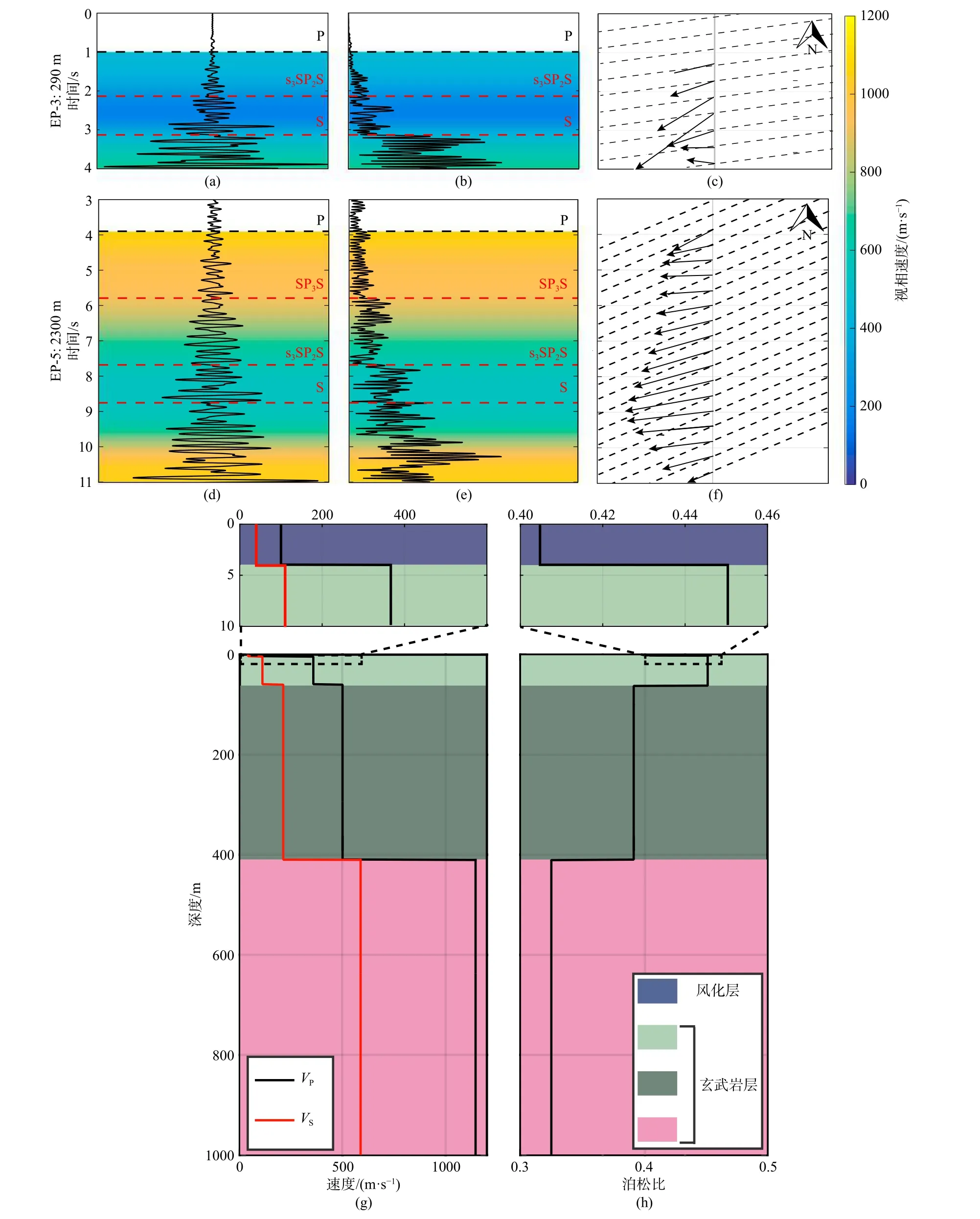
图6 基于波场梯度分析的S 波的视相速度[（a）、（b）、（d）和（e）的彩色底图]、地面转动[（b）和（e）的黑色曲线]、S 波到时[（a）、（b）、（d）和（e）的红色虚线]和传播方向[（c）和（f）的箭头]的结果；图（c）和（g）的虚线表示震源和台阵的连线；（a-c）和（d-f）分别代表震源EP-3 和 EP-5 的结果；图（g）和（h）分别为阿波罗17 号着陆点下方月壳的震波速和泊松比结构（修改自Sollberger et al.,2016）Fig.6 Gradient-based estimates of apparent phase velocity [i.e.,color maps (a),(b),(e),and (f)],rotational ground motion [i.e.,black curves in (b) and (f)],and propagation direction [i.e.,arrows in (c) and (g)].Shear wave arrivals are identified based on their distinct increase in the amount of rotational energy and are marked in red.Dashed lines underlying the propagation direction estimates mark the source-receiver azimuth,according to the survey geometry;(h) shows the seismic velocity and Poisson's ratio structure of the lunar crust below the Apollo 17 landing site (modified from Sollberger et al.,2016)

大型密集台阵的发展使得波场梯度法可以用于研究低频地震信号的波传播属性.目前主要在壳幔地震成像、方位各向异性和波场重构等研究方向得到较好的应用.USArray、ChinArray、Hi-net 分别为美国、中国和日本布设的较为典型的大型密集台阵.Liang 和 Langston（2009）将基于加权反演的波场梯度法应用于USArray，获得了美国西部地区的地震传播参数，其中50～150 s 的瑞利面波高相速度对应于美国西海岸和平原地区，低相速度对应于高原地区.基于Liang 和Langston（2009）相同梯度分析的方法，周鲁等（2017）通过将波形坐标旋转然后进行波场梯度分析，最终获得了美国中东部三分量面波传播变化特征.Liu 和 Holt（2015）将波场梯度系数A和B与Helmholtz 方程关联，获得了经过校正的地震波传播参数，显示了早古生代大陆边缘近似边界的速度变化和火山热点相关的低速异常.为了更好地了解北美大陆的构造演化，Porter等（2016）结合环境噪声互相关和波场梯度法获得了美国大陆的三维S 波速速度模型.该模型中的S波变化突显了造山运动对岩石圈演化的影响.

3 波场梯度法在青藏高原东南缘应用的数据处理流程

川西地区地处青藏高原东南缘，地质构造复杂，是研究青藏高原隆升机制的重要位置（图7a）.基于Cao 等（2020）的研究，接下来我们给出波场梯度法在青藏高原东南缘瑞利面波相速度和方位各向异性研究的一个例子（该例子对应的程序：https://github.com/Feihuang-C/Wave-Gradiometry.git）.

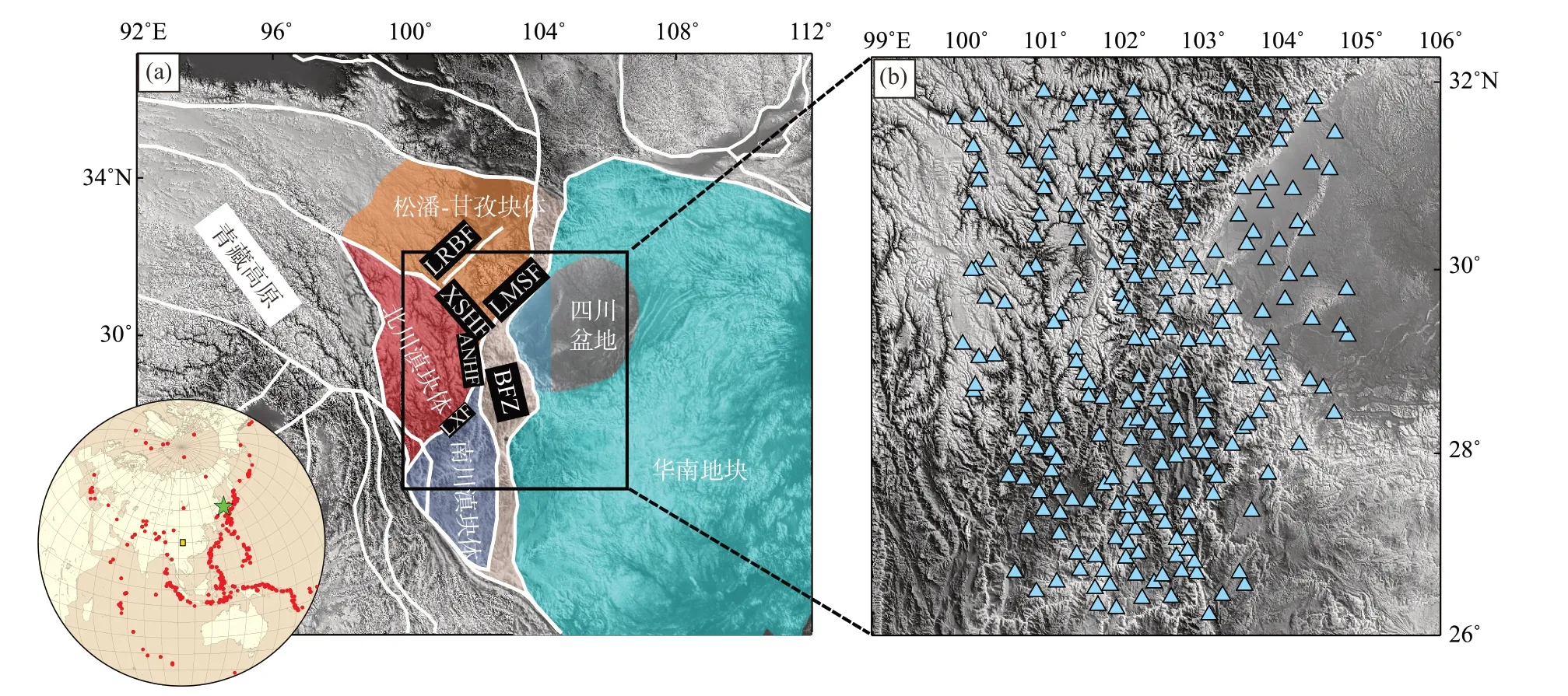
图7 （a）区域构造与（b）台站分布.图（a）中白线是块体边界；左下方的子图为地震事件分布图，红色圆点表示地震，绿色五角星表示鞑靼海峡M6.2 地震，黄色小方块表示研究区域.ANHF：安宁河断层；LMSF：龙门山断裂；XSHF：鲜水河断裂；BFZ：板块边界断裂带；LXF：丽江—小金断裂；LRBF：龙日坝断裂.图（b）中浅蓝色三角形是川西流动台阵（TWSA）（修改自Cao et al.,2020）Fig.7 Geological setting and seismic array.(a) White lines denote the boundaries of tectonic blocks;red dots represent earthquakes;green pentagram indicates the M6.2 earthquake in the Tatar Strait.SGB is the Songpan-Ganzi block;SCB is the South China Block;SCDsB is the south Chuandian subblock;NCDsB is the north Chuandian subblock;ANHF is the Anning He Fault;LMSF is the Longmenshan fault;XSHF is the Xianshuihe fault;BFZ is the boundary fault zone;LXF is the Lijiang-Xiaojin fault.(b) Light blue triangles denote stations of the Temporary West Sichuan Array (modified from Cao et al.,2020)

3.1 数据预处理

（1）选取地震目录：震中距为10°～90°（理论上只要有清晰的面波信号就可以），震级为M5.5～7（图7a）；

（2）截取303 个川西流动台站（图7b）记录的事件波形，去均值，去趋势，去仪器响应；

（3）波形质量控制：面波一致性较好，子台网内面波振幅差异不超过30%（图8b）.

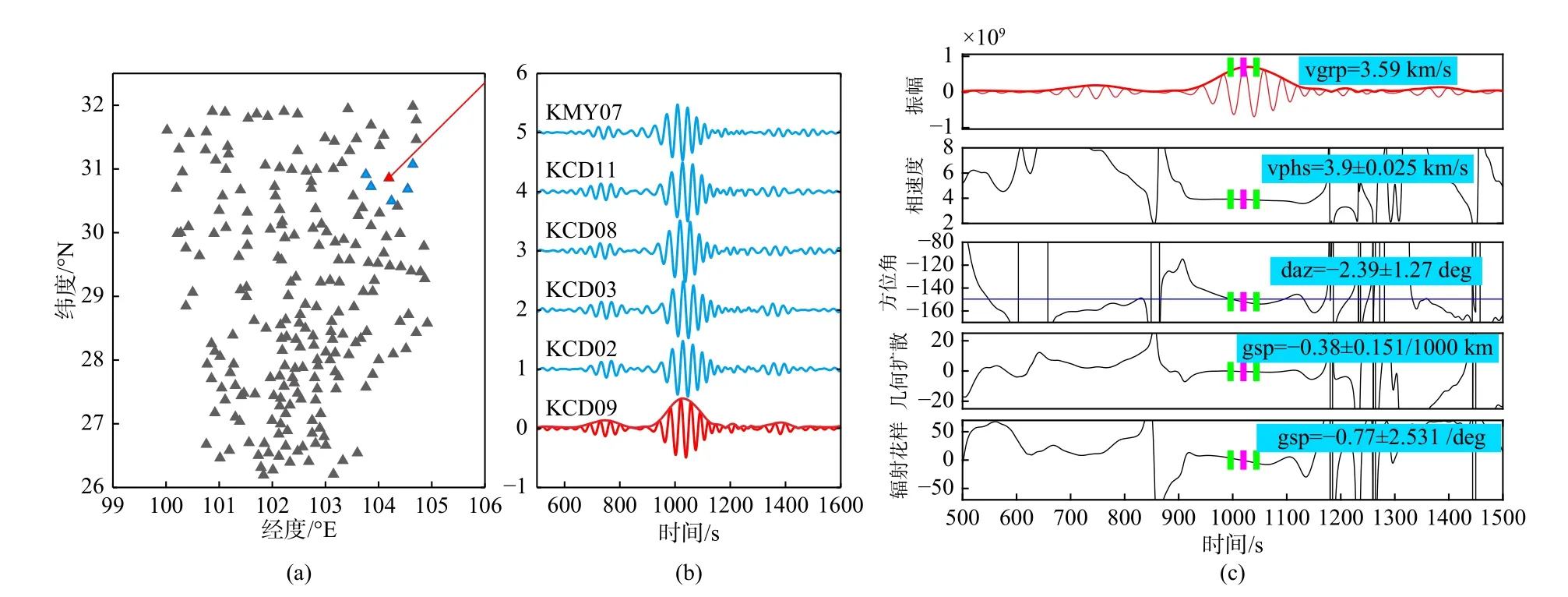
图8 单个参考位置的波场梯度分析结果.（a）子台网空间分布，红色三角形为参考位置的台站，蓝色三角形为辅助台站，红色直线为大圆路径（图7a 绿色五角星）；（b）子台网波形，红色为参考位置台站记录的波形，蓝色为辅助台站的记录的波形；（c）参考位置的波场梯度分析在事件序列上的结果，从上到下依次为参考位置的波形、相速度、方位角变化、几何扩散和辐射花样，蓝色直线标记了大圆路径对应的方位角，紫色短棒标记了瑞利面波最大振幅所在相位的结果，绿色短棒标记了一个周期的时间序列上的结果，该时间序列上的结果用于计算单个地震事件波场梯度分析的标准偏差Fig.8 Wave gradiometry analyses for a single reference location.(a) Triangles represent stations and the red triangle represents the reference location;blue triangles represent supporting stations;the red straight line shows the ray direction (i.e.,green pentacle in Figure 7a);(b) Waveforms of subarray with period of T=40 s;the red trace is the waveform of the reference location,and blue traces are waveforms of supporting stations;(c) Subfigures,from top to bottom,are waveform of the reference location,phase velocity,azimuth,geometrical spreading and radiation pattern,respectively;the blue straight-line marks the great circle azimuth;the vertical bar in the middle marks the timing of the waveform peak;another two green bars are about half of the period apart from the bar in the middle.The standard deviation between these two times is given as errors for corresponding parameters

3.2 波场梯度分析

子台网半径设置为0.5°，以KCD09 台站为参考位置，选定了周围5 个台站为辅助台站，子台网的波形具有较好的一致性（图8b），通过子台网内的波形差异可以获得参考位置的波场空间梯度，利用波场空间梯度进一步获得鞑靼海峡6.2 级地震在参考台站KCD09 的传播参数（图8c）.图8c 显示的是地震波传播参数在500～1 500 s 时窗上的离散时间样点的结果，地震波传播参数在瑞利面波信号段的时窗内具有稳定的结果，而在不同震相相互干涉的时窗内，地震波传播参数出现较大的跃变.拾取瑞利面波最大振幅相位（图8c 紫色短棒）所在时刻的参数为最终结果，左右各半个周期时窗内（图8c 绿色短棒）的结果用于计算标准偏差.循环将每个台站作为参考点即可获得整个研究区域内地震波的传播参数（图9）.图9a 显示，作为古克拉通的四川盆地显示为高速异常，青藏高原由于地壳软弱物质的存在显示为低速特征；图9b-9d 显示的地震波传播参数与区域地质构造存在明显的关系（Cao et al.,2020）.图9e-9h 显示了T=40 s 地震波传播参数较小的标准偏差，在介质差异较大的块体边界和台站较稀疏的地方出现较大的标准偏差.

3.3 方位各向异性计算

循环每个地震事件便可以获得基于方位角变化的地震波传播参数，将基于方位角变化的瑞利面波相速度拟合到对应的方位各向异性模型即可获得对应的各向异性参数.由于川西台阵东面和南面地震射线覆盖较为密集，造成相速度在不同方位角上的覆盖密度出现很大的差异，根据瑞利面波相速度随反方位角呈180°的周期变化，将180°～360°反方位角映射到0°～180°的反方位角可以增加相速度的反方位角覆盖密度（图10a）.在各向异性拟合之前，为了增加有效值的权重，需要剔除奇异值（图10a 黑色圆圈），而取每10°后方位角内相速度的中值作为拟合数据可以均衡不同方位角相速度在拟合过程中的权重（图9b）.图10c 显示了不同区域方位各向异性的拟合结果.各向同性相速度由基于后方位角变化的相速度的中值给出，图11a 显示周期T=40 s 的Rayleigh 波在青藏高原东南缘的横向变化，总体特征与图9a 较为一致，但去掉了方位各向异性的影响.图11b 显示了不同台站的方位各向异性结果，总体上造山带和大型断层系统的走向相关，与SKS 和Pm 震相计算的各向异性较为一致（Cao et al.,2020）.Cao 等（2020）利用Bootstrap 方法评估了基于波场梯度法计算瑞利面波相速度方位各向异性的标准偏差，首先对图10a 基于方位角变化的相速度重采样1 000 次随机样本，评估随机样本拟合的1 000 个各向异性结果的离散程度获得了各向异性的标准偏差.图11c 显示了T=40 s 的Rayleigh 波相速度方位各向异性的标准偏差，各向异性强度和快波方向的标准偏差主要集中在1.5%和15°.

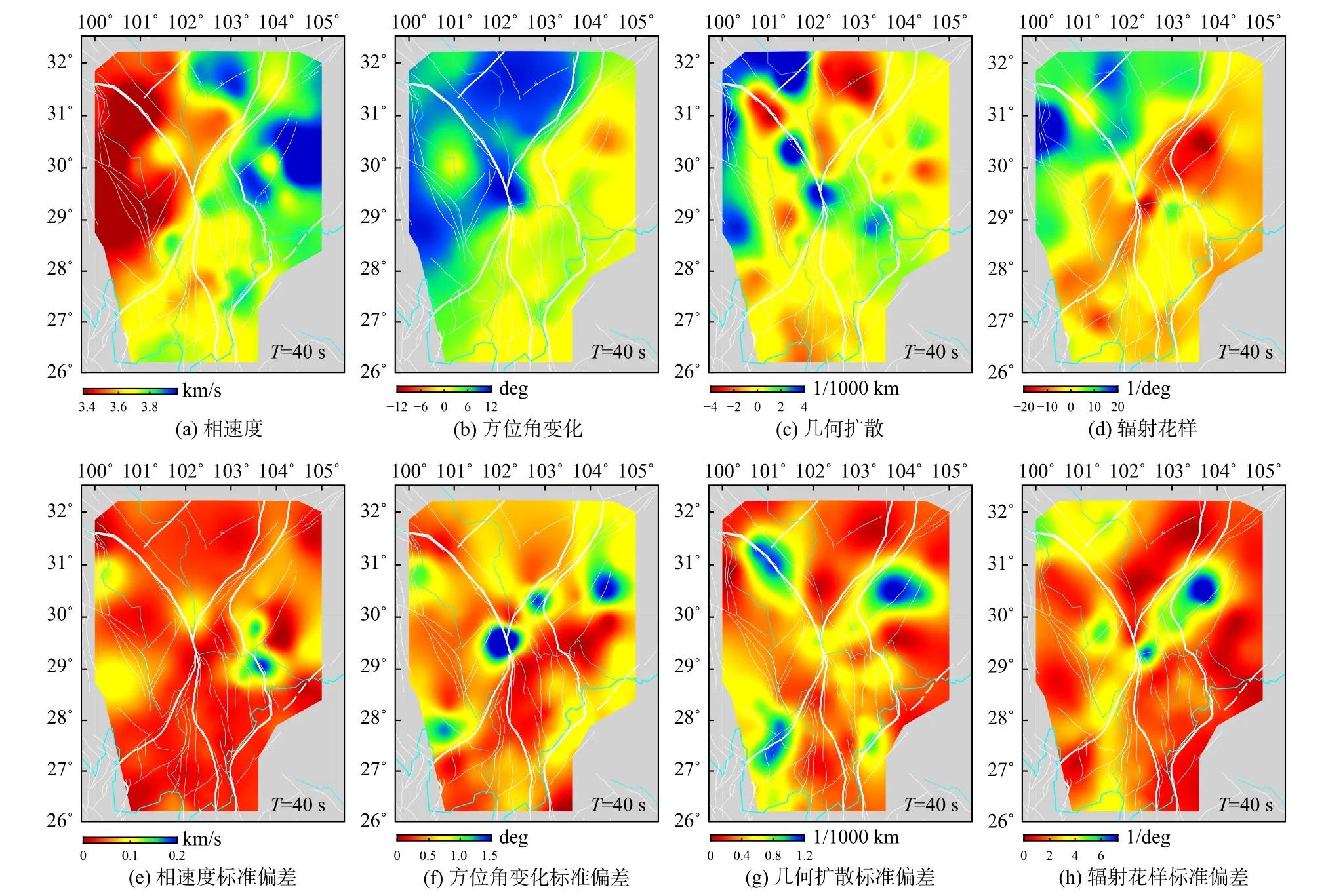
图9 基于波场梯度分析的2007 年8 月2 日鞑靼海峡M6.2 地震在川西地区的瑞利面波传播参数（a-d）及对应的标准差（eh），其中T=40 s，白色粗线为块体边界，白色细线为断层线，青色曲线为河流（修改自Cao et al.,2020）Fig.9 Rayleigh wave propagation parameters (a-d) and corresponding standard deviations (e-h) of the M6.2 Tatar Strait earthquake at T=40 s in the western Sichuan region based on wave gradiometry analysis.Thick and thin white curves represent block boundaries and faults,respectively,and cyan lines represent rivers (modified from Cao et al.,2020)

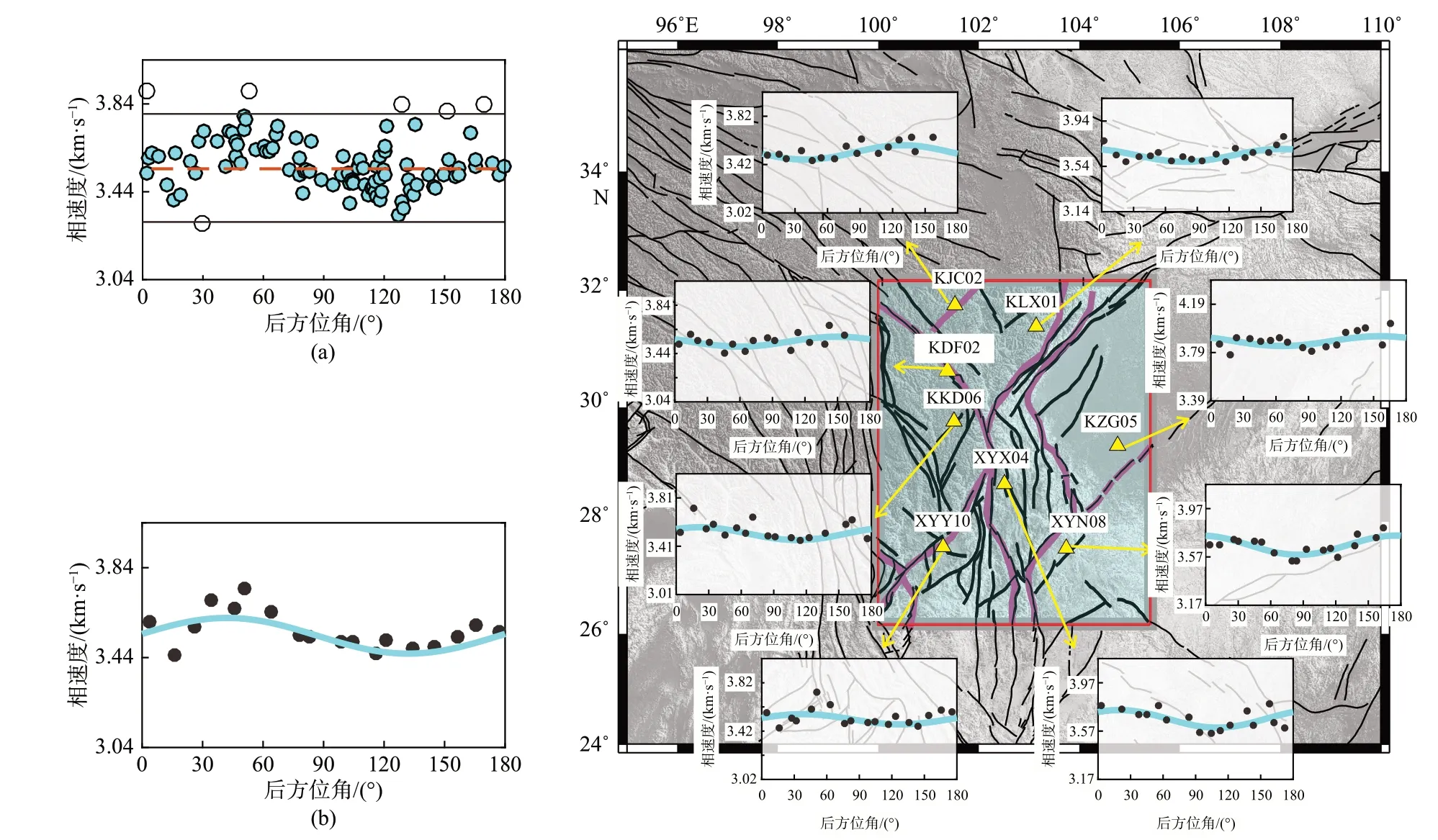
图10 青藏高原东南缘T=40 s 瑞利面波的方位各向异性拟合（修改自Cao et al.,2020）.（a）基于后方位角变化的相速度，黑色圆圈表示被删除的相速度，青色圆点为保留的相速度值，棕色虚线标记了各向同性相速度；（b）各向异性拟合，黑色圆点为每10°后方位角相速度的中值，青色曲线为方位各向异性最终的拟合结果；（c）不同区域的方位各向异性拟合的结果Fig.10 Azimuthal anisotropy fitting of Rayleigh surface waves at T=40 s (modified from Cao et al.,2020).(a) Azimuth-dependent velocity;black circles represent the discarded data points,cyan dots are the phase velocity used for anisotropy fitting,and the brown dotted line marks the isotropic phase velocity;(b) Anisotropy fitting;black dots are the median of the phase velocity in every ten-degree window of the back azimuth and the cyan curve is the final fitting result of azimuth anisotropy;(c) Fitting results of azimuthal anisotropy in different regions

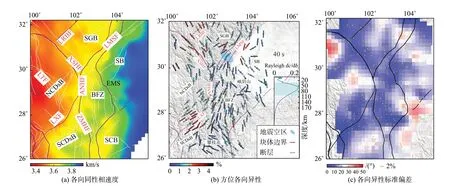
图11 青藏高原东南缘T=40 s 瑞利面波的各向同性相速度与方位各向异性结果.（a）瑞利面波各向同性相速度;（b）Rayleigh 波方位各向异性，短棒的方向代表快波方向，颜色代表各向异性强度，蓝色曲线为敏感核曲线；（c）各向异性标准偏差，底图表示快波方向标准偏差，黄色条的长度表示各向异性强度的标准偏差（修改自Cao et al.,2020）Fig.11 Isotropic phase velocity and azimuthal anisotropy of Rayleigh wave at T=40 s.(a) Rayleigh wave isotropic phase velocity.(b) Azimuthal anisotropy of Rayleigh waves,where the short bar direction represents the fast orientation,the color represents the anisotropic magnitude,and the blue curve represents the sensitivity kernel.(c) Anisotropic standard deviation,where the base represents the standard deviation of the fast orientation,and the length of the yellow bar represents the standard deviation anisotropic magnitude (modified from Cao et al.,2020)

4 与其他方法比较

4.1 波场梯度法与背景噪声成像对比

背景噪声成像是一种走时成像方法，通过互相关获取台站对的互相关函数，面波能量主要集中于5～40 s，射线密度对成像精度和稳定性产生重要影响；波场梯度法是一种基于波形随空间变化的密集台站地震成像方法，相对于背景噪声成像，考虑了相位和振幅的时空变化，可以进一步获得地震波的衰减信息.波场梯度法较依赖台站密度，台站密度对成像精度产生重要影响.

USArray 台间距为70 km，基于USArray，Porter等（2016）利用背景噪声成像和波场梯度法分别获取8～40 s 和20～150 s 瑞利面波相速度的频散.图12 显示了两种方法在重叠周期上成像的对比，可以看出两种方法获得的瑞利面波相速度大部分差异均小于0.05 km/s，而20 s 周期的对比结果相对于30 s 和40 s 周期的对比结果差异较大.

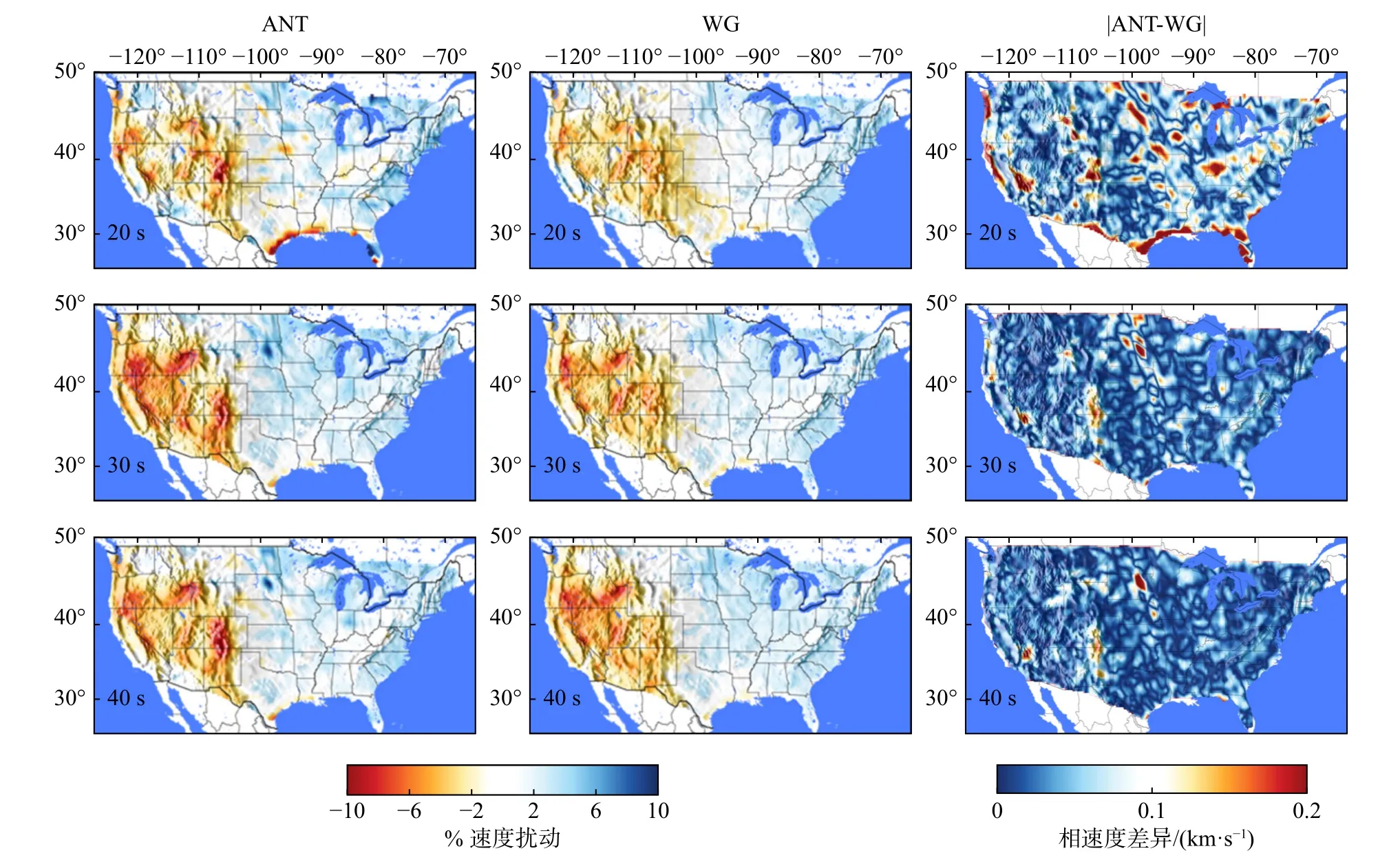
图12 美国大陆背景噪声成像和波场梯度法计算的瑞利面波相速度对比（修改自Porter et al.,2016）.ANT：背景噪声成像；WG：波场梯度法Fig.12 Absolute value images of differences between phase velocities calculated using ambient noise tomography and wave gradiometry (modified from Porter et al.,2016)

4.2 波场梯度法与程函方程成像对比

程函方程面地震波成像与波场梯度地震面波成像较为相似，都是基于密集台阵的成像方法，不同的是程函成像方法主要考虑的是地震波的走时信息（Lin et al.,2009）.

基于川西台阵，王怀富等（2020）利用程函方程面波成像获得不同周期瑞利面波的各向同性相速度方位各向异性.图13 显示了程函方程面波成像（EKN）和波场梯度法（WG）获得的相同（或相近）周期瑞利面波相速度和方位各向异性的结果，在20 s（或18 s）周期，这两种方法获得的相速度在四川盆地都大致分布在3.3～3.45 km/s，都表现为古克拉通的高速特征；在南川滇块体都大致分布在3.2～3.35 km/s，都表现为峨眉山大火成岩省的相对高速特征；在松潘甘孜块体的相速度均比北川滇块体高；各向异性强度均大致分布在1%～3%；在40 s 周期和60 s 周期，两种方法获得的相速度在正研究区域的异常分布也高度一致，四川盆地表现为高速，南川滇块体相对高速，松潘甘孜块体和北川滇块体表现为低速异常；两种方法获得的方位各向异性具有明显的一致性，特别是北川滇块体顺时针转向的快波方向和龙门山断裂带平行于断层走向的快波方向.基于USUArry，Jin 和 Gaherty（2015）利用程函方程地震面波成像获得了不同周期瑞利面波各向同性相速度结构（图14a-14c），Porter 等（2016）利用波场梯度法获得的地震面波相速度与该方法获得的相速度在相同周期上基本一致，比如在美国西部高原地区的低速异常和美国中东部地区的高速异常在空间分布上非常吻合（图14）.

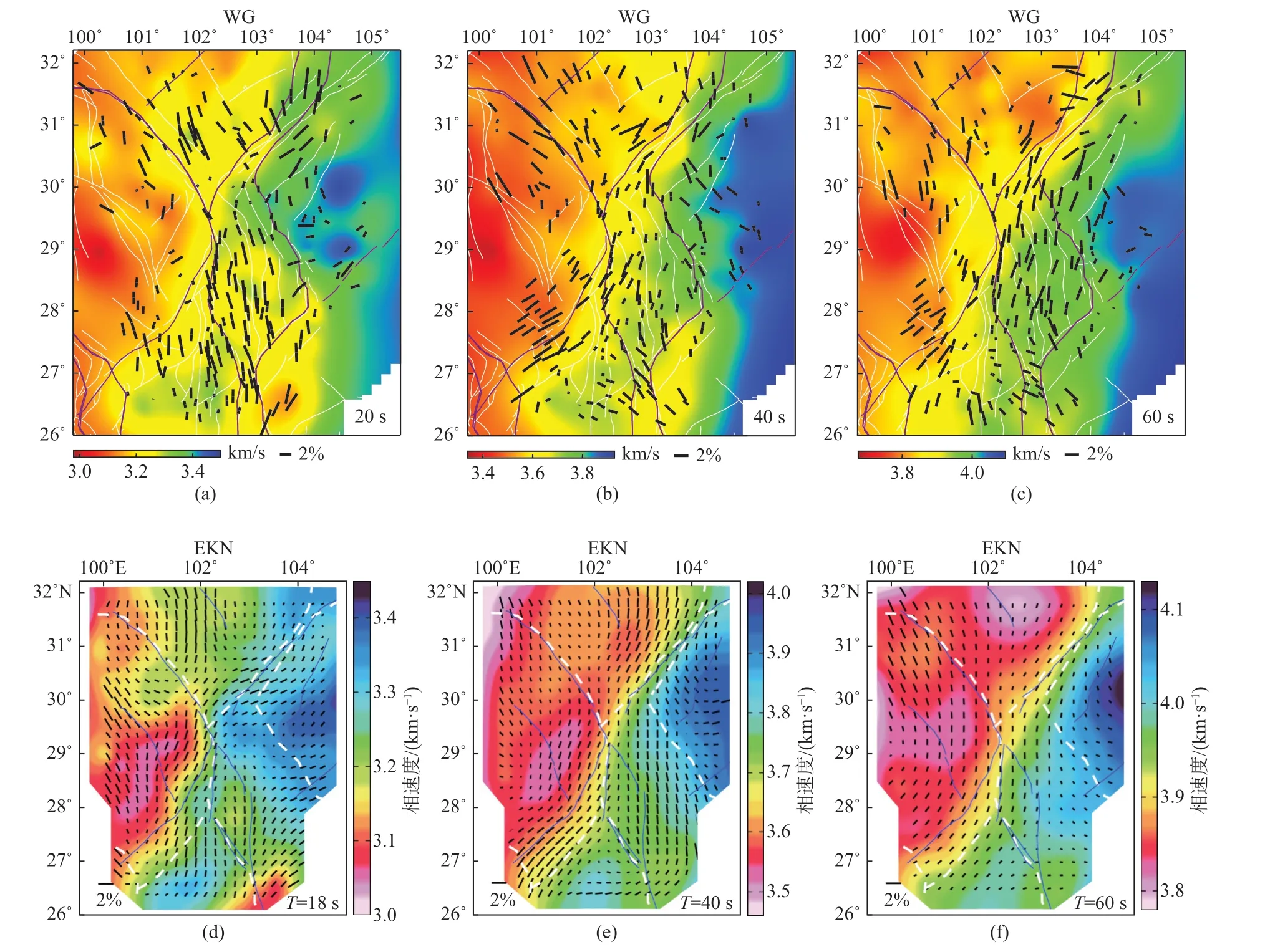
图13 青藏高原东南缘波场梯度法和程函方程面波成像获取的瑞利面波相速度和方位各向异性结果对比.（a-c）波场梯度法基于川西台阵获得的20 s、40 s 和60 s 周期的结果（修改自Cao et al.,2020）；（d-f）程函方程面波成像获得的18 s、40 s 和60 s 的结果（修改自王怀富等，2020）Fig.13 Comparisons of Rayleigh wave phase velocity and azimuthal anisotropy,as calculated by wave gradiometry and Eikonal tomography in the southeastern margin Tibetan Plateau.(a-c) Results at periods of 20,40,and 60 s calculated using wave gradiometry (modified from Cao et al.,2020);(d-f) Results at periods of 20,40,and 60 s calculated using Eikonal tomography (modified from Wang et al.,2020)

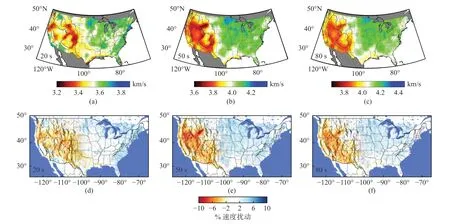
图14 美国大陆程函方程成像（a-c）（修改自Jin and Gaherty,2015）和波场梯度法（d-f）计算的瑞利面波相速度对比（修改自Porter et al.,2016）Fig.14 Comparisons of Rayleigh wave phase velocity calculated by Eikonal tomography (a-c) (modified from Jin and Gaherty,2015) wave gradiometry method and (d-f) in the North American continent (modified from Porter et al.,2016)

4.3 波场梯度法与接收函数在方位各向异性计算上的对比

基于川西台阵，Zheng 等（2018）利用基于方位角变化的S 波接收函数Pms 震相计算了青藏高原东南缘地壳的平均方位各向异性.与波场梯度法相比，该研究主要获得的是地壳的平均各向异性，而WG 方法可以获得反映不同深度的结果.图15显示了波场梯度法获得的20 s 瑞利面波相速度的各向异性与接收函数Pms 震相获得的各向异性的比较，根据敏感核曲线20 s 和40 s 周期瑞利面波的各向异性主要体现的分别是25 km 和50 km 深度上的结果；玫瑰统计图显示20 s 和40 s 周期瑞利面波与Pms 震相的快波方向差异中值分别为40°和25°；从不同的区域来看，两种方法获得的各向异性在松潘甘孜块体和北川滇块体具有较为一致的快波方向，而20 s 周期的瑞利面波快波方向在四川盆地、板块边界断层带（BFZ）和南川滇块体与Pms震相的快波方向具有较大差异（图15a 黄色阴影区），40 s 周期的瑞利面波快波方向在BFZ 与Pms 震相的快波方向存在较大差异（图15b 黄色阴影区）.这种差异可以由以下几个原因造成：（1）S 波接收函数相对于瑞利面波频率较高，而不同频率的地震信号可能敏感于不同尺度或规模的各向异性体（Faccenda et al.,2019;Wang et al.,2013）；（2）不同深度上各向异性介质差异较大，这时代表地壳平均水平的Pms 震相的各向异性与敏感于中上地壳的20 s 周期瑞利面波的各向异性就会出现较大差异.

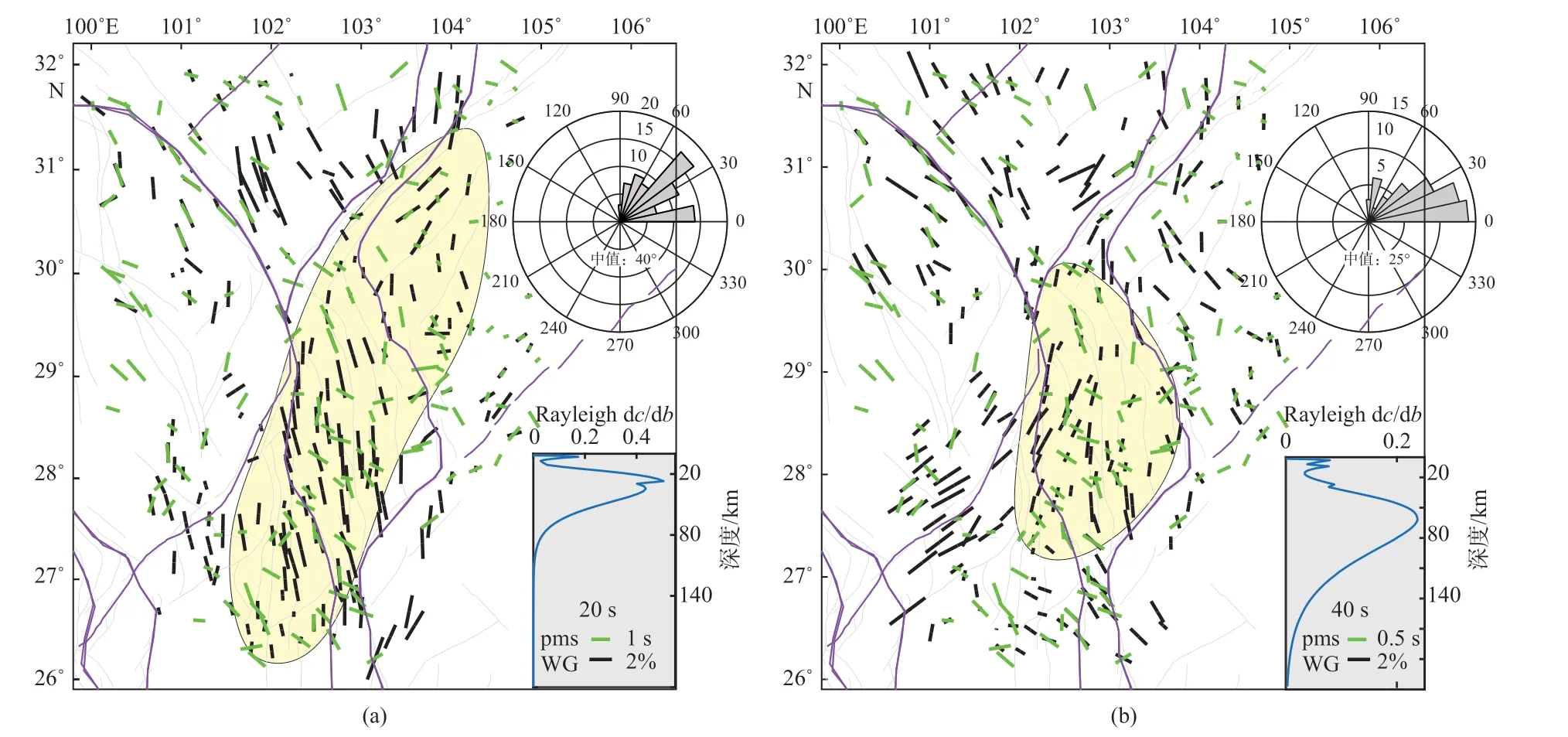
图15 青藏高原东南缘波场梯度法和接收函数Pms 震相计算的各向异性比较（修改自Cao et al.,2020）.每个子图的玫瑰图统计了两种方法获得的各向异性在快波方向上的差异；右下方的蓝色曲线为敏感核曲线；黑色短棒为波场梯度法获得的方位各向异性结果（来自Cao et al.,2020）;图（a）和图（b）绿色短棒为接收函数Pms 震相获得的方位各向异性（来自Zheng et al.,2018）,黄色阴影区标记了方位各向异性差异较大的区域Fig.15 Comparisons of anisotropy calculated using wave gradiometry and Pms phase of receiver function in the southeastern margin Tibetan Plateau (modified from Cao et al.,2020).Rose diagrams indicate the statistics of fast-orientation differences in two methods;blue curves denote the sensitivity kernel,black bars represent the results from wave gradiometry (from Cao et al.,2020),green bars are the results obtained by the Pms phase (from Zheng et al.,2018),and the yellow shadow marks the area with relatively large difference in fast propagation direction between the two methods

5 结论与展望

本文介绍了波场梯度法发展历史、方法原理、反演技术和应用.总的来说，波场梯度法适用于不同类型的密集台阵（台间距不超过一个波长），适用于P 波（Langston,2007a;Langston and Liang,2008）、S 波（Langston,2007b;Langston and Liang,2008;Sollberger et al.,2016）、面波（Langston and Liang,2008;Liang and Langston,2009）和背景噪声（de Ridder and Curtis,2017）的波场梯度分析.尽管在方法技术上已经得到较好的发展，在大尺度深部结构反演方面也得到了很好的应用，而随着密集台阵的不断发展，作为一种较新的地震数据处理方法，波场梯度法在应用方面还不够广泛，将波场梯度法应用于更多研究是一种新的尝试.比如在通过梯度分析活动断裂破裂前的地震波场时空特性（传播方向和振幅变化等）来检测断层的动态破裂过程以评估大震的风险性（Langston,2007b），通过更多的密集台网对全球大型构造成像以研究全球的地球动力学过程等.

另外，波场梯度法在技术创新上仍有发展空间.密集台阵可以记录地震波空间上更完备的区域传播特征，而基于密集台阵的波场梯度法充分考虑了地震波场振幅和相位在空间上的变化，可以计算更多的地震波传播参数.这些参数尽管已经被应用于应力、应变、衰减、速度成像、各向异性或到时拾取，而该方法在以下几个方面还有发展的空间：

（1）衰减结构反演

如何从波场梯度反演的几何扩散提取介质的衰减参数研究地球内部的衰减特性技术问题仍然有待开发.尽管Langston 和 Ayele（2016）通过波场梯度法已经获得了体波在地球内部的衰减因子Q，但三维衰减结构反演技术还有待进一步发展.

（2）径向各向异性结构反演

周鲁等（2017）计算了三分量的波场梯度，并获得了Rayleigh 波和Love 波的相速度.如何结合二者的相速度计算径向各向异性也是未来可以改进的方向.

（3）多数据联合反演

不同地震数据对介质物性的约束有所差异，通过不同地震数据的联合反演来约束模型的多解性是一种较为流行的做法（Liu et al.,2014;Liu et al.,2018;Porter et al.,2016;Yang et al.,2011）.对于波场梯度法来说，相同密度的台站分布，波场梯度法可以获得较为低频的地震波相速度，环境噪声互相关可以获得较为高频的地震波速度，而接收函数相对于面波成像对介质的速度界面较为敏感.那么，这三种数据的联合反演对三维S 波速度和方位各向异性可以提供更好的约束，而基于方位角变化的频散曲线反演方法（ADDCI,Liang et al.,2020）的成功应用为这种联合反演提供可能.总而言之，充分考虑地震波更多的时空信息和联合更多的地球物理数据研究地球动力学过程是今后的地球物理的发展趋势.