基于面波走时的三维结构面波直接成像：方法综述与应用

姚华建，罗 松，李 成，胡少乾，方洪健

1 中国科学技术大学地球和空间科学学院，合肥 230026

2 蒙城地球物理国家野外科学观测研究站，蒙城 233500

3 安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，淮南 232001

4 中国地质大学（武汉）地球物理与空间信息学院，武汉 430074

5 中山大学地球科学与工程学院，珠海 519080

0 引言

面波是沿地球表面传播的一种地震波，与在地球内部传播的体波相对应，是研究地壳上地幔速度结构和地震震源机制的一种非常重要的地震波.根据偏振方向的差异，面波可以主要分为瑞利（Rayleigh）面波和勒夫（Love）面波.瑞利面波的质点运动轨迹呈现为椭圆形，且垂向和径向的瑞利面波相位相差90°；勒夫面波在与传播方向垂直的水平面上运动.瑞利面波传播的速度主要对地下不同深度介质沿垂直方向偏振的SV 波的速度（VSV）比较敏感，对纵波速度和密度有较弱的敏感性.勒夫面波传播的速度主要对地下不同深度沿水平方向偏振的SH 波的速度（VSH）敏感，对密度具有较弱的敏感性.不同周期面波的敏感深度不一样，通常周期越长的面波穿透深度越深；因此相对于短周期面波，长周期面波对深部介质具有更强的敏感性.且由于不同深度介质的速度存在差异，因此导致不同周期的面波具有不同的传播速度，这就是面波的频散.通过提取面波的频散信息，我们可以反演地壳上地幔的横波速度结构.

时频分析方法（例如,Dziewonski et al.,1969;Landisman et al.,1969;Levshin and Ritzwoller,2001;Yao et al.,2005）被广泛应用于测量事件到台站或者双台之间的面波频散曲线，包括群速度（U）频散和相速度（C）频散.波形反演方法也常被用于获得事件到台站之间的相速度频散曲线（例如,Trampert and Woodhouse,1995;Van Heijst and Woodhouse,1999;Woodhouse and Dziewonski,1984），但需要考虑地震时间的初始相位问题.基于地震事件得到的频散曲线一般周期在10 s 之上，长周期可达300 s，但10 s 以内的短周期频散曲线难以提取，主要是由于短周期面波受复杂上地壳结构的散射及较强的衰减影响较大.因此，基于地震事件提取的面波频散通常难以获得上地壳或中上地壳的精细结构.本世纪初，一系列研究发现连续背景噪声互相关方法可以有效地恢复台站之间的中短周期面波信号（例如,Sabra et al.,2005;Shapiro and Campillo,2004;Shapiro et al.,2005;Yao et al.,2006），从而大大促进了中短周期面波频散曲线的可靠提取，显著提升了中上地壳（甚至地壳浅层）结构成像的可靠性和分辨率.

1950 年代起，单台法（或双台法）已经被广泛用于测量地震事件到台站（或双台之间）的面波频散曲线，并被用于反演路径上的或不同区域平均的地壳上地幔层状横波速度结构模型（例如,Brune and Dorman,1963;Knopoff et al.,1966;Press,1957）.从1980 年代起，基于面波频散数据地震学家发展了面波层析成像方法（例如,Barmin et al.,2001;Montagner and Jobert,1988;Montagner and Nataf,1986,1988;Ritzwoller and Levshin,1998;Tanimoto,1986a,1986b;Trampert and Woodhouse,1995），即两步法面波成像：第一步先通过面波走时成像反演获得不同周期的二维相速度（或群速度）分布图，第二步是基于每个格点的纯路径频散反演格点下方一维层状横波速度模型，然后将所有格点的一维模型拼合起来得到研究区域的三维横波速度模型.基于地震面波提取的中长周期面波频散和背景噪声面波提取的中短周期面波频散可以有效地融合，得到从短周期到长周期的面波频散资料，从而有效约束地壳上地幔的三维横波速度结构（例如,Yang et al.,2008;Yao et al.,2006,2008）.目前无论是三维各向同性横波速度结构的面波成像，还是方位各向异性横波速度结构的面波成像（例如,Montagner and Jobert,1988;Yao et al.,2010），以及径向各向异性横波速度结构的面波成像（例如,Huang et al.,2010;Luo et al.,2013;Shapiro et al.,2005），主要采用两步法模式.

面波两步法成像中的第一步，即面波二维相速度或群速度成像，通常基于面波射线理论，且绝大部分研究直接假设面波沿大圆路径传播，即不同周期面波均沿着从事件到台站之间的最短大圆路径传播，忽略路径上的结构异常对面波传播路径的影响.当面波二维相速度分布横向变化不大时（例如低于10%），基于大圆路径假设与基于面波射线路径路径追踪方法得到的二维相速度成像结果几乎相同，但当相速度横向变化较大时（例如高于20%），通常会造成基于大圆路径假设得到的二维相速度成像结果存在一定的偏差（李想等，2015）.因为短周期面波对地壳浅层结构非常敏感，当研究区域浅层结构横向变化很大时，短周期二维相（群）速度成像需要采用基于面波射线路径追踪（Rawlinson and Sambridge,2004）的走时成像方法（Young et al.,2011），即需要考虑到射线路径弯曲对面波走时计算的影响.

当面波频率较低（或波长较长），以及异常体的横向尺度与面波波长相当时，通常需要考虑面波传播的有限频效应，才能够更为准确地反演结构异常.一些研究基于散射理论提出面波走时扰动计算的二维有限频敏感核（sensitivity kernel）方法（例如,Spetzler et al.,2002;Yoshizawa and Kennett,2005），相对于基于射线路径的面波走时扰动计算方法可以更好地预测面波走时异常，目前已经被应用到区域和全球范围内的二维面波相速度成像研究中（例如,Ritzwoller et al.,2002;Yang and Forsyth,2006;Yoshizawa and Kennett,2004）.值得注意的是，二维敏感核计算时需要计算面波走时，而面波走时通常是基于大圆路径计算得到的.但当介质存在较强的横向非均匀性时，除了有限频效应外，由于射线路径弯曲所导致的走时异常是不能被忽略的（Yang and Hung,2005）.

当台站分布较为密集且均匀时，通过事件（或背景噪声虚拟源）到台站的面波数据和台阵分析方法可以有效构建不同周期的二维相速度分布图，例如采用基于面波走时的程函方程成像方法（Lin et al.,2009），基于面波走时和振幅的亥姆霍兹方程成像方法（Helmholtz tomography,Lin and Ritzwoller,2011），以及面波波形梯度成像方法（wave gradiometry,Liang and Langston,2009）.程函方程成像方法通过计算走时的梯度场可以获得面波的传播方向和路径，即该方法考虑了面波传播路径的弯曲效应.由于亥姆霍兹方程成像和面波波形梯度成像方法还使用了面波振幅或波形信息，因此可以同时考虑面波的射线路径弯曲效应和有限频效应，在理论上具有更高的成像精度.

无论是基于面波走时的成像反演或台阵面波成像方法，构建了不同周期的二维相速度（或群速度）分布图后，都需要进一步得到反演区域各网格点的纯路径频散，然后通常采用单点频散曲线反演的方法获得格点下方的一维层状横波速度模型.由于每个格点的层状横波速度反演是独立的，格点与相邻格点之间的模型并没有横向平滑约束，可能会导致最后拼合得到的三维模型出现一些横向假异常.此外，当有的周期路径分布较稀疏时，往往难以得到该周期可靠的相速度（或群速度）分布图，这些数据便无法用于反演三维横波速度模型.

为了避免面波两步法成像存在的问题，一些学者提出面波一步法成像，即基于测量得到的所有路径面波频散走时数据直接反演三维横波速度模型的面波直接成像方法（Boschi and Ekström,2002;Fang et al.,2015;Feng and An,2010）.Boschi 和Ekström（2002）以及 Feng 和An（2010）提出的方法并不考虑面波路径的弯曲效应，在反演过程中面波始终沿大圆路径传播，因此对横向非均匀性很强的速度结构反演会存在一定的误差，例如近地表或地壳起伏变化很大的地区.而Fang 等（2015）提出的面波直接成像方法（direct surface wave tomography,DSurfTomo）考虑了不同周期面波路径的弯曲效应，反演是一个逐步迭代的过程，每次迭代模型更新后会重新计算不同周期的面波射线路径及面波走时的分辨核矩阵，从而使得反演结果更为可靠和准确.基于Fang 等（2015）发展的各向同性面波直接成像方法，Liu 等（2019）进一步发展了基于瑞利面波频散走时直接反演三维横波速度方位各向异性模型的成像方法（DAzimSurfTomo），Hu 等（2020）进一步提出了基于瑞利面波和勒夫面波频散走时数据直接反演三维横波速度径向各向异性模型的成像方法（DRadiSurfTomo）.这些新的面波直接成像方法可以避免构建二维相速度或群速度分布图，且同时对不同周期的面波路径分别进行射线追踪，避免了常规面波走时成像的大圆路径传播假设，更好地考虑了结构异常对射线路径及最终模型反演的影响，可以获得更为可靠的三维各向同性及各向异性的横波速度结构模型.

本综述论文将首先阐述面波两步法成像的基本原理，然后详细介绍面波直接成像方法，之后再通过几个具体实例来展示面波直接成像方法在不同尺度结构成像中的应用，最后对面波直接成像方法的若干问题和发展方向进行讨论与展望.

1 面波两步法成像基本原理

在传统的面波成像中我们通常假设面波沿着大圆路径传播，然而在强横向非均匀介质中，面波路径会偏离震源和接收台站之间的大圆路径.在高频近似的情况下，角频率为 ω的面波走时可以表示为：

其中S(l,ω)是震源和接收台站AB 之间的实际射线路径的局部慢度.公式（1）可以表达为离散形式：

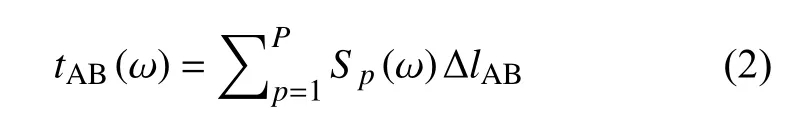
其中Sp为沿AB 的射线路径段 ΔlAB上的相位慢度，p是路径段的编号（如图1a 所示）.公式（2）可以进一步表示为：

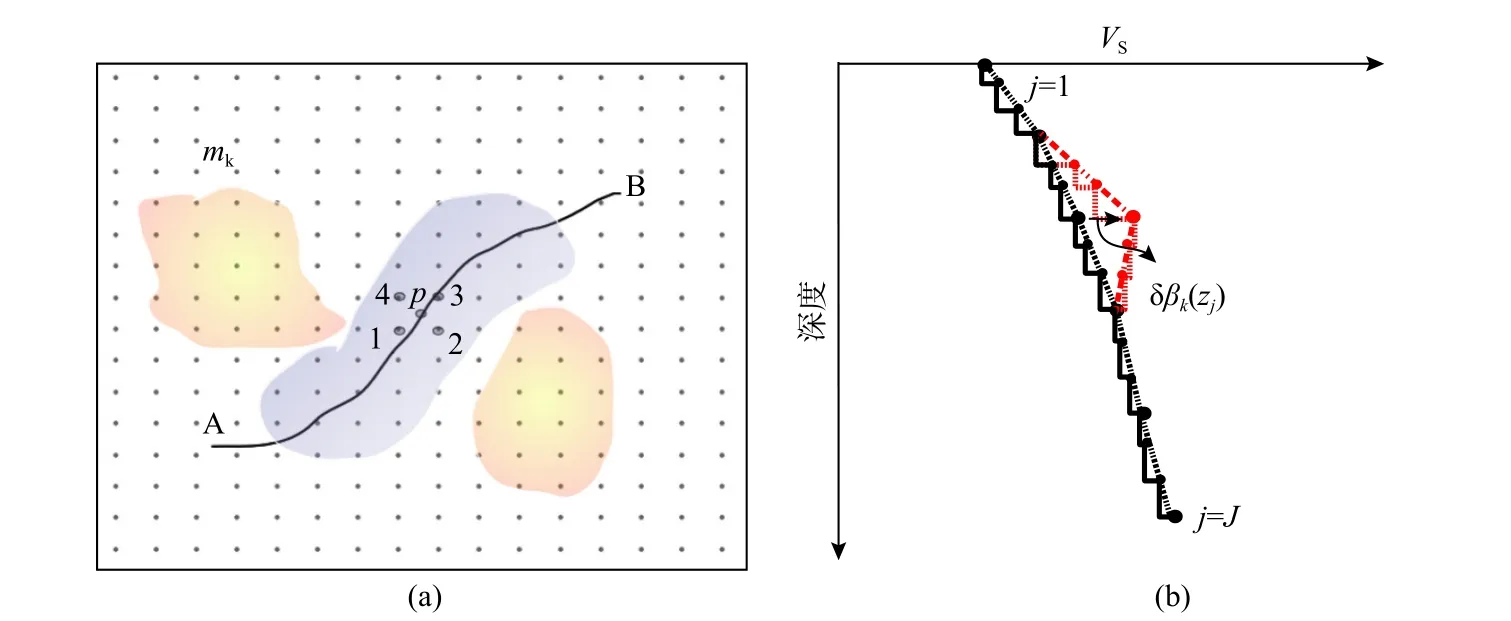
图1 面波成像中离散化的三维网格点模型及面波射线路径示意图.（a）水平向的二维慢度网格点；（b）垂直向的VS 网格点（黑点）和插值得到的层状模型（黑色阶梯状实线）.图（a）中的黑色实线表示某个周期面波在AB 间的传播路径，路径上的p 点的慢度由周围4 个水平网格点（1、2、3、4）的双线性值插值获得.图（b）中垂直格点模型通过扰动（如红色圆点和虚线所示）来计算频散相对于参数模型的深度敏感核（修改自Fang et al.,2015）Fig.1 Discretized 3D grid model of surface wave tomography and illustration of surface wave ray path.(a) 2D slowness grids in the horizontal direction;(b) VS grids (black dots) in the vertical direction and the interpolated layered model (black staircase lines).In (a) the black solid line represents the propagation path between two stations A and B for the surface wave at some period.The phase slowness at any point p along the path is determined from the values at four surrounding horizontal grid points (1,2,3,4) using a bilinear interpolation method.In (b) the vertical grid model is perturbed (as shown by the red dots and red dashed lines) to compute the depth sensitivity kernel of dispersion data to model parameters (modified from Fang et al.,2015)

基于测量得到的面波相速度或群速度曲线，我们可以获得相对应的频散走时tAB(ω)，然后采用基于连续模型的非线性反演方法（Montagner and Nataf,1986;Torantola and Valette,1982）来反演各个周期的二维相速度或群速度分布图.反演的目标函数定义为：

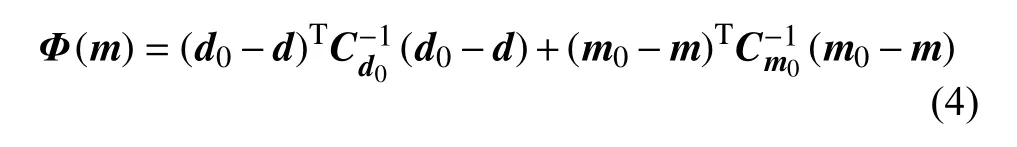
其中d0是测量得到的同一频率、不同路径的面波走时向量，d是通过d=g(m)公式[例如（2）式]与给定的研究区域二维相速度（或慢度）模型m计算得到的理论走时向量，m0是初始相速度（或慢度）模型向量；Cd0是描述数据不确定度的数据协方差矩阵，通常是一个对角矩阵，对角线元素为（第i条路径走时测量误差）的平方；Cm0是模型的先验协方差矩阵，通常取为高斯型的协方差矩阵，使得反演得到的二维相速度或群速度模型在空间上达到一定横向尺度的平滑.这里模型m可以仅为各向同性相速度（或群速度）参数，也可以包含方位各向异性参数（例如,Barmin et al.,2001;Montagner and Nataf,1986）.

除了采用基于连续模型的非线性反演方法来求解（4）式外，Backus-Gilbert 方法（Yanovskaya and Ditmar,1990）、基函数展开（Trampert and Woodhouse,1995）等反演方法也常用于反演二维相速度（或群速度）分布图，这里就不一一赘述.通过不同周期反演得到的二维相速度或群速度分布图，我们可以获得反演区域每个格点的纯路径频散曲线，然后基于纯路径频散曲线进一步反演格点下方的层状速度结构模型，最后将所有二维面状格点下方的一维模型拼合成为三维速度结构模型.从单点频散反演一维层状速度模型通常采用非线性问题的线性迭代反演方法（例如,Herrmann,2013）或者全局优化反演方法（例如,Shapiro and Ritzwoller,2002;Yao et al.,2008）.由于瑞利面波频散主要对垂直方向偏振的横波速度VSV敏感，对密度ρ和纵波速度VP的敏感度不高，通常在反演时采用经验关系式将 ρ和VP与VSV耦合在一起，从而仅反演层状VSV结构（例如,Yao et al.,2008）.

勒夫面波主要对水平方向极化的横波速度VSH敏感，对 ρ的敏感性较小，因此可以用于反演层状VSH速度结构模型.在同时具有瑞利面波和勒夫面波频散数据时，我们可以同时或分别反演获得VSV和VSH速度结构（例如,Shapiro and Campillo,2004;Huang et al.,2010），再进一步获得介质的径向各向异性参数，例如γ=VSH/VSV，或者ξ=2(VSHVSV)/(VSH+VSV).

对于面波方位各向异性的两步法成像，通常采用基于连续模型的非线性反演方法（Montagner and Nataf,1986;Torantola and Valette,1982）同时反演各个周期的各向同性相速度和方位各向异性参数，之后再反演每个格点上的纯路径方位各向异性频散曲线，获得格点下方的横波速度及其方位各向异性参数（Montagner and Nataf,1986）.Smith 和Dahlen（1973）通过研究发现弱弹性各向异性介质可以引起瑞利波和勒夫波相速度的方向依赖性，并在不考虑 4Ψ项（Ψ 为面波传播方位角）的影响下，位置在M处、角频率为 ω的瑞利面波相速度c(ω,M,Ψ)可表示为如下的近似表达式：

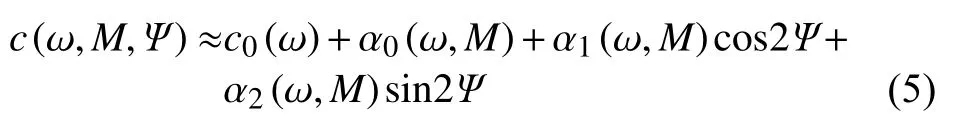
其中c0(ω)为参考相速度，α0(ω)是各向同性相速度扰动，α1(ω)和α2(ω)是方位各向异性参数，A=分别是该频率下瑞利面波方位各向异性的强度大小和快波方向.

根据Montagner 和Nataf（1986），M处的瑞利波相速度扰动δc(ω,M,Ψ)可以近似表示为：

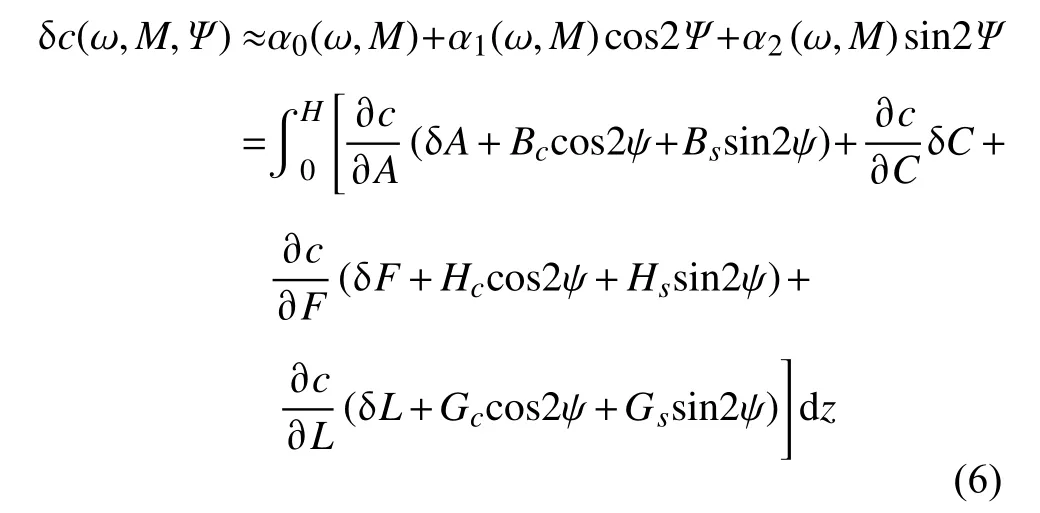
公式（6）中A、C、F、L和N用来描述具有垂直对称轴的横向各向同性介质（VTI）的弹性参数，其 中F=η(A-2L)，VPH和VPV分别是沿水平和垂直方向传播的P 波速度，VSH和VSV分别是沿水平和垂直方向极化的S 波速度.另外的六个参数Bs,c、Gs,c和Hs,c分别给出了弹性参数A、L、F的 2ψ项方位变化.敏感核∂c/∂pi（pi分别是A、L或F）可由一维参考模型计算获得（Montagner and Nataf,1986）.

Montagner 和Nataf（1986）发现∂c/∂L项在公式（6）中贡献最大，∂c/∂A项在地壳中相对较大，而在上地幔中可忽略不计（图2）.∂c/∂F项较小，因此在实际反演中常忽略∂c/∂F项.（6）式的反演可以基于线性反演方法（Montagner and Nataf,1986），首先基于某一参考模型计算∂c/∂pi，然后再反演（6）式中相关参数，主要是L和Gs,c；或者基于全局优化的反演方法，例如Yao（2015）提出基于邻域算法的方位各向异性横波速度模型反演方法.

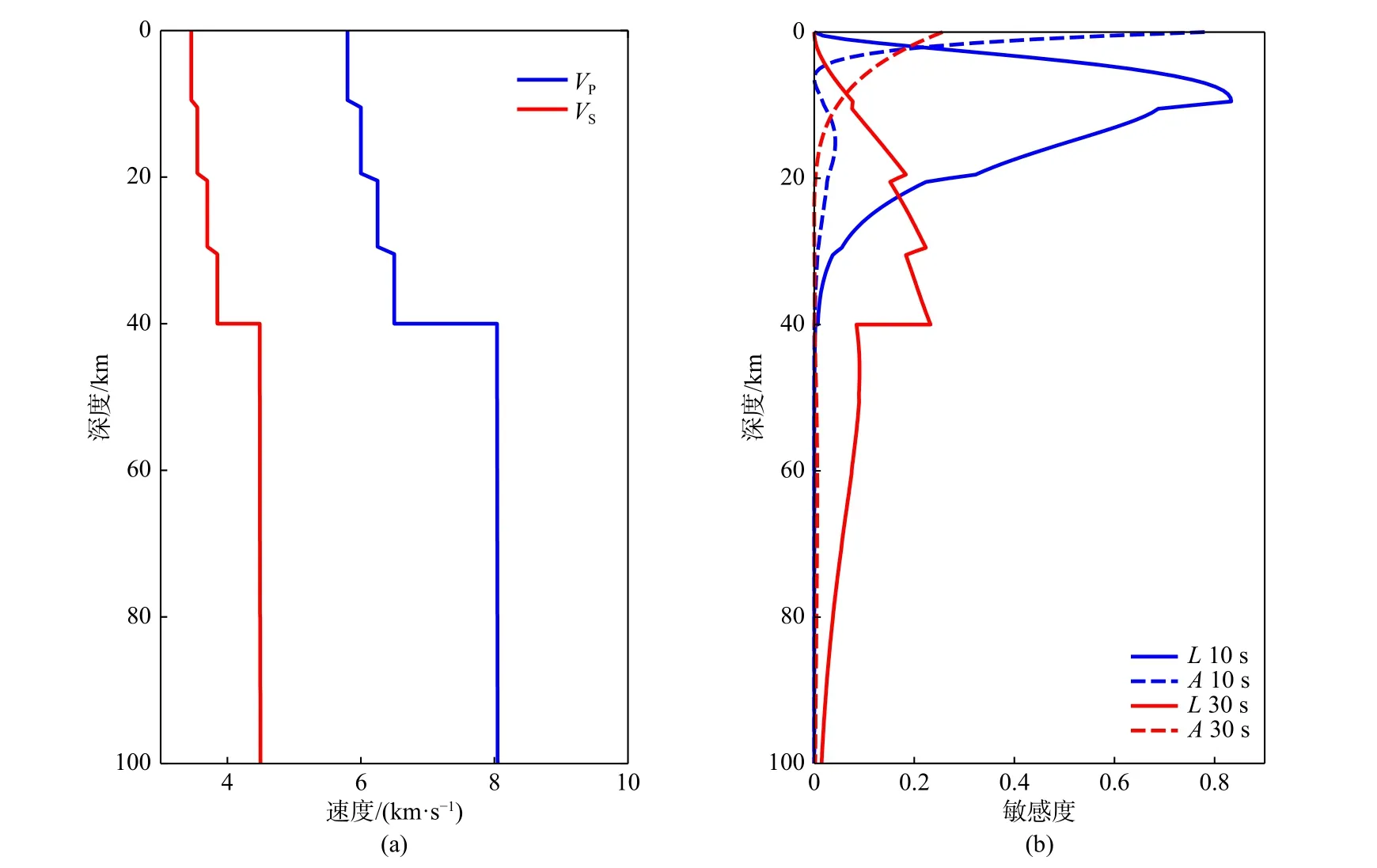
图2 一维速度模型（a）及其相应的d c/dL（实线）和d c/dA（虚线）在不同周期的深度敏感核（b）（修改自Liu et al.,2019）Fig.2 Depth sensitivity kernels (b) of dc/dL (solid line) and dc/dA (dashed line) at different periods from a 1D velocity model (a)(modified from Liu et al.,2019)

最后，垂向方向偏振的方位各向异性横波波速可以表示为：

由于Gc,s通常远远小于L，即，因此，（7）式可以近似表示为：

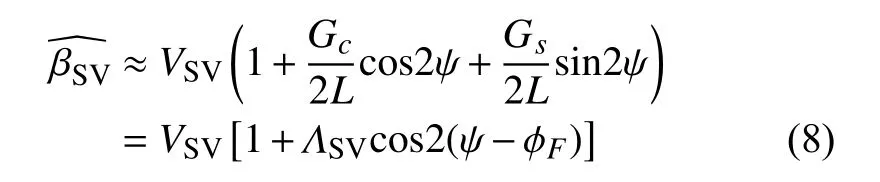
其中ΛSV和ϕF分别是VSV的方位各向异性振幅大小和快轴的方位角：

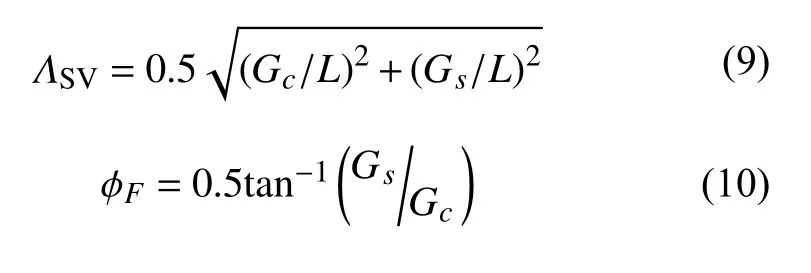
2 面波直接成像方法

在第1 节中我们阐述了面波两步法成像的基本原理和常用方法，本节我们将系统阐述面波直接成像方法（即面波一步法成像）的原理，主要基于我们近些年发展的考虑不同周期面波射线路径追踪的面波直接成像方法体系，包括直接反演三维各向同性横波速度（VS）模型的成像方法（DSurfTomo,Fang et al.,2015）、直接反演三维横波速度（VSV）及其方位各向异性模型的成像方法（DAzim-SurfTomo,Liu et al.,2019），以及直接反演三维横波速度结构及径向各向异性模型的成像方法（DRadiSurfTomo,Hu et al.,2020）.三种面波直接成像方法的简介如图3 所示.

图3 面波直接成像方法（DSurfTomo、DAzimSurfTomo和DRadiSurfTomo）的简介图Fig.3 The sketch diagrams of the direct surface wave tomography methods (DSurfTomo,DAzimSurfTomo,and DRadi-SurfTomo)

2.1 三维各向同性横波速度模型反演的面波直接成像方法

我们将地下三维结构离散为三维网格点，包括水平向的网格点（图1a）和垂向的网格点（图1b），垂向的层状速度模型可以通过垂向网格点插值来获得.源A 和台站B 之间的面波走时（频率为 ω）可以（3）式来表示，这里考虑由于二维面波相速度的横向非均匀性导致的面波传播路径的弯曲效应，即偏离传统假设的大圆路径（图1a）.

对于一维层状结构模型（图1b），相速度的扰动可以表示为：

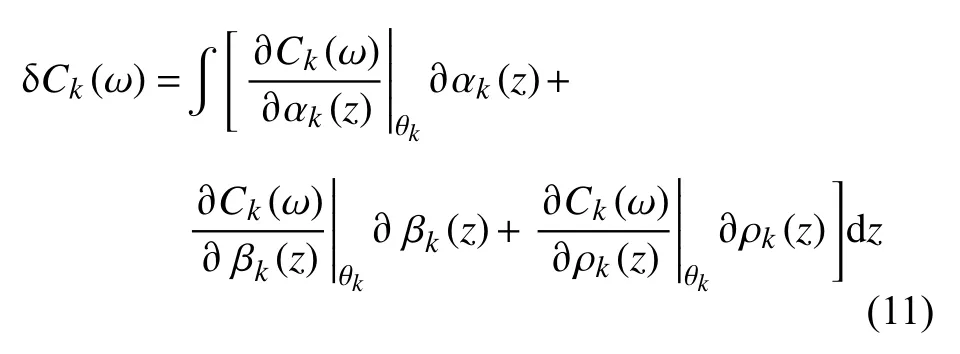
其中 θk表示一维层状参考模型，αk(z)、βk(z) 和ρk(z)分别是纵波速度、横波速度和密度.根据Brocher（2005）提出的经验公式，我们可以将纵波速度和密度用横波速度的来表示.基于（3）式，观测面波到时与理论面波到时的残差可以表示为：

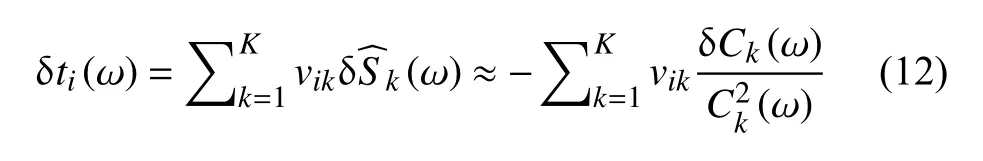
将（12）式带入（11）式，同时利用Brocher（2005）经验公式，我们得到：

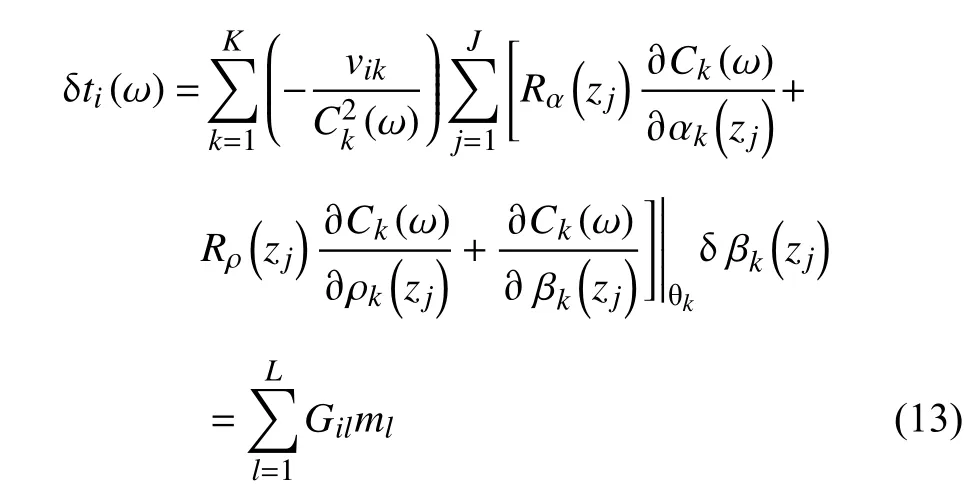
我们构建的反演问题的目标函数为：

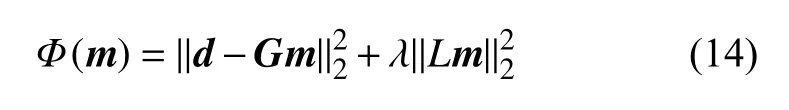
其中，右边第一项为数据残差项（基于L2 范数），第二项为模型正则化项（基于L2 范数），L是模型平滑算子，这里我们通常选用一阶Tikhonov 模型正则化约束，λ是用来平衡数据拟合和模型平滑的权重参数，通常采用L-curve 方法来确定（Aster et al.,2013）.公式（14）所示的反演问题可以通过LSQR 算法（Paige and Saunders,1982）求解.基于（14）式，我们可以反演求解得到三维网格点的横波速度模型的扰动量，之后得到新的三维横波速度模型，纵波速度和密度再通过与横波速度的经验公式（Brocher,2005）来计算获得.之后，我们会基于更新的三维模型重新计算不同周期的相速度分布图，然后采用快速行进方法（Rawlinson and Sambridge,2004）来计算不同周期面波的射线路径，之后再更新G矩阵以及反演得到下一次模型的更新量，如此迭代直到反演结果收敛.

除了常规的基于Tikhonov 模型约束的反演方法外，Fang 等（2015）还提出了一种基于小波基函数稀疏反演的策略来求解（14）式，可以实现多尺度的模型分辨.Fang 等（2015）的反演方法基于预先设定的一套三维网格点，Luo 等（2021）在此基础上进一步提出基于多套交错网格的面波直接成像方法，通过不同网格反演得到的模型可以获得最终平均模型以及模型的误差估计，测试结果也显示基于多套交错网格的反演方法有助于提升模型的分辨率.

在传统的面波两步法成像中需要构建不同周期的二维相速度和群速度分布图，但在有些情况下由于某些周期的路径较少，难以获得可靠的二维相（群）速度分布图，因此这些周期的数据无法用于两步法成像中.但在直接反演方法中，所有周期的频散走时测量数据均可以用于成像中，提升了数据的利用率和路径覆盖密度，从而有助于提升成像的分辨率.且由于每个周期每条路径的面波射线路径都分别计算获得，可以更好地考虑复杂介质（尤其是地壳浅层）对不同周期面波走时测量的影响，有助于提升反演结果的可靠性.

虽然面波频散对纵波速度和密度的敏感性要明显低于对横波速度的敏感性，但直接忽略纵波速度和密度的影响也会影响横波速度的反演结果，尤其是瑞利面波频散对浅层地壳纵波速度敏感性也比较大.因此，面波直接成像方法在频散走时敏感核矩阵的构建时考虑到了纵波速度和密度对面波频散的影响，通过经验公式将纵波速度和密度与横波速度耦合在一起，从而将纵波速度和密度对频散数据的敏感核转变为对横波速度的敏感核[公式（13）]，进一步提升了横波速度的敏感性，有助于更好地反演横波速度结构.

基于背景噪声方法和地震事件获得的面波频散资料，该面波直接成像方法目前已经被广泛应用于不同尺度的三维横波速度结构成像研究中，为认识不同区域的地壳上地幔结构以及地壳浅层精细结构提供了稳定可靠的成像方法，我们将在第3 节中做简要介绍.

2.2 三维方位各向异性横波速度模型反演的面波直接成像方法

三维方位各向异性横波速度模型的直接成像方法（DAzimSurfTomo,Liu et al.,2019）是在三维各向同性横波速度直接成像方法（Fang et al.,2015）的基础上进一步发展得到的.我们在有K个水平格点（k=1,2,...,K）的规则网格的二维球面上对研究区域进行参数化.我们以每个网格点k上的一维横向各向同性分层模型 Θk给出的各向同性相速度作为参考值，这时频率为ω的二维相速度图可以近似表示为：

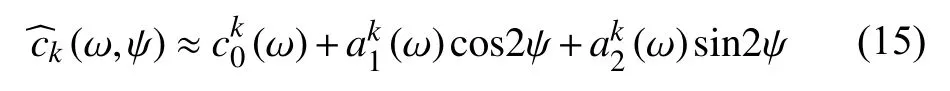
采用双线性插值，我们计算路径上第p段的慢度：

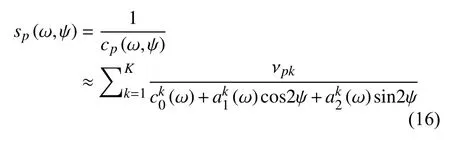
其中 νpk是双线性插值函数系数.第k个格点上的相速度可以由一维横向各向同性分层模型Θk正演计算获得：

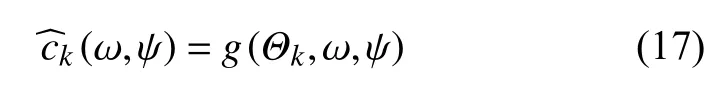
其中g(Θk,ω,ψ)是面波频散的正演计算函数，可以使用传播矩阵方法对具有半无限空间的分层介质进行计算（Haskell,1953;Herrmann,2013），或采用球形介质的自由震荡方法（例如,Dahlen and Tromp,1999;Woodhouse,1988;Yang et al.,2010）.

根据Liu 等（2019），频率为 ω时第i个瑞利面波走时测量可以表示为：

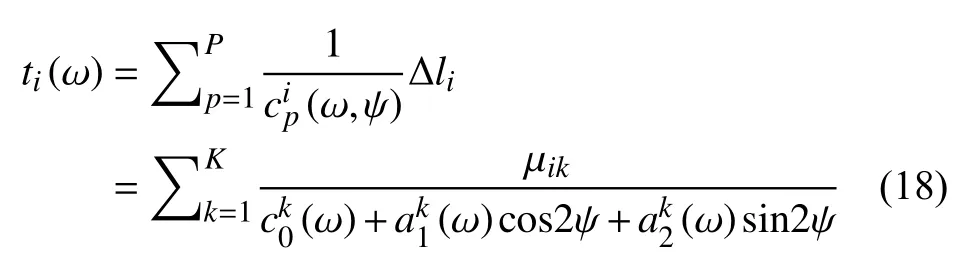
其中 µik是沿着第i个走时数据对应的射线路径上的双线性插值系数.在这里，我们假设方位各向异性相速度变化的幅度通常仅为百分之几，一般远小于各向同性相速度变化.因此，通过快速行进方法（Rawlinson and Sambridge,2004）计算射线路径时仅基于二维各向同性相速度(ω)来计算频率为ω时的射线路径，忽略弱方位各向异性对介质射线路径的影响.

如果我们对方程（18）的面波走时ti进行微扰，并以各向同性相速度(ω)作为参考值，观测值和参考各向同性模型预测值之间的走时残差可近似为：

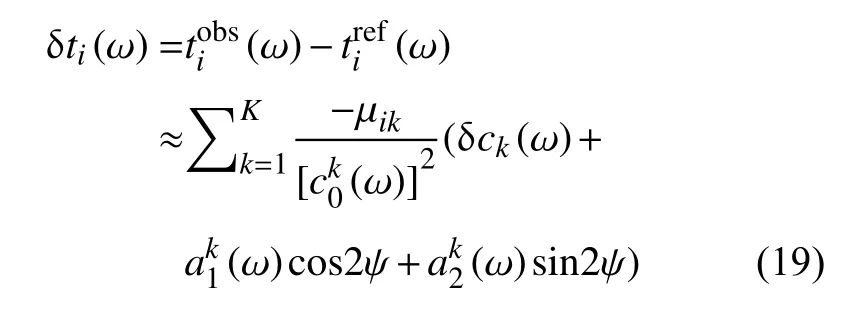
基于Liu 等（2019）的推导，我们最终可以得到：

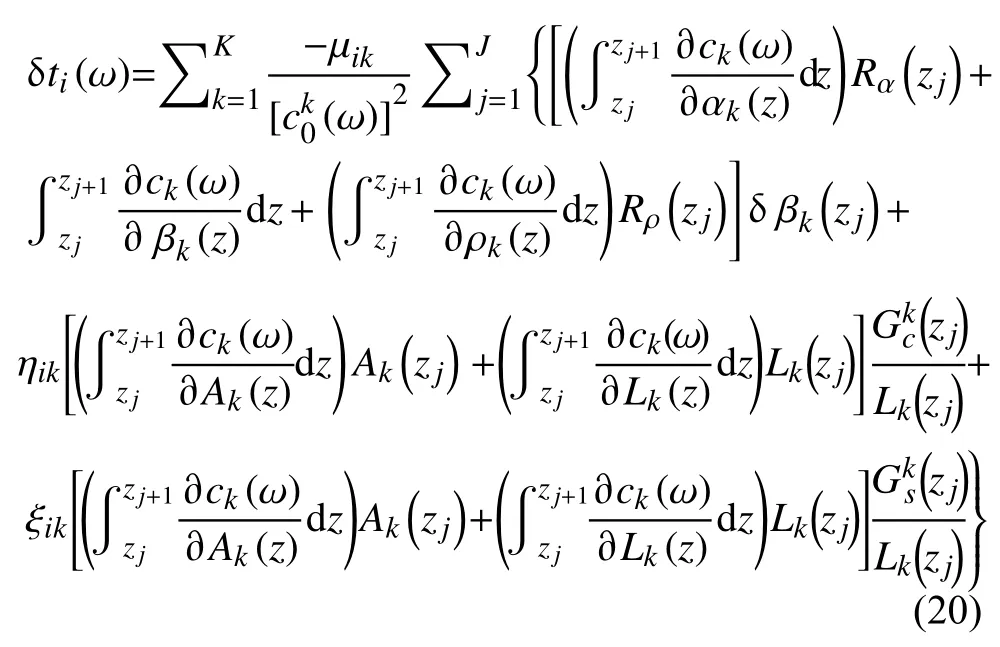
等式（20）可以用d=Gm的矩阵形式来表达，其中d是所有频率、所有路径的瑞利面波走时的残差向量，G是数据敏感核矩阵，模型参数向量m由下式给出：

考虑到模型参数的平滑约束，我们构建的反演方程如下：

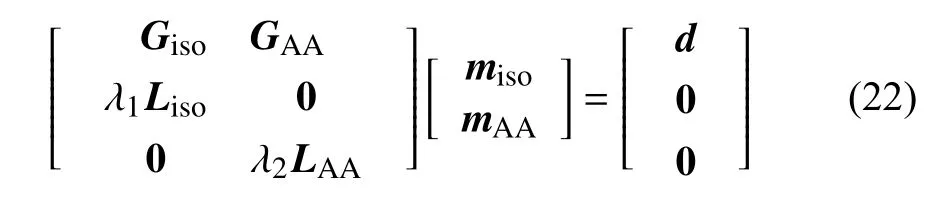
其中Giso和miso对应于公式（20）中第一部分关于对VSV各向同性扰动的敏感核矩阵和横波速度扰动向量，GAA和mAA对应于公式（20）中第二部分关于方位各向异性参数扰动的敏感核矩阵和方位各向异性参数扰动向量，Liso和LAA分别是各向同性和方位各向异性模型参数的粗糙度矩阵，λ1和 λ2是用于平衡数据拟合和模型正则化的权重因子.Liso和LAA通常由Tikhonov 正则化的有限差分算子表示，可以将其选择为一阶或二阶空间导数算子（Aster et al.,2013）.在每次迭代反演中，当各向同性的VSV（即 β）模型迭代更新后，会重新计算二维各向同性相速度分布图以及新的射线路径，再更新各向同性和各向异性参数的敏感核矩阵.通过最后反演得到的模型参数m，我们可以由（9-10）式计算得到横波速度VSV的方位各向异性强度和快波方向.

考虑到各向同性横波速度和方位各向异性参数在反演中可能存在的折衷性（trade-off），我们通常采用两阶段方式进行反演（Liu et al.,2019）：首先基于（13-14）式直接反演三维各向同性的横波速度模型（Fang et al.,2015），然后基于得到的三维各向同性模型作为初始模型再进一步根据（20-22）式同时反演三维各向同性及方位各向异性的横波速度模型.这种两阶段反演方式可以大大减轻各向同性横波速度初始模型的不准确性对方位各向异性反演的影响，一些实际应用例子证实该方法是一种有效和稳定的反演方法.

2.3 三维径向各向异性横波速度模型反演的面波直接成像方法

三维径向各向异性结构的面波直接成像方法（DRadiSurfTomo,Hu et al.,2020）是在各向同性面波直接成像方法（DSurfTomo,Fang et al.,2015）的基础上进一步发展的.该方法可以用来同时反演瑞利波和勒夫波的频散走时数据（TR,TL）来获取平均剪切波速度（VS）和径向各向异性参数ξ=2(VSHVSV)/(VSH+VSV)（Hu et al.,2020）.首先，使用垂直极化剪切波速VSV和无量纲化的径向各向异性参数 γ（定义为γ=VSH/VSV）对模型进行参数化，可以唯一地将通常使用的径向各向异性参数表达为ξ=2(γ-1)/(γ+1)（Huang et al.,2010;Xie et al.,2013）.

当反演参数为VSV和VSH时，根据面波直接反演方法（Fang et al.,2015）的（13）式，基于瑞利波和勒夫波的频散走时数据反演三维VSV和VSH的问题可以表示为：

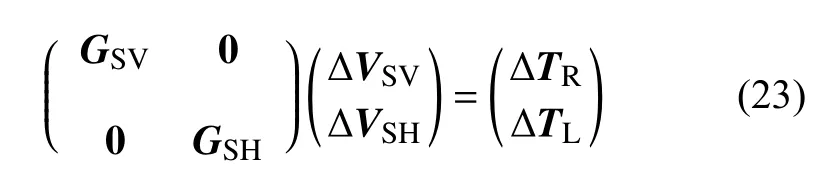
其中 ΔTR和 ΔTL分别是所有路径和所有周期的瑞利波和勒夫波走时的扰动向量;GSV和GSH分别是瑞利波和勒夫波走时相对于横波速度参数VSV和VSH的敏感核矩阵， ΔVSV和 ΔVSH分别是VSV和VSH模型参数的更新向量，在实际反演中我们会分别对 ΔVSV和ΔVSH施加空间平滑约束，通过逐步迭代来获得最终的VSV和VSH模型结果，并计算得到径向各向异性参数ξ.通常勒夫波信号的信噪比相对较低，因此勒夫波频散数据要比瑞利波数据少很多，且勒夫波数据的分辨深度要相对更浅一些（图4）.由于瑞利波和勒夫波射线路径及敏感核的不同，可能会导致VSH反演结果在局部区域不稳定或具有较低的分辨率，因此会导致相应的径向各向异性结果出现不稳定性.

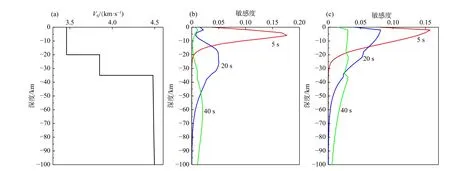
图4 不同周期瑞利波和勒夫波相速度深度敏感核的对比.（a）计算深度敏感核所采用的横波速度模型；（b）5 s、20 s、40 s 周期的瑞利面波相速度的深度敏感核；（c）5 s、20 s、40 s 周期的勒夫面波相速度的深度敏感核Fig.4 The comparison of depth sensitivity kernels of Rayleigh wave and Love wave at different periods.(a) The shear wave velocity model used to compute depth sensitivity kernels;(b) Depth sensitivity kernels of Rayleigh wave phase velocities at periods of 5 s,20 s,and 40 s;(c) Depth sensitivity kernels of Love wave phase velocities at periods of 5 s,20 s,and 40 s

当反演参数转换为VSV和γ 时，基于γ=VSH/VSV，我们可以将ΔVSH表示成：

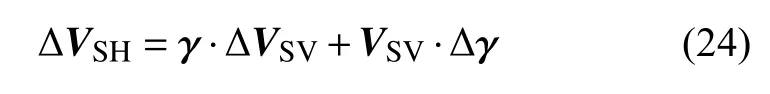
这里γ 和 Δγ分别为向量，算符·表示两个向量元素之间对应相乘，即(A·B)i=AiBi.

将（24）式带入（23）式并进行合并，最后线性化反演问题可表达为：

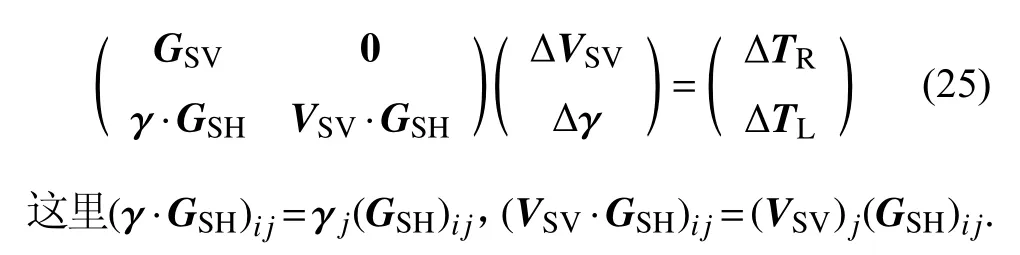
与三维方位各向异性横波速度结构反演类似，我们需要对三维模型参数 ΔVSV和 Δγ分别施加模型平滑正则化项，然后通过迭代求解方法来获得ΔVSV和 Δγ，反演收敛时最终得到VSV和 γ，然后再计算三维平均剪切速度VS=VSV(1+γ)/2和径向各向异性ξ.因为该方法可以直接对无量纲化的径向各向异性参数 γ施加模型正则化平滑，所以可以降低瑞利波和勒夫波路径分布以及深度敏感核差异对反演结果的影响，使得径向各向异性参数的反演结果更加平滑、稳定、可靠.基于理论模型的分辨率测试结果表明，三维径向各向异性模型的直接成像方法可以较单独反演三维VSV和VSH模型，然后再计算得到径向各向异性的方法具有更好的空间分辨率，尤其是在相对深部区域（Hu et al.,2020）.

3 应用实例

在第2 节中我们介绍了基于面波频散走时直接反演三维各向同性横波速度、方位各向异性横波速度以及径向各向异性横波速度模型的成像方法，在本节中我们将展示通过不同区域、不同频带的面波频散走时资料开展不同尺度和不同深度范围的三维横波速度结构直接成像的应用实例.

3.1 三维各向同性横波速度结构直接成像的应用

面波直接成像方法（Fang et al.,2015）已经被广泛应用于不同尺度三维各向同性横波速度结构的反演，包括几百至上千千米的区域尺度的地壳结构（例如,台湾海峡,Chen et al.,2016b;喜马拉雅造山带,Singer et al.,2017;福建—台湾海峡地区,Zhang Y Y et al.,2018;长江中下游成矿带,Luo et al.,2019;郯庐断裂带中南段,Bem et al.,2020;日本中部,Nimiya et al.,2020;青藏高原,Huang et al.,2020），数十千米至数千米的断裂带尺度的上地壳结构（例如,2016 年台湾MW6.4 级梅隆地震震源区,Kuo-Chen et al.,2017;郯庐断裂带肥东段,Gu et al.,2019;龙门山断裂带,Zhang Y T et al.,2020;郯庐断裂带庐江段,Li C et al.,2020;程海断裂带,Yang H F et al.,2020;郯庐断裂带巢湖段,Luo et al.,2021），数千米到数十千米的城市和盆地尺度的地壳浅层结构（例如,台北盆地,Fang et al.,2015;台湾宜兰盆地,Chen et al.,2016a;合肥市区,Li et al.,2016;李玲利等,2020;洛阳盆地,Zhou et al.,2018），以及数千米到数十千米的资源勘探尺度近地表或地壳浅层结构（例如,呼图壁储气库区域,王娟娟等,2018;重庆某页岩气开发水压致裂区,Liu et al.,2018;新疆Cu-Ni 矿集区,Du et al.,2020;辽宁白云金矿区,Li X et al.,2020）.除了采用背景噪声面波数据外，中长周期的地震面波和中短周期的背景噪声面波也联合在一起，用于直接反演地壳上地幔三维横波速度结构，例如福建—台湾海峡地区（Zhang Y Y et al.,2020）和青藏高原东南缘（Zhang Z Q et al.,2020）.

由于地壳浅部介质的横向变化非常大，例如盆地地区的近地表横波速度仅为数百米每秒，但基岩出露的地区近地表横波速度可超过3 km/s，因此在结构复杂区域的地壳浅部结构成像时必须考虑不同周期射线路径的弯曲，否则仅采用大圆路径的面波成像会出现较大的偏差.例如，在台北盆地的地壳浅层噪声面波成像研究中，由于地壳浅层速度结构差异很大，导致射线路径存在较大的弯曲（Fang et al.,2015），且相同台站对、不同周期的面波射线路径会存在明显差异，反映出地下介质随深度也存在不同的变化模式.合肥市区的近地表噪声面波成像研究中（Li et al.,2016），如果假设面波沿大圆路径传播，那么成像结果并不能揭示穿过市区的蜀山断层的位置（图5b），但如果考虑不同周期面波射线路径的弯曲，则可以清晰揭示蜀山断层的位置（图5a）.因此，在面波直接成像方法中考虑不同周期面波射线路径的弯曲效应非常重要，这也是保障结构复杂地区面波各向同性速度结构可靠成像的重要基础，同时也是保障后续各向异性成像结果可靠的重要条件.

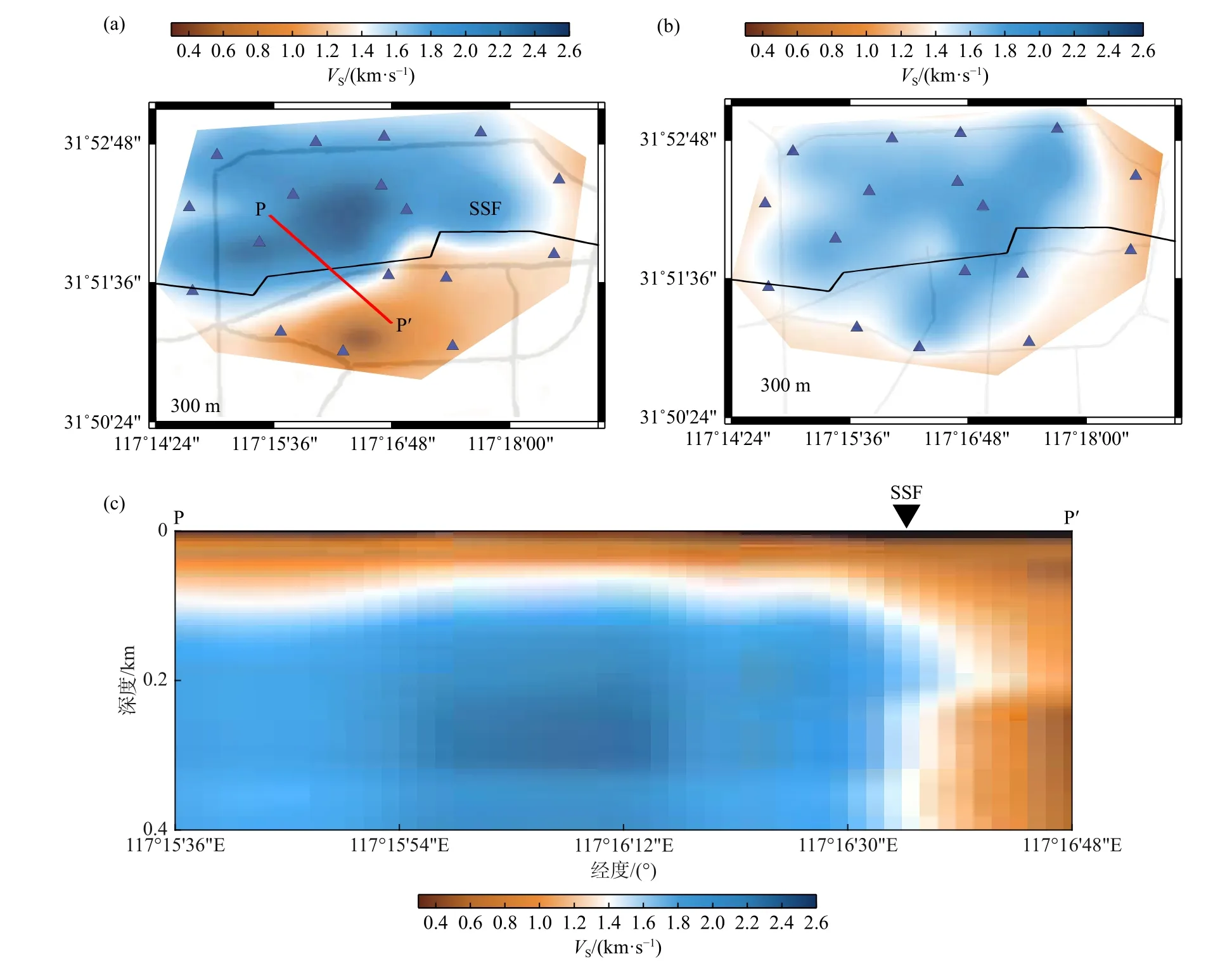
图5 考虑面波射线路径弯曲（a）和大圆路径假设下（b）的300 m 深度处的横波速度反演结果.（a,b）图中三角形表示本研究中使用的地震台站位置，灰线表示合肥市区内的主要道路.黑色实线表示蜀山断层（SSF）位置.红色直线PP'表示横跨断层的一条剖面的位置，其速度剖面如（c）所示.（c）中黑色三角形指示根据速度差异推测的蜀山断层（SSF）的位置（修改自 Li et al.,2016）Fig.5 Shear wave velocity inversion results at the depth of 300 m considering the surface wave ray path bending effect (a) and with the great-circle propagation hypothesis (b).In (a,b) the triangles show the stations used in the study,gray lines show the main roads in the Hefei city,the black line shows the location of the Shushan Fault (SSF),and the red line PP' represents the profile location across the fault,with its velocity profile shown as (c).In (c) the black triangle indicates the location of the Shushan fault (SSF) (modified from Li et al.,2016)

3.2 三维方位各向异性横波速度结构直接成像的应用

基于区域固定和流动宽频带台站的中短周期的背景噪声面波频散数据，三维方位各向异性横波速度结构的面波直接反演方法已经成功应用于数百千米尺度的地壳和上地幔顶部成像研究中，包括云南地区（Liu et al.,2019）、四川盆地及其周缘地区（Zhang Z Q et al.,2022）、渤海湾地区（Li et al.,2022）、郯庐断裂带中南段中部地区（Bem et al.,2022）.这些研究揭示了地壳和上地幔顶部随深度和区域变化的方位各向异性特征，通过与远震和近震横波分裂方法得到的方位各向异性结果对比，更好地揭示了随深度变化的变形模式.例如在云南地区方位各向异性的成像结果（Liu et al.,2019）如图6 所示，地壳方位各向异性的快波方向主要呈现为南北向，主要受南北向的断裂带分布和地壳物质运移的控制；但上地幔顶部的快波方向主要呈近东西向，与远震横波分裂测量的快波方向类似，显示出上地幔物质变形与地壳物质变形的模式显著不同，可能主要受上地幔软流圈物质的东西向流动控制，这与印度板块在缅甸下方的东向俯冲及西向后撤可能密切相关.基于区域固定和流动宽频带台站的中短周期背景噪声面波频散和中长周期地震面波频散的联合成像，Luo 等（2022）获得了郯庐断裂带中南段及邻近区域的地壳上地幔三维方位各向异性的横波速度结构，对认识郯庐断裂带的起源、演化和区域变形机理起到了重要的促进作用.

图6 云南地区三维方位各向异性横波速度结构模型.（a-c）图中的红色短棒显示方位异性的大小和快波方向；图（c）中的蓝色短线显示远震横波分裂测量结果（常利军等，2015），黑色箭头指示板块绝对运动方向（Argus et al.,2011）（修改自Liu et al.,2019）Fig.6 3D azimuthally anisotropic shear wave velocity model in the Yunnan area.In (a-c) the red bars give the amplitude and fast direction of azimuthal anisotropy.The blue bars show the teleseismic shear wave splitting measurements (Chang et al.,2015)and the black arrow indicates the absolute plate motion (Argus et al.,2011) (modified from Liu et al.,2019)

通常固定或流动宽频带台站的间距比较大，一般在数十千米，因此难以提取短周期面波频散数据，所以难以获得地壳浅部或近地表的方位各向异性.而地壳浅部的方位各向异性对于认识区域最大主压应力方向、构造（例如断层）走向分布等具有重要的作用.随着短周期密集台阵的广泛布设，台站之间的间距通常在数千米，甚至达数百米，因此可以有效提取从几赫兹到几秒周期频带的短周期频散曲线，从而可以用于反演地壳浅层的三维方位各向异性，对认识浅部的构造和变形模式具有重要的意义.基于在郯庐断裂带安徽巢湖段和山东潍坊段布设的短周期密集台阵，台站间距约为2～5 km，可以有效提取到0.5 s 周期的短周期面波频散曲线（靳佳琪等,2022;Luo and Yao,2021），最终反演获得了郯庐断裂带不同区段的上地壳精细三维方位各向异性横波速度模型.

图7 展示了郯庐断裂带巢湖段上地壳不同深度的三维方位各向异性横波速度分布图，模型所揭示的异常特征与主要地质单元具有较好的一致性.各向同性结构从西至东整体呈现“交错”模式，即合肥盆地和巢湖东支主要呈现明显的低速异常，这与这些区域自白垩纪以来的松散沉积直接有关，而郯庐断裂带、张八岭隆起以及银屏山地区主要为高速异常，与这些区域广泛出露的岩浆岩、变质岩以及早期沉积岩有关.方位各向异性结构揭示合肥盆地快波方向整体呈现北西—南东方向，反映主要受控于大别造山带节理.与合肥盆地相邻的郯庐断裂带在浅地壳表现为弱方位各向异性，随着深度的增加，在张八岭隆起区域呈现沿断裂带方向（即北北东）的快波异常，可能与郯庐断裂带大规模左旋走滑所产生的构造节理有关.银屏山地区的快波方向与山体走向平行，反映主要受控于中生代华北华南板块汇聚挤压所产生的华南褶皱系.新模型所揭示的方位各向异性速度异常特征为研究郯庐断裂巢湖段浅部地壳变形结构及多期次构造演化活动提供了一个重要的观测窗口.

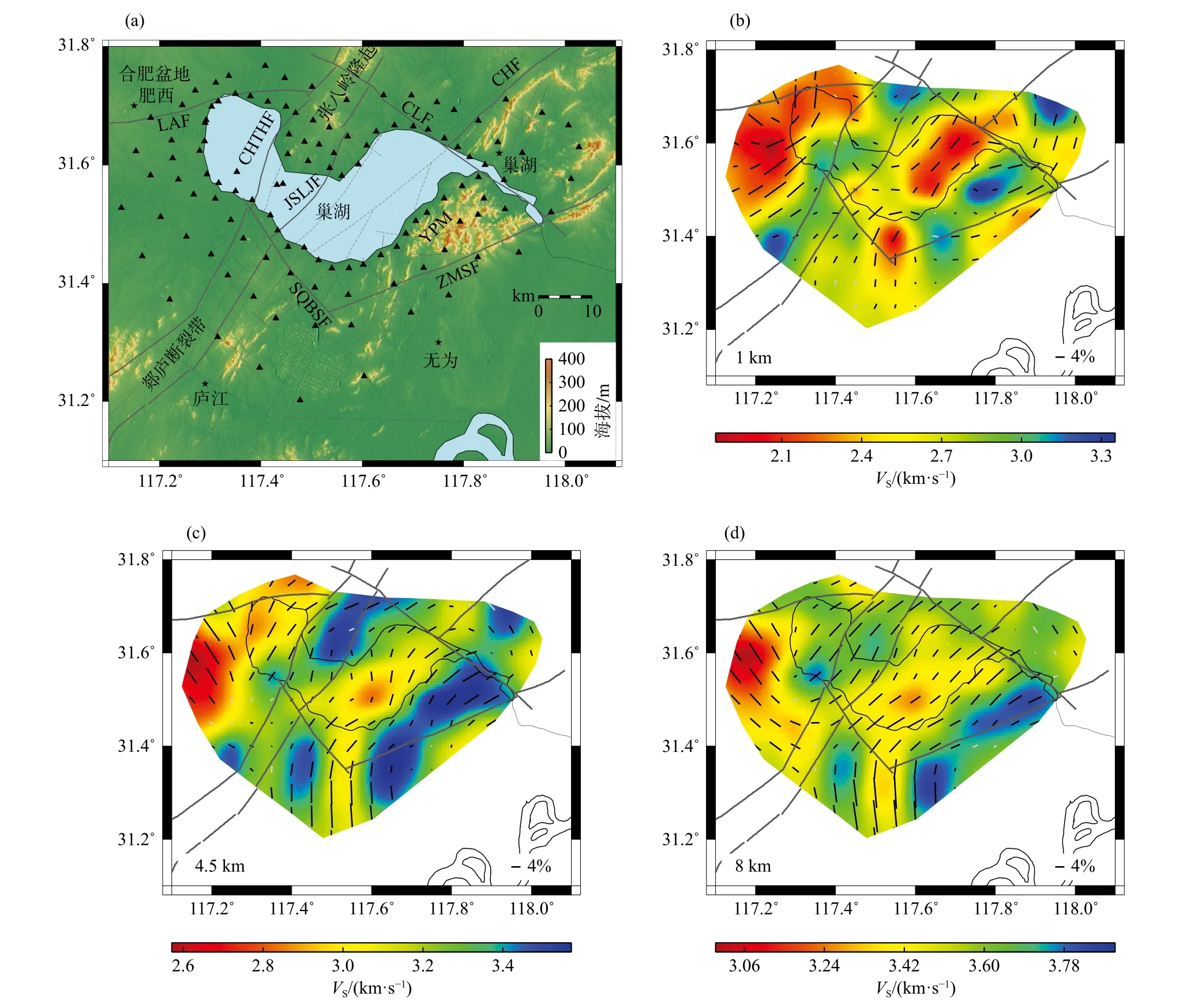
图7 郯庐断裂带巢湖段主要地质单元、地震台站分布和成像结果.（a）研究区域主要地质单元和地震台站分布.其中黑色三角形为地震台站位置，五角星表示主要的城市位置，深灰色实线为主要断裂位置，包括六安断裂（LAF）、巢湖断裂（CLF）、照明山断裂（ZMSF）、滁河断裂（CHF）、嘉山—庐江断裂（JSLJF）、池河—太湖断裂（CHTHF）、盛桥—柏山断裂（SQBSF）.由西至东，主要地质单元包括合肥盆地、张八岭隆起、郯庐断裂带、巢湖、银屏山（YPM）.（b-d）深度分别为1 km、4.5 km 和8 km 深度的各向同性和方位各向异性横波速度分布.其中小短线的长度和方位分别指示方位各向异性的强度和方位角，灰色小短线表示该方位各向异性具有较大误差（修改自Luo and Yao,2021）Fig.7 Distribution of main geological units,seismic stations,and tomographic results in the Chao Lake segment of the Tanlu fault zone.(a) Distribution of major geological units and seismic stations within the study area.The black triangle represents the location of the seismic station.The pentagram represents the location of the main city.The dark gray solid lines indicate the main fault locations,including the LuAn fault (LAF),the Chao Lake fault (CLF),the Zhaomingshan fault (ZMSF),the Chuhe fault (CHF),the Jiashan-Lujiang fault (JSLJF),the Chihe-Taihu fault (CHTHF),and the Shenqiao-Baishan fault (SQBSF).From west to east,the main geological units are the Hefei basin,the Zhangbaling uplift,the Tanlu fault zone,the Chao lake,and the Yinping mountain (YPM).(b-d) Slices of isotropic and azimuthally anisotropic shear wave velocity at depths of 1 km,4.5 km,and 8 km,respectively.The length and azimuth of the short line indicate the strength and azimuth of the anisotropy,respectively.The gray short line indicates that the anisotropy has a large error (modified from Luo and Yao,2021)

3.3 三维径向各向异性横波速度结构直接成像的应用

基于固定台站和布设的流动宽频带台站，三维径向各向异性横波速度结构的直接成像方法已经成功地应用于青藏高原东构造结南迦巴瓦地区（Hu et al.,2020）、小江断裂带及邻区（Yang Y et al.,2020）以及福建和台湾海峡地区（Zhang Y Y et al.,2022），获得了不同研究区域地壳和上地幔顶部高分辨率的三维径向各向异性横波速度结构模型，对认识区域地壳构造变形特征起到了重要的作用.

例如，在喜马拉雅东构造结区域，基于流动宽频带地震数据提取得到了5～40 s 的面波相速度频散数据（Hu et al.,2020）.由于水平分量的噪声互相关数据的信噪比要低于垂直分量的噪声互相关数据，因此最终获得的勒夫波相速度频散走时数据仅约为瑞利波相速度频散走时数据的一半.利用这些面波频散数据直接反演方得到了该区域地壳的三维横波速度以及径向各向异性模型（图8），检测板测试表明该模型的横向分辨率在1.5°左右.

结果显示，该区域横波速度和径向各向异性结构随深度存在明显的变化.在5 km 深度附近，南迦巴瓦峰附近显示为低速且负各向异性（VSV＞VSH），该负各向异性结构从南迦巴瓦峰向东沿着东嘉犁断裂分布.相反，边坝—洛隆断裂显示为高速正各向异性.在25 km 深度附近，该研究区域整体显示为正各向异性.然而，在该深度的速度模型上，沿着东经95°，研究区域被分为东西两个部分，呈现西低东高的特征.在35 km 深度附近，该区域可以大致分为A、B、C 三部分（见图8e 和8f）.其中，A 区域为低速正各向异性，B 区域为高速正各向异性，C 区域为低速负各向异性.结合前人在该区域的地震及其它地球物理研究结果，新模型表明：（1）浅层5 km 附近负径向各向异性结构与较强地震活动性，以及较强应力积累有较好的空间对应关系；（2）中地壳东经95°附近可能存在强度较大的结构，阻断了中下地壳软弱物质自西向东的运移；（3）班公—怒江缝合带以北下地壳（C 区域）的负各向异性可能与印度板块和亚欧板块的挤压碰撞有关.

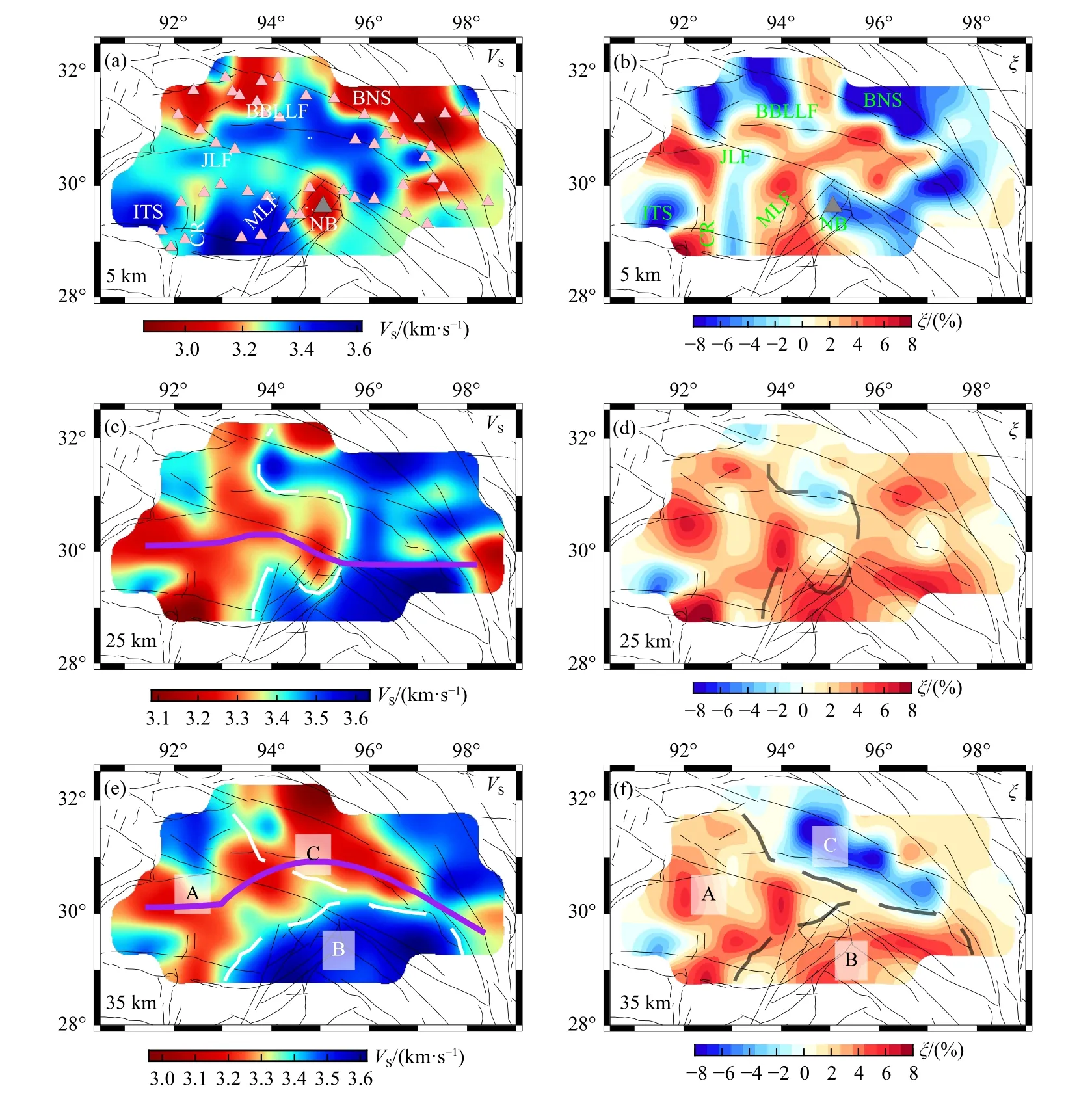
图8 喜马拉雅东构造结5 km、25 km 和35 km 深度的平均横波速度结构Vs（a,c,e）及其相对应深度的径向各向异性结构ξ（b,d,f）.白线和灰线代表划分的不同子区域间的边界.（a）中灰色三角为南迦巴瓦峰的位置，粉色三角为台站位置；（c）和（e）中的紫线代表25 km 和35 km 深度地壳中带状软弱物质的位置.（a）和（b）中英文缩写为：BNS：班公—怒江缝合带；ITS：印度—雅鲁藏布江缝合带；JLF：嘉犁断裂；BB-LLF：边坝—洛龙断裂；CR：Comei 裂谷；MLF：米林断裂；MTF：墨脱断裂；NB：南迦巴瓦（修改自 Hu et al.,2020）Fig.8 Average shear wave velocity VS (a,c,e) and corresponding radial anisotropy ξ (b,d,f) around the eastern Himalayan syntaxis shown at depths of 5 km,25 km,and 35 km,respectively.White and gray dashed lines denote the boundaries for different subregions.Pink triangles in (a) denote the stations used in this study.The gray triangle in (a) denotes the location of Namche Barwa peak.Purple lines in (c) and (e) denote the proposed channelized weak zones at depths of 25 km and 35 km,respectively.Abbreviations in (a) and (b) are as follows: BNS,Bangong-Nujiang Suture;ITS,Indus-Tsangpo Suture;JLF,Jiali Fault;BB-LLF,Bianba-Luolong Fault;CR,Comei Rift;MLF,Mainling Fault;MTF,Motuo Fault;NB,Namche Barwa (modified from Hu et al.,2020)

目前基于短周期密集台阵的水平分量（切向）噪声互相关函数提取勒夫波频散曲线并进一步反演三维VSH结构，以及联合瑞利波频散数据反演三维径向各向异性结构的研究还非常少.一是因为水平分量的噪声互相关函数通常具有较低的信噪比，另外一个重要的原因是在复杂地壳浅部情况下，沿着台站对大圆路径方向旋转得到的切向分量噪声互相关函数有可能还包含了瑞利面波的成分，主要是因为复杂的浅部结构会导致面波传播远偏离大圆路径，使得简单按照大圆路径传播假设旋转得到的切向分量互相关函数（Lin et al.,2009）既包含勒夫波也包含瑞利波.一个可能的矫正方法是利用垂直分量互相关函数的瑞利波和径向分量互相关函数的瑞利波完全相同这一性质，先通过旋转水平分量的互相关函数得到真正反映瑞利波真实传播路径的径向互相关函数（与垂向互相关函数相同；胡亚洲，2021），然后再旋转获得切向分量互相关函数以及更为可靠的勒夫波，从而为后续地壳浅部的三维径向各向异性结构成像提供更为可靠的数据基础.

4 讨论与展望

4.1 面波直接成像方法的频散数据和模型参数设置问题

在背景噪声面波频散提取时，通常要求台站间距离大于2～3 倍波长，以避免噪声互相关函数零时刻附近的信号（例如远场体波）对面波信号的干扰.例如，对间距为百千米的台站对，通常我们可以提取到～15 s 周期的面波频散，可以反演中地壳深度的结构.但百千米及以上间距的台站对难以提取到很短周期（例如1～2 s 或更高频带）的面波频散，主要是由于短周期或高频面波的衰减和散射较强所导致的.随着台站间距的逐渐减小，我们能提取到的面波频散的最长周期越来越小，高频频散数据也越来越丰富，即越来越反映地壳浅层速度结构.

通常而言，中长周期（例如10 s 周期及以上）的面波频散提取相对比较简单，因为拟提取的频散曲线通常与参考频散曲线具有较好的相似性，一般不会出现短周期相速度频散提取时出现的周期跳跃（cycle skipping）问题.需要注意的是，随着周期变长（例如超过30 s 周期），群速度提取的误差会远高于相速度提取的误差（Bensen et al.,2008）.因此，对于尺度在数百千米甚至数千千米的区域台阵噪声面波成像，我们通常仅使用相速度频散数据，而不使用群速度频散数据.

对于密集短周期台阵，通常台阵布设的尺度在数千米到数十千米，由于仪器频带宽度的限制，大部分短周期地震仪很难提取超过10 s 的面波频散，很多间距仅为千米的台站对仅能提取频率为几赫兹的高频面波频散.由于双台高频面波相速度频散曲线提取存在较为严重的周期跳跃问题，在结构非常复杂的地壳浅部区域，面波相速度可能从数百米每秒变为数千米每秒，因此辅助频散提取的参考相速度频散曲线往往与实际观测频散存在很大的偏差，所以双台短周期或高频面波相速度频散曲线的拾取经常会存在很大的误差.但群速度频散时频图像在短周期相对比较简单，通过时频分析方法可以有效自动提取群速度频散曲线，其误差通常小于相速度误差.因此，对于小尺度台阵，当区域结构过于复杂，相速度频散曲线难以提取的时候，我们通常先提取群速度频散曲线，然后基于群速度频散数据先反演获得区域的三维速度结构模型，然后再基于三维模型正演计算台站对之间的相速度频散，以之作为参考频散再进一步提取更为可靠的相速度频散，以避免短周期相速度频散提取的周期跳跃问题.在一些短周期背景噪声成像研究中，有的仅使用群速度频散（例如,Zhou et al.,2018），有的仅使用相速度频散（例如,Fang et al.,2015;Gu et al.,2019;Luo and Yao,2021），有的则是相速度频散和群速度频散联合一起反演三维速度模型（例如,Chen et al.,2016a;Li et al.,2016）.

为了避免相速度或群速度频散在拾取过程中可能存在的较大误差，例如由于周期跳跃、信噪比不高、其他信号干扰所造成的问题，对于密集布设的台阵，我们通常采用路径束分析（path cluster analysis）的方法（Zhang Y Y et al.,2018）.该方法要求相似路径的台站对具有相似的频散曲线，通过统计分析的方法来剔除路径相似但频散出现异常的频散点甚至整条频散曲线，从而进一步保障面波直接成像方法中频散数据的可靠性.

基于面波频散的物理属性、频散资料提取的频带范围以及很多不同尺度台阵的实际噪声成像分辨率结果，我们通常可以有效反演的横波速度结构的最深深度一般小于1/4～1/6 的最长台站间距.在采用面波直接成像方法进行三维横波速度结构反演时，我们设置的反演最深深度通常是最长周期面波波长，但可靠的反演结果通常在1/2 波长深度以内.由于周期越短面波的深度敏感核越窄，即浅部深度分辨率越高，所以在短周期面波资料丰富时，我们通常在浅部设置更密的深度方向网格点；随着深度的逐渐增加，垂直方向设置的网格间距也逐渐增大，这样可以更好地提升浅部结构的分辨率，同时又不至于使得深部分辨率不足时而导致反演系统不稳定的问题.上述这些基本的认识和实际经验有助于我们更好地进行面波直接成像的模型参数设置，使得反演系统的稳定性和分辨率达到较好的平衡.

4.2 基于面波有限频走时和波形反演的三维速度结构成像

目前提出的面波三维直接成像方法基于面波射线理论，所提取的面波频散走时仅反映从源到台站之间的射线路径上的结构信息.很多研究表明，面波具有显著的有限频效应（Nishida,2011;Spetzler et al.,2002;Yoshizawa and Kennett,2005），面波走时不仅对面波射线路径上的结构敏感，还对射线路径之外较宽的区域的结构敏感.一些面波两步法成像的第一步即是开展了基于有限频理论的二维相速度分布反演（例如,Ritzwoller et al.,2002;Yoshizawa and Kennett,2004;Zhao et al.,2020），但二维敏感核的计算是基于一维均匀层状模型的，因此不同周期的面波都是沿着大圆路径传播，这对于反演全球尺度或较大区域尺度的地壳上地幔结构总体而言是合适的.但对于结构复杂的地壳浅部，速度结构不仅存在强烈的横向变化，也存在很大的垂向变化，这会导致短周期或高频面波路径会强烈的弯曲.不同周期面波的敏感深度也不同，很可能会出现同一个源和台站之间不同周期的面波传播路径也存在较大的差异.如果在考虑面波传播走时的有限频效应时不考虑面波传播的弯曲效应，很可能导致走时异常计算存在一定的误差.因此，一些研究在计算面波走时的二维敏感核时也同时考虑面波传播的非大圆路径效应（Lin and Ritzwoller,2010;Russell and Gaherty,2021）.

李成（2019）基于三维谱元法的波场模拟计算面波波场，并通过不同理论（射线理论，有限频理论但假设面波沿大圆路径传播，有限频理论但考虑面波射线路径弯曲）计算得到的台站处面波的走时异常，并与波形互相关方法得到的走时异常进行对比，发现同时考虑有限频理论和面波射线路径弯曲时具有最好的走时异常计算结果.基于这一分析，李成（2019）进一步提出了考虑面波有限频效应和射线路径弯曲效应的面波走时三维敏感核函数（图9）计算方法以及面波三维直接成像方法，并初步应用于台北盆地地区.相比于不考虑有限频效应的面波直接成像方法（Fang et al.,2015），新方法反演得到的地壳浅部的速度异常更强.该方法可以进一步提升面波走时三维直接成像方法在复杂地壳浅层结构成像的精度，相比于三维波形成像具有更高的计算效率，同时也可以结合体波走时的三维敏感核，开展面波与体波走时联合的三维成像.

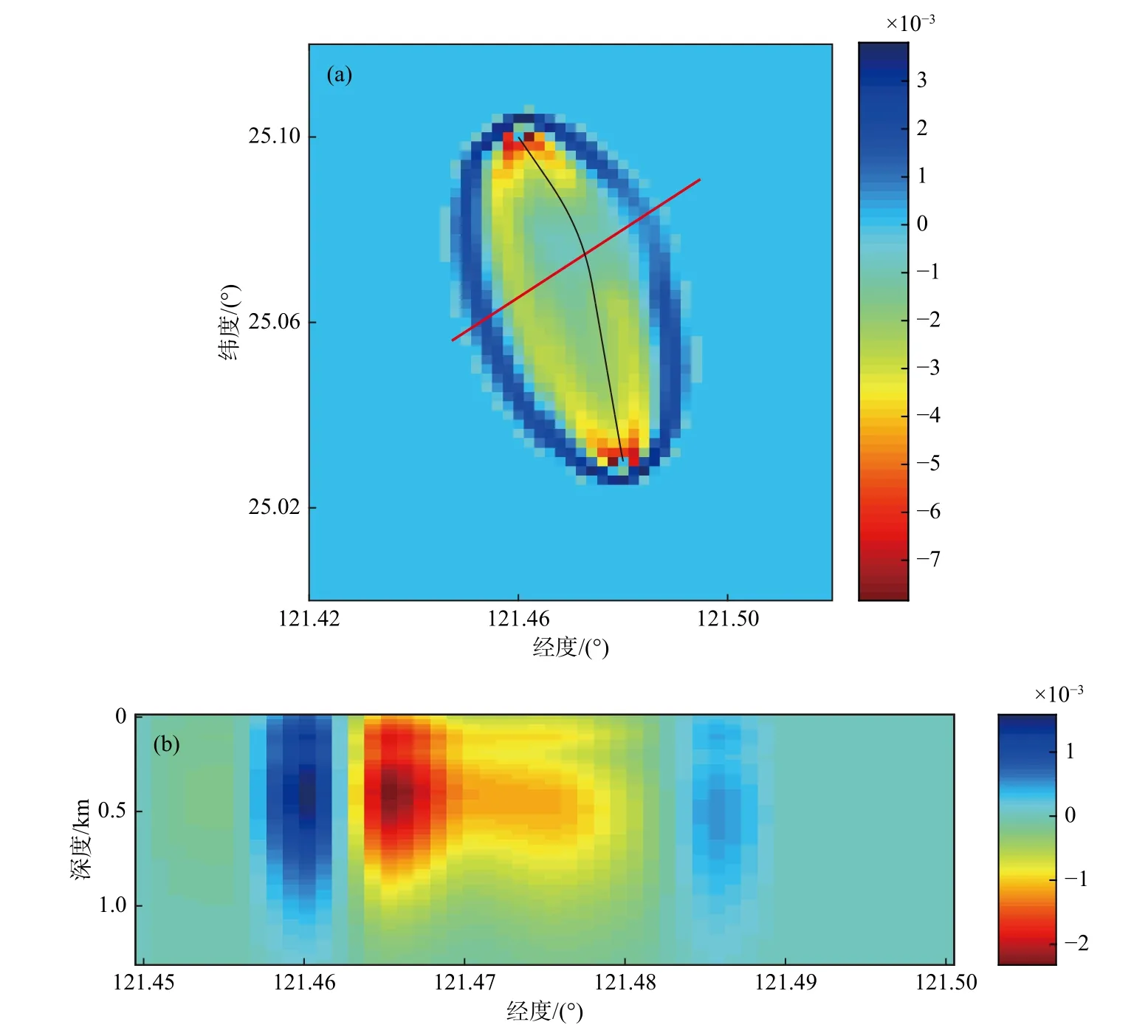
图9 台北盆地两个台站间0.8 s 周期瑞利面波走时的三维敏感核函数.（a）显示了0.4 km 深度处的三维敏感核的水平剖面，黑色实线表示射线路径.（b）显示了三维敏感核的一条纵剖面，位置如（a）中红色实线所示（修改自李成，2019）Fig.9 The 3D sensitivity kernel of the 0.8 s period Rayleigh wave travel-time between two stations in the Taipei Basin.(a) Shows the horizontal cross-section of the 3D sensitivity kernel at 0.4 km depth with the black curve representing the ray path.(b) Shows the vertical cross-section of the 3D sensitivity kernel with its location given as the red line in (a) (modified from Li,2019)

基于面波走时的三维直接成像方法（Fang et al.,2015;Hu et al.,2020;李成,2019;Liu et al.,2019）还并不能考虑更为复杂的波场效应，例如多路径效应.为了更好地利用波形信息，近来一些研究还计算了背景噪声面波的三维敏感核（例如,Tromp et al.,2010），并直接开展基于背景噪声面波波形数据的三维伴随方法成像（adjoint tomography）或全波形成像，虽然计算量远高于基于走时的面波成像方法，但可以获得区域更高精度的各向同性三维横波速度结构模型（例如,Chen et al.,2014,川滇地区;Gao and Shen,2014,美国Cascadia 地区）.最近，通过多分量背景噪声面波波形的三维伴随方法波形成像，Wang 等（2020）反演获得了美国南加州地区三维径向各向异性的横波速度结构模型.目前很多区域开展了线性密集台阵的观测，为了显著降低三维全波形成像的计算量，Groos 等（2017）给出了基于线性台阵高频面波数据的二维全波形成像的完整流程.Zhang C 等（2018）在此基础上进一步提出了线性台阵背景噪声面波伴随方法的波形成像，并成功应用于华北克拉通地区的宽频带线性台阵数据，获得了台阵下方更为可靠的地壳和上地幔顶部二维横波速度结构模型.

目前国际上基于背景噪声面波数据开展全波形成像的工作也越来越多，但针对短周期或高频背景噪声面波数据开展的全波形成像工作还非常少，可能与短周期背景噪声面波波形的复杂性，以及反演需要较好的三维初始模型有一定的关系.此外，背景噪声面波全波形成像中如何考虑噪声源分布的影响也是目前国际上重要的研究方向.考虑到面波全波形成像通常需要较好的三维或二维初始模型，以避免反演陷入局部极小值，以及加速反演的收敛，因此可以考虑先采用基于面波走时的成像方法获得较好的初始模型，然后再开展全波形成像.

4.3 基于频散走时数据和其他数据联合的三维直接成像

基于面波频散走时数据的面波直接成像方法可以有效地获得三维各向同性和各向异性的横波速度结构模型，由于面波频散对纵波速度、密度等参数敏感性较弱，所以目前面波直接成像方法还难以反演除横波速度之外的其他结构参数信息.由于面波直接成像方法构建了从面波走时到三维横波速度结构的正演方程，非常类似于三维体波走时成像的正演方程，因此Fang 等（2016）在三维面波直接成像（Fang et al.,2015）的基础上，进一步提出了体波走时和面波频散走时直接反演三维纵波速度和横波速度结构的联合成像算法，并将该方法成功应用于美国南加州地区以及美国大陆（Golos et al.,2018）.为了获得更为稳定的反演结果，该算法除了施加纵波速度及横波速度模型参数的空间平滑之外，还增加了纵横波速比的物理约束.为了考虑地形起伏对不同网格点下方的面波频散计算的影响，Liu 等（2021）还进一步改进了模型网格参数化的方法，可以考虑地形起伏对面波频散计算的影响.新方法成功应用于我国川滇地区，构建了川滇地区首个三维公共速度模型（Liu et al.,2021）.

体波走时和面波频散走时直接反演三维纵波速度和横波速度结构后，可以通过相除的方法进一步计算得到纵横波速比（VP/VS），但在数据覆盖不是很好的区域得到的波速比可能存在较大的误差.为了获得更为可靠的三维波速比结构，Fang 等（2019）进一步提出了体波走时和面波频散走时联合反演三维纵波速度以及三维波速比（VP/VS）结构的新方法.新方法可以直接对三维波速比施加模型平滑，因此可以获得更为稳定可靠的三维波速比结构，类似于面波频散走时直接反演三维径向各向异性参数的方法（Hu et al.,2020）.

不同的地震学或其他地球物理学数据对不同地下结构参数具有不同的敏感性，如何在现有的三维直接成像的框架下联合更多的数据开展精度更高、可靠性更好的三维结构成像是未来需要进一步发展的方向.例如，联合面波频散走时数据和重力异常数据可以更好地直接反演三维横波速度结构（Du et al.,2021）.基于交替迭代的反演策略，吴萍萍等（2020）实现了电阻率和背景噪声面波的三维联合反演方法，联合反演方法可以获得同时满足两种不同类型数据的更为相似的横波速度和电阻率结构模型.

如何在目前面波频散走时和体波走时（仅包括初至体波走时）联合反演的框架下（Fang et al.,2016,2019），进一步联合多震相体波走时数据（包括直达波、反射波等）、瑞利面波Z/H比数据、体波接收函数等数据，建立更为完善的联合地震学反演方法，更好地反演获得地下三维速度、波速比和界面结构模型是今后重要的研究方向，这也为构建更为可靠的区域公共速度模型提供重要的思路.