区域尺度地震体波和面波走时联合成像：进展与展望

方洪健，刘 影，姚华建，张海江

1 中山大学地球科学与工程学院，珠海 519080

2 南方海洋科学与工程广东省实验室（珠海），珠海 519080

3 中国科学技术大学地球和空间科学学院 地震与地球内部物理实验室，合肥 230026

4 安徽蒙城地球物理国家野外科学观测研究站，蒙城 233500

5 中国科学院比较行星学卓越创新中心，合肥 230026

0 引言

通过观测到的天然地震的地震波数据重建地下的三维波速结构，又称为地震层析成像，是地震学研究的最核心的问题之一.基于获得的波速模型可进一步研究区域/全球构造演化、地震灾害评估、断层形态和地震发震构造等.地震层析成像的基础是地震学的正反演理论.目前，由于计算机计算能力的大幅提升，研究者已经可以相对准确地模拟地震波在复杂介质中的传播过程，并且在全球尺度可模拟到较高的频率（如,Bishop et al.,2021;Mohr et al.,2017;Sun et al.,2021;Zhang et al.,2012）.地震学的正问题是相对稳定的.换句话说，在给定地下介质模型以及地震震源模型的情况下，天然地震学研究常用的一些地震震相可以被准确地且唯一地模拟出来.所以，目前对正演问题的研究大多针对于如何提高模拟高频地震波的效率、如何考虑更加切合实际的介质（如模拟多次散射及衰减）以及如何更好地处理边界等.然而，通过观测到的地震数据确定地下的介质模型（地震学反问题）却存在诸多问题，其中最为突出的是反演结果的非唯一性.著名地球物理学家John Claerbout 曾经说过：“Inverse theory is the fine art of dividing by zero (inverting a singular matrix)”（Claerbout,2014）.换言之，地球物理学家如果想要获得可靠的结果，那么就必须处理好除零，或者处理好反演系统零空间的问题.关于如何减小或消除区域尺度地震层析成像中的零空间，即如何改善区域尺度层析成像波速模型，多数研究主要针对以下几个方面.

首先，可以通过在正演过程中引入更好的物理近似以减小反演的零空间.由于效率较高，目前绝大部分的区域及全球尺度的地震层析成像还是基于射线追踪的走时层析成像.射线追踪常用的方法，如伪弯曲法（Um and Thurber,1987）、基于图像的方法（Moser,1991）等，在复杂模型中通常会由于方法的局限性获得不准确的走时及射线信息.考虑到基于射线追踪获得走时及射线路径的局限性，基于快速行进法（Fast Marching Method）直接求解程函方程获得走时场的方法被提出并被应用到地震成像中（de Kool et al.,2006;Lan and Zhang,2011;Rawlinson and Sambridge,2004;White et al.,2020）.该方法求解过程相对于最初的基于有限差分的方法（Vidale,1990）更为稳定.射线路径可通过追踪走时场的梯度获得.该种方法在复杂的介质中也可以获得较为准确的走时场，并且可以扩展到多种震相以及有地形起伏的各向异性介质（如,de Kool et al.,2006;Lan and Zhang,2011）.尽管基于求解程函方程的走时成像方法较基于传统射线追踪的方法有一定的改进，其更为准确的射线路径以及计算的走时可在一定程度上减小反演的零空间，但其仍然是基于地震波波动方程的高频近似，即认为观测到的走时信息只对射线经过区域的地震波波速敏感.这导致基于线性化方法求解反问题时如果模型网格划分较密，那么获得的结果将会由于反演系统的欠定性而存在非唯一性，即反演系统具有较大的零空间.考虑到基于射线的成像方法的局限性，Dahlen 等（2000）和Hung 等（2000）发展了有限频层析成像方法.有限频成像将观测数据从单一走时扩展到不同频率下的走时，并且考虑不同频率的走时对地下结构的敏感度随着频率的变化而变化，即低频走时的敏感度相对高频的走时的敏感度会扩展到较大范围.值得注意的是，基于有限频层析成像方法对传统射线经过区域无敏感度，其敏感核形状与香蕉-甜甜圈（banana-donut）相似.基于有限频层析成像的敏感核不再是一条无限细的射线，即在同样网格化的情况下，其反演系统的灵敏度矩阵相比于传统的走时成像方法更加稠密，具有相对较小的零空间，所以在相同数据覆盖下，有限频层析成像理论上会获得更稳定的结果.此外，有限频成像方法还考虑了地震波的波前愈合现象.Maceira 等（2015）通过两种成像方法的对比发现有限频层析成像对低速异常的成像效果优于传统走时成像方法.基于有限频成像方法，Montelli 等（2004）首次观测到全球地幔柱的分布及形态，尽管当时该方法较传统方法的优势存在一定的争议（van der Hilst and de Hoop,2005;de Hoop and van der Hilst,2005）.最初的有限频成像方法在求解敏感度矩阵时采用了动态射线追踪的方法，其本质上仍属于波动方程的高频近似.Tromp 等（2005）提出了基于波动方程的伴随层析成像方法.该方法通过直接求解波动方程，所引入的近似相对较少，可以较为准确地计算观测数据对地下结构的敏感度.由于需要强大的计算资源支撑，该种方法目前的应用主要在构建区域及全球尺度模型，并且其观测数据主要为相对低频的波形数据（如,Bozdağ et al.,2016;Fichtner et al.,2009;Lei et al.,2020;Tape et al.,2009;Zhu et al.,2012）.

其次，可通过采用更加符合实际的先验信息以及更合理的网格化方案.地震成像中最常用的先验信息主要有两种: 第一种为假设获得的模型是平滑的；第二种为假设获得的模型不能较初始模型有太大差异.在线性化反演中，这两种信息通常可以通过设计合理的矩阵并整合到灵敏度矩阵，从而减小原始灵敏度矩阵的零空间.除了这两种先验信息，其他的先验信息，如假设模型梯度是稀疏的，或者模型在小波域是稀疏的等，也被应用到了地震层析成像中并取得了良好的效果（如,Chiao and Liang,2003;Fang and Zhang,2014;Loris et al.,2007;Simons et al.,2011）.关于模型的网格化，在基于梯度下降的伴随成像中通常使用求解正演方程的网格.由于基于梯度下降的方法收敛性较慢，通常地震层析成像中可利用目标函数极小值处其导数为零这一特征，直接求解线性方程组以加速收敛.然而，在基于求解线性方程组获得模型变化量的线性化反演中，如何网格化模型有着不可忽略的影响.如果网格较为粗糙，那么反演系统的零空间较小，反演比较稳定，但其代价是模型的分辨率较低.反之，如果网格较为精细，则需要较强的先验信息的约束才能获得较为稳定的结果.所以，在通过求解线性方程的反演中，模型所采用的反演网格通常与正则化项是耦合的.实际反演中反演网格的选取目前没有统一的标准，通常的做法是尝试多种网格化以及规则化方案以检验反演模型的可靠性.此外，反演过程中采用多套网格或者采用非规则网格也在区域及全球成像中取得了一定的改善（Fang et al.,2019;Sambridge and Guđmundsson,1998;Tong et al.,2019;White et al.,2021;Zhang and Thurber,2005;Zhou,2003）.

线性化反演中通过引入先验信息的方法可以在一定程度上减小反演系统的零空间，使得反演稳定.但其缺点是所获得的模型对先验信息的依赖性较大，而且获得的模型通常是一个单一的模型，其误差难以估测.鉴于此，Sambridge（1999）提出直接对模型空间采样的非线性反演方法.该种方法不依赖于梯度信息，故不受初始模型选择的影响.更重要的是，该种方法还可以获得模型的不确定度，这对后续模型的使用至关重要.这种思想被应用到了面波成像（Bodin and Sambridge,2009）、面波接收函数数据联合反演（Bodin et al.,2012）、面波数据直接反演（Zhang et al.,2018）等.由于这种基于对模型空间进行采样的方法需要进行大量的正演计算，且当模型空间的维度过高（比如大于1 000）时无法保证在有限的时间对模型空间进行足够的采样，所以该种方法目前只在少数区域有所应用.所幸的是，近期有研究显示通过引入梯度信息的蒙特卡罗以及机器学习的方法可以进一步减小计算量（Earp et al.,2020;Zhang and Curtis,2019,2021;Zhao et al.,2021）.考虑到模型不确定度在解释过程中的重要性，随着计算机计算能力的继续提升，基于该方法的层析成像将会逐渐取代传统的线性化反演.值得注意的是，该种方法没有通过减小零空间来增加获得模型可靠性，而是通过搜索可以拟合数据及符合先验信息的多个模型，最后通过模型的统计学参数，如均值及方差来获得稳定的模型及其不确定度.

最后，由于观测到的地震记录上不同震相通常对地下结构具有不同的灵敏度，所以在观测系统无法改变的情况下，通过整合更多的地震观测信息是减小或者消除反演系统零空间最直接的方法.如上所述，通过拟合观测到的全部波形信息，即全波形反演，来构建地下结构模型是地震层析成像的终极目标.但是，通过近30 年的研究显示，真正意义的全波形反演目前还很难达到.其主要原因有以下几个方面：首先，地震波场模拟比较耗时；其次，波形信息（反演所采用的目标函数）通常与波速结构存在非常强的非线性关系，导致优化过程中如果初始模型选择不合理容易陷入局部极值；波形反演过程中目标函数的选择、地震震源时间函数处理等都会影响到获得结果.此外，由于波形的振幅信息通常会受到很多因素的影响，如地震震源、衰减结构、地震波传播时受结构的影响会出现聚焦以及散焦、场地效应以及地震仪的耦合等，以至于绝大多数波形成像还无法使用波形的绝对振幅信息.所以，目前基于波形的层析成像主要针对单一震相，如初至波、面波等.或者在同时拟合多种震相时只拟合频率较低的波形.相比之下，联合反演同样遵循利用更多地震记录上的信息来构建地下波速结构.其基本思想是将地震记录上的信息拆分成不同震相，如P 波、S 波、面波等.然后对于不同的震相可使用效率较高的正演方法，如求解程函方程.之后将所有震相的数据整合到同一反演系统中，从而达到利用更多波形信息以减小反演系统零空间的目的.

利用不同数据对模型具有不同灵敏度的联合反演的方法在研究大地震断层面滑移分布规律中已有较多应用（如,Cirella et al.,2018;Delouis et al.,2002;Inbal et al.,2017;Koketsu,2016;Konca et al.,2007;Yokota et al.,2011;Yue et al.,2014）.此外，不同种类的数据，如地震数据和大地电磁数据、地震数据和重力数据等，也可以通过结构约束，如交叉梯度，或者将不同物性之间的一些经验关系整合到同一反演系统中来共同约束地下结构（如,Bao et al.,2021;Bennington et al.,2015;Lin and Zhdanov,2019;Maceira and Ammon,2009;Popovici et al.,2017;Roecker et al.,2004;Syracuse et al.,2016;Zhdanov et al.,2012）.对于地震成像方面已有很多综述文章，感兴趣的读者可以参考近期的综述文章，如Liu 和Gu（2012）、Rawlinson 等（2010）、Thurber和Ritsema（2015）等.本文主要针对区域尺度不同震相联合反演获得地壳上地幔三维波速结构的方法，介绍其基本原理以及目前的应用情况，着重介绍其在构建川滇公共速度模型中的应用，最后探讨一些可进一步改善的方案.

1 地震数据联合反演

1.1 区域尺度体波走时层析成像

区域尺度观测到的地震体波（包括直达P、S 波，Pn 波和Sn 波）到时数据可以用于构建区域三维波速模型.在使用单种数据，如P 波数据进行成像时，基于线性化的体波走时层析成像方法通常可以简化成如下方程：

当然，S 波也可以整合到以上方程来同时获得三维的VP和VS波速结构.其线性化的方程如下：

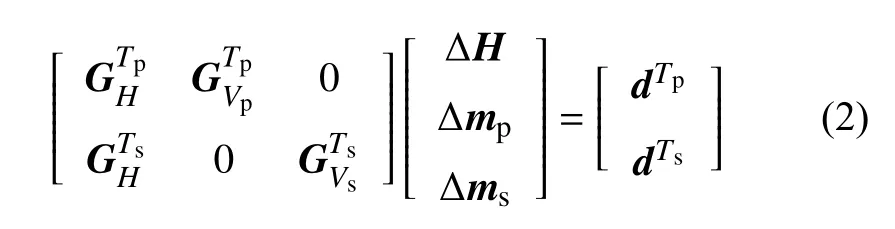
1.2 区域尺度面波层析成像

基于面波频散数据的区域尺度面波成像通常分为两步.首先将测量的不同周期的面波频散数据进行成像获得二维的相速度或者群速度面，然后再通过空间点上反演获得的不同周期相速度或者群速度进行一维反演获得地下的VS结构.最后通过整合不同空间点的一维VS结构便可获得区域的三维VS结构.总的来说，该种成像方法将面波反演分解成两个计算量相对较小的子过程.由于计算量较小，可以对两步法获得的模型进行详细的误差分析来评估模型的不确定度.但是两步法反演也有着一定的不足.比如，如果某些周期频散数据较少，尽管该周期对地下不同深度结构有着不同程度的约束，但由于不能获得稳定的相速度或者群速度面，所以该种数据通常会被舍弃.而面波频散数据的数量在不同周期差异很大是很普遍的.此外，通常在进行两步法成像时并不考虑面波的非大圆路径传播的影响.由于短周期面波主要对地壳结构比较敏感，而地壳结构相比于上地幔结构通常具有较大的横向差异.所以，对于利用噪声数据互相关获得的短周期面波数据在地壳结构复杂区域基于面波大圆路径传播的假设会产生较大误差（李想等,2015;Xia et al.,2018）.考虑到两步法面波成像的不足，Fang 等（2015）发展了基于射线追踪的面波频散数据直接反演的方法.其主要思想是将不同周期面波的深度敏感核和水平方向的敏感核整合到一起以建立从三维VS结构到面波频散数据的方程.直接反演的线性化方程如下：

1.3 体波走时与面波相速度图联合反演

区域尺度地震图上最显著的震相为直达P 波、直达S 波（图1）.由于震级较小或者较深地震面波通常不发育，所以在区域尺度上很少有直接利用区域地震面波进行成像的.近20 年来，通过对噪声数据互相关恢复台站之间格林函数的方法已被广泛应用到不同尺度地壳及上地幔的地震成像中（如,Lin et al.,2007;Shapiro et al.,2005;Yang et al.,2007;Yao et al.,2006）.受噪声源性质的影响，恢复的格林函数中面波的成分占主导（见图1）.在地震走时层析成像中，利用直达P 波和S 波进行成像时在射线分布稀疏以及射线交叉较少区域（通常在浅部）其纵向分辨率较低.利用面波数据进行成像时在浅部具有较高的分辨率，但其纵向分辨率会随着频率的减小而降低.所以，联合地震体波及面波数据进行成像可以利用两种数据对结构敏感度具有互补的特性，降低反演系统的零空间.

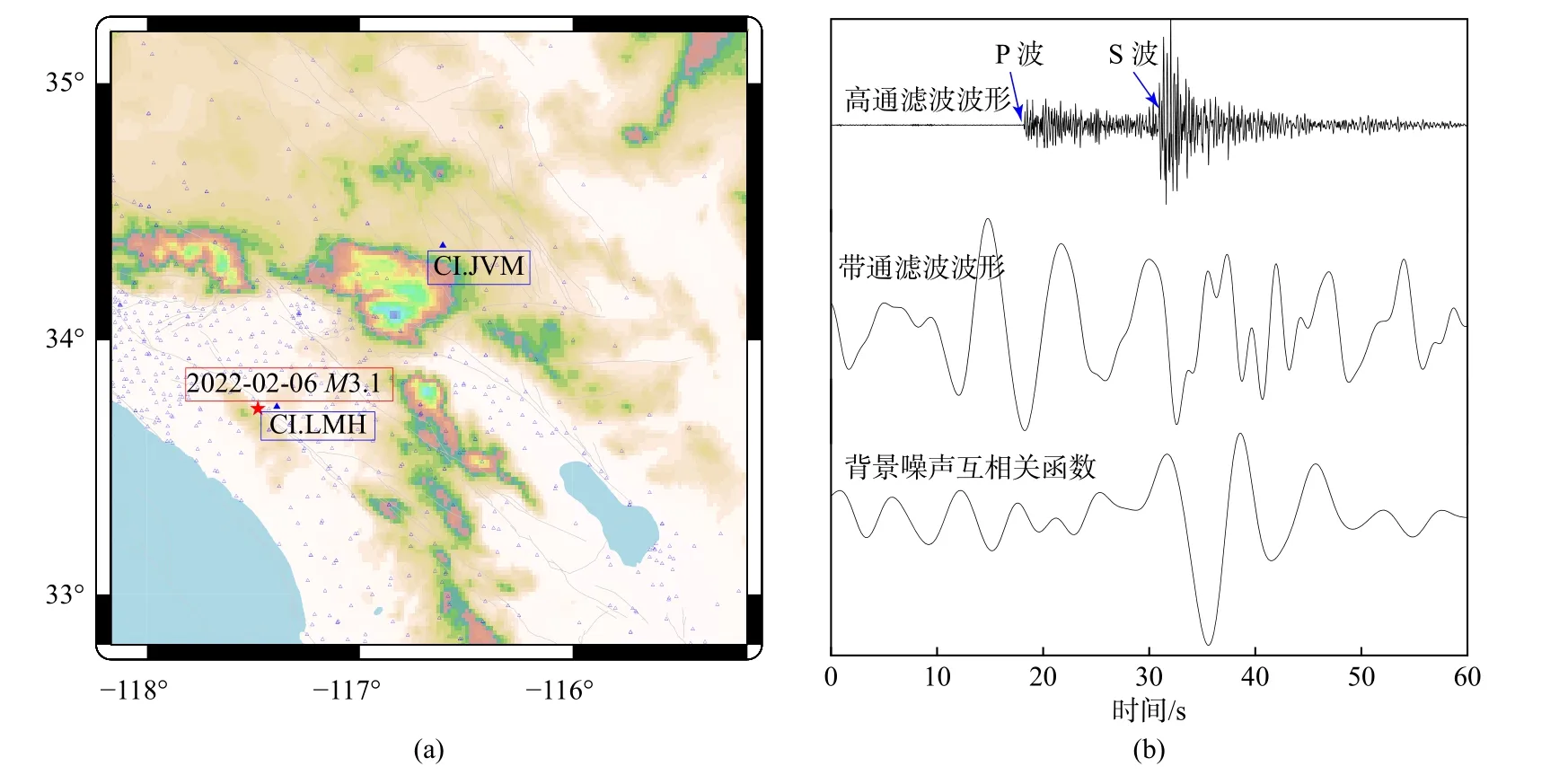
图1 以美国南加州为例的区域尺度观测的地震波形及噪声互相关记录.（a）南加州地区宽频带地震台站分布（蓝色三角形）.（b）2022 年2 月6 日一个震级为3.1 级地震[位置见图（a）红色五角星]在CI.JVM 台站垂直分量[位置见图（a）标注的蓝色三角形]不同频段的波形记录.其中图（b）上波形为1.0 Hz 的高通滤波，其次为带通滤波，频率范围为0.05～0.5 Hz.图（b）下图显示离地震位置较近的台站CI.LMH 及CI.JVM 台站间互相关记录.互相关利用了2022年2 月到3 月一个月的连续记录.由图可知区域尺度上地震P 波和S 波较为明显，但面波不发育.联合反演中的面波数据可由台站间通过对连续记录进行互相关获得.全波形成像受计算资源限制，通常只拟合低频的地震波形，而区域尺度低频波形常常具有较低的信噪比，故需对用来反演的波形进行严格的质量控制Fig.1 The seismic waveforms and ambient noise cross-correlation function of two stations in Southern California.(a) The blue triangles show the distribution of broadband seismic stations in Southern California.(b) The vertical components of a magnitude 3.1 earthquake (marked as red star in the left panel) at station CI.JVM (marked as blue filled triangle in the left panel) at different frequencies.The right top waveform is high pass filtered at 1 Hz and the right middle waveform is band pass filtered at 0.05～0.5 Hz.The right bottom shows the ambient noise cross-correlation function between station CI.LMH and CI.JVM using one-month continuous records (from February to March 2022).P-wave and S-wave could be easily recognized in the earthquake recording,but surface wave is difficult to identify.For regional-scale joint inversion,the surface wave data can be obtained by ambient noise cross-correlation using continuous records.For full waveform tomography,only low frequencies are used due to the large computational cost.As the signal to noise ratio of low frequency waveform at region scale is relatively low,strict quality control should be applied on the waveforms when doing full waveform tomography

当原始频散数据无法获得时，体波走时成像可通过整合公开的不同周期面波的相/群速度进行联合反演，以共同约束地下结构（Zhang et al.,2014）.其求解方程如下：

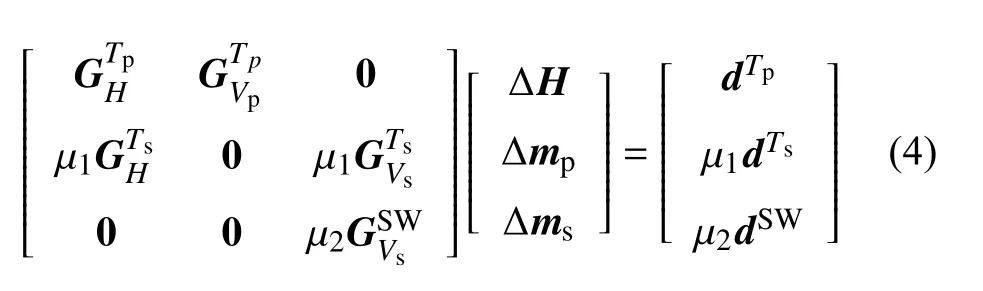
1.4 体波走时与面波频散数据联合反演

考虑到传统联合体波走时数据和面波相速度面数据反演方法的局限性，如面波数据与体波数据类型不一致而导致很难选择两种数据的权重以及短周期面波复杂传播路径的问题，Fang 等（2016）发展了区域体波和通过噪声数据互相关获得的面波数据的联合反演，该方法可综合利用体波和面波数据对地下不同区域结构的敏感性，获得一个可以同时拟合不同数据的统一的、自洽的模型.这种方法本质上与West 等（2004）提出的联合反演方法相似，即基于面波直接反演的方法同时反演体波和面波数据.具体来说，可通过将面波的深度敏感核整合到求解相/群速度面时的二维敏感核，以建立三维波速结构与面波频散数据之间的关系，这样面波数据的反演思路就可等同于体波数据的反演，进而可将面波反演与体波反演整合到同一反演系统以达到联合反演的目的.该种反演思想被广泛用于区域尺度地壳及上地幔的成像（如,Feng and An,2010;Nunn et al.,2014;Obrebski et al.,2011），所用的体波及面波数据皆来自天然地震.值得指出的是，新的联合反演方法利用基于射线追踪的短周期面波直接反演的方法（Fang et al.,2015），所以该方法考虑了短周期面波在复杂结构中并非沿着大圆路径传播的问题.由于面波直接反演方程与体波反演方程的相似性，可直接将二者整合到同一反演系统.新的联合反演需求解的线性方程为：

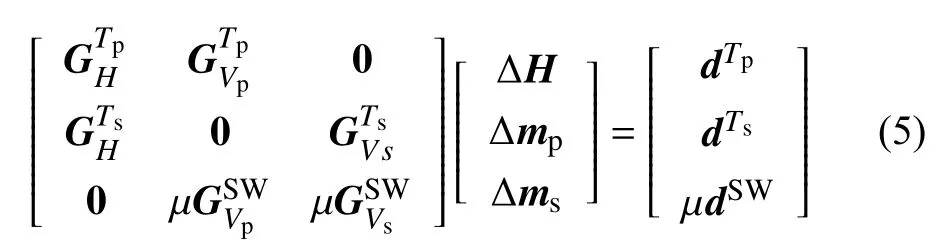
合成数据测试结果证明了两种数据对地下结构具有互补的灵敏度并且获得的模型优于单独反演的结果（图2）.其在美国南加州地区的应用所获得的模型能够很好地刻画断层带结构及盆地结构等.而且，获得的模型较南加州地区参考模型能更好地拟合地震观测记录，证明了联合反演方法具有较大的应用潜力.该种方法目前已被用于构建川滇区域公共速度模型（Liu et al.,2021）、阿拉斯加地区模型（Nayak et al.,2020）、北美板块三维波速模型（Golos et al.,2018）等.Liu 等（2021）在构建川滇区域参考模型时还考虑了地形起伏对获得模型的影响，这为后续带有强烈地形起伏的利用体波和短周期面波联合成像更广泛的应用奠定了基础.

图2 体波和面波数据联合反演合成数据测试.（a）输入模型；（b）由联合反演获得的模型；（c）体波数据单独反演的模型；（d）面波数据单独反演的模型.左列显示VS，右列显示VP.由图可知联合反演相比于体波数据单独反演在浅部有较大改善，较面波单独反演对VP 以及深部模型改善较大，并且异常的整体幅度与输入模型更为接近，可更好地约束VP/VS 模型（修改自Fang et al.,2016）Fig.2 Synthetic test of joint inversion of body-and surface-wave data.(a) Input model;(b) Recovered model from joint inversion;(c) Separate inversion using body wave only;(d) Separate inversion using surface wave only are shown from the top to bottom.The left and right column show the VS and VP model,respectively.The resolution at shallow depths is improved in the joint inversion compared to separate inversioin using the body wave only.Besides,the joint inversion improves VP model significantly compared to separate inversion surface wave only.The better resolved anomaly amplitude in the joint inversion leads to more realiable VP/VS model (modified from Fang et al.,2016)

1.5 川滇地区的应用

本节主要以构建川滇地区公共模型为例讨论体波面波联合反演方法的应用.首先概括川滇地区公共速度模型构建的必要性以及联合反演模型的特征.之后详细介绍联合反演中所用的体波和面波数据、模型构建、分辨率分析以及模型验证.

印度板块与欧亚板块碰撞导致了青藏高原的隆升以及高原内部和川滇地区大地震的频繁发生，高原演化模型至今存在诸多争议.一个较为准确的高分辨率三维岩石圈波速模型是进一步认识该区域的构造演化及进行地震灾害评估分析的基础.因此，川滇地区公共壳幔模型的构建是目前一大研究热点.现已有研究利用不同的数据资料（如体波到时、面波频散、面波振幅比、远震P 波接收函数等），通过不同的地震层析成像方法（如地震体波走时层析成像、面波层析成像、接收函数、联合反演等），获得了川滇地区地壳及上地幔的结构（波速模型、Moho 面起伏模型等）.目前，大部分模型是基于单一数据反演所构建的，因此通常只能拟合单一类型的数据，各个模型之间的一致性还有待验证.此外，受数据和方法的限制，川滇地区已有三维速度模型的横向分辨率最高可达50～100 km，垂向分辨率约为10～20 km.如前文所述，相对于单一数据反演，地震体波及面波联合反演可以在拟合两种数据的同时，基于两种数据对于介质速度结构具有互补的敏感性以获得更为可靠的、分辨率更高的三维VP及VS模型.

Liu 等（2021）从中国地震台网中心收集了2008 年10 月至2016 年9 月期间川滇地区230 个固定台站的体波到时数据，共计约20 万地震事件、94 万P 波到时、92 万S 波到时.具体数据质量控制和筛选过程如下：（1）保留初至到时，去除明显不符合时距曲线的数据；（2）仅保留被10 个以上台站同时记录到的地震事件；（3）在此基础之上，考虑到川滇地区地震事件分布极不均匀，将整个区域划分为多个体积相等的长方体，每个长方体仅随机选择一个地震事件进行保留.最终保留了约33 000个地震事件、39 万P 波初至到时、37 万S 波初至到时，并构建了约138 万地震对双差走时数据.对于面波数据，Liu 等（2021）收集了约8 100 条瑞利面波相速度频散数据，频带范围为5～50 s.该数据包括从124 个固定台站提取的6 910 条瑞利面波相速度频散（Yang et al.,2019），从35 个临时台阵提取的544 条瑞利面波相速度频散（Yao et al.,2010），以及从16 个临时台站和云南地区49 个固定台站提取的640 条瑞利面波相速度频散（Qiao et al.,2018）.

由于目前联合反演方法还是基于线性化反演思路，因此初始模型的选择会在一定程度上影响反演的结果，过于偏离真实模型的初始模型会导致反演陷入局部极值，获得误差较大的反演结果.本研究以Yang 等（2019）通过联合反演获得的川滇地区三维VS模型为基础，通过地壳VP与VS经验公式Brocher（2005）转换获得三维VP模型，并应用高斯平滑，构建了一个包含先验信息且较为平滑的三维VP及VS模型.在体波及面波联合反演程序中，Fang 等（2016）将模型设置成了相对于平均海平面的水平层状等间隔网格.本研究在反演过程中采用了多尺度网格反演策略，首先将水平方向的网格设置为0.5°×0.5°进行反演，然后以此结果作为初始模型，再进行水平网格为0.25°×0.25°的反演.考虑到川滇地区的实际地形，将深度方向的网格点范围设置为-5～100 km，网格间隔随深度增加而增加（50 km 以上为5 km 间隔，50～70 km 为10 km 间隔，70～100 km 深度为30 km 间隔）.由于川滇地区高程起伏较大，在进行体波走时和面波频散正演及敏感度矩阵计算时都考虑了实际的高程信息.其中，对于体波走时，在正演和敏感度矩阵计算时均考虑台站高程.对于面波频散走时，在正演频散和计算深度敏感核时，考虑该地理位置的真实高程进行计算.为避免联合反演被单一数据所主导，在反演过程中，每次迭代前通过估算体波和面波数据的误差，来确定两种数据的权重.最终，经过11 次迭代，体波走时的均方根残差从0.93 s 下降至0.43 s，面波频散走时的均方根残差从4.16 s 下降至2.06 s.

基于川滇地区丰富的地震体波及背景噪声面波数据，利用体波及面波联合反演方法构建了川滇地区公共波速模型1.0 版本.该版本包括了地壳及上地幔顶部（深度70 km 以上）的三维VP及VS模型（图3、4）.在地壳浅部（5 km 左右），地壳结构比较复杂.四川盆地显示相对较低的VS，沿着龙门山断裂西北显示条带状的高速异常.四川盆地内部的速度异常有着横向不均匀性，川西、川东之间存在较强的速度结构差异.在20 km 左右，以龙门山断层为界，VP及VS模型在青藏高原和四川盆地分别为大范围低速和高速异常.低VP及VS异常位于龙门山—丽江—小金河断裂带以西以及小江断裂带附近.值得注意的是，这两个低速异常并不相通，而是被位于安宁河断裂带、则木河断裂带下方的高速异常所隔开.该高速异常的位置与峨眉山大火成岩省内带相对应.因此，Liu 等（2021）认为位于西侧的大范围中下地壳低速异常可能反映了青藏高原物质的东南向挤出，而位于东侧的小范围中下地壳低速异常很可能并非来源于青藏高原.张智奇等（2020）结合上地幔三维VS分布，认为小江断裂带附近的小范围低速异常可能是由于长英质地壳在较高温下发生塑性变形甚至部分熔融而形成的.在下地壳至上地幔顶部深度（40 km 以下），VP及VS的高低速异常分布与Moho 面深度相对应.从地震重定位结果来看，大部分地震发生于高速异常内部或高低速异常边界，3 级以上地震基本位于大型断裂带上.

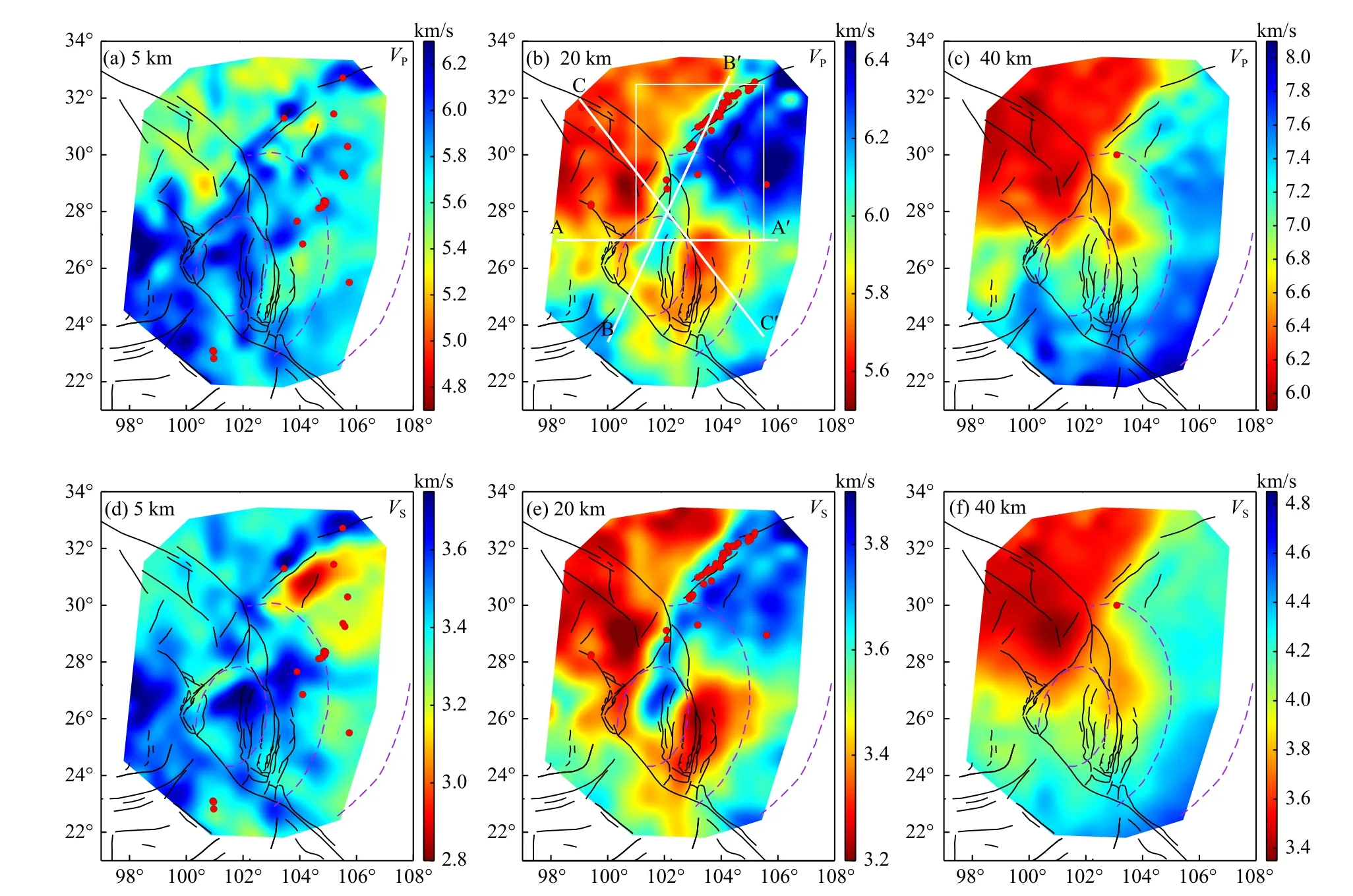
图3 川滇公共速度模型（1.0 版本）在不同深度（相对于平均海平面）的VP 及VS 分布.其中，黑色实线为区域主要断层分布，紫色虚线为峨眉山大火成岩省的内、中、外带，红色圆点为4.0 级以上地震的重定位结果（修改自Liu et al.,2021）Fig.3 The community velocity model (V1.0) of southwest China at different depths (the depth sea level is 0 km).Solid black lines represent major faults in this region.Purple dashed lines mark the inner,intermediate,and outer boundary of the Emeishan large igneous province.The relocated events with magnitude larger than 4.0 are shown in red circles (modified from Liu et al.,2021)

为了验证模型的可靠性，本研究进行了棋盘测试，以评价在模型当前观测系统及网格设置下的模型分辨能力.为更好地模拟真实射线路径，本研究选择了最终反演所获得的三维VP及VS模型作为初始模型，在水平和垂直方向加以±5%的扰动.考虑到数据在不同深度的分辨率能力不同，设置了随深度而变化的速度异常尺度：中上地壳的速度异常横向和垂向尺度约为50 km 和10 km，中下地壳的速度异常横向和垂向尺度约为75 km 和20 km.分辨率测试结果显示，在路径覆盖较好的区域，测试结果显示基本能够恢复所设置的速度异常，模型的横向分辨率为50～75 km，纵向分辨率为10～20 km，相比于该区域已有模型具有较高的分辨率.为定量分析模型的不确定性，本研究通过随机抽取数据重复反演来进行自举法分析.结果显示，在绝大多数区域，VP及VS模型的标准差在0.05 km/s 以内，自举法分析获得的平均模型与反演所获得的模型基本一致.尽管自举法分析所重复的反演次数有限，并不能真正地统计分析模型的不确定性，但这仍在一定程度上说明了通过当前数据和方法反演获得的模型是较为稳定可靠的.

为进一步验证模型的可靠性，该研究将所获得的模型与川滇地区已有的三个模型进行对比，分别是：Xin 等（2019）通过体波走时单独反演获得的中国大陆岩石圈参考模型1.0 版本，Shen 等（2016）通过面波频散单独反演获得的中国大陆地壳及上地幔三维VS模型，Yang 等（2019）通过面波频散、ZH 振幅比和接收函数联合反演获得的川滇地区地壳及上地幔顶部三维VS模型.另外，选取了三种不同类型的数据（面波单点频散、ZH 振幅比以及气枪P 波到时），利用上述几种模型分别进行正演，对比不同模型对于不同数据的拟合情况.结果显示，不同模型之间存在整体一致性，但仍存在一定的差异，尤其是在浅部较为明显.除了使用接收函数数据的Yang 等（2019）模型，其他模型在Moho 面处都是较为平滑的.相比于Shen 等（2016）和Xin等（2019），Liu 等（2021）和Yang 等（2019）对于面波频散数据的拟合较好.Liu 等（2021）和Xin 等（2019）对于ZH 振幅比的拟合基本处于同一水平，优于Shen 等（2016），但次于Yang 等（2019）.值得注意的是，这里用于正演的面波单点频散数据和ZH 振幅比数据均来自于Yang 等（2019）.Liu 等（2021）和Xin 等（2019）对于气枪P 波到时数据的拟合程度基本一致.这说明通过体波及面波联合反演所获得的模型（Liu et al.,2021）对未参与反演的体波或者面波数据的拟合并不比通过单一数据反演所获得的模型差（Shen et al.,2016;Xin et al.,2019）.

此外，我们还对比了利用本文介绍的两种不同体波面波联合反演方法获得的模型的差异.图4g-4l展示了Gao 等（2017）通过联合体波走时和面波相速度图的反演所获得的青藏高原东南缘（101°E～105.5°E,27°N～32.5°N）三维VP及VS模型，其使用的是Zhang 等（2014）所发展的体波走时与面波相速度图联合反演方法.其VP模型横向分辨率约为50 km，VS模型横向分辨率在中上地壳可达50 km.对比发现，两个模型在中上地壳（30 km）以上整体具有较好一致性，如龙门山断裂带下方在地壳浅部的低速异常，丽江—小金河断裂带以西的中下地壳低速异常等.但由于所使用的数据与方法不同，两个模型仍然具有一定的差异，尤其在下地壳深度.例如，在Gao 等（2017）的VP及VS模型中，Moho 面深度附近的速度起伏较大，且VP及VS模型差异较大，对反映下地壳流的低速异常成像效果也有待提高.

图4 川滇公共速度模型（1.0 版本）在不同纵切面的VP 及VS（a-f），以及Gao 等（2017）在相应纵切面的VP 及VS（gl）.剖面位置如图3b 所示，红色十字为4.0 级以上地震的重定位结果.断层位置以箭头标识：CHF：程海断裂；LZJF：绿汁江断裂；XJF：小江断裂带；RRF：红河断裂带；DLSF：大凉山断裂；LMSF：龙门山断裂带；LXJF：丽江—小金河断裂带Fig.4 Vertical profiles of the community velocity model (V1.0) of southwest China (a-f) and the model from Gao et al.(2017) (g-l).The locations of profiles are shown in Fig.3b.The plus signs are relocated earthquakes with magnitude larger than 4.0.The faults are marked by arrows and labeled: CHF: Chenghai fault;LZJF: Lvzhijiang fault;XJF: Xiaojiang fault;RRF: Red River fault;DLSF: Daliangshan fault;LMSF: Longmenshan fault;LXJF: Lijiang-Xiaojinhe fault

综上所述，相较于单一数据反演，通过体波走时和面波频散走时联合反演不仅可以同时获得三维VP及VS模型，并且所获得的三维VP及VS模型具有更高的分辨率和可靠性.此外，联合反演所获得的模型也能较好地同时拟合两种类型的数据.通过更可靠的VP及VS模型可以获得泊松比模型，可为定量刻画中下地壳物质组分及熔融程度提供新的约束.

2 展 望

随着地震记录数据的指数级增长以及计算机计算能力的提升，地震层析成像将会是人类认识地球内部过程不可或缺的工具.而如何更充分地挖掘利用地震记录获得高精度的地下结构将会是层析成像方法研究的核心内容.联合地震记录上不同震相走时信息的反演具有原理的简单以及容易实现的优点，且其反演相比于全波形反演受初始模型影响相对较小.此外，由于走时信息通常是从高频的地震图上获得，而波形反演所利用的波形信息以及有限频层析成像中的到时信息一般通过相对低频的波形获得，在区域尺度成像中目前还没有关于二者成像精度直接的对比.在南加州区域，基于走时信息的反演在某些区域获得的波速模型对观测数据的拟合甚至优于基于波形反演获得的模型（Fang et al.,2016）.特别是基于机器学习算法的发展来识别地震以及进行震相的拾取（Mousavi et al.,2020;Zhu and Beroza,2019）可以获得大量的走时信息，这将推进基于走时信息的联合反演的广泛应用.所以，全波形反演在区域尺度成像中仍然不能取代基于不同震相走时信息联合反演.二者的结合还可能获得更高分辨率地下结构，如通过联合反演获得的模型还可作为波形反演的初始模型来进一步拟合更高频的信息，这样便可以继续改善所获得的模型.类似的思想其实已经在利用远震数据进行上地幔成像时有所体现，如Rawlinson 和Fishwick（2012）发现利用面波成像获得的模型作为初始模型可以保留数据约束较小区域的大尺度特征.此外，目前区域尺度的利用t*数据的衰减成像以及利用横波分裂的各向异性成像均依赖于获得的各向同性模型，所以联合反演获得的模型还能为其他模型的建立提供基础.今后的联合反演方法的进一步发展及应用可能体现在以下几个方面.

2.1 反演模型误差估计

基于线性化反演的零空间可通过设置恰当的反演网格来减少或消除，如设置随着射线覆盖而变化的网格（Chiao and Liang,2003;White et al.,2021;Zhou,2003），但是由于观测数据总是会有误差，这种误差将会传递到所获得的模型.如何刻画模型的误差/不确定度对后续结果解释至关重要.由于观测数据的误差通常很难估计，基于对模型空间采样的非线性反演方法，如基于马尔科夫链的蒙特卡罗方法可通过假设误差分布遵循一定的物理模型，而同时获得多个可以拟合数据的模型以及误差分布的模型，进而刻画获得模型的不确定度（Galetti et al.,2017;Zhang and Curtis,2020）.另外，在地震活动性较高的区域，反演模型可通过对数据进行采样，如某些地震在空间上相邻，那么反演时便可通过随机选取其中某一地震进行多次反演，进而估算由数据误差引起的模型的不确定度（Fang et al.,2019）.

2.2 降低不同种类参数反演中的耦合

目前基于走时信息获得各向异性成像的方法已被广泛应用于区域各向异性结构成像（如,Eberhart-Phillips and Mark Henderson,2004;Huang et al.,2011;Wang and Zhao,2008），其公式推导主要基于弱各向异性模型（Backus,1965;Smith and Dahlen,1973）.即各向异性反演过程中假设波速随方位的变化可以分解为各向同性的波速加上一些随方位变化的改正量，然后同时反演各向同性波速以及控制改正量的参数，进而同时获得各向同性波速以及各向异性结构.不难看出，各向同性参数与各向异性参数间有着强烈的耦合，即在各向异性强的地区如果只做各向同性结构成像，那么各向异性分量可能会投射到各向同性模型中，造成假象.反之，如果在各向异性较弱的区域反演考虑各向异性，由于反演参数过多，那么数据观测误差就有可能传播到获得的各向异性模型.而这些假象通常很难通过合成数据测试进行评估，所以目前还没有比较好的方法消除其影响.

可幸的是，目前获得的各向异性模型与区域地质在不同程度上有着相关性，而且通过不同方法，如面波方位各向异性、接收函数方位各向异性、横波分裂等获得的各向异性存在可比性.所以，尽管各向异性模型误差难以评估，研究者仍然可以通过模型研究区域构造演化等问题.虽然线性化反演时各向同性和各向异性之间的耦合难以消除，但反演过程中通常可以采用一些约束以减小模型参数之间的依赖.如通常可以先反演各向同性模型，待模型收敛后再继续反演各向异性模型（Liu et al.,2019），测试结果表明这种分步式的方法要优于同时反演所有参数.实际上，这种思路已被用于一些高精度地震层析成像中，如基于双差走时层析成像便是首先拟合绝对到时信息，然后逐渐加入双差走时信息，以逐步改善震源区波速结构以及地震的位置，虽然其实现方式是通过对不同种类的数据予以不同权重，然后在反演过程中随着迭代次数的改变而改变权重的大小（Zhang and Thurber,2003）.所以，通过联合反演获得的各向同性模型可以为之后各向异性反演提供一个更好的初始模型，以最大限度减小模型参数之间的耦合，从而获得更加可靠的各向异性模型.当然，各向异性参数也可以作为模型参数加入到联合反演系统，以同时获得各向同性模型和各向异性模型，其耦合也可通过对不同数据在不同的迭代阶段设置不同的权重而得到控制.此外，各向异性和各向同性参数的耦合程度还取决于射线路径的分布.Huang 等（2015）通过详细的理论测试发现，在射线路径分布单一时，各向异性结构与各向同性速度异常会产生严重耦合.只有当射线路径覆盖足够，且方位角分布均匀时，才能获得较为可靠的各向异性模型（Huang et al.,2015;黄周传,2022）.

2.3 联合反演框架

区域尺度的层析成像中，目前应用较多的联合反演有基于面波及接收函数的联合反演（如,Bao et al.,2015;Chen and Niu,2016;Gama et al.,2021;Guo et al.,2015;Julià et al.,2000;Obrebski et al.,2015;Shen et al.,2013;Ward et al.,2014）、基于体波及面波走时的联合反演（Eberhart-Phillips and Fry,2017;Fang et al.,2016;Guo et al.,2018;Obrebski et al.,2011,2012;Yang et al.,2021）、远震走时及区域地震波形联合反演（如,Schmid et al.,2008）、远震波形数据及噪声互相关的联合反演（Gao,2016;Wang et al.,2021）以及面波、接收函数及振幅比的联合反演（Berg et al.,2018;Shen and Ritzwoller,2016;Yang et al.,2019）.其中，面波数据振幅比数据对约束近地表波速结构尤为重要，通常可以被整合到面波相速度或者接收函数反演中以同时约束从浅到深的波速结构（如,Chong et al.,2016;Li et al.,2016;Lin et al.,2012）.此外，近期研究表明远震记录中的极化方向数据也能较好地约束地表的P 波及S 波结构（Park and Ishii,2018）.这种数据已被整合到接收函数、面波振幅比数据中以共同约束浅地表结构（Xiao et al.,2021）.实际上，这些从地震记录上提取的信息皆可整合到同一反演系统中，从而获得一个统一的模型.具体来说，除了区域地震及互相关获得的短周期面波数据，远震体波以及长周期面波也可以整合到反演系统以获得上地幔结构.如Chang 等（2010）及Liu 和Zhao（2016）等整合近震、远震S 波走时数据以及瑞利面波相速度数据，构建了从地表到700 km 左右的高精度S 波波速模型，并论证了其相对于单独反演的优越性.接收函数以及振幅比数据可通过单点的信息加入到反演系统，类似体波以及面波二维相/群速度图联合反演方式（Eberhart-Phillips and Fry,2017;Zhang et al.,2014），从而构建一个多种数据共同约束的P 波和S 波波速模型（图5）.

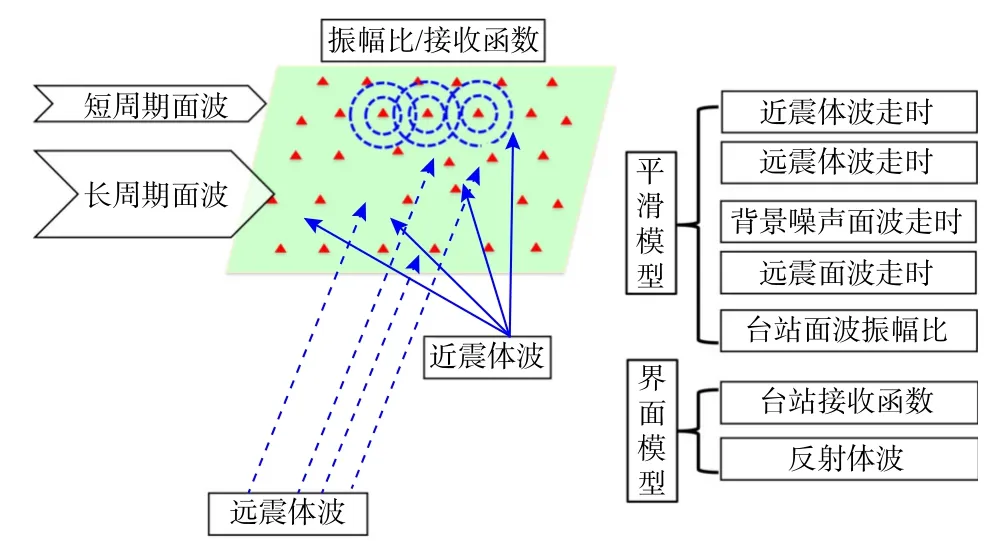
图5 地震学数据联合反演框架Fig.5 The framework of joint inversion with different kinds of seismic data

2.4 定量化解释

层析成像获得的波速模型本身可以服务于其他地震学研究，如通过三维的波速模型可以更好地约束地震的震源机制、大地震的破裂过程，以及通过强地面运动模拟为地震灾害评估提供参考等.在通过模型研究具体科学问题时，目前模型的解释多数只局限于定性的描述（主要是将波速异常对应于岩性、温度、含水量等方面），如低速异常可能代表流体、沉积物、破碎带，高速异常通常和基底、火成岩以及稳定地块联系起来，当然这在一定程度上受控于反演本身的不确定性以及多解性.随着越来越多的观测数据的加入、更符合实际的物理模拟以及更准确的不确定度的刻画，层析成像获得的模型的定量化解释将会成为一种新的趋势，比如俯冲带低速异常可以和含水量联系起来（Cai et al.,2018），火山地区低速异常可以反推出岩浆的熔融程度以及岩浆囊的体积（Li et al.,2016），或者在贝叶斯的框架下直接由地球物理数据定量约束地下的岩性温度等（Afonso et al.,2013），结合其他学科观测以及动力学等模拟，层析成像波速模型将会在定量刻画地球内部过程和地震灾害评估中发挥重要作用.