基于能力导向的工科高等数学教学——以方向导数与梯度为例

张京良

（中国海洋大学 数学科学学院，山东 青岛 266100）

高等数学是工科类专业的一门公共基础必修课，其内容多、学分重和抽象性强，教学效果直接影响到工科专业的人才培养质量。

近几年，工科类专业正在进行两个重要方面的建设，一是工程教育专业认证，二是新工科建设。工程教育专业认证中要求学生具备应用、分析、评价和创造等高阶学习能力[1]；新工科人才培养中要求学生具有较强的创新思维和实践应用能力[2]。工科类专业的发展对作为基础必修课的高等数学教学提出了新要求：教学中应注重能力培养。

传统的高等数学教学多是重视数学知识的讲解，关注数学的抽象性、严密性，强调计算和证明的技巧性，导致学生学习兴趣低、能力提升慢，不适应工科专业发展对数学教学的要求。为强化学生能力培养，我们在教学中补充了生活、工程等方面的应用性案例作为课堂引例，案例的应用性提高了学生的学习兴趣，案例的分析、解决过程培养了学生的知识应用能力和创造性思维能力。实践表明，案例教学法不但能更好地推动知识教学目标的实现，而且能有效促进能力教学目标的达成。

下面以方向导数与梯度为例给出详细的能力导向的教学设计。

一、教材内容和学情分析

（一）教材内容分析

方向导数与梯度在教材[3-4]中被安排在偏导数的应用部分，意图是想说明用偏导数可以计算出方向导数与梯度，所以教材中直接引入了方向导数与梯度的概念，然后给出方向导数与梯度的计算公式。教材中没有说明这两个概念自身的应用场景，造成了概念引入突兀、直观理解欠缺。如果按照教材内容直接进行传统讲授，学生学完本节知识后对方向导数与梯度的计算能够掌握，但对它的本质并不理解，进而难以提升他们对数学的学习兴趣，更谈不上知识应用能力和创造性思维的培养。换句话说，就是教学目标中的知识目标能够达到，但能力目标就很难达到了。为此，对该节知识的讲授有必要进行推敲研究[5-7]，做好能力导向的教学设计工作。

（二）学情分析

传统的高等数学教学往往以教师为中心、以知识讲授为目的，学生习惯于被动听讲，学习兴趣与学习主动性不够，导致学生知识掌握不牢固、能力培养跟不上。如何以学生为中心，提高学生学习兴趣，重视知识理解、强化能力培养，是高等数学教学面临的挑战。

二、教学策略与教学目标

（一）教学策略

针对高等数学在传统教学中遇到的上述问题，我们的教学策略是：采用能力为导向的教学设计，在教学内容中引入生活、工程和军事等方面的应用性案例，用案例教学法进行教学。一方面，案例的应用性可以提高学生的学习兴趣；另一方面，案例的分析、解决与实验验证过程可以培养学生的知识应用能力和创造性思维能力。

（二）教学目标

为满足中国海洋大学“高素质创新人才”的培养要求和适应工程教育认证与新工科建设的需求，我们优化了本节教学目标，强化了能力培养与价值塑造。

（1）知识目标：记住方向导数与梯度的概念；理解偏导数与方向导数的关系；掌握方向导数与梯度的计算。

（2）能力目标：通过飞机在雷暴区飞行问题与蚂蚁逃跑问题两个案例的分析、解决及实验验证来提高分析问题、解决问题的能力和创造性思维能力；通过方向导数与梯度的计算来提高数值计算能力。

（3）素质目标：通过对极限思想、归纳演绎法和例证法的运用来提高在数学思想、数学方法方面的素养。

（4）价值目标：通过方向导数与梯度在登山与速降、梯田修建、图像处理和洋流预测等方面的应用，提高学习兴趣，树立积极的学习观；通过分组讨论增强团结协作精神。

三、教学内容与教学过程

（一）新课导入

首先，播放电影《中国机长》中飞机在雷暴区飞行片段，导入案例1[8]。

引例1 飞机在雷暴区飞行问题。飞机飞入雷暴区时，可能遭遇雷击，给飞行安全带来很大隐患。这就要求驾驶员制定合理的飞行路线，尽快飞离雷暴区。问飞行员应该按照什么路线飞行才合理?

接着，进行问题分析。事实上，雷暴区的气压低，飞离雷暴区就是尽快从气压低的地方飞到气压高的地方。需要解决两方面问题。

（1）沿某个方向，气压变化度怎么表示？

（2）沿哪个方向，气压变化度最大？

然后导入案例2。

引例2 蚂蚁逃跑问题。设平面上有一铁板，红点表示一热源，铁板上有一蚂蚁。蚂蚁感觉到发烫时就会逃走。问蚂蚁沿什么方向逃跑，才能尽快逃到凉爽区？

再进行问题分析。蚂蚁应该沿着温度下降最快的方向逃跑。需要解决两方面问题。

（1）沿某个方向，温度变化度怎么表示？

（2）沿哪个方向，温度变化度最大？

然后对两个案例进行小结，指出引例1 中的（1）与引例2 中的（1）本质上是本节要学的方向导数；引例1 中的（2）与引例2 中的（2）本质上是第二节课要学的梯度。

（二）方向导数

1.方向导数的定义

先进行引例1 中的问题（1）的解决：以雷暴区中心为原点，建立坐标系。假设发生雷暴时飞机的飞行高度不变，气压函数为z=p（x，y）。任取一方向P0P，设P0（x0，y0），P（x，y），则在P0点处沿P0P 方向的气压变化度为

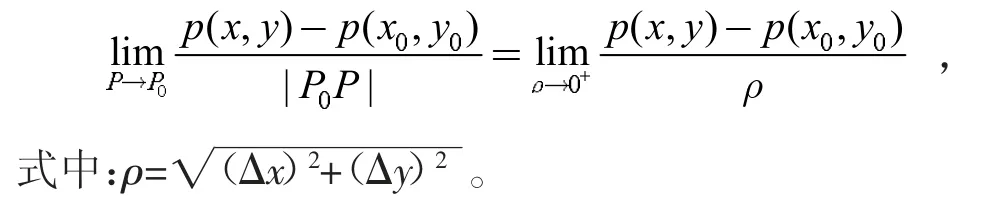
再进行引例2 中问题（1）的解决：建立坐标系，设温度函数为z=T（x，y），任取一方向P0P，设P0（x0，y0），P（x，y）则在P0处沿P0P 方向的温度变化度为

总之，互联网环境下，图书从传统的长形式变迁为长形式与网形式结合的形态，是对当前超文本阅读环境的一种积极适应，也是对长形式图书生命力的极大延伸。读者在原界面与跨界面的不断切换中，实现从阅读到跃读的循环，如此，长形式图书的商业价值与阅读价值同时得以提升，或许这就是图书出版业未来发展的主流趋势。

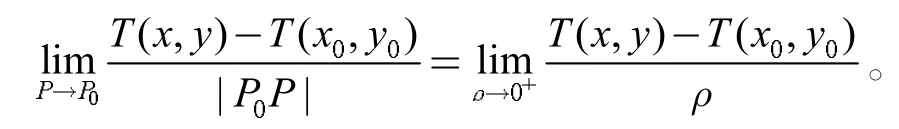
最后对两个问题的共性进行总结：上述是两个不同的问题，发现它们的解决方法相同，最后得到的结果形式相同。类似这样的问题不只有这两个，还有很多，如研究电场时考虑电压沿不同方向的变化、攻山作战时需要研究山坡陡峭度沿不同方向的变化等，这一类问题解决方法相同、最后结果形式类似，故对这一类问题进行概括归纳，总结出其共性，并加以抽象，就得到了一个新的概念，称为方向导数。

定义1：设l 是xoy 平面上以P0（x0，y0）为始点的一条射线，函数z=f（x，y）在点P0（x0，y0）的某一邻域U（P0）内有定义，P（x，y）∈U（P0）为l 上另一点。令如果极限存在，则称此极限为函数f（x，y）在点P0沿方向l 的方向导数，记作

注：此处可进行课程思政教育，解决这一类问题时所用的数学思想——极限思想，给出方向导数定义时采用的数学方法——演绎归纳法，这种数学思想与数学方法以前使用过，如导数的定义、定积分的定义，今后还将继续使用，如重积分的定义、线面积分的定义。

2.方向导数与偏导数的关系

前面已经学过了偏导数，现在介绍方向导数，自然讨论二者的关系。以取l=x 为例，先写出二者的定义

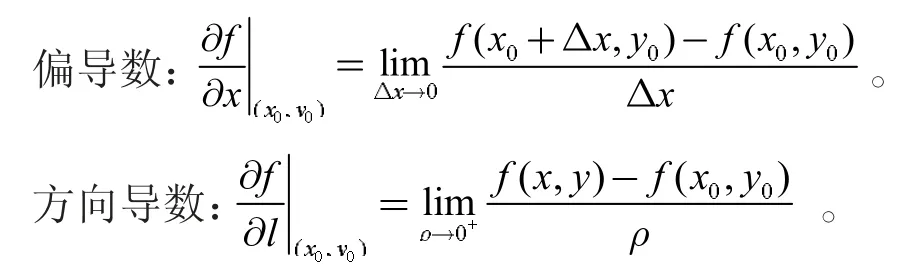
发现，偏导数是双侧极限，方向导数是单侧极限，故方向导数存在，偏导数不一定存在；反之，若偏导数存在，方向导数是否一定存在呢？不一定，用例证法，举例说明。

易求得：函数沿任何方向的方向导数都不存在，但两个偏导数都是0。

此例说明，偏导数存在保证不了方向导数存在，那函数满足什么条件时方向导数才存在呢？启发学生：能否把条件加强一下？前面学习全微分时知道，全微分存在可推出偏导数存在，故此处换为偏微分存在试一下。

3.方向导数存在的充分条件与计算

定理：如果函数z=f（x，y）在点P0（x0，y0）处可微分，那么函数在该点沿任一方向l 的方向导数都存在且有，其中cosα，cosβ 是方向l 的方向余弦。

证明：此处略，见教材[3-4]。

注：（1）本定理不但给出了方向导数存在的充分条件，而且给出了方向导数的计算方法。（2）方向导数的概念和计算公式可推广到三元函数上[3-4]。

（三）梯度

1.梯度的定义

先回顾引例1 与引例2 中的问题（2）：引例1 中的问题（2）——沿哪个方向，气压变化度最大？引例2 中的问题（2）——沿哪个方向，温度变化度最大？

再分析这两个问题的解决：由第一节知，事实上这两个问题都可以归结为沿什么方向导数最大？可转化为如下数学问题。

数学问题：u（x，y）为一个可微函数，P（x，y）是平面上一点为过P（x，y）的射线，则满足什么条件时，u（x，y）沿方向的方向导数取最大值？

虽然学生知道沿梯度方向，函数变化率，也即方向导数取最大值，但对梯度方向仍然没有直观认识，这就是会算却不会用，知识应用能力还没有得到很好的培养。为此，我们打算对引例进行数学实验验证，需要先介绍梯度的几何意义。

2.梯度的几何意义

梯度的几何意义：曲面u（x，y，z）=C 的梯度就是它的一个法向量，事实上

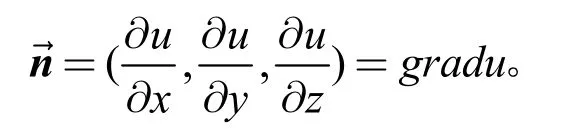
明白了梯度的几何意义后，就可以对引例进行数学实验验证了。

3.引例1 与引例2 的数学实验验证

引例1 的实验验证：飞机飞行高度不变，设飞行区的气压函数为P（x，y）=x2+2y2，飞机位于P0（1，2）点。问飞行员应该按照什么路线飞行才合理?

解：应该沿每一点处的梯度方向飞行。而梯度为gradp（x，y）=（2x，4y）。设飞机飞行路线为y=y（x），方向为其切向量s→=（1，y′）。则

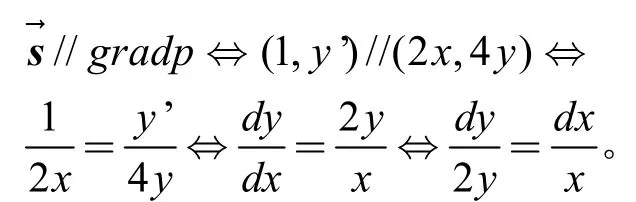
积分得y=Cx2，又过P0（1，2），所以y（1）=2，求得C=2。故飞行函数应该为y=2x2。

用matlab 画出等压线C=x2+2y2与飞机飞行路线y=2x2，如图1 所示，发现：直观上，飞行路线确实垂直于等压线，即为其法线。

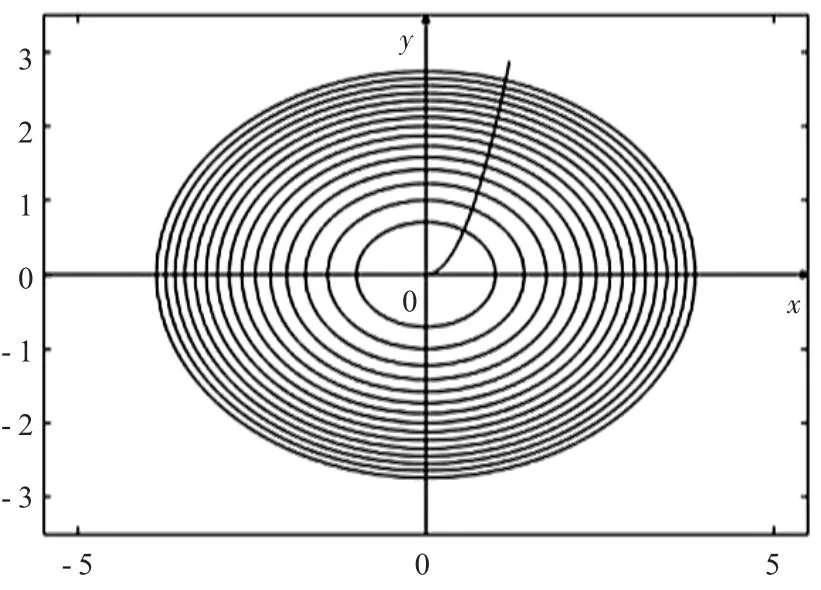
图1 引例1 的数学实验验证

引例2 的实验验证：设铁板温度函数为T（x，y）=100-x2-4y2，在P0（1，-2）处有一只蚂蚁。问蚂蚁沿什么路线逃跑，才能尽快逃到凉爽区？

注：推导过程类似于引例1 的实验验证，此处可采用分组讨论法，提高学生的学习参与性、培养团结协作精神。可求得蚂蚁逃跑函数应该为y=-2x4，用matlab 画出等温线与蚂蚁逃跑路线，如图2 所示，发现，直观上，蚂蚁逃跑路线确实垂直于等温线，即为其法线。

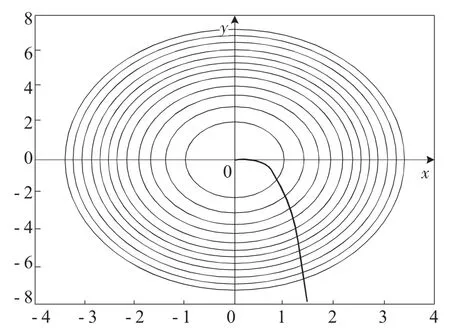
图2 引例2 的数学实验验证

概括起来，我们的方向导数与梯度的教学采用案例教学法，强化了学生的知识应用能力和创造性思维能力的培养，整个课堂教学流程图如图3 所示。

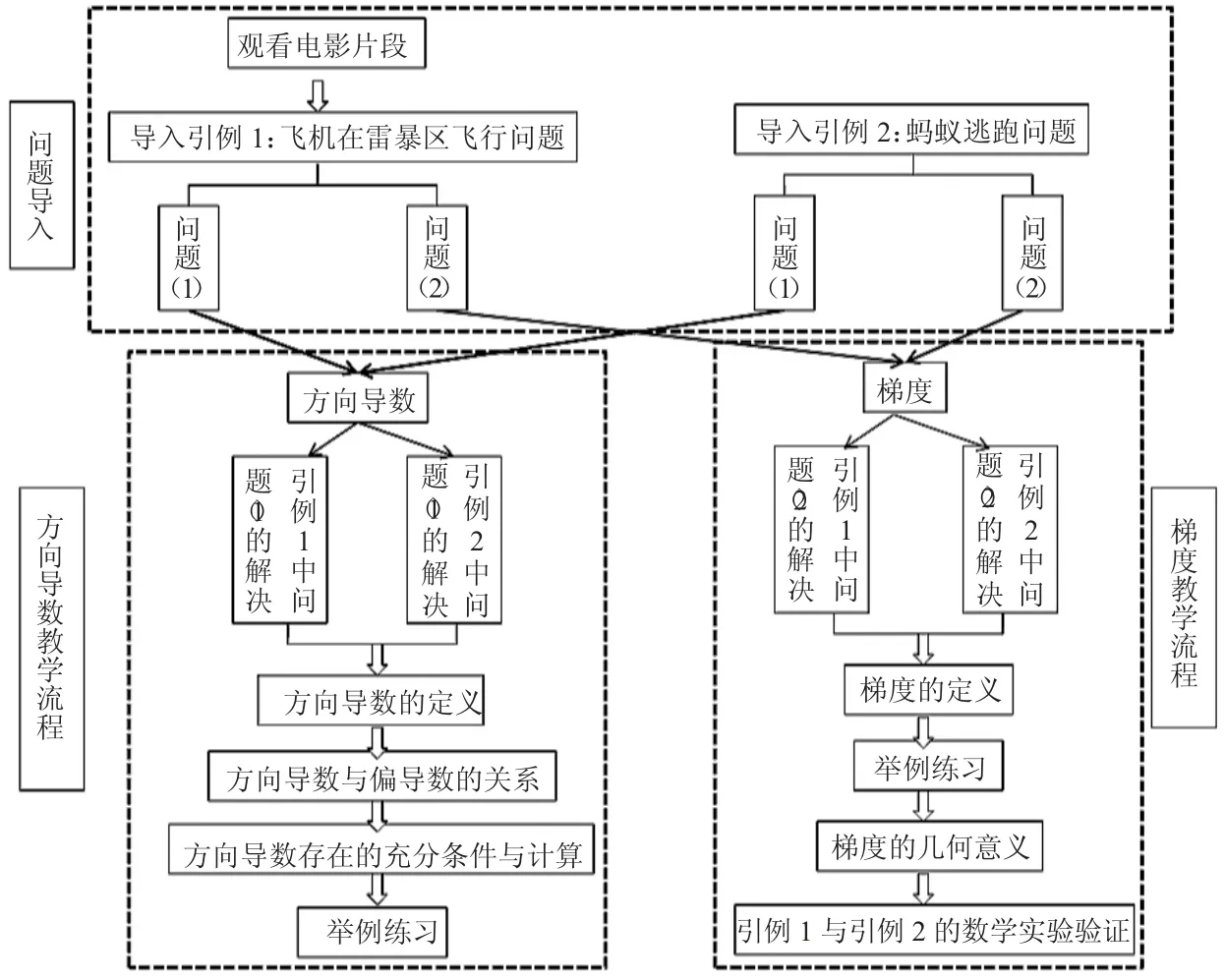
图3 教学流程图

四、结束语

案例教学法是实现以能力为导向的工科高等数学教学的有效途径。案例的应用性可以加深学生对数学知识应用背景的了解，提高对数学的学习兴趣，增强知识掌握效果，更好地实现教学目标中的知识目标；案例的分析、解决与实验验证过程可以培养学生的知识应用能力和创造性思维能力，有效促进教学目标中能力目标的达成，适应了工程教育专业认证与新工科建设等对数学教学的要求。评教结果与学习效果表明，基于案例的能力导向的高等数学教学受到了学生的欢迎，值得推广。