荆江河段沙市(二郎矶)站水位流量关系单值化方案优化分析
贺延虎
(长江水利委员会水文局 荆江水文水资源勘测局,湖北 荆州 434000)
0 引 言
目前,长江干流宜昌站[1]、监利(二)站[2]、螺山站[3]以及汉口站[4]等均采用综合落差指数法开展水位-流量关系单值化分析,效果较好。沙市(二郎矶)站是长江中游干流重要控制水文站,水位流量关系主要受洪水涨落和河段冲淤影响,特殊年份局部时段受下游洪水顶托影响,水位流量关系较为复杂。2009年底,沙市(二郎矶)站采用落差指数法开展水位-流量关系单值化方案[5](以下简称“方案”)分析,并通过评审,于2010年正式使用,该方案使用至今(2020年)在流量报汛、测次布置、推流整编等方面得到较好的检验。
随着三峡水库蓄水清水下泄,荆江河段河床下切明显。沙市(二郎矶)站基本水尺断面附近三八滩逐渐萎缩,大桥上游河段多年来持续进行航道疏浚、引江济汉分流等,导致河道水流情势发生较大变化,目前沙市(二郎矶)站采用的单值化校正流量点逐年右偏,全年需采用多条单值化线以及过渡曲线才能满足流量推算的要求,部分时段还需恢复连时序法布置测点、推流定线,造成测次布置时机难以掌握,工作量增加。因此,对沙市(二郎矶)站单值化方案进行优化分析是非常有必要的。
本文采用沙市(二郎矶)站2015~2020年水位、实测流量资料以及落差站水位资料,在原方案的基础上,对其中的参数进行试算优选。试算过程中,未遵循“落差系数和等于1”,而是采用不同的权重配比,选取最优的系数组合,确定了新的校正流量计算公式。本文采用新公式计算2015~2020年实测资料的校正流量,点绘水位校正流量关系线,进行3种检验和推流整编,并与原方案成果进行对比,以验证新公式的合理性。
1 研究区域与数据来源
沙市(二郎矶)站位于湖北省荆州市沙市区二郎矶,设立于1933年1月,是沙市河段的水沙代表站,同时又是长江中游干流的重要控制站和报汛站,对荆江地区防洪安全和防洪调度起到至关重要的作用。测验河段位于上荆江沙市河段。基本水尺位于沙市二郎矶,上游1 300 m处建有荆州长江公路大桥,左岸上游600 m处,17 km处,15 km处分别为观音矶、沮漳河入汇口和引江济汉工程取水口。右岸上游约14 km有太平口分流,约13 km处有荆江分洪工程进水闸。测流断面设在沙市柳林洲,在基本水尺断面下3 920 m处,位于长约4 km的顺直河段中部,测流断面下游约3.6 km有金城洲。
沙市(二郎矶)站水位流量关系主要受上游来水、断面冲淤和下游回水顶托影响,采用连时序法推流时,中高水期线型呈现典型的绳套状,绳套宽窄幅度与洪水涨落率关系明显,低枯水以单一线型为主。汛期河床冲淤变化较大,中高水主槽宽约1 170 m,深槽在起点距300~800 m间摆动,断面形状年内、年际均有一定变化。自2010年开始,沙市(二郎矶)站水位流量关系采用落差指数法进行单值化处理,处理方案适合该站应用。随着河段不断冲刷,沙市(二郎矶)站上下游落差关系发生明显变化,现有方案布置测次及定线推流时难度增加,2015年之后尤为明显。
本文分析资料选用沙市(二郎矶)站2015~2020年水位、实测流量和整编成果,资料样本中,2020年为丰水年份,2015年为枯水年份,其他年份为平水年份,资料代表性好;辅助水尺断面选用上游约16.7 km处陈家湾水位站,下游约49.3 km处郝穴(二)水位站,分别反映上游太平口分流及洪水涨落和下游回水顶托影响因素。
2 研究方法
2.1 原方案
沙市(二郎矶)站优化前的单值化方案为采用综合落差指数法对实测流量进行校正,其校正流量计算公式如下:
(1)
其中:
ΔZm=km1×ΔZm1+km2×ΔZm2
(2)
式中:q为校正流量,m3/s;Qm为实测流量,m3/s;k1为流量改正系数,取值1.0;k2为综合落差改正系数,取值1.0;ΔZm为综合落差,m;α为落差指数,取值0.55;ΔZm1为陈家湾水位落差,m;ΔZm2为郝穴水位落差,m;km1为陈家湾落差系数,取值0.215;km2为郝穴落差系数,取值0.787。
2.2 参数优化
沙市(二郎矶)站上游陈家湾站至沙市(二郎矶)站水位落差在0.30~0.90 m之间,受洪水涨落和河段冲於变化影响,随着水位上涨而减小;而沙市(二郎矶)站至下游郝穴站水位落差在1.40~2.80 m之间,受洪水涨落、河段冲於和下游顶托的共同作用,低水时随着水位上涨而减小,中高水时规律不明显。
本文在原方案的基础上,选用沙市(二郎矶)站2015~2020年6 a的数据,综合点绘水位校正流量关系图,通过调整km1,km2,α的数据,寻找规律。在调整km1,km2时,打破以往“系数和等于1”的固定思维,使用不同的系数配比,发现通过调大上游陈家湾至沙市落差系数km1,km2保持不变,可以明显修正系统偏离的水位校正流量点及突出点;反之则效果不明显,且km1,km2在0.80和0.70左右,对水位校正流量点的修正效果更好。调整α值时发现,α值在0.38~0.45之间时,水位校正流量关系点呈单一线型效果最好。
初定k1=1.0,k2=1.0,km1=0.80,km2=0.70,α=0.38,对选用的2015~2020年数据分别计算校正流量,并点绘水位校正流量关系图,计算定线标准差。通过对km1,km2,α进行微调、试算、对比,最终确定km1=0.80,km2=0.70,而α=0.42时适用性更好。代入校正流量计算基本公式,确定新的单值化方案:
(3)
其中:
ΔZm=0.80×ΔZm1+0.70×ΔZm2
(4)
3 结果分析
3.1 误差统计
采用优化后方案重新计算沙市(二郎矶)站2015~2020年校正流量并定线,各年水位校正流量关系点明显集中且成带状分布,优化后的方案计算沙市(二郎矶)站水位校正流量关系点较优化前更为集中,以2019年为例,如图1所示。
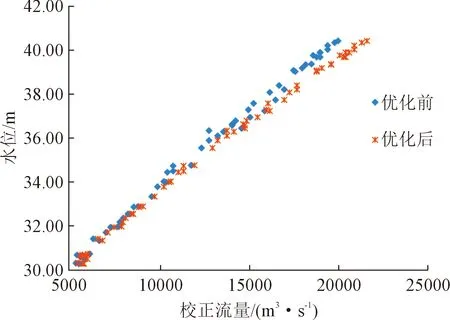
图1 2019年参数优化前后水位校正流量关系点Fig.1 Relation points of water level and correction flow before and after parameters optimization in 2019
经3种检验,各年定线精度均能满足现行规范要求。检验结果与优化前方案进行对比,相关指标统计见表1。
从表1可以看出,优化方案前后沙市(二郎矶)站水位流量关系单值化方案成果精度均达到或优于SL 247-2012《水文资料整编规范》中水位流量关系定线精度指标(一类精度水文站采用水力因素法的定线精度指标为系统误差不大于±2%,随机不确定度不大于10%)。优化前方案需要多条线,或是个别时段需要连时序法定线,才能满足推流要求;优化后方案定线数量少于优化前,定线推流方法更为简单,水位校正流量关系曲线更为简洁。
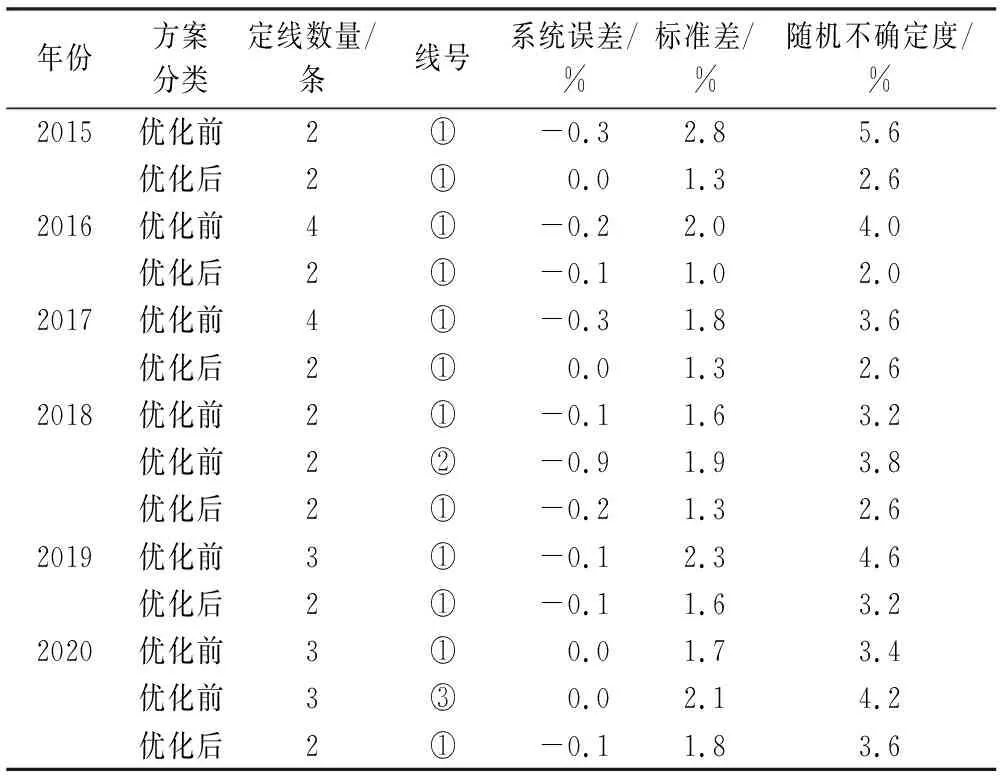
表1 定线检验误差对比Tab.1 Comparison of relationship curve accuracy
3.2 月、年最大最小流量
对比沙市(二郎矶)站优化前后方案推流成果,计算月、年的最大、最小流量相对误差。
相对误差=(优化后流量-优化前流量)/优化前流量×100%
(7)
统计结果表明,月最大流量相对误差在-4.1%~4.5%,在各流量级范围基本呈均匀分布,且最大相对误差出现在特殊水情(原方案中恢复了连时序定线或是采用过渡曲线推流);月最小流量相对误差在-6.2%~9.1%,大于±3%的主要出现在小流量级,即低、枯水期。年最大流量相对误差在-3.0%~0.3%,年最小流量相对误差在-2.9%~4.0%,误差较小,说明优化后的单值化方案推流成果可靠,统计结果见表2~3。
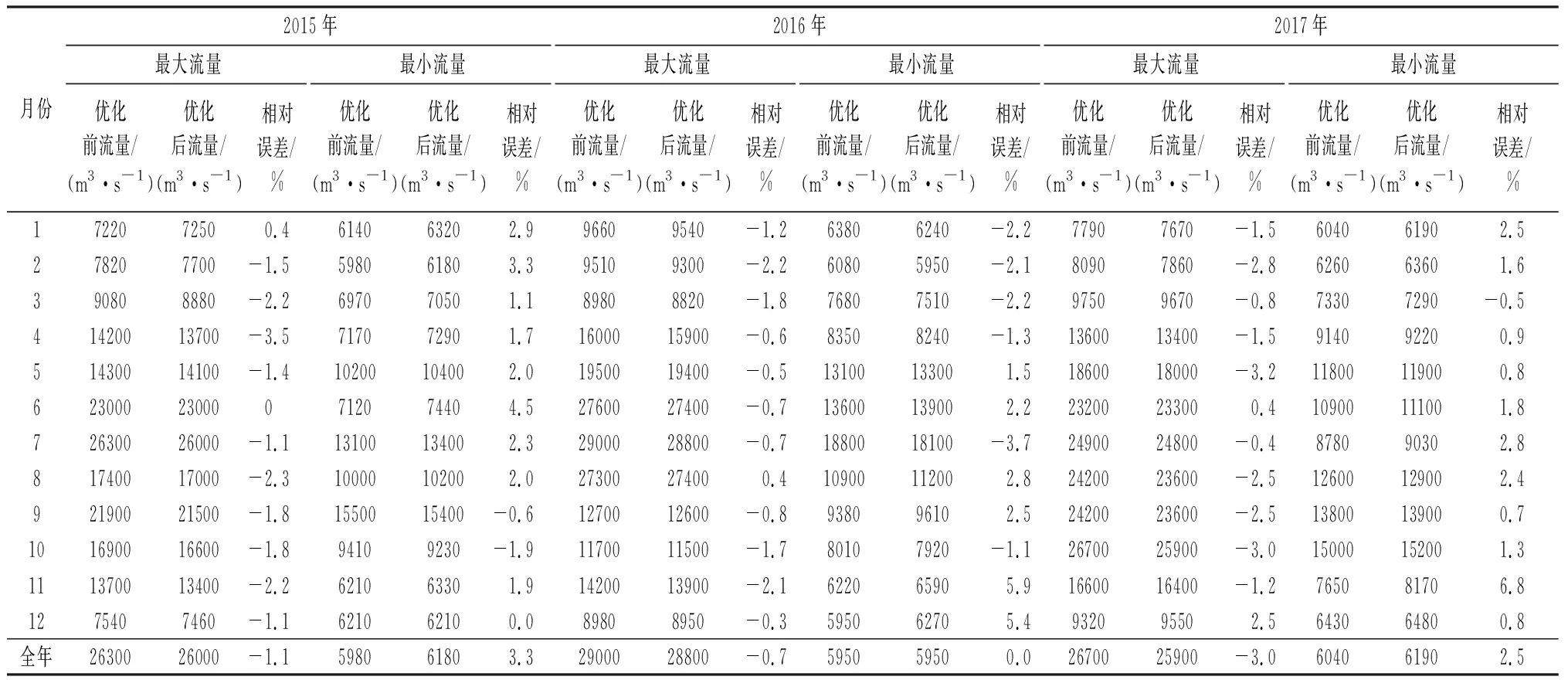
表2 参数优化前后月、年最大最小流量误差(2015~2017年)Tab.2 Errors of maximum and minimum monthly and annual discharge before and after parameters optimization from 2015 to 2017
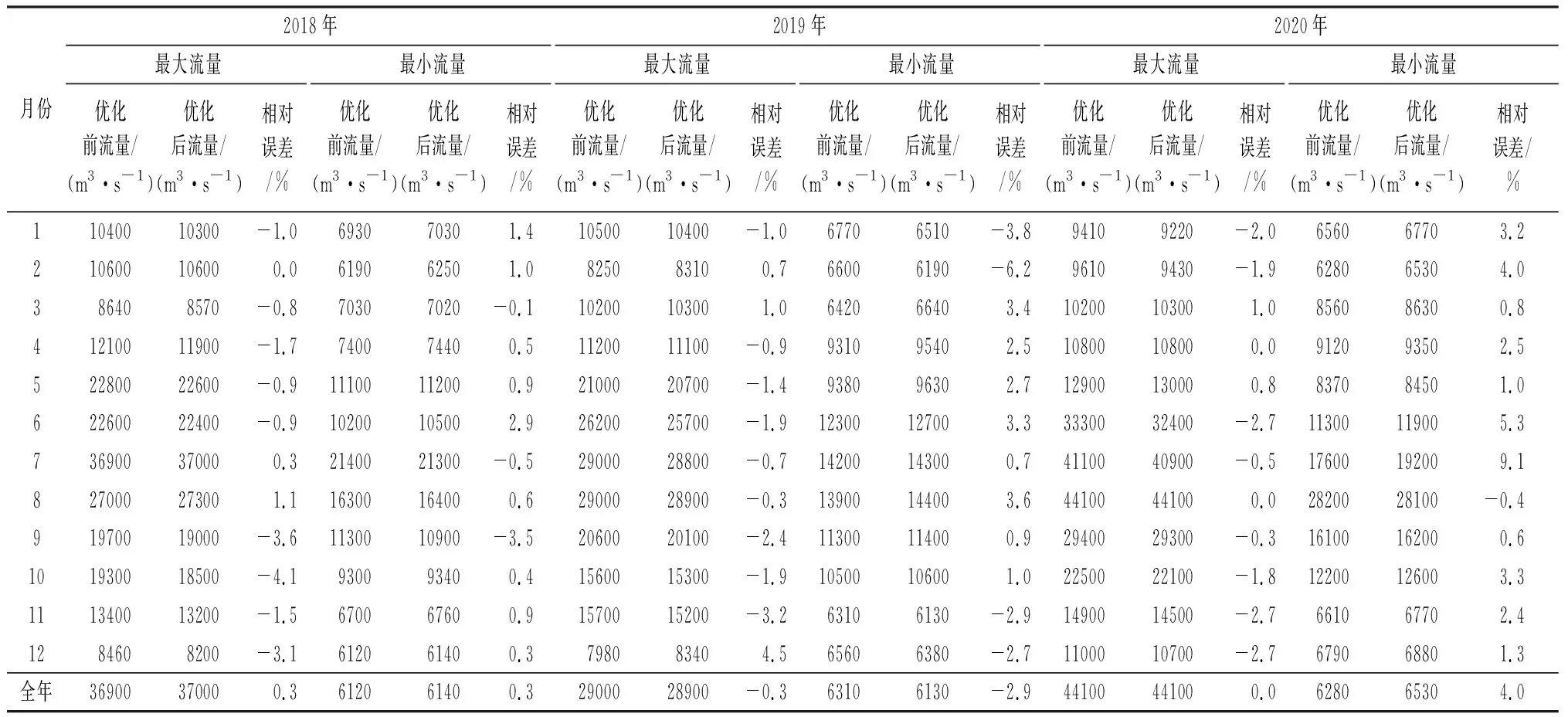
表3 参数优化前后月、年最大最小流量误差(2018~2020年)Tab.3 Errors of maximum and minimum monthly and annual discharge before and after parameters optimization from from 2018 to 2022
3.3 年内最大各日洪量
参照逐日平均流量表,对优化前后沙市(二郎矶)站方案推流成果中最大洪量统计分析,选取最大1 d,3 d,7 d,15 d,30 d,60 d最大洪量进行统计,计算相对误差。
相对误差=(优化后洪量-优化前洪量)/优化前洪量×100%
(8)
表4统计了最大各日洪量误差,2020年为丰水年,各日最大洪量相对误差在-1.1%~0.6%之间。2015年为枯水年,各日最大洪量相对误差在-1.1%~1.3%之间。2016~2019年平水年份,各日最大洪量相对误差在-2.7%~1.2%之间,且相对误差超过±2.0%时均出现在1 d和3 d基数较小的洪量级。
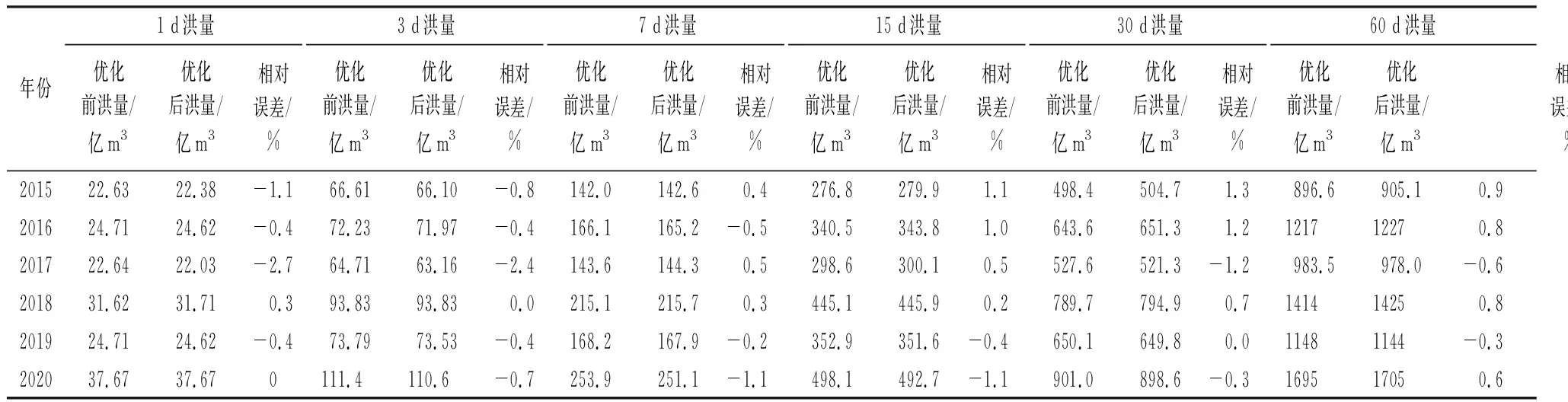
表4 最大各日洪量误差Tab.4 Errors of maximum flood volume
综合分析,优化后方案相对优化前方案推求的各日最大洪量误差较小,说明优化后的方案推流成果可靠。
3.4 年最大洪水过程线
选取2018年7月2日8:00至7月23日8:00年最大洪水,点绘方案优化前后沙市(二郎矶)站推流还原的洪水过程线图进行对照。如图2所示,过程线对应较好,大部分时段洪水过程线基本吻合,无系统偏离或是局部突出点,表明优化前后方案推求的洪水过程保持较好的相应性和完整性。
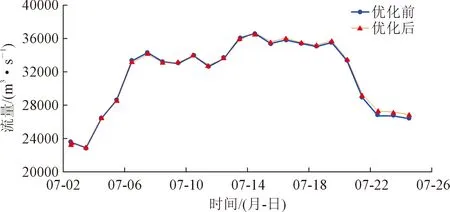
图2 2018年最大洪水过程线Fig.2 Maximum flood process lines in 2018
4 结 论
本文通过优化了沙市(二郎矶)站水位流量单值化方案,发现优化后的方案稳定性和通用性较好,可满足各年使用。优化后方案水位校正流量关系点更为集中,定线更简洁。说明沙市(二郎矶)站流量测验和资料整编可以按照优化后的沙市(二郎矶)站水位流量关系单值化方案来完成。使用优化后方案开展流量测验和整编时,遇到特殊水情或是汛前、汛后断面发生较大的冲淤变化的情况时,水位校正流量点距出现明显系统偏离,需要对系统偏离时段加密测次,单独绘制水位校正流量关系曲线或是采用分线处理,从而确保流量成果的精度。目前,沙市(二郎矶)站测验断面冲淤变化还未稳定,此次分析资料高水部分稍有欠缺,优化后方案依然存在局限性,后期还需进一步分析。

