一种利用双路相移布拉格光栅的快速微波频率测量方案*

李城鑫,毛久兵

(1.成都大学 电子信息与电气工程学院，成都 610106；2.中国电子科技集团公司第三十研究所，成都 611730)

0 引 言

在当今通信、导航、交通与自动控制、电子战及雷达等相关领域中，如何快速实现微波信号检测和分析至关重要。其中，微波频率作为测量的关键参数，已被广泛研究[1]。早期的电子式微波频率测量系统受“电子瓶颈”的限制，使得频率测量范围受限，且结构复杂、易受电磁干扰[2]。对此，微波光子技术因其低损耗、高带宽、抗电磁干扰及调谐灵活等优势可用来开展频率测量工作[3-12]。文献[3]提出基于特殊布拉格光栅的微波频率测量结构，该结构利用布拉格光栅的透射和反射特性实现1～10 GHz测频范围，但测频范围无法调谐。文献[4-5]提出基于互补光滤波器对的微波频率测量结构实现宽带测频，且测频范围具有可调谐性，然而测频范围受限于光滤波器的自由频谱范围(近似为自由频谱范围的一半)。文献[6-9]提出基于色散导致功率衰减效应的频率测量方案，可完成宽带测频，然而双调制器或双激光源的引入增加了系统的复杂度。文献[10-13]提出基于受激布里渊散射(Stimulated Brillouin Scattering,SBS)效应的宽带频率测量方案，可实现精度较高的频率测量，然而基于SBS的测量方案需配备高功率的泵浦光才能产生非线性效应，且易受环境影响。

针对文献[3-13]的不足，本文设计了一种结构简单、测频范围可大范围动态调整的微波频率测量系统，主要由一个相位调制器(Phase Modulator,PM)、两个相移布拉格光栅(Phase-shift Fiber Brag Gratings,PS-FBGs)和两个光环形器组成。其核心在于通过在上下支路引入具有不同陷波频率的PS-FBG，使得两支路输出呈现不同的功率峰值，进而利用上下支路功率比和待测微波信号频率之间映射关系建立幅度比较函数，实现微波频率测量。理论分析和仿真验证了该设计方案的有效性。

1 系统模型

设计的微波频率测量系统模型如图1所示，该系统由一个可调激光源(Tunable Laser Source,TLS)、一段保偏光纤(Polarization Maintaining Fiber,PMF)、一个PM 、一个光耦合器(Optical Coupler，OC)、两个光电探测器(Photodetectors,PDs)、两个具有不同陷波频率的PS-FBGs、两个光环形器(Optical Circulators)及后续处理设备组成。从TLS输出的光载波经由PMF后耦合进PM，用来调制待测信号。假定PM射频端输入的待测信号为Vin(t)=Vmcos(ωmt)，Vm和ωm分别为待测信号的振幅和角频率，可得PM输出光强如下所示[14]：

Eout(t)=Eoexp(jωct+jβcosωmt)。

(1)

式中：β=πVm/Vπ表示相位调制指数，Vπ为PM的半波电压；Eo和ωc分别为TLS的振幅和角频率。

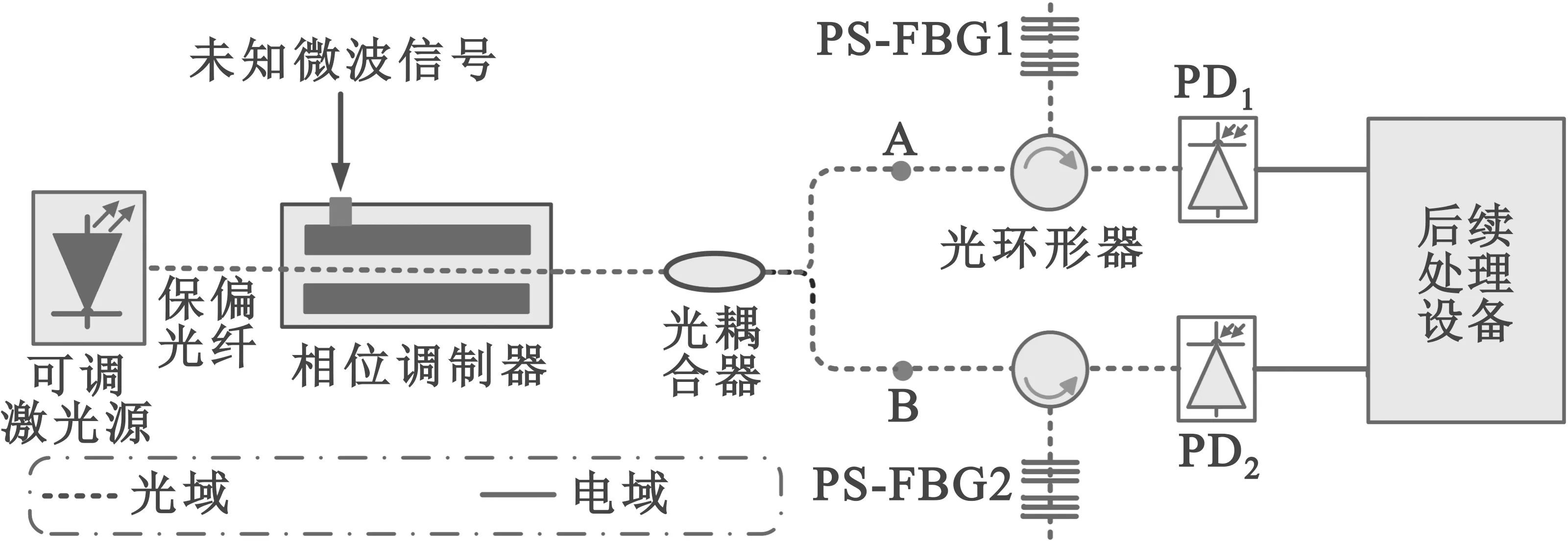
图1 设计的微波频率测量系统模型

对式(1)进行Jacobi-Anger展开，在小信号条件下可得

Eout(t)≈EoJ0(β)exp(jωct)+

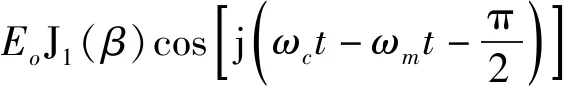
(2)

式中：Jn(·)为n阶第一类Bessel函数；当β<<1时，J0(β)≈1，J1(β)≈β/2。从PM输出的相位调制信号经过OC后，沿A支路和B支路分成两路信号。

A支路：该路信号经由光环形器后传输至PS-FBG1(PS-FBG1是由两个FBG级联而成，且两者之间的相移为π)。此处，PS-FBG1作为一个反射滤波器，用以抑制式(2)中的-1阶边带。通过PS-FBG1反射后，对应的输出光信号如式(3)所示：

“公司早期以把产品按照客户的需求做出来为目标，注重成品是否满足客户的设计与需求”，吴重蔚坦言，而随着时间的推移，栢科富翔尝试为客户提出建议，刚开始偏重于实物的建议，后来介入更高层次的设计环节。“公司专门成立了设计部，帮助客户做出更加合理的设计。有的客户甚至把整个项目交给我们来做，客户给出预算，公司则按照预算金额完成设计和制作。” 吴重蔚也表示，有时候客户描述得比较抽象，而使其具体化、图像化确是件不容易的事，但换个角度来看，设计师的理想与现实的差距就是企业生存的空间。

EPS-FBG1(t)≈EoJ0(β)exp(jωct)+

EoJ0(β)exp(jωct)+

Eoρ1(ωc-ωm)·

(3)

式中：r1(ω)表示PS-FBG1的反射系数；ρ1(ω)和ψ1(ω)分别表示r1(ω)的幅度和相位。它们的数学表达式如下[15]：

(4)

ρ1(ω)=|r1(ω)| ，

(5)

ψ1(ω)=phase[r1(ω)] 。

(6)

式中：iF11、iF22、iF21、iF12为iF中的元素，iF表示第i个 FBG的传输矩阵，iFmn表示矩阵iF的第m行第n列。iF中的元素可表示如下：

(7)

(8)

式中：*表示复共轭；zi表示PS-FBG1中第i个FBG的长度；γ2=κ2-σ2,σ=n·(ω-ωD)/c表示直流耦合系数，n表示有效折射率，ωD表示PS-FBG1反射谱中陷波角频率，c代表光速；κ=ω·Δn/(2c)表示交流耦合系数,Δn表示折射率变化。

从PS-FBG1反射的光信号利用PD1进行光电探测，可得探测后的微波信号光电流表达式如下：

(9)

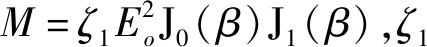
(10)

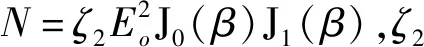
利用A、B支路光电探测器输出微波信号的功率比值构成幅度比较函数(Amplitude Comparison Function,ACF)，可表示如下：

(11)

从式(11)可知，该式反映了微波频率-功率映射关系。同时还可得出，ACF不是单调函数，与待测信号频率不是一一对应关系。对此，可选取0～fmax这一段ACF曲线呈单调性的频率范围，由该段频率范围的 ACF 值推测出唯一的待测信号频率，其中fmax表示ACF函数的第一个极值点；再参照式(4)～(10)可知，ACF由光载波频率和A、B两支路PS-FBGs的陷波频率共同决定。当这三个参数确定后，ACF与待测信号频率的映射关系即确定，进而在系统后处理阶段仅通过读取功率即可获取待测信号的频率[1]。

2 仿真结果及分析

为验证图1所示系统模型的性能，本节进行了相应的仿真。结构中，两个PS-FBGs具有以下相同的参数：z1=z2=3 mm,Δn=5×10-4,n=1.46。

2.1 测频分析

根据式(9)～(11)，设定激光源的光载波频率为193.1 THz，PS-FBG1的陷波频率为193.08 THz，PS-FBG2的陷波频率为193.078 THz时，A、B支路输出微波信号功率衰减函数如图2(a)所示，对应的ACF如图2(b)所示。由图可知，在0～20 GHz范围ACF曲线是单调递增的，ACF值与待测信号频率是一一对应关系，进而在这一段频率范围可由 ACF 值推测出唯一的待测信号频率。虽然ACF曲线在0～14 GHz区段较为平坦，具体细节如图2(b)所示，然而其灵敏度不小于0.2 dB/GHz,因此，理论上可在0～20 GHz的范围实现测频[13]。

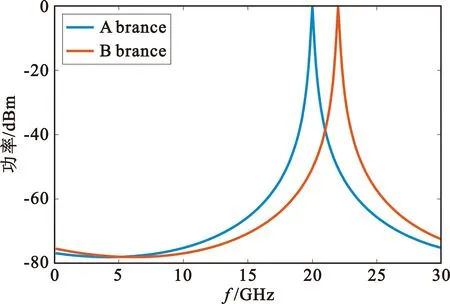
(a)A、B支路输出微波信号功率衰减函数对比曲线

2.2 PS-FBG1陷波频率对测频的影响

设定光载波频率和PS-FBG2陷波频率分别为193.1 THz和193.078 THz时，随着PS-FBG1陷波频率由193.080 THz不断向193.090 THz变化，对应的ACF曲线如图3所示。从图中可以看出，随着PS-FBG1陷波频率的不断增加，与光载波频率之间的间距也随之减小，使得ACF曲线的第一个单调区间逐渐变窄，分别为0～20 GHz、0～18 GHz、0～16 GHz、0～14GHz、0～12 GHz、0～10 GHz。与此同时，ACF 曲线的陡峭程度也随着PS-FBG1陷波频率的不断增加而增大，这意味着待测信号微小的频率变化所引起ACF值变化的程度也就越大，结果更直观、更容易被检测，频率的测量精度也随之提高。故随着PS-FBG1陷波频率的不断增加，频率测量范围随之减小，频率的测量精度则不断提高。

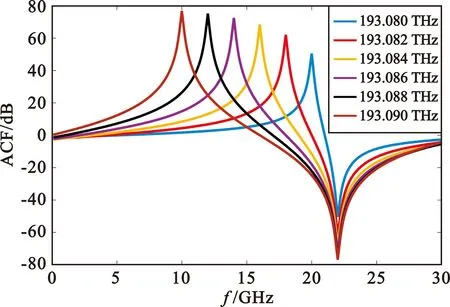
图3 不同PS-FBG1陷波频率下的ACF曲线

2.3 光载波频率对测频的影响

2.2节中PS-FBG1陷波频率的改变，需重新引入PS-FBG对系统进行重配置，测频范围的改变无法连续完成。为此，此节分析光载波连续调节下对测频的影响。设定PS-FBG1和PS-FBG2陷波频率分别为193.080 THz和193.078 THz时，光载波频率从193.1 THz向193.090 THz变化，调节步长为2 GHz，对应的ACF曲线如图4所示。由图可得出，随着光载波频率的不断减小，与PS-FBG1陷波频率之间的间距也随之变窄，测频范围也随之减小，分别为0～20 GHz、0～18 GHz、0～16 GHz、0～14 GHz、0～12 GHz、0～10 GHz。同时，ACF曲线的陡峭程度也随着光载波频率的不断减小而增大，频率的测量精度也随之提高。

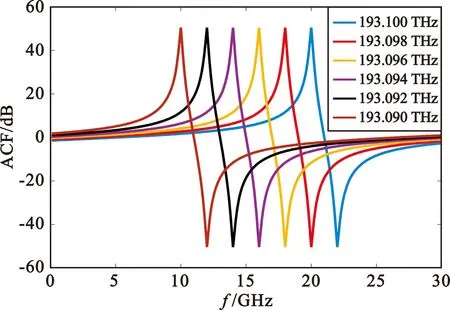
图4 不同光载波频率下的ACF曲

2.4 测频精度和实时性分析

根据以上分析可知，调节光载波频率会改变系统的测频范围和测量精度。为获得高的频率测量精度，采用两步测量法。第一步，先调节光载波频率，获得大的频率测量范围，大致测量出待测信号的频率。第二步，后续处理设备再根据输出信号的频率调节光载波频率，使待测信号的频率位于ACF曲线第一个单调区间内峰值附近陡峭程度较大的区段，意味着待测信号小的频率变化将导致 ACF值较大程度的改变，故测得的频率精度较高。同时，在两步测量过程中，第一步大范围低精度测量的光载波调节可在频率测量前完成，因此在整个测频过程中仅需调节一次光载波频率即可完成高精度测频工作，故可实现快速测频。

3 结束语

本文设计了一种基于双路PS-FBGs的快速频率测量系统，通过上下支路采用具有不同陷波频率的PS-FBGs，再与PM和激光源进行融合处理，构建幅度比较函数，用于检测待测信号的频率。相比较现有的测频系统，本文设计的系统具有结构简单的特点。分析结果表明，通过调节激光源的载波频率，可改变频率测量范围和测量精度；再采用两步测量法，将大范围频率粗测量和小范围频率细测量进行融合，实现高精度的微波频率测量。因此，该系统在宽带高精度测频领域特别是雷达、电子战等系统的前端频率测量中有较好的应用前景。

下一步工作将围绕着如何实现系统的小型化、集成化展开，以满足实际应用的需求。