基于残差神经网络的无人机射频信号识别*

杨小伟，王泽跃，杨鹤猛，杨 雪，张莉莉，陈艳芳

(1.国网天津市电力公司城西供电分公司，天津 300301；2.天津航天中为数据系统科技有限公司，天津 300301)

0 引 言

近年来，无人机的普及给公共安全、个人隐私、低空领域安全造成了极大的隐患，无人机误入机场、军事区域等事件也频有发生，因此对无人机进行侦察管控变得至关重要。

通过探测无人机与其控制器通信的射频信号并对其识别是一种有效的侦察无人机的方法[1-3]。由于在无人机中使用特定频率的射频信号，因此可以从智能手机和笔记本电脑等设备发射的所有其他无线电频率中识别无人机通信信号。射频分析能更准确地识别无人机，在某些情况下也可以识别出无人机的型号和品牌。

目前，许多学者都通过无人机与遥控间的通信信号进行无人机识别，主要分为使用射频指纹等传统信号分析方法进行识别和通过深度学习方法进行信号识别[4-6]。

采用射频指纹方法的工作通常是通过传统方法提取信号特征对信号进行识别。文献[1]通过跳频信号和图传信号识别无人机信号特征来进行无人机监测。文献[2]采用图像分类的方式对跳频信号进行识别，取得了不错的效果，但跳频信号容易遭到噪声干扰，导致识别效果差。文献[3]采用分形贝叶斯变点检测算法检测瞬态起始点并提取指纹特征进行识别，但该方法只能区分不同型号间的无人机，无法对同一型号的不同无人机个体进行区分。

采用传统方法进行无人机信号识别虽取得了不错的效果，但这些方法需要对信号进行大量的预处理操作，且需具备无线通信方面大量的专业知识，而采用深度学习方法将大大简化这个过程。文献[4]使用深度学习算法对公开无人机数据集进行信号识别，采用深度神经网络(Deep Neural Network,DNN)的方法实现了无人机型号和飞行模式的识别。文献[5]和文献[6]都是在文献[4]的基础上进行提升：文献[5]采用卷积神经网络对预处理后的信号进行特征提取并识别，但该方法设计的神经网络模型较为简单，效果相较于基准方法提升不明显；文献[6]采用机器学习的方法对无人机信号进行分类，但该方法所需要的预处理操作更繁杂，且该方法更适合于小样本学习，当数据较多时所需的时间成本和计算复杂度将大大增加。

本文提出了一种基于残差神经网络的无人机信号识别算法，旨在根据采集到的无人机射频信号对无人机是否存在、无人机型号和无人机运行模式进行识别。相比较于文献[4]和文献[5]，本文提出的方法根据无人机信号特征所设计的残差神经网络能有效防止过拟合，解决网络退化问题，识别准确率有明显提升。相比较于文献[6]，本文提出的方法所需的预处理操作更少，且模型的泛化性和适应性更好。同时，相比较于常用的残差网络结构，本文方法根据无人机一维信号的特征，采用一维的卷积核及池化核，根据数据量及信号特征设计网络深度，最终取得了更好的识别效果。

1 数据集及其预处理

深度学习是在大量的数据基础上进行模型训练和测试，本文使用了一个开源数据集DroneRF[7]进行模型训练。该数据集主要收集不同型号的无人机在不同运行模式下的射频通信信号，无人机的类型主要包括Parrot Bebop、Parrot AR和DJI Phantom。这些无人机主要用于民用研究，其大小、价格、性能和技术都不相同。此外，该数据集由454个射频信号记录组成，每段记录包含代表所采集信号振幅的100万个样本。除了无人机的射频信号外，该数据集还包含了没有无人机活动的信号记录。该数据集不仅可以识别无人机是否存在，也能利用无人机的射频信号特征对无人机的类型和运行模式进行识别。表1为该数据集的数据分布，无人机的主要类型为没有无人机、Bebop、AR和Phantom。此外，该数据集包含了在各种模式的无人机中捕获的射频信号，如开启和连接、悬停、飞行、飞行并录像。其中，包含无人机活动的数据占数据集总量约82%，没有无人机活动的记录占约18.06%。没有无人机活动的数据即背景活动数据，有利于降低噪声信息的干扰。

数据集中的原始数据是用射频接收设备进行采集，无法直接作为训练数据，因此在使用神经网络进行训练之前还需要对原始数据进行预处理操作。由于每台射频信号接收器的最大瞬时带宽为40 MHz，因此需要使用两个射频信号接收器同时操作来捕获带宽80 MHz的WiFi信号，第一台接收器捕获低频段40 MHz带宽的频带，第二台接收器捕获高频段40 MHz带宽的频带，两个接收器采集的数据长度一样，分别计算两段数据的离散傅里叶变换：

(1)

(2)

式中：xi(L)和xi(H)分别是第一台信号接收器接收到的低频段频带和第二台信号接收器接收到的高频段频带的第i段射频信号；yi(L)和yi(H)是分别来自两台信号接收器的第i段射频信号频谱；n和m分别为xi和yi的索引号；N是射频信号段总数。

将高频段射频数据进行缩放，并接入到低频段射频数据的尾端，从而将两个接收器的转换信号连接起来，以建立完整的射频信号：

(3)

(4)

式中：c是一个归一化因子，其值为低频段数据的最后Q个频点值和高频段数据的前Q个频点值之比；M是将高低两部分的频段连接后yi的总频点数，即第i段射频信号样本数据长度。使用归一化因子c将高低两部分的频段数据连接起来，从而确保了使用不同设备捕获的两段射频信号之间的频谱连续性。值得注意的是，Q必须相对较小才能成功缝合两段信号，且需足够大才能平衡随机波动造成的影响，本文中Q取值为10。M取值2 048，即通过连接信号数据得到了长度为2 048的射频信号样本。原始RF信号片段如图1所示，X(L)和X(H)振幅归一化为-1～1，分别用蓝色和红色表示。

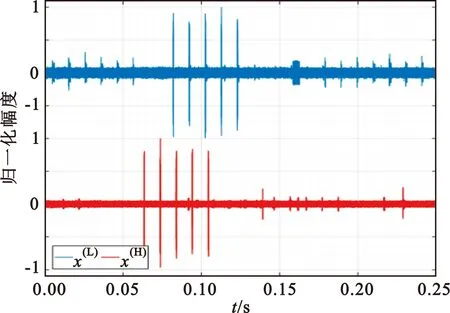
(a)背景信号

2 基于残差网络的无人机识别算法

2.1 基准网络介绍

深度神经网络是深度学习的一种基本网络，由输入层、输出层和隐藏层组成。基准网络[7]使用DNN对无人机信号进行分类，如图2所示，第0层为输入层，第1～L-1层为隐藏层，第L层为输出层。其中，H(l)表示第l层的神经元个数，C为分类器的类别数。使用3个深度神经网络分别预测无人机是否存在、无人机的类型、无人机的运行模式。

2.2 残差神经网络

残差网络的主要优点是将卷积层的前后连接起来，通过卷积层和池化层来提取信号特征，利用残差网络跳跃连接的特性，在网络层数较深的情况下在网络中多个尺度上提取特征，防止过拟合和梯度消失，解决网络退化的问题，从而提高识别精度。图3为残差单元的结构图，卷积层的输入x与残差函数F(x)的维度需保持一致以满足相加运算的条件，记输出函数为H(x)，根据残差特性可得到

H(x)=x+F(x)。

(5)

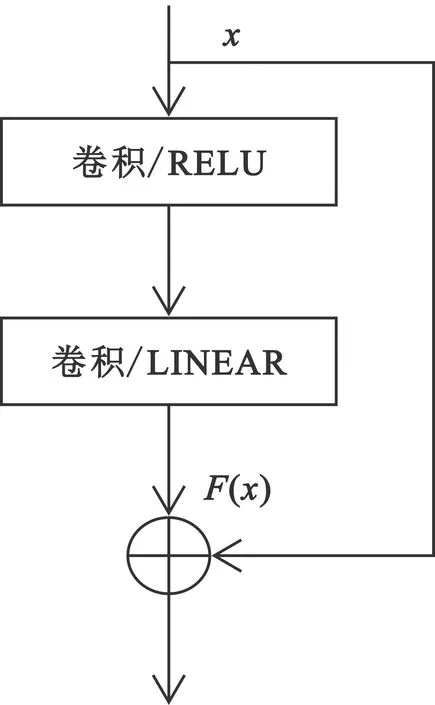
图3 残差单元

本文使用的残差网络基本结构如图4所示，整体网络结构及输出大小如表2所示。针对无人机信号是一维数据的特征，网络的输入尺寸为1×N，1表示特征通道数，N表示采样点个数，将数据经过矩阵变换操作后，输入数据转换为1×N×1。网络结构共包含3个残差块，每个残差块包含两个跳跃连接，跳跃连接之间包含两个卷积层、批标准化层和一个激活函数用于特征提取。与传统的残差结构相对比，将批标准化层和激活函数置于卷积层之前作为预激活，使网络更易于优化，并减少过拟合的现象。在残差块的最后加入最大池化层。其中，卷积层通道数为32，卷积步长为2，卷积核大小为3×1，池化核大小为2×1，激活函数使用渗漏整流线性单元(Leaky Relu)函数。整个网络结构使用3个残差块，同时通过使用两个全连接层和Softmax层以输出类别数量大小的特征向量，在网络中加入dropout层以防止网络在训练过程中出现过拟合的现象。

图4 残差块基本结构

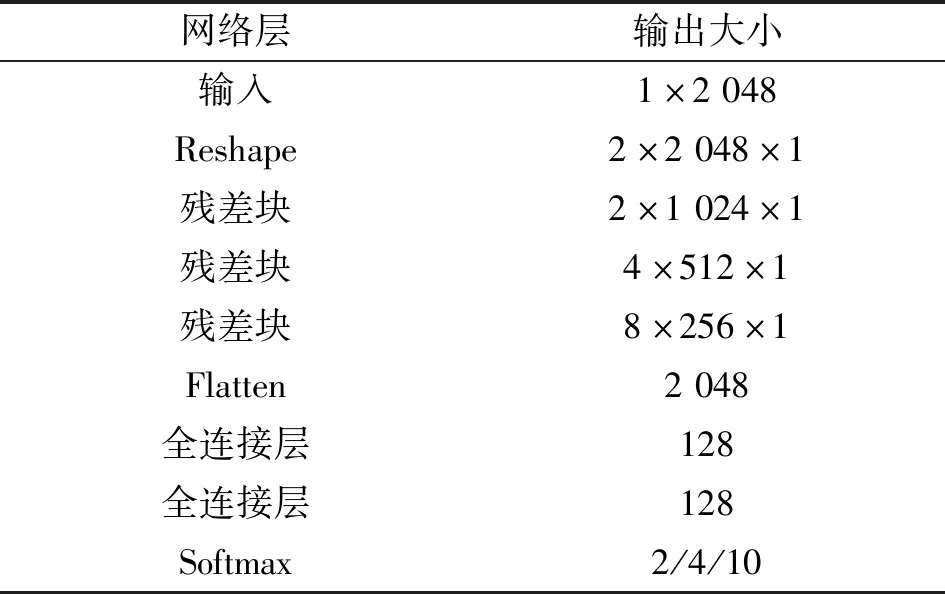
表2 网络框架及输出

根据DroneRF数据集的特性，无人机信号数据被预处理为1×2 048大小的输入数据。由于无人机信号为一维数据，采用太深的卷积神经网络容易造成过拟合、对噪声的适应能力差的问题。因此，本文设计的网络采用了残差结构，且使用3个残差块进行特征提取，从而避免了网络过深导致的网络退化问题。同时，由于输入数据的形式为1×N，因此将网络中原本为3×3大小的卷积核和2×2大小的池化核分别改为3×1和2×1大小。由于无人机识别包含不同的分类任务，因此，在最后的Softmax层可以根据分类任务的不同设置不同的分类输出，包括二分类以识别无人机存在、四分类以识别无人机型号以及十分类以识别无人机运行模式。

模型训练采用了交叉验证的方法。该方法是一种重复K次的迭代过程，从而在低偏差和方差的情况下得到模型的性能。该方法首先将数据集中的样本平均分为K份，每份数据中各类的样本数量相同。然后，在之后的每次迭代过程中将第K份数据作为测试集，其他的数据则作为训练集。将此迭代过程重复K次从而能将整个数据集都被模型测试，最后将K次的平均性能作为模型的性能评估[8]。

3 实验分析

3.1 实验步骤和实验方法

本文使用Matlab R2016a对数据集进行预处理操作，将从信号接收器采集得到的原始数据进行分段、频域转换、聚合、数据标注、归一化、维度转换等操作，最终生成1×2 048×1大小的数据以输入深度学习神经网络进行训练。其中，公式(4)中M设置为10，Q设置为2 048。

交叉验证实验中K的值设置为10，训练过程中，将学习率设置为0.001，批尺寸(batch_size)设置为10，实验采用Keras深度学习框架，训练环境为Ubuntu 16.04操作系统，NVIDIA GTX 2060 Super GPU计算平台。

3.2 评价指标

无人机信号识别模型的平均性能使用准确率(accuracy)、精确度(precision)、召回率(recall)、错误率(error)、错误发现率(False Discovery Rate,FDR)、假负率(False Negative Rate,FNR)、F1分数(F1 score)进行衡量，其计算公式分别如下：

(6)

(7)

(8)

error=1-accuracy,

(9)

FDR=1-precision,

(10)

FNR=1-recall,

(11)

(12)

式中：TP、TN、FP、FN分别为真正例、真负例、假正例、假负例。

3.3 实验结果分析

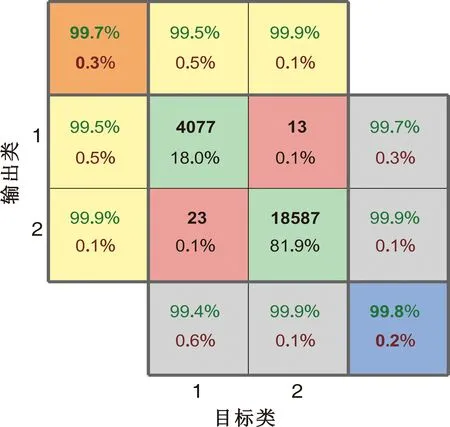
如图5所示，对角线上绿色块中表示正确分类的数据段，而非对角线上的红色块表示错误分类的数据段。其中的内容分别是数据段及其所占总数据段的百分比，最右边的灰色列绿色字体表示精度，红色字体表示FDR。此外，底部的灰色行绿色字体表示召回率，红色字体表示FNR；右下角的蓝色单元格绿色字体表示整体准确率，红色字体为错误率。左侧和顶部的黄色块中，绿色字体为F1分数，红色字体则为1-F1分数。左上角的橙色块绿色字体表示整体的F1分数，红色字体表示整体的1-F1分数。

(a)二分类结果

如图5(a)所示，在对无人机是否存在进行识别的情况下，整体准确率达到了99.8%，平均错误率为0.2%，平均F1分数为99.7%。如图5(b)所示，对无人机型号进行识别分为4类，其整体准确率达到了91.1%，平均错误率为8.9%，平均F1分数为92.9%。如图5(c)所示，对无人机的飞行模式进行识别分为10类，其整体准确率达到了70.3%，平均错误率为29.7%，平均F1分数为66.9%。

将本文方法与其他方法进行比较，结果如表3所示。本文提出的方法相对于基准方法DNN，识别无人机存在的准确率提升了0.2%，识别无人机型号准确率提升了6.6%，识别无人机运行模式的准确率提升了23.5%。

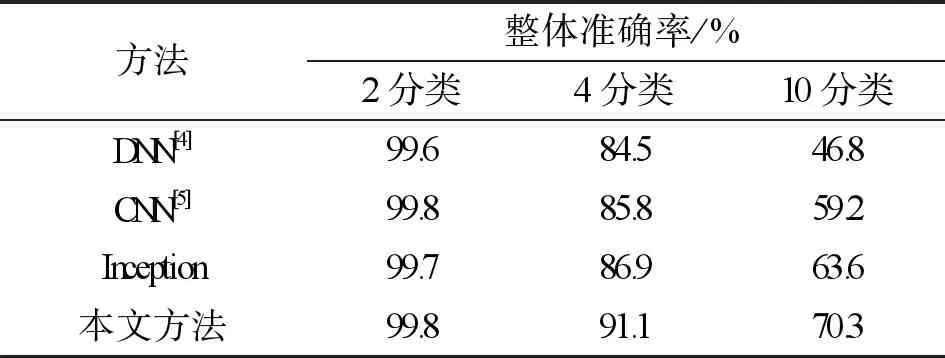
表3 本文方法与其他方法的准确率对比

将本文方法与其他方法进行时间性能的比较，表4所示为不同网络模型的参数量和检测一条1×2 048大小的样本所耗费的时间。基准方法DNN仅包含输入、输出及全连接层，网络层数仅有4层，本文方法相比较于基准方法，网络层数远比基准方法更深，但在检测所耗费的时间上仅比基准方法略高，且本文方法的时间性能明显优于其他方法。

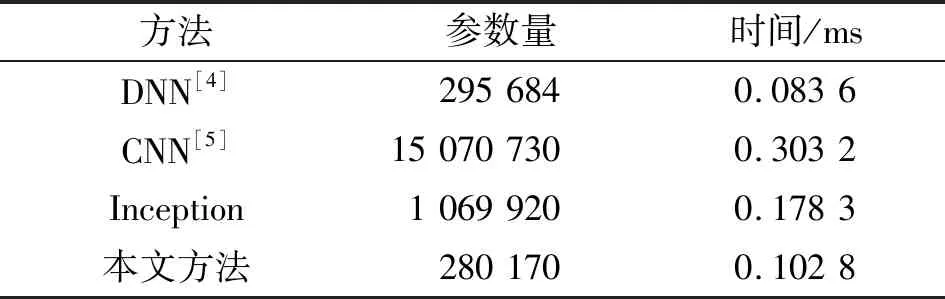
表4 本文方法与其他方法参数量及时间性能对比

4 结 论

本文提出了一种基于残差网络结构的无人机信号识别方法，通过学习无人机与控制器之间的通信信号特征来识别无人机是否存在、无人机的型号以及无人机的运行模式。本文方法首先对数据集中的原始数据进行分段、频域转换、聚合、数据标注、归一化、维度转换等简单的预处理操作，然后将处理后的数据送入改进的残差网络结构进行训练，最后使用训练好的模型进行实时识别。实验结果验证了通过无人机信号识别无人机的有效性，同时表明基于残差网络结构的无人机识别方法的识别准确度明显优于其他方法。