阵元失效下基于核范数和SCAD惩罚的MIMO雷达DOA估计*

陈金立，付善腾，朱熙铖，李家强

(南京信息工程大学 a.气象灾害预报预警与评估协同创新中心;b.电子与信息工程学院，南京210044)

0 引 言

多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达利用多个发射天线同时发射相互正交信号，多个接收天线接收目标回波信号并对其进行匹配滤波器处理，大大增加了虚拟阵元数，从而获得更大的阵列自由度和阵列孔径。与传统相控阵雷达相比，MIMO雷达在抑制干扰、提高空间分辨率和增强参数可辨识性等方面具有明显的优势[1]。

波达方向角(Direction of Arrival,DOA)估计是MIMO雷达信号处理中的重要研究内容，主要有子空间类[2-3]和基于稀疏表征类[4]等DOA估计方法。在实际应用中，随着阵列规模的不断扩大，在恶劣自然环境、人为干扰和阵元老化等因素的影响下，拥有较多收发天线的MIMO雷达不可避免地出现阵元失效问题，MIMO雷达经过匹配滤波后所形成的虚拟阵列中存在大量失效虚拟阵元，致使虚拟阵列协方差矩阵出现大批整行整列的数据缺失，从而破坏阵列数据结构完整性，这不仅会减少MIMO雷达最大可识别目标数，而且会严重降低DOA估计性能。

针对阵元失效条件下的DOA估计问题，文献[5]将单快拍下接收数据中元素重排，以满足随机分布条件，然后利用矩阵填充方法(Matrix Completion,MC)算法填补缺失数据，但该方法逐个快拍进行数据恢复的计算复杂度很高，且DOA估计精度较低。文献[6]针对冗余阵元失效情况，通过虚拟差分阵列中的冗余阵元数据来填补故障阵元的缺失数据；对于非冗余阵元失效情况，将差分阵列协方差矩阵扩展为存在数据缺失的高维Toeplitz矩阵，然后利用MC实现对缺失数据的恢复。文献[7]利用互质阵列协方差矩阵的低秩特性和Hermitian Toeplitz结构来重构完整协方差矩阵，但大多数情况下MIMO雷达虚拟阵列协方差矩阵具有块Toeplitz结构，因此在MIMO雷达中无法直接利用互质阵列的特性来恢复缺失数据。文献[8]提出一种基于块Hankel矩阵填充的MIMO雷达失效阵元缺失数据恢复方法，将接收数据协方差矩阵转换成具有四重Hankel结构的构造矩阵，使重构后的矩阵每行每列均存在非零元素，然后利用MC算法填补缺失数据，但该方法所构造的Hankel矩阵维度庞大，使得计算复杂度高，运算时间较长。现有基于MC理论的阵元失效DOA估计方法都是先对阵列输出数据矩阵中元素进行重排，在保证低秩性的同时使矩阵内缺失数据的每行每列都存在非零采样数据，利用 MC算法能顺利重构出完整矩阵，从而提高DOA估计性能。在实际应用中，由于目标的个数小于MIMO雷达的虚拟阵元数，因此其接收数据矩阵具有低秩特性，当出现整行整列的缺失元素时，仅利用低秩特性无法提供有效的正则化表达。文献[9]在逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)中利用采样矩阵的低秩和稀疏特性，分别在频率和方位角维度构建过完备傅里叶字典来恢复缺失数据，但该方法计算复杂度较高。

为了恢复阵元失效下MIMO雷达协方差矩阵中整行整列的缺失元素，以提高其DOA估计性能，本文对待恢复的协方差矩阵建立核范数和SCAD(Smoothly Clipped Absolute Deviation)惩罚联合约束模型，然后通过等正弦空间稀疏化方式划分粗网格空间构建字典。该方法对缺失数据恢复带来的误差可以忽略不计，能有效降低计算复杂度，并利用ALM-ADMM(Augmented Lagrange Multipliers-Alternating Direction Method of Multipliers)算法来求解双先验约束模型，从而恢复因阵元失效而导致的大量整行整列的缺失数据，最后通过RD-ESPRIT(Reduced Dimensional ESPRIT)算法估计目标的DOA。仿真实验表明，本文方法能快速重构完整协方差矩阵，有效提高DOA估计精度。

1 阵元失效MIMO雷达信号模型

假设MIMO雷达具有M个发射阵元和N个接收阵元，其中发射阵列和接收阵列共置且都是均匀线阵，远场存在P个非相干目标，其入射角度分别为θ1,θ2,…,θP，则接收阵列在第q脉冲周期的接收信号为

(1)

式中：Ar=[ar(v1),ar(v2),…,ar(vP)]∈N×P为接收阵列的流形矩阵,其中，ar(vp)=[1,ej2πdrvP/λ,…,ej2π(N-1)drvP/λ]T∈N×1，dr为接收阵元间距，vp=sin(θp)，λ为载波波长，(·)T表示矩阵转置，表示复数域；At=[at(v1),at(v2),…,at(vP)]∈M×P为发射阵列的流形矩阵，其中，at(vP)=[1,ej2πdtvP/λ,…,ej2π(M-1)dtvP/λ]T∈M×1，dt为发射阵元间距；B∈M×L为发射信号波形矩阵；Nq∈N×L表示第q个脉冲周期内均值为零的加性高斯白噪声，L为每个脉冲周期内的相位编码个数；diag(sq)表示由矢量sq构成的对角矩阵，其中，sq=[β1ej2πqfd1/fs,β2ej2πqfd2/fs,…,βpej2πqfdp/fs]T，βp表示第p个目标的反射系数，fdp表示第p个目标的多普勒频率，fs为脉冲重复频率。Q个脉冲周期的回波信号经过匹配滤波后，可获得MN×Q回波信号矩阵：

Y=(Ar⊙At)S+Z。

(2)

式中：Y=[y1,1,y1,2,…,yM,N]T∈MN×Q，其中ym,n=[ym,n(1),ym,n(2),…,ym,n(Q)]T为第(n-1)×M+m个虚拟阵元的输出信号；S=[s1,s2,…,sQ]∈K×Q是目标系数矩阵；Z=[z1,1,z1,2，…,zM,N]∈MN×Q为零均值高斯白噪声矩阵，其中zm,n=[zm,n(1),zm,n(2),…,zm,n(Q)]T为第(n-1)×M+m个虚拟阵元的噪声信号矢量；Ar⊙At表示虚拟阵列流型矩阵，⊙表示Khatri-Rao积。

(3)

(4)

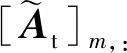
(5)

经过上述置零处理后，阵元失效下MIMO雷达虚拟阵列输出信号为

(6)

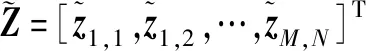
虚拟阵列协方差矩阵在Q个脉冲周期下的最大似然估计为

(7)

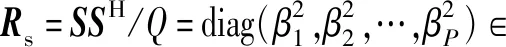
2 基于协方差矩阵核范数和SCAD惩罚的MIMO雷达DOA估计方法

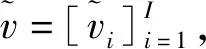
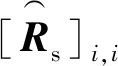
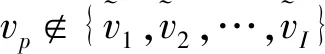
(8)

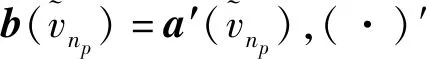
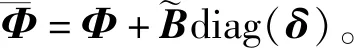
(9)

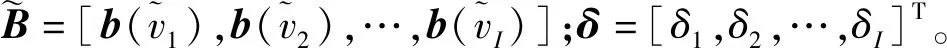
(10)

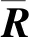
当矩阵中存在整行整列缺失数据时，矩阵填充中最小化秩无法提供有效的正则化表达，因此采用核范数和SCAD惩罚来联合正则化矩阵的行和列，这样不仅能利用行和列间元素的相关性。而且还能充分利用行内和列内元素的相关性。建立如下矩阵填充模型：

(11a)

(11b)

(11c)

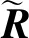
(12)

式中：ξ为调整参数；a为常量。

式(11)的优化问题可以用ADMM框架下的增广拉格朗日乘子法(Augmented Lagrange Method,ALM)来求解，可以表示为

(13)

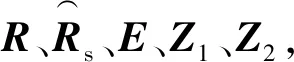
。(14)

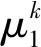
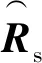
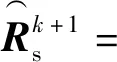
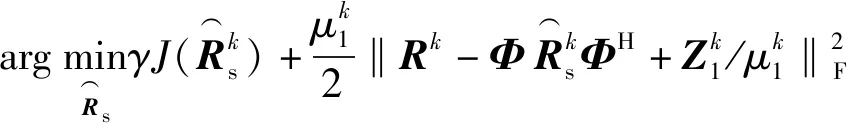
(15)

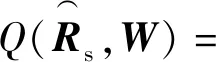
(16)

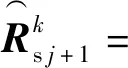
(17)

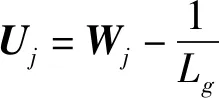
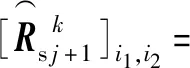
(18)

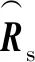
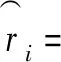
(19)

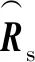
(20)

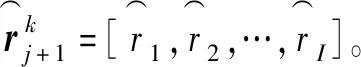
(21)

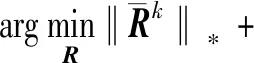
(22)

忽略式(22)中常数项，可以进一步表示为

(23)

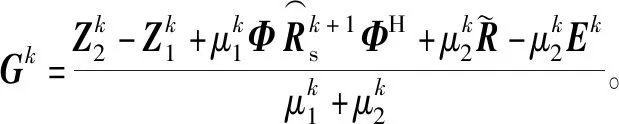
(24)

式中：Uk和Vk分别是Hk的左奇异值和右奇异值向量，即Gk=UkΣk(Vk)H，其中Σk是由奇异值组成的对角矩阵。

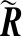
(25)

因此可得E的完整迭代解为

(26)

综上所述，式(11)所表示的优化模型的求解步骤总结如下：

1 while not converged do

4 while not converged do

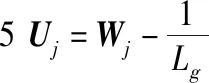
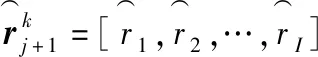
9j←j+1

10 end while

12 //Line 13～14迭代求解R子问题

15 //Line 16迭代求解E子问题

20k←k+1

22 end while

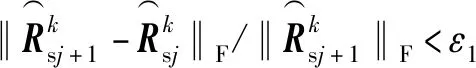
本文方法、文献[6]和文献[8]方法的计算量都是包括完整协方差矩阵重构和DOA估计算法两部分，计算量差异主要体现在完整协方差矩阵重构，如表1所示，其中K2表示循环迭代次数。

表1 计算复杂度比较

3 仿真结果及分析

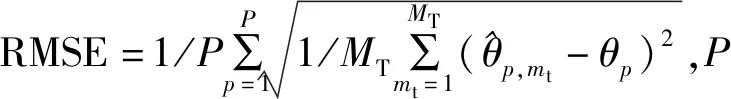
3.1 本文方法DOA估计误差随网格划分个数的关系

本实验选取的角度搜索空域为[-90°,90°]，对应等正弦空间稀疏化方式的搜索空域为[-1,1]。假设MIMO雷达发射阵列中第3个阵元失效，接收阵列中第3,5,7,10,14个阵元失效，信噪比为-10 dB，快拍数为100。由图1可知，在相同的网格数下，相对于等角度空间稀疏化方式，等正弦空间稀疏化方式的DOA估计性能更优；随着网格数的不断增加，两种稀疏化方式的DOA估计性能总体上变优，当网格数大于101时，DOA估计精度几乎不变，即构建字典时网格划分无需非常精细，采用粗网格划分空间方式的DOA估计性能几乎达到细网格划分时相比拟的性能。下面仿真实验均采用等正弦空间稀疏化方式构建字典，且网格数为201，对应的等正弦划分间隔0.01。

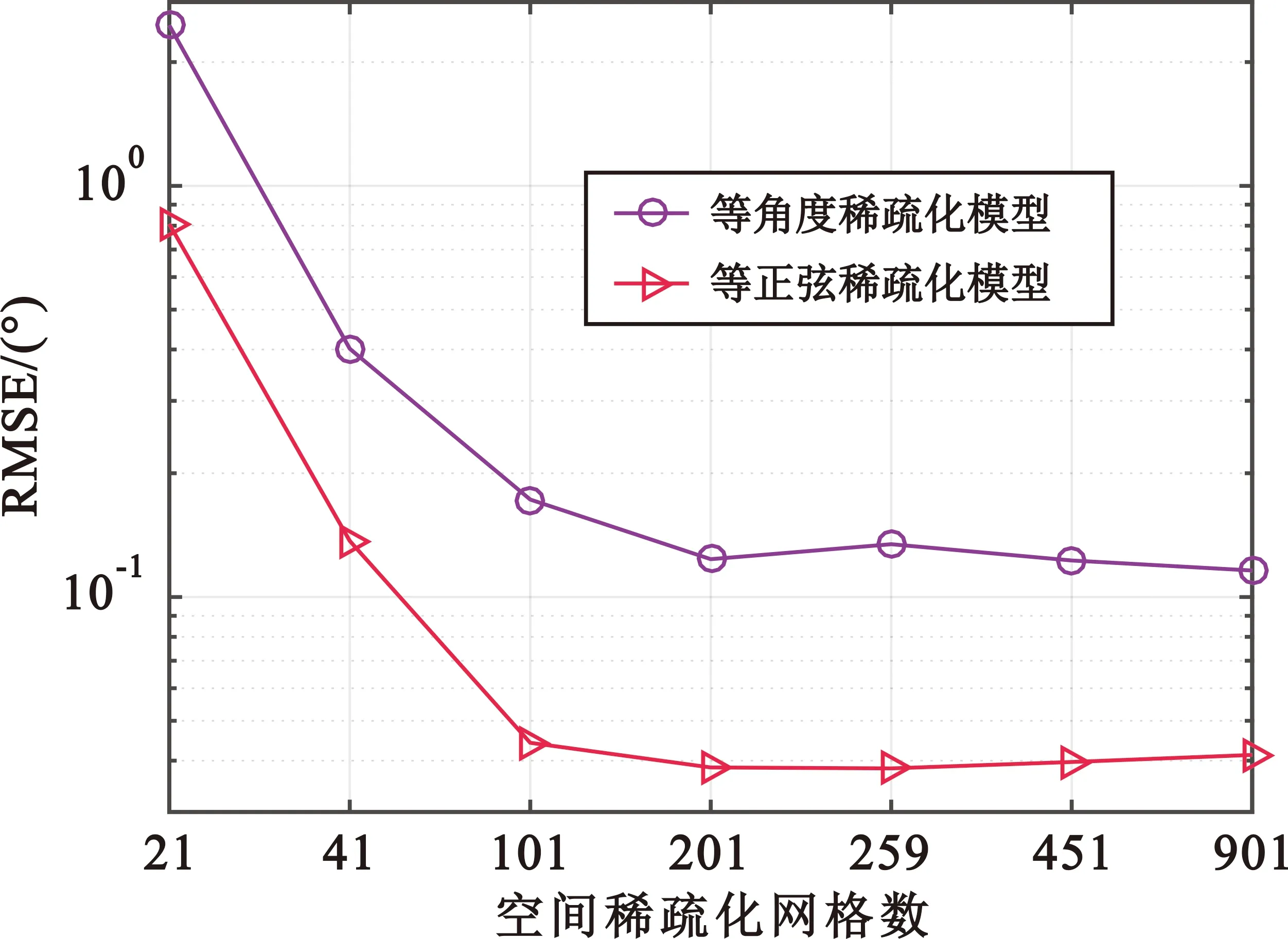
图1 DOA估计RMSE随空间稀疏化网格数变化

3.2 不同方法DOA估计误差随信噪比变化关系

本实验设置信噪比的变化范围为-30～0 dB，其余仿真参数不变。从图2可知，阵元失效破坏阵列协方差矩阵数据结构的完整性，因此直接采用RD-ESPRIT算法无法有效估计目标的角度；文献[6]和文献[8]方法在重构完整协方差矩阵时只利用了矩阵的低秩特性，而本文方法使用SCAD惩罚，提供足够的正则化来弥补低秩先验信息的不足，因此DOA精度明显更优，且低信噪比时精度高于阵元正常的DOA估计精度。

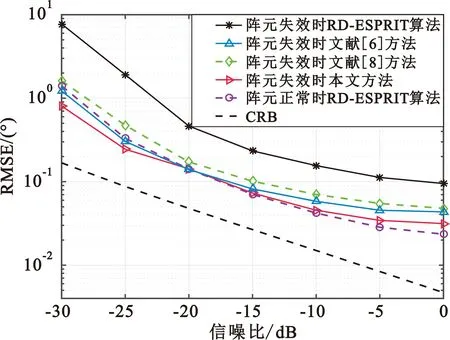
图2 DOA估计RMSE随信噪比变化

3.3 不同方法DOA估计误差随快拍数的变化关系

本实验设置快拍数的变化范围为50～350，信噪比为-15 dB，其余仿真参数不变。从图3可知，直接采用RD-ESPRIT算法时，阵元失效下的DOA估计误差始终大于与阵元正常时DOA估计误差；随着快拍数的不断增加，所有方法的DOA估计性能均有所提升，本文方法始终优于文献[6]和文献[8]的方法，且DOA估计精度接近阵元正常时采用RD-ESPRIT算法的DOA估计精度。

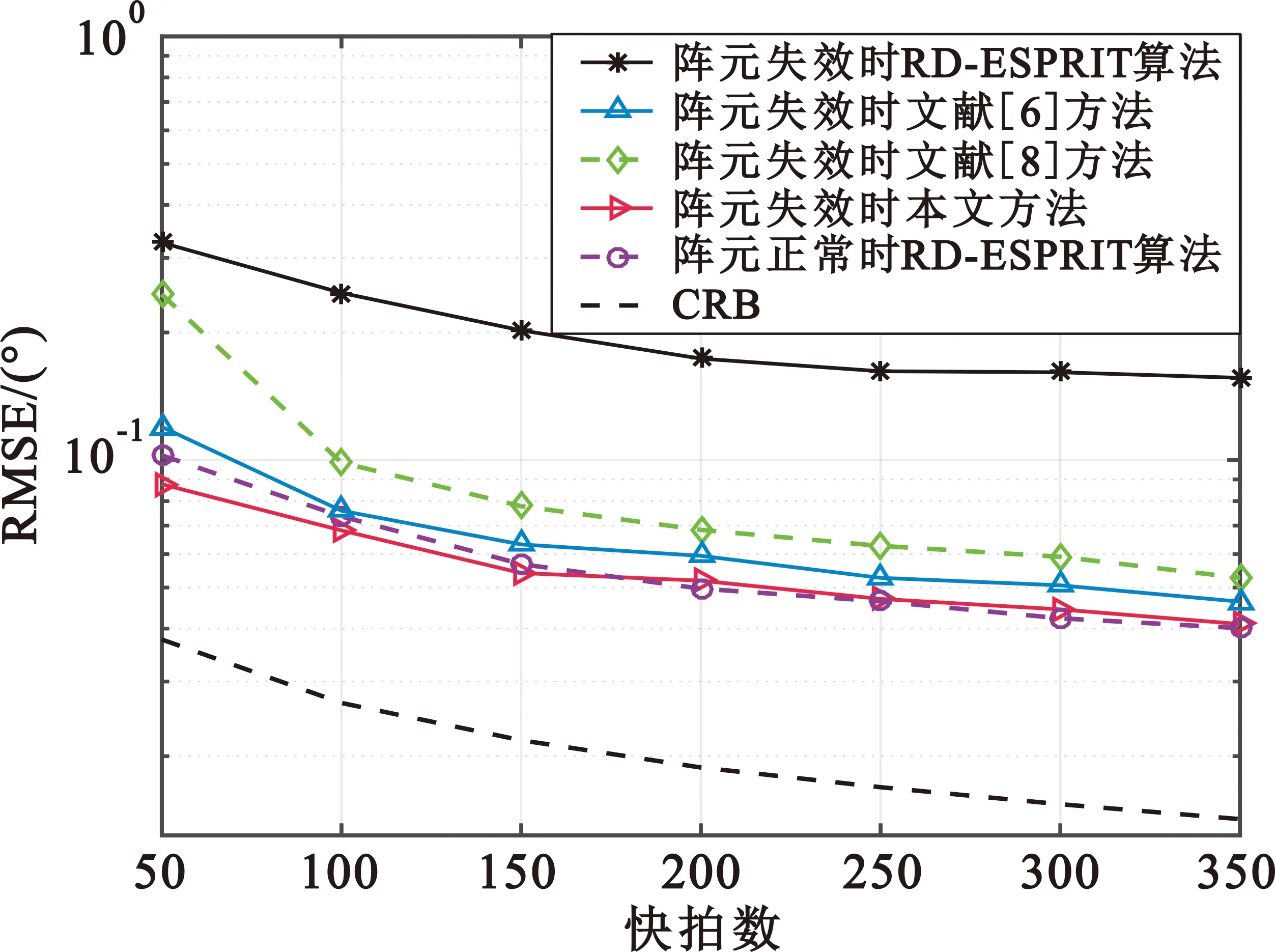
图3 DOA估计RMSE随快拍数变化

3.4 不同方法DOA估计误差随失效阵元数的变化关系

假设MIMO雷达发射阵列中第3个阵元失效，接收阵列中失效阵元数由1～9增加，每次接收阵列中失效阵元的位置均随机变化，设置信噪比为-15 dB，其余仿真参数不变。由图4可知，随着失效阵元数的增加，各方法的DOA估计性能均有不同程度的下降，但本文方法的目标DOA估计性能始终优于文献[6]和文献[8]的方法，即本文方法在恢复阵列协方差矩阵中缺失数据时稳定性更好，对失效阵元个数具有较好的鲁棒性。

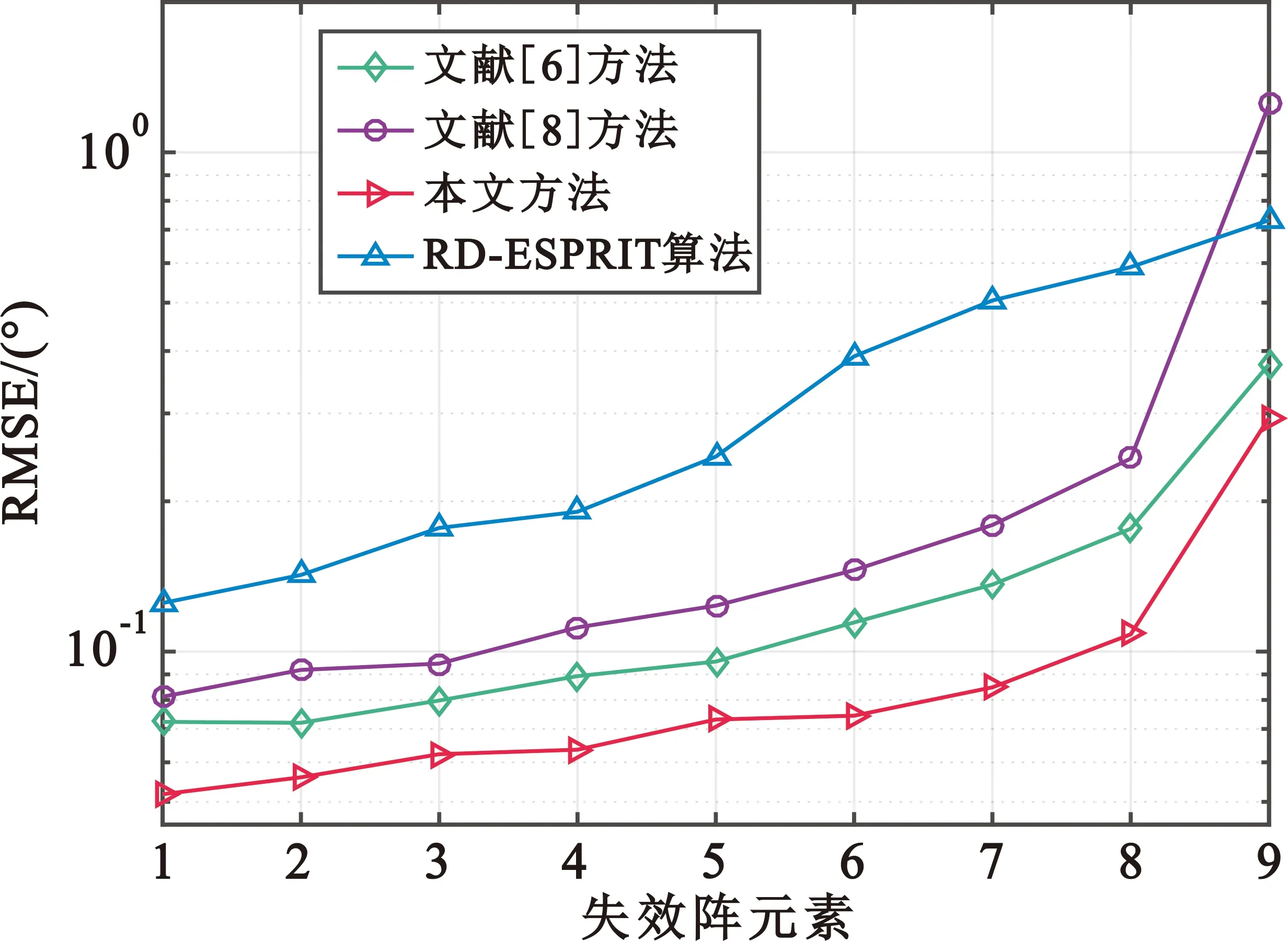
图4 目标DOA估计RMSE随失效阵元数变化

3.5 不同方法运行时间对比

本实验设置信噪比为-15 dB，运行软件为MATLAB2018a，CPU为Intel(R)Core(TM)i7-8750H，主频为2.2 GHz，内存为8 GB，其余参数保持不变。由表2可知，相比于文献[6]和文献[8]方法，本文方法运行时间更短，同时DOA估计性能更优。

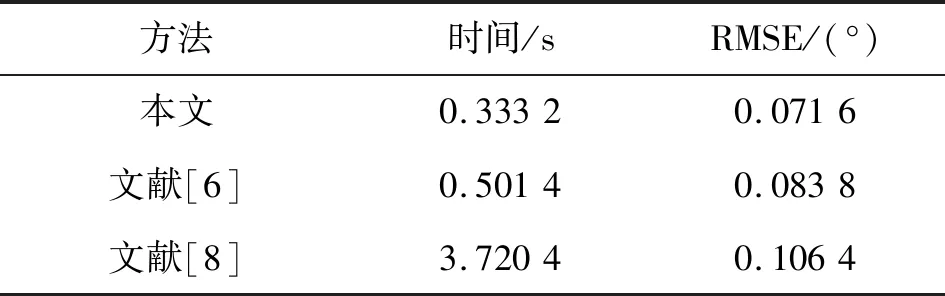
表2 不同DOA估计方法的运行时间

4 结 论

阵元失效下MIMO雷达虚拟阵列协方差矩阵会出现大量整行整列缺失元素，致使DOA估计性能恶化甚至完全失效。针对此问题，本文对待恢复的协方差矩阵建立核范数和SCAD惩罚联合约束模型，并采用等正弦空间稀疏化方式构建字典，确保在粗网格划分下字典产生的模型误差对缺失数据恢复不灵敏，同时能降低运算复杂度；然后利用ALM-ADMM算法求解双先验约束模型，从而恢复MIMO雷达协方差矩阵中因阵元失效而导致的大量整行整列缺失数据。本文方法能快速恢复阵元失效下协方差中的缺失数据，有效避免因失效阵元而导致DOA估计性能下降的问题。