毫米波星间通信测距一体化技术研究*

张仲楷，崔高峰，和梦敏，辛 星，王卫东

(北京邮电大学 电子工程学院，北京 100876)

0 引 言

卫星星间链路(Inter-Satellite-Link，ISL)是指在卫星或者是航天器之间建立的无线链路，借助该链路便可以完成星间数据通信以及距离测量。根据使用频段，星间链路主要分为微波/毫米波链路以及光学链路。光学链路有着通信带宽大、传输速率快以及测距精度高等优点，但其波束较窄，难以对准、跟踪、捕获[1]。而相较于微波链路，毫米波星间链路具有传输速率高、频谱资源丰富等特点。目前星间链路主流的频段为Ka频段[2]，而随着通信技术的不断发展，更多的目光投向了Q和V频段。该频段具有更加丰富的频谱资源，具有良好的发展和应用前景，是未来研究的重点。对于小卫星编队，使用毫米波星间链路可以提升传输效率同时扩展频谱资源，而星间链路中的传播时延以及多普勒频率偏移也对信号处理技术的性能提出了一定的要求。

在目前的毫米波星间链路中，星间通信和星间测距相对比较独立，通常需要两套系统分别实现。如果设计一种一体化波形，将通信和测距整合到一个系统，便可以实现星间通信测距一体化，有利于减小卫星的负载以及系统开销，符合卫星小型化的发展趋势。目前主要用到的一体化波形为“GMSK+PN”,即将数据进行GMSK调制再叠加上负责测距的PN伪码序列。文献[3]使用了“GMSK+PN”技术用于X频段星地链路的通信测距一体化，文献[4]则用于星间链路的通信测距一体化，而文献[5]则应用于深空通信中的测量数据返回以及轨道距离的确定。将通信波形和测距波形相叠加势必会对通信波形带来一定的干扰，进而影响系统的通信性能。所以如何利用一定的信号处理技术消除波形叠加对通信性能的影响，成为通信测距一体化的关键。此外，由于波形的叠加会导致信号拥有比较高的峰均功率比(Peak-to-Average Power Ratio,PAPR)，此时通过星载功率放大器会给信号带来非线性失真。功率放大器具有一定的非线性特性，所以不可避免会给输入信号带来幅度和相位畸变，导致信号产生非线性失真，从而影响系统的性能。传统的星载功率放大器的线性化技术包括功率回退法、前馈法、反馈法、包络跟踪技术以及预失真技术，这些技术都能在一定程度上消除非线性的影响。而针对于毫米波功率放大器的线性化器的研究起步较晚，目前还在发展阶段。

针对上述两项影响因素，需要提出相应的技术来提高一体化系统的通信性能。而近些年来，各种人工智能(Artificial Intelligence，AI)技术被运用于多个领域，所以相关研究人员也逐步把包括深度学习(Deep Learning，DL)在内的多种AI技术与通信系统相结合以达到更好的性能，例如将深度神经网络(Deep Neural Network，DNN)用于物理层(Physical Layer，PHY)的信号处理。文献[6]针对多径信道下的正交频分复用(Orthogonal Frequency-Division Multiplexing，OFDM)信号，使用DNN对无线信道特性进行学习，从而恢复出正确的比特数据。由于毫米波波段的信号具有高信号衰减这一缺点，需要使用波束赋形技术进行弥补，这同时也对信道估计和追踪技术提出了很高的要求。文献[7]使用了DNN进行信道估计，然后使用了长期依赖记忆网络(Long Short Term Memory Network,LTSM)实现了对信道状态的实时追踪。对于上述文献，深度学习均在一定程度上提升了通信系统的性能，证明了深度学习与通信物理层结合的研究价值。

本文针对卫星毫米波星间链路，提出了一种一体化波形，将通信测距两项功能整合到一套系统中去；并针对该波形提出了一系列信号处理算法，实现了通信数据的解调以及星间距离的解算。此外，提出了一种基于深度学习的信号检测算法，消除了波形分离以及功率放大器非线性带来的影响，减小了通信数据的误比特率(Bit Error Rate,BER)，提高了系统的性能。

1 星间链路

构建星间链路需要着重考虑载波频段选择问题。对于传统的卫星通信来说，云衰、雨衰、大气吸收以及路径损耗是影响使用频段的主要因素。载波频率越高，信号受到损耗、衰落越大，这就对星地毫米波通信带来了一定的制约。而星间链路的场景不存在上述制约因素，可以采用Ka甚至更高的Q/V毫米波频段。根据文献[8]，本文采用了比较典型的异面同绕飞中心的卫星构型，即辅星围绕主星的绕飞轨道不在一个平面，但是拥有同一个绕飞中心且具有相同的绕飞半径，绕飞半径为30 km，主星以及辅星的轨道六根数如表1所示；在载波频段方面，本文采用了V频段(约60 GHz)。利用STK(Satellite Tool Kit)仿真软件，根据上述参数建立主星和辅星间的星间链路，且分析星间链路的各项参数，最大多普勒频率偏移为2 kHz。为了保障通信测距一体化系统的性能，需要一定的信号处理技术实现精准的时频同步以及信道估计。

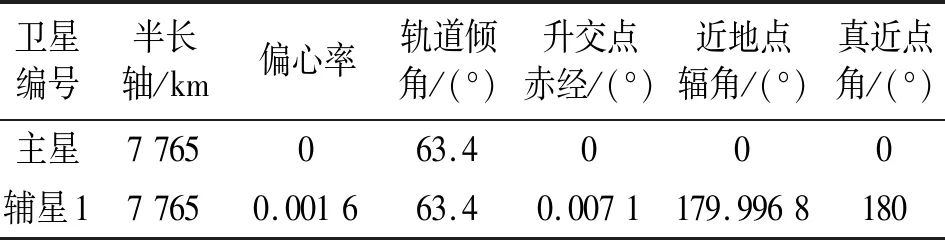
表1 卫星轨道六根数

除此之外，功率放大器的非线性特性也是影响系统整体性能的因素。目前毫米波星载功率放大器通常采用行波管放大器(Traveling Wave Tube Amplifier,TWTA)，本文采用了Saleh提出的TWTA非线性模型[9]，式(1)和式(2)分别代表了该功放模型的幅度特性(AM/AM)以及相位特性(AM/PM)。

(1)

(2)

式中：r表示输入信号幅度；αa、βa、αφ、βφ四个参数大小决定了模型幅度以及相位特性。参考文献[9]，功放模型的参数设置为：αa=2.158 7，βa=1.151 7，αφ=4.003 3，βφ=9.104 0。

2 系统模型

2.1 波形结构

通信测距一体化波形结构如图1所示，将等符号速率的通信波形和通信波形叠加，产生一体化波形，再进行后续的过采样以及成形滤波得到一帧数据。

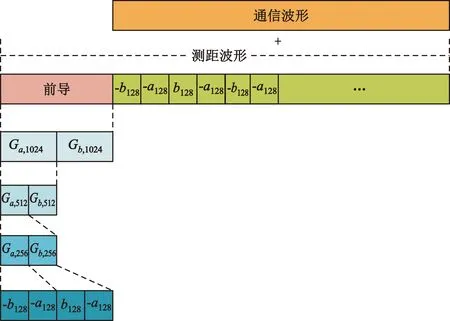
图1 波形结构图

测距波形由格雷互补序列对构成。格雷序列是指一对具有一定长度且具有良好的自相关性的序列。若定义一个序列a(n)的周期自相关函数为

(3)

则一对二进制格雷互补序列具有以下的性质：

(4)

当一对长度为N的二进制序列满足公式(4)所示的特性时，该序列对为长度为N的格雷互补序列。若将长度为N格雷互补序列对记为Gα,N、Gβ,N，而它们的二进制反码序列记为-Gα,N、-Gβ,N，把该序列对作为基序列对的话，则根据公式(5)可生成的长度为2N序列对依旧满足公式(4)，具有良好的自相关性质。

(5)

按照公式(5)依次类推，则长度为M(M=2KN)的格雷互补序列对可以由基序列推导K次得到。如图1所示，本文测距波形采用的基序列为长度为64的格雷互补序列对,由此得到长度为128的Gα,128、Gβ,128，简记为a128和b128。根据公式(5)，再由a128和b128可以推导出更长的格雷互补序列。而整个测距波形就是由一对长度为8 192的格雷互补序列构成，表达式为

r(n)=[Gα,8192,Gβ,8192]=Gα,16384。

(6)

式中：r(n)为测距波形，规定测距波形头部2 048位为通信前导(Comm Preamble，CP)。由于CP本身也是格雷序列构成，拥有着良好的自相关性能，可以用于进行时频头部以及信道估计，表达式如(7)所示：

p(n)=[Gα,1024,Gβ,1024]=Gα,2048。

(7)

通信波形由数据比特经过正交相移键控(Quadrature Phase-shift Keying，QPSK)生成，然后和相同符号间隔的测距波形叠加生成一体化波形。由于测距波形比通信波形长了一个CP，所以在通信波形的头部要补上2 048个0。

2.2 信号模型

通信测距一体化系统的框图如图2所示。

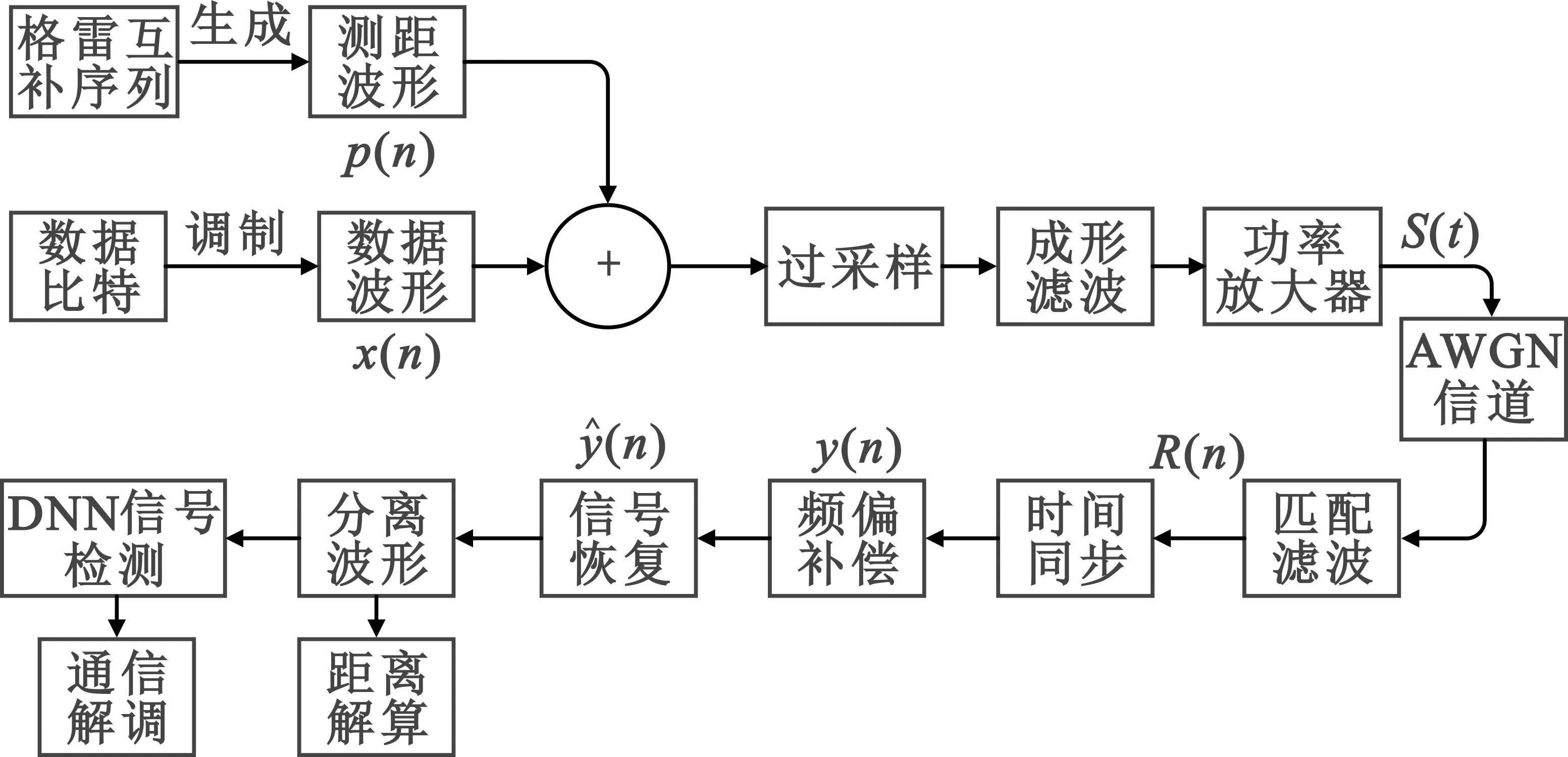
图2 系统框图

若一体化波形符号间隔为Ts，在经过过采样后采样周期为Ts′=δTs，其中δ代表了过采样倍数，则经过成形滤波器后信号可表示为

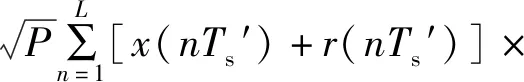
g(t-nTs′)ej2πfct。

(8)

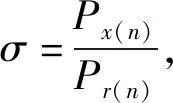
之后信号经过功率放大器以及信道，会受到环境噪声、传播时延以及多普勒频移的影响，接收信号Rc(t)可表示为

Rc(t)=S(t)ej2πfcτej2πfdopplert+n(t)。

(9)

式中：τ代表了系统的传输时延；fdoppler代表了相对运动带来的多普勒频率偏移；n(t)代表了加性高斯白噪声。而接收信号在经过降采样以及匹配滤波之后得到离散信号R(n)为

(10)

2.3 时间同步

星间链路中的传播时延以及卫星间时钟不同步都会影响正确接收信号，所以需要完成时间同步，寻找信号的最佳采样时刻。由于CP序列由长度为2 048的格雷互补序列对构成，所以对接收信号和本地CP序列进行移位相关，相关值Rp(k)如公式(11)所示：

(11)

2.4 频偏估计

(12)

(13)

利用频偏估计得到的多普勒频移对接收序列进行频偏补偿，公式(14)中y(n)为经过时频同步处理后的信号，

(14)

(15)

式中：N为一个CP序列长度即2 048。可见频偏估计的范围和系统的基带符号速率是呈正相关。

2.5 信道估计

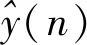
(16)

(17)

2.6 波形分离

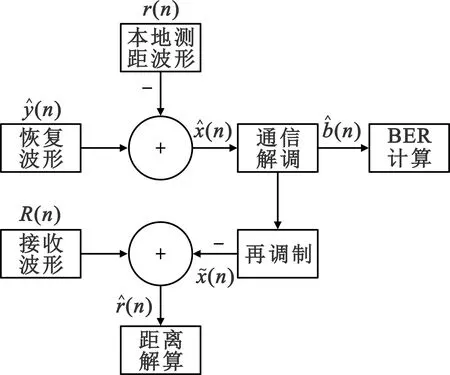
图3 波形分离流程图

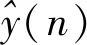
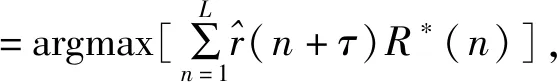
(18)

range=ϑ×c×Ts(0≤ϑ<16384)。

(19)

式中：L表示叠加波形同时也是测距波形的长度；τ表示滑动相关器的时延；Ts代表测距波形周期；c是光速。当ϑ取得最大值16 384时，测距结果为最大无模糊距离，所以测距范围和测距波形周期呈正相关，而测距波形一个采样点对应电磁波的传播距离cTs′为测距的最小误差值，则测距精度和测距波形周期呈负相关。

2.7 基于深度学习的信号检测

本系统采用的深度神经网络(Deep Neural Network)模型如图4所示，由输入层、隐藏层和输出层总共5层神经网络组成。

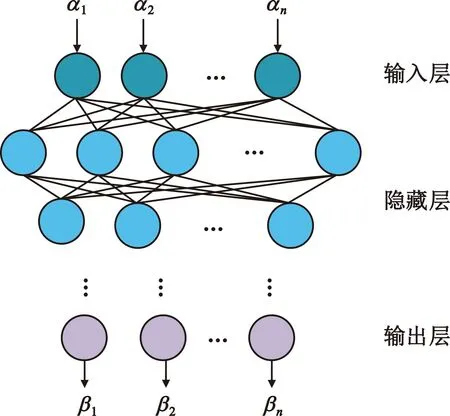
图4 深度神经网络结构

每层神经网络均包含多个神经元，采用全连接层进行连接，且对每层输出做批标准化(Batch Normalization，BN)。若输入层数据为α1,α2,…,αn，则对于隐藏层第L+1层的第n个神经元，输出βn可表示为

(20)

式中：wi代表神经元的权重；bi代表偏置；f(L)表示了第L层的激活函数。激活函数为非线性函数，能够增加网络的表达能力，而本网络用到的激活函数公式如下：

fRelu=max(0,x)，

(21)

(22)

神经网络前四层采用了Relu激活函数，输出层采用Tanh函数，优化器选用了Adam优化算法，目的是为了在提高神经网络的表达能力的基础上减少网络收敛所需要的时间，以达到最佳的网络性能。

对于存在的基于深度神经网络的信号检测算法训练流程如图5所示。数据比特产生发送信号，再经过信道以及接收端的信号处理后进行波形分离，此时分离后的信号包含着残存的测距波形以及功率放大器带来的非线性失真。将数据投喂给网络模型进行训练，从而让网络学习到分离波形残余干扰以及功放非线性特性，恢复出正确数据比特。

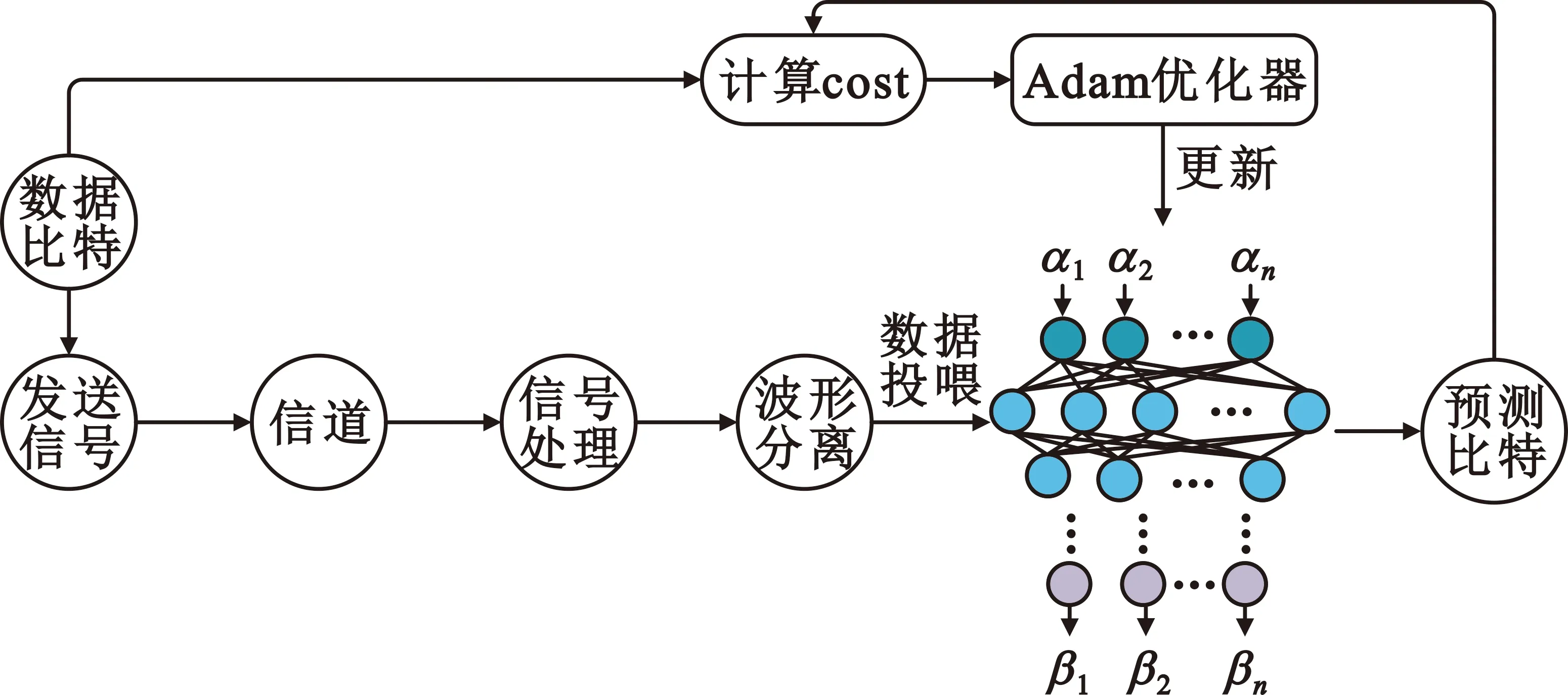
图5 信号检测算法框图

本文使用了离线训练、在线优化的策略，预先使用一定信噪比下的数据进行网络的训练。针对于不同场景，需要将预先训练的网络进行再优化，以达到适应不同环境条件的目的，体现出深度神经网络的泛用性。此外，为了确保网络模型预测的准确度，在线部署时采用网络并行的方式，每个网络的输入和结构都一模一样，每次输入64个符号的实部和虚部，即128个输入数据，而网络每次的输出为32个比特。采用的网络参数如表2所示。

表2 神经网络参数

为了方便算法的描述，首先定义以下变量：Sm为每个样本中的第m个复值符号；Im为第m个复值符号的同相分量；Qm为第m个复值符号的正交分量；batch为神经网络的超参数，表示从数据集上划分的一批数据样本；epoch为神经网络的超参数，表示网络在数据集上循环的次数；L为损失函数，采用均方误差函数；li为样本标签里的第i个目标变量；pi为第i个预测值。算法流程如下：

Step1 初始化神经网络训练参数。

Step2 数据预处理：

Step2.1 将接收信号进行时频同步、信道估计、波形分离等信号处理得到通信波形的IQ数据；

Step2.2 每64个复值符号组成一个样本，分别取出符号的同相以及正交分量Im和Qm；

Step2.3 按照同相分量在前，正交分量在后的顺序排列输入数据，得到一个样本(Sample)数据[I1,I2,…,I64,Q1,Q2,…,Q64]。标签(label)为对应的32 b数据；

Step2.4 采集并处理样本和标签，并划分为训练集(Training set)、验证集(Validation set)以及测试集(Test set)。训练集以及验证集数据为信噪比。

Step3 利用数据集进行网络训练：

Step3.1 将训练集数据样本通过输入层输入到神经网络当中；

Step3.2 根据当前隐藏层网络参数以及激活函数计算逐层输出，并且每个隐藏层在输出之前做批标准化处理；

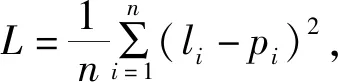
Step3.4 重复Step 3.3直到遍历完整个数据集，即运行了一个epoch，将验证集的数据输入进行模型精度的验证；

Step3.5 重复Step 3.3及Step 3.4直到在数据集上完成epochs次迭代。

Step4 在测试集上进行测试。对于采用不同σ的测试集进行微调(fine-tuning),再对不同信噪比下的测试集进行测试。

3 仿真结果及分析

为了验证本文提出的一体化波形以及信号处理算法的性能，将利用Matlab2020a以及Python3.6进行仿真分析。分别对理想功率放大器以及TWTA的Saleh模型下的系统进行仿真，系统参数配置如表3所示。根据2.6节可以得到系统的最大无模糊测距范围约为240 km，测距精度达到分米级，同时提供了40 MHz的通信速率。同时根据式(15)，通过CP进行频偏估计，估计上限约为9.765 kHz，满足前文中星间链路的参数，同时测距范围也满足一般小卫星编队相对距离的范围。

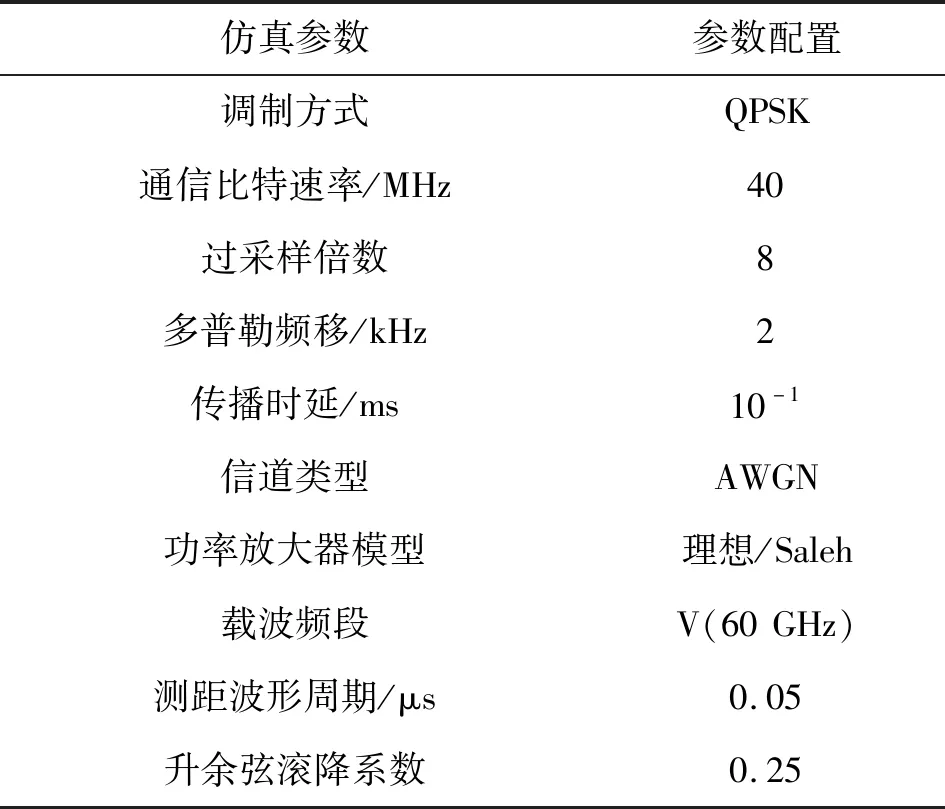
表3 系统仿真参数

对于基于DNN的信号检测算法部分，分别对不同功率占比的一体化波形信号进行仿真。首先分别采集了各100 000组SNR=16 dB时的数据作为训练集，其中又划分出15 000组数据作为网络训练的验证集。训练时优化算法为Adam算法，学习率设为0.001。神经网络的前2 000次损失函数值如图6所示，损失函数随着训练的进程不断处于下降趋势。在2 000个epoch的时候，网络对验证集数据的预测性能基本趋于收敛。利用预训练好的网络可以对不同信噪比下的数据进行测试，从而分析网络的性能。在线部署阶段，为了保证网络的预测性能，可以进行在线微调，根据应用场景实时更新网络参数。

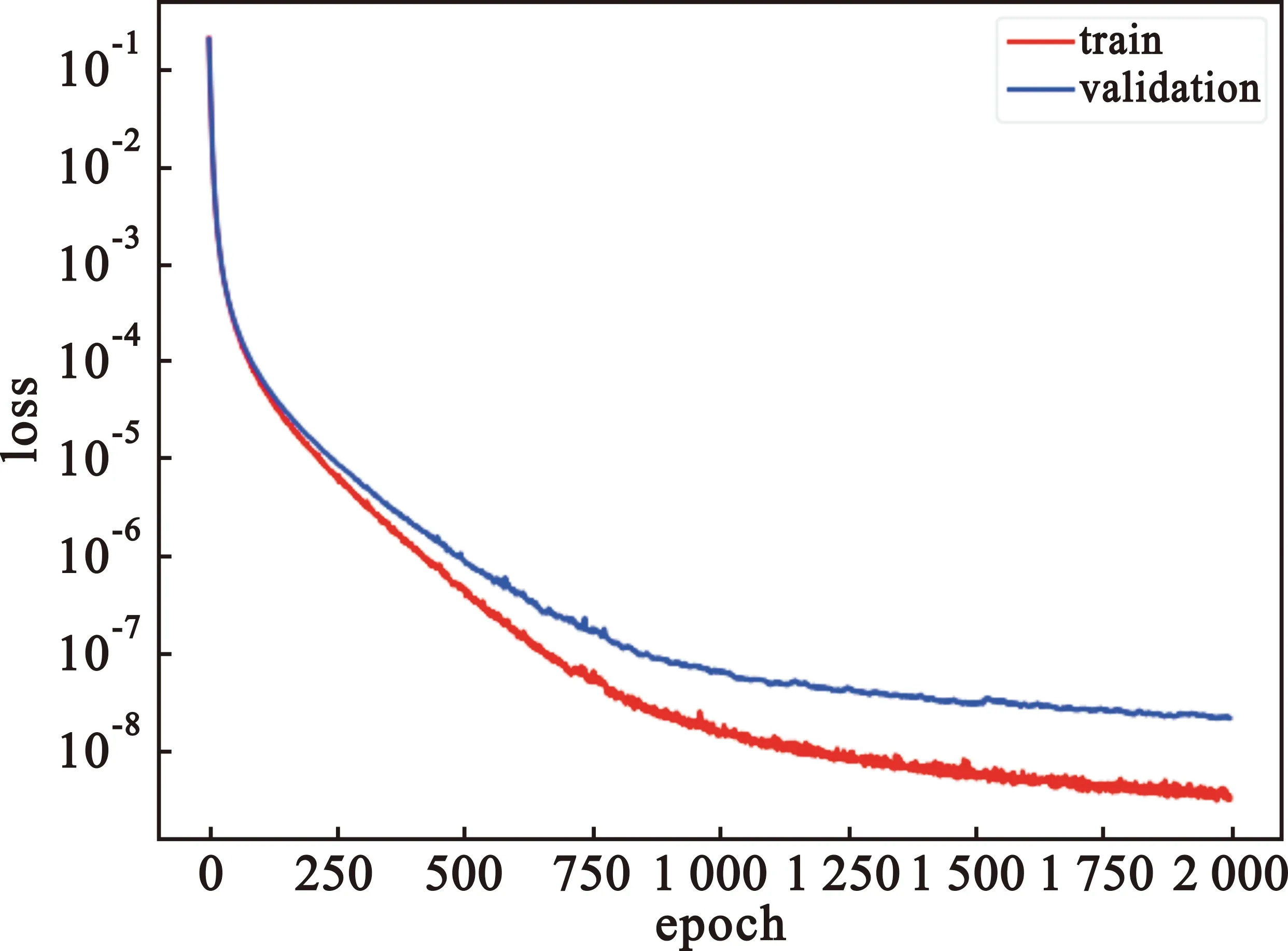
图6 神经网络损失函数图

对于通信解调，由于当通信波形与测距波形按相同功率进行叠加即σ=1时，理想功放和Saleh模型下的仿真结果如图7所示。经过信号处理，当SNR>16 dB时，误比特率达到了10-6；使用了基于DNN的信号检测算法之后，性能能够提升大约2 dB，且当SNR>12时，误比特率达到0，可见本文提出的算法可以消除分离波形带来的影响，明显提升了系统的性能。当使用Saleh模型之后，系统的误比特率急剧降低，当SNR>16 dB时误比特率只达到了10-4，而在使用了基于DNN的信号检测算法之后能达到10-5，说明了本文提出的算法在Saleh模型下可以有效抵抗功放非线性失真，提高系统的性能。

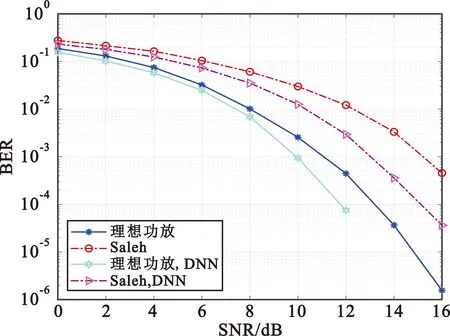
图7 σ=1下理想条件与Saleh模型的对比

对于理想功放条件下，叠加功率比即σ的取值对通信解调的BER有着比较大的影响。图8为理想功放条件下三种σ取值的一体化波形在不同信噪比下的误比特率图，可见不使用DNN信号检测算法的情况下，随着σ的增大，测距波形在一体化波形中的占比降低，对通信波形的干扰也减小，所以BER会有着明显的降低。σ=1时，当SNR>16 dB，误比特率可以达到10-6；而σ=2和σ=3时，误比特率可以降到0，SNR>14 dB时，BER也分别达到了10-6和10-7。而使用了基于DNN的信号检测算法之后，性能明显得到一定的提升，当σ=1以及σ=2时，SNR>14 dB误比特率就降到0；σ=3时，SNR>10 dB误比特率就可以降到0。

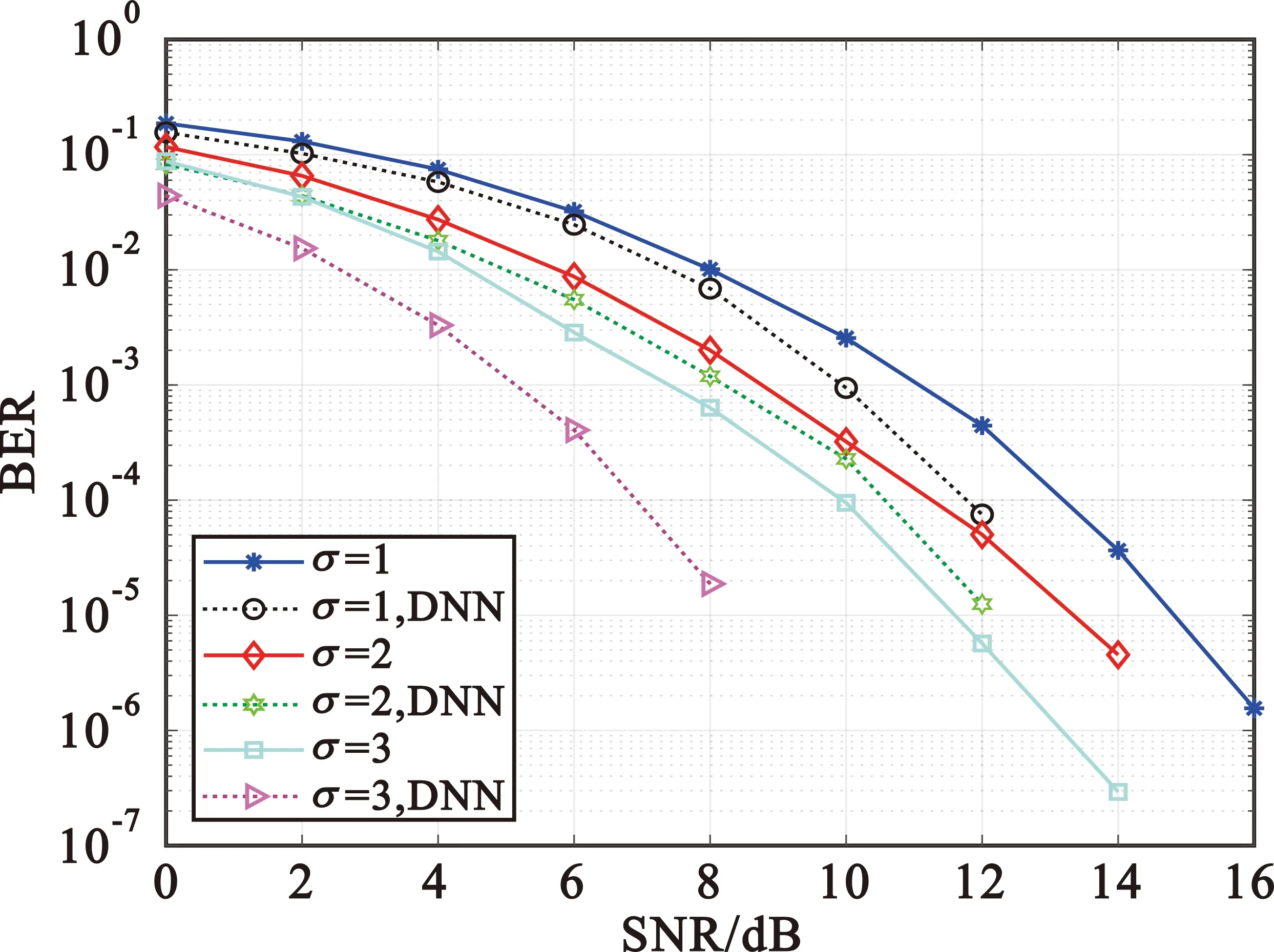
图8 理想功放条件下不同σ的对比

图9为Saleh模型下三种σ取值的一体化波形在不同信噪比下的误比特率图，可见在采用TWTA的Saleh模型后，随着σ的增大，BER在逐步降低。测距波形占比降低不但会减小对通信波形的干扰，还会降低一体化波形的PAPR，非线性失真程度也会降低，而使用基于DNN的信号检测算法明显提升了系统的性能。σ=1以及σ=2时，使用DNN信号检测算法使误比特率性能提升了大约2 dB，当SNR>16 dB，误比特率均达到了10-5；σ=3时，当SNR>14 dB，误比特率就达到了10-5，而当SNR>16 dB时，误比特率降到了0。可见在TWTA的Saleh模型下，DNN可以充分学习到功率放大器的非线性特性，恢复出正确的信号，从而提升系统的性能。

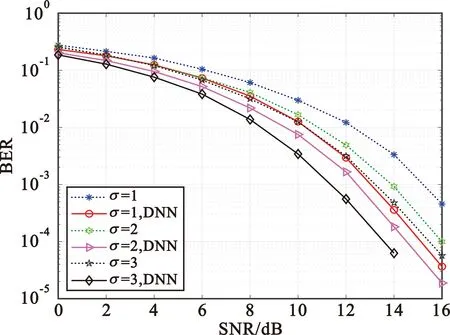
图9 Saleh模型下不同σ的对比

σ的取值不同对于系统的仿真性能有着较大的影响：在噪声以及多普勒频移的干扰下，分离测距波形会对通信的解调性能带来一定影响，测距波形功率占比越小，则系统的通信性能将越好，而对于星间测距，测距波形占比越大，则对距离精确测量所需要的信噪比越小。所以当信噪比较高时，可以提高σ即通信波形在叠加波形中的功率占比，以提升系统的通信性能。

4 结 论

本文针对卫星移动通信星间链路设计了一体化波形，并研究了对应的信号处理技术搭建了星间通信测距一体化系统；同时针对分离波形对通信波形的干扰以及功率放大器非线性特性给信号带来的失真，提出了基于深度学习的信号检测算法，并对理想条件和Saleh模型下的一体化系统进行仿真。仿真结果表明，在理想功放模型下，本文提出的算法能够消除一部分分离波形带来的干扰，降低通信解调的误比特率；在使用TWTA的Saleh模型下，本文提出的算法能够学习到功率放大器的非线性特性，降低非线性失真带来的影响，提升系统的性能。