基于支持向量机的斜拉桥悬臂施工挠度预测研究

曾丽华 ，王希瑞

(1.广西理工职业技术学院，广西 南宁 532200；2.广西交科集团有限公司，广西 南宁 530007)

0 引言

随着我国桥梁建设的发展，斜拉桥因其跨径大、造型美观和性能优越等特点得到了广泛的应用[1-2]。然而，由于斜拉桥刚度相对较小，在其悬臂施工过程中节段可能产生过大变形使得桥梁线形偏离设计值，甚至可能影响斜拉桥结构安全[3-5]。因此，为了保证斜拉桥悬臂施工的准确性，观测其施工阶段的挠度情况具有重要的意义。

关于斜拉桥挠度的研究，众多桥梁科研工作者进行了较为广泛的探索。郁光耀[6]结合有限元方法以及桥梁经验性数据，研究了混凝土收缩徐变对矮塔斜拉桥主梁挠度的影响规律；李惠成等[7]通过桥梁健康监测系统分析了季节温差和日照温差对预应力混凝土斜拉桥挠度的影响情况，分析得出季节温差是影响斜拉桥挠度变化的主要因素；潘宣亦[8]依托肇庆阅江大桥，采用Midas Civil软件进行有限元模拟分析，通过对施工阶段进行挠度验算，总结了斜拉桥施工中挠度测量及控制方法；刘小玲等[9]结合南京长江三桥监测数据，基于统计理论提出了斜拉桥主梁挠度的评估及动态预警方法，可有效保证桥梁正常运营；扈振涛等[10]通过有限元方法研究了混凝土容重、拉索张拉、施工荷载和收缩徐变对斜拉桥的影响规律，可为合理确定预拱度提供依据；刘扬等[11]基于虚拟中间变量法分析了支架材料、几何尺寸以及施工方案对斜拉桥主梁施工过程可靠度的影响，可为斜拉桥安全施工提供保证；梅秀道等[12]引入压力变送器连通管挠度系统对大跨斜拉桥进行挠度监测，分析表明该系统量程大、精度高并且稳定性好，适用于施工期主梁挠度监测；张豪等[13]基于卡尔曼滤波模型对大跨斜拉桥进行了挠度预测研究，分析表明该方法可较好地预测斜拉桥变形能力；随嘉乐等[14]结合灰色系统方法建立了矮塔斜拉桥悬臂施工的挠度预测模型并对其进行应用分析。从上述研究可以发现，现有关于斜拉桥的研究大多集中在挠度控制以及影响因素的分析方面，而对斜拉桥施工期间的挠度预测研究仍然涉及较少。虽然部分文献分别基于卡尔曼滤波和灰色系统方法对斜拉桥挠度预测进行了研究，但对于更高效简单的挠度预测应用方法仍有待进一步研究。近年来，支持向量机方法由于结构简单、训练速度快，并且具有较高的动态仿真能力等特点，广泛应用于工程结构的响应预测分析中[15-17]。若能通过支持向量机方法建立斜拉桥悬臂施工挠度预测模型，从而近似替代繁杂的现场挠度测量工作，将具有重要的科研意义和工程实用价值。

对此，本文基于支持向量机开展了斜拉桥悬臂施工挠度预测研究，以某典型工程的斜拉桥为例进行预测分析，并通过残差校核讨论本文方法预测结果的准确性，以期为斜拉桥悬臂施工挠度预测提供参考。

1 支持向量机基本原理

支持向量机(Support Vector Machine，SVM)是一种基于统计学习理论的机器学习算法，其预测精度较高[18-19]，适用于小样本分析。SVM理论上可以在全局意义上逼近任意非线性函数，具备良好的泛化能力，其结构如图1所示。

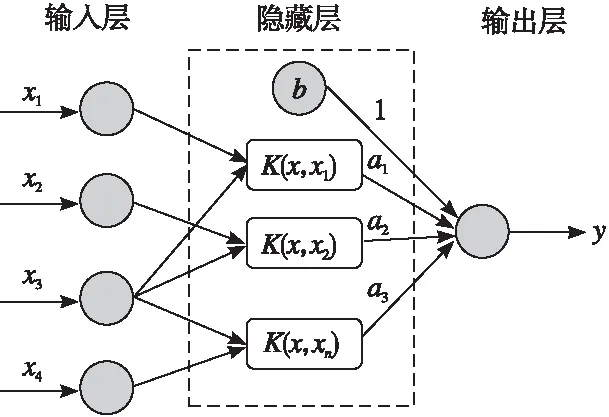
图1 支持向量机结构图

假设存在数据集A={(xi，yi)，i=1，2，…n}，则SVM拟合函数表达式为：

f(x)=wφ(x)+b

(1)

式中：w——权重系数向量；

b——常数；

φ(x)——映射函数。

w和b可通过风险函数得到，根据最小化风险原则，可得到结构风险函数Rsrm：

(2)

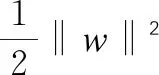
C——惩罚函数。

通过引入松弛变量ξi和ξi*，Rsrm的最小化可写成：

(3)

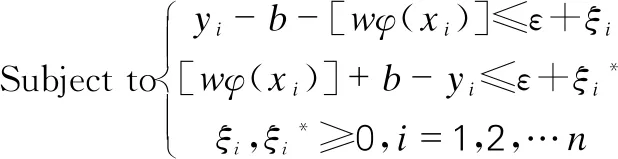
(4)

对于式(3)和式(4)，可通过Lagrange优化方法求解，对应有：

(5)

式中，ai和ai*表示第i个样本点对应的Lagrange乘子。

将式(5)代入式(1)，可得到函数f(x)：

(6)

式中，K(x，xi)表示核函数，其表达式为：

K(x，xi)=φ(xi)φ(xk)

(7)

2 基于支持向量机的斜拉桥挠度预测流程及步骤

通过斜拉桥有限元分析模型获得训练样本，结合支持向量机模型对输入样本进行网络训练，即可获得满足精度要求的斜拉桥挠度预测模型，进而可根据挠度预测结果进行残差校核。基于支持向量机的斜拉桥挠度预测流程如图2所示，实现步骤如下：

图2 基于支持向量机的斜拉桥挠度预测流程图

步骤1：结合有限元方法，建立斜拉桥有限元分析模型。

步骤2：分析斜拉桥运营过程的不确定性，选择主要因素作为样本向量，通过有限元模型计算样本点对应的挠度信息，确定训练样本。

步骤3：输入训练样本信息，基于支持向量机建立关系模型，直至斜拉桥挠度预测模型满足精度要求。

步骤4：根据斜拉桥挠度预测模型，进行相关挠度预测并分析该方法的有效性。

3 算例分析

3.1 斜拉桥有限元模型

为说明所提出方法的适用性，本文以典型工程斜拉桥为例进行分析，对其悬臂施工过程中竖向挠度进行预测研究。本文斜拉桥由三跨(110 m+220 m+110 m)组成，共有拉索40根，沿两侧呈对称分布。根据有限元软件ANSYS APDL模块建立斜拉桥有限元分析模型，斜拉索采用LINK10单元，该单元为三维仅受拉或受压杆单元；桥塔、主梁和横向系梁采用BEAM4单元，为承受拉压弯扭的单轴受力单元，适用于桥塔、主梁和横向系梁受力特性。材料选用方面，斜拉索的弹性模量、泊松比和密度分别为1.961 3×105MPa、0.30和7 698 kg/m3；桥塔弹性模量、泊松比和密度分别为2.745 9×104MPa、0.17和2 452 kg/m3；主梁和横向系梁弹性模量、泊松比和密度分别为2.059 4×105MPa、0.30和7 698 kg/m3。边界条件方面，通过节点约束的形式限制桥塔底部以及两侧横梁支座x、y、z方向位移，桥塔横梁和支座处设置弹簧约束，斜拉桥边界条件设置如图3所示。

(a)三维图

(b)正视图

3.2 挠度预测结果

基于上述分析，得到基于支持向量机的斜拉桥悬臂施工挠度预测结果。为了分析其预测的准确性，将有限元得到的挠度结果作为标准解进行对比分析，并以残差作为参数衡量指标，其中残差公式表示为：

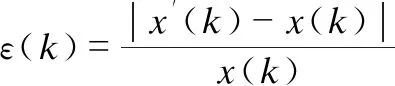
(8)

式中：ε(k)——第i个节段挠度残差；

x′(k)和x(k)——第i个节段挠度预测值和有限元挠度标准值。

参考文献[14]，当ε(k)<0.1时，认为本文预测结果达到较高的精度要求；当ε(k)<0.2时，则达到一般要求。

支持向量机的斜拉桥悬臂施工中7个节段的挠度预测信息及相应的残差结果如表1所示。由表1可知，斜拉桥挠度预测值同标准值残差指标ε(k)均<0.1，说明基于支持向量机模型方法能很好地预测斜拉桥悬臂施工挠度预测信息。斜拉桥节段-竖向挠度曲线如图4所示。由图4可知，挠度预测值和标准值曲线较为吻合，相对误差较小。随着节段号的增加，斜拉桥节段的挠度逐渐增加，这主要由于后续阶段逐渐趋于跨中，因此建议在斜拉桥施工过程中重点关注中间节段的挠度变化情况。此外，对比斜拉桥挠度预测值和标准值发现，挠度预测值始终相较于标准值有所偏高，从设计角度来看，预测值更偏于保守，因此施工过程中采用预测值进行分析是切实可行的。

表1 斜拉桥竖向挠度结果表

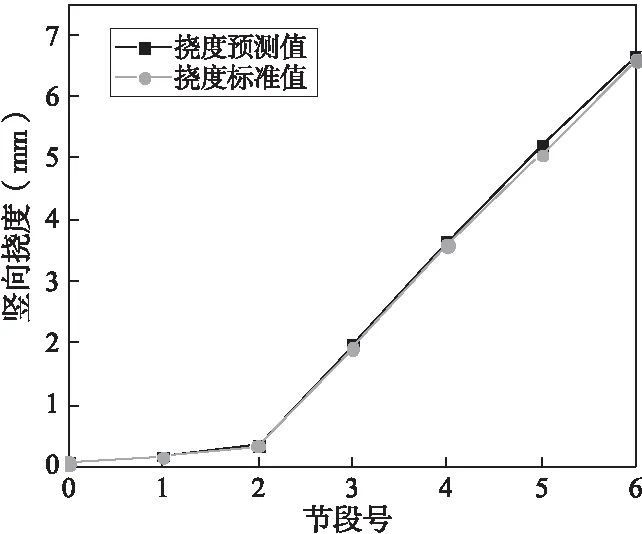
图4 节段-竖向挠度曲线图

4 结语

斜拉桥在悬臂施工过程中的挠度变化严重影响桥梁的线形质量，因此，本文基于支持向量机提出了斜拉桥悬臂施工的挠度预测模型，并以某斜拉桥典型实例验证所提方法的适用性，得出主要结论如下：

(1)基于支持向量机预测方法具有较高的精度，所预测的斜拉桥悬臂施工挠度结果同桥梁标准值残差<0.1，可应用于斜拉桥挠度预测。

(2)预测结果发现，跨中节段挠度整体大于边缘节段，建议在节段施工过程中重点关注跨中节段的影响。

(3)对比预测值和标准值发现，本文方法所得的预测值相较于标准值略有偏高，从设计角度考虑，采用预测值更偏于安全。