夹层玻璃PVE中间膜热流变行为及松弛特性

谢东东 ，杨健 ，王星尔 ，赵宸君

(1.上海交通大学 船舶海洋与建筑工程学院，上海，200240；2.上海交通大学 船舶海洋与建筑工程学院，上海市公共建筑和基础设施数字化运维重点实验室，上海，200240)

玻璃作为一种由硅酸钙构成的透明性材料，具有独特的美观性和广泛的市场应用。但玻璃力学性能上表现出脆性特征，耗能能力和延性较差，且开裂后会产生大量的玻璃碎片[1-2]，开裂后安全性欠佳。夹层玻璃由于高聚物中间膜的添加使得其表现出更好的延性、安全性和后破坏强度[3-4]，同时高聚物膜材也具有一定的隔音、隔热和过滤紫外辐射[5]等功能。如今夹层玻璃在建筑、汽车等行业应用越来越广泛。根据平板玻璃的全球市场轨迹与分析，全球平板玻璃在2020 年的市场估值为1 550 亿美元，到2027 年市场估值将达到2 833亿美元[6]。

目前国际上结构承载型的夹层玻璃被称为结构玻璃[7]，主要应用于楼梯、梁、板和墙等建筑结构构件。这类夹层玻璃大多采用热塑性高性能中间膜，典型代表有聚乙烯醇缩丁醛膜[8](PVB)、离子型中间膜[9](SG)以及乙烯-醋酸乙烯共聚物膜[10-11](EVA)。但这类膜材由于高聚物相对分子质量大，且同一高聚物中不同相对分子质量的分子链在外力作用下具有不同的平衡响应时间[12]，因此表现出明显的柔性和松弛特性。SERAFINAVIČIUS等[13]通过四点弯曲试验研究，指出PVB，SG 和EVA 三种膜材的夹层玻璃在长时间荷载作用下均会发生应力松弛现象。CENTELLES等[14]对多种膜材应力松弛的时间谱全貌进行研究，指出PVB，SG和EVA等膜材均具有时间敏感性，在长时间外力作用下模量会有一定程度的下降。常温下EVA膜材的时间敏感性处于PVB 膜材和SG 膜材之间，应力松弛模量在106s时刻开始骤降。BIOLZI等[15]基于时温等效原理对SG和PVB膜材的长期应力松弛特性进行研究，指出在20 ℃情况下SG 膜材在105s 时应力松弛模量已经下降至50 MPa，而PVB膜材下降更加剧烈至0.4 MPa。

此外，高聚物因内部分子的运动形式易受温度影响而表现出明显的温度敏感性。HOOPER等[16]研究表明PVB膜材具有温度和应变率敏感性，其在温度升高时出现玻璃态、黏弹态和橡胶态的逐次转变，力学性能在黏弹态发生急剧下降，并且拉伸刚度随着应变率下降而有所降低。徐晓庆[17]通过动态机械热力学试验指出SG膜材的玻璃转化温度区间为45～65 ℃，这使得在气候炎热的地区或季节SG 膜材会有高温软化现象。SCHUSTER 等[10]研究表明EVA 膜材在高温时模量已经跌至1.0 MPa 左右，抵抗外力的能力急剧下降，并且指出其具有时间-温度耦合敏感性，不遵从简单热流变行为规律。而膜材在夹层玻璃弹性阶段主要以传递剪力的形式协调上下层玻璃的变形，对夹层玻璃整体的承载能力作用显著。因此，夹层玻璃由于热塑性中间膜的作用在长期以及高温服役时会出现性能下降的现象。

改性EVA 膜材(PVE®)作为传统EVA 膜材的一种改性与提升，任明根等[18]通过单轴拉伸试验发现PVE与PVB、SG等膜材相似，其拉伸强度在常温以下维持较高水平，但在60 ℃以上力学性能均出现大幅度下降，表现出明显的温度敏感性。因此，PVE 膜材力学性能的温度相关性问题依然突出，同时EVA 膜材表现出的长时间松弛特性仍需保持关注。本文作者通过动态机械热力学试验(dynamic mechanical thermal analysis，简称DMTA)和蠕变试验对PVE 膜材的热流变行为和松弛特性开展研究。

1 试验概况

1.1 试验试件

DMTA 试验以及蠕变试验的试验样本均由橡胶冲片机对成片PVE 膜材进行冲裁制成，成片膜材以及冲裁样本均置于密封袋和锡箔纸中保存。PVE膜材的名义厚度为1.52 mm，试验样本的尺寸参考ISO 6721-1[19]和GB/T 11546.1—2008[20]以及试验仪器的现实条件进行制作。其中DMTA 试验样本长×宽为20 mm×7 mm，蠕变试验样本长×宽为15 mm×3 mm，且在试验时利用游标卡尺对试验样本的宽度和厚度重新测量，保证试验的准确性。

1.2 试验装置

两种试验均采用美国TA 公司的Q850 仪器。该仪器采用无摩擦、低柔量的空气轴承设计，确保卓越的力灵敏度和精确度，控制力的精确度为0.000 1 N；同时采用光学编码技术实现优质的分辨率，形变控制精度达到0.1 nm。高聚物长条形试样与两端夹具、连杆、应力传感器和位移传感器相连，在试验过程中测量试样的夹持长度以及所受的荷载。此外，该仪器配有空气压缩机和加热炉精准控制试验温度。Q850 仪器关键的技术参数见表1。

表1 Q850仪器关键技术参数Table 1 Key technical parameters of Q850 instrument

1.3 加载制度

DMTA 试验与蠕变试验的加载制度由于试验原理的不同而有所区别，DMTA 试验对膜材施加动态的交变荷载作用，而蠕变试验对试件施加恒定的应力水平，分别探究PVE 膜材的热流变行为以及长期松弛特性。

在本文中，DMTA试验根据ISO 6720-1考虑不同的温度和频率对膜材动态性能的影响。其中温度设定为-50～120 ℃，温度梯度为5 ℃；频率范围为0.1～10.0 Hz，频率梯度取对数增量，为0.1，0.2，0.4，0.8，1.0，2.0，4.0，8.0 和10.0 Hz。试验样本从-50 ℃以5 ℃温度梯度升高至120 ℃，当温度升至指定试验温度的±0.1 ℃时，恒温保温5 min，保证试验样本的温度与加热炉中的温度相同，避免膜材中热滞后效应的产生。热平衡后施加交变作用，最大振幅设定为10 μm；在此过程中由传感器测量试验样本的夹持长度以及外力荷载。

蠕变试验根据ASTM D2990—17[21]考虑不同的温度和应力水平对膜材长期松弛特性的影响。温度范围取-40～80 ℃，梯度为40 ℃；应力水平选取0.5 MPa 和1.0 MPa；蠕变时间设定为6 000 s。试验中先控制试验样本的温度至试验温度并恒温5 min，其次施加指定的应力水平并保持6 000 s。试验仪器内部先进的电机控制系统能够在50 ms内施加指定的应力水平，并同时记录此时试验样本的长度，数据点的采集频率为3 Hz。

2 试验结果及分析

2.1 PVE膜材热流变行为研究

交变荷载作用于PVE 膜材，膜材的黏弹性特征使得应力与应变之间存在0°～90°的相位差δ，其响应状态介于虎克弹性体与牛顿流体之间。因此，用损耗模量E″和储能模量E′分别表示膜材中的黏性成分与弹性成分，两者的比值被定义为损耗因子tanδ，用来衡量膜材的力学阻尼。

在DMTA 试验中，通过储能模量E′、损耗模量E″以及损耗因子tanδ三者反映膜材的性能变化，以此对PVE 膜材的热流变行为开展详细的研究，主要阐述不同温度区间膜材内部分子的运动形式、影响膜材的温度和时间两大因素的相关性以及膜材宏观表现出的黏弹性三方面内容。

2.1.1 松弛转变行为规律

PVE 膜材储能模量、损耗模量以及损耗因子随温度的变化曲线如图1 所示。从图1 可知：以10 Hz 频率交变荷载作用为例，PVE 膜材从-50 ℃升温至120 ℃主要有三个明显的平台段，两次平台段下降分别是由于玻璃转化和结晶熔融，因此可以推断PVE 膜材为一种交联的半结晶聚合物，在整个温度区间依次有玻璃态、玻璃转化、半结晶橡胶态、结晶熔融和无定形橡胶态五种状态。其中玻璃转化和结晶熔融作为PVE 膜材的两大主转变，膜材的力学性能出现剧烈下降。

图1 中A，B，C，D，E和F点是判定PVE 膜材松弛转变的关键参考点。其中A点和D点为储能模量曲线上的特征点，A点是玻璃态和玻璃转化两段曲线的切线(A点上方的两条虚线)交点对应储能模量曲线上相同横坐标的点，储能模量曲线上下降最快的点即为D点；B点和E点为损耗模量曲线上的特征点，B点为曲线上的峰值点，而E点为波峰之后下降曲线出现明显转折的第一个点；C点和F点分别为损耗因子曲线上的两个峰值点。A，B，C和D点均是用于定义高聚物玻璃转化温度，在不同的研究范畴时可以选用的不同的衡量标准来确定膜材的玻璃转化温度Tg。在ISO标准中，一般取损耗模量的峰值即B点对应的温度定义玻璃转化温度Tg[22]。本文则考虑更通用的定义规则，取A点和D点对应的温度为玻璃转化温度区间的上下限，而不仅仅参考单一的温度作为膜材的性能参数。同样E点和F点被用于判定膜材结晶熔融温度区间的上下限，以此在整个温度区间为PVE 膜材各个状态温度区间划定量化指标。

图1 PVE膜材储能模量、损耗模量以及损耗因子随温度的变化曲线(10 Hz)Fig.1 Change curves of storage modulus,loss modulus and loss factor with temperature for PVE material(10 Hz)

在-35 ℃以下，PVE膜材表现为玻璃态，其模量可达到103MPa数量级，分子内部主要以较链段更小的链节、侧基等运动为主，分子构象改变的难易程度较大，在外力作用下分子内部通过改变键长和键角的形式储存能量。在-35～-15 ℃温度区间，PVE 膜材发生玻璃转化，分子内部自由体积增大使得链段的短程运动得以进行，分子构象改变的难度减小，储能模量出现剧烈下降，损耗模量和损耗因子依次达到峰值，膜材的黏性成分比例增大。这是由于在玻璃转化区间膜材中链节等运动形式不断转变为链段运动，两种运动形式同时存在。链节运动时分子链段运动被冻结，链节间作用等效为硬弹簧，而链段运动所需的外界能量较小，此时链段间作用可以等效为软弹簧。在玻璃转化区间链节运动对应的硬弹簧不断转变为链段运动对应的软弹簧；而相同变形量下硬弹簧储存的能量大于软弹簧储存的能量，在转变的过程中多余的能量会以热能的形式被耗散，因此，膜材的损耗模量和力学阻尼在玻璃转化温度区间处于较高的水平并达到峰值。

在-15～35 ℃温度区间，PVE 膜材处于半结晶橡胶态，膜材内部分结晶态分子受晶格能的限制仅能在固定的位置做热振动。并且半结晶橡胶态的储能模量相比于玻璃态下降了两个数量级。随着温度进一步提高，分子的热运动剧烈足以克服晶格能的限制。在35～65 ℃温度区间，结晶熔融的发生使得PVE 膜材的储能模量再一次下降约一个数量级，损耗因子再一次达到峰值。但值得注意的是，此时损耗模量并没有与玻璃转化区间相似达到峰值，而是与储能模量一同处于下降的趋势，只是损耗模量下降的幅度小于储能模量，使得损耗因子表现出上升并出现峰值。在65 ℃以上，膜材的性能几乎不受温度的影响，保持较稳定的状态。无定形橡胶态的PVE 膜材分子内部的运动形式统一为链段运动，并且由于分子的交联作用阻止了整个分子链发生流动，膜材的模量曲线表现为水平段而不出现再一次下降。

根 据SCHUSTER 等[10]对PVB 以 及evguard 和EVA SAFE G77两种不同品牌的EVA中间膜进行研究，发现PVB 膜材的玻璃转化温度区间在25～45 ℃，而两种EVA 膜材的玻璃转化温度区间分别是-40～-20 ℃和-35～-15 ℃。但PVB 膜材相比EVA 膜材没有结晶熔融现象的发生，EVA 膜材的结晶熔融温度区间分别为35～65 ℃和40～70 ℃。本研究中的PVE膜材在-35～-15 ℃发生玻璃转化，在35～65 ℃温度区间发生结晶熔融，与EVA 膜材具有相似松弛转变行为规律。

此外，频率对PVE 膜材的松弛转变行为也有一定的影响。不同频率下损耗模量和损耗因子随温度的变化曲线分别如图2和图3所示。可见，频率从0.1 Hz 提高至10.0 Hz，膜材的玻璃转化区间向右平移了约5 ℃，而结晶熔融温度区间几乎不受影响，依然处于35～65 ℃温度区间。从图2 和图3可以看出：在高温低频作用时，损耗模量和损耗因子随温度的变化曲线波动十分剧烈。这是由于高温低频作用相当于长时间的静载作用，高聚物膜材会发生明显的松弛现象，导致应力应变的相位差偏离正常值，进而出现曲线上的波动。而且损耗模量和损耗因子在玻璃转化峰值的左侧，频率升高使得两者有所下降，而在峰值的右侧出现相反的现象。不同频率下储能模量随温度的变化曲线如图4所示。从图4可以看出：提高频率使储能模量得到一定程度的增大，尤其是玻璃转化温度区间和无定形高弹态对频率的敏感性表现得更加显著。

图2 不同频率下损耗模量随温度的变化曲线Fig.2 Change curves of loss modulus with temperature at different frequencies

图3 不同频率下损耗因子随温度的变化曲线Fig.3 Change curves of loss factor with temperature at different frequencies

图4 不同频率下储能模量随温度的变化曲线Fig.4 Change curves of storage modulus with temperature at different frequencies

2.1.2 简单热流变行为规律

大量试验表明，温度和时间对高聚物的力学性能具有相同的影响效果，即时温等效原理[23]。长时间、低温下的高聚物性能可以通过在短时间、高温条件下观察，对试验的开展具有现实意义。在应用时温等效原理时，不同温度下的单根曲线能够向参考温度平移得到主曲线。

图5所示为PVE膜材储能模量主曲线。从图5可以看出：通过对PVE 膜材不同温度下的储能模量、损耗模量和损耗因子随频率变化曲线进行平移，PVE 储能模量相邻曲线具有很好的衔接性，故在试验条件下其符合简单热流变行为规律。主曲线的参考温度取0 ℃(即273.15 K)，各温度下的单根曲线首先由TRIOS 软件进行基于最小平方差的算法平移，但在保证衔接性的前提下相邻曲线的重叠程度具有较大的灵活性。为此进行主曲线的构造时除了考虑曲线的衔接性，还需要考虑其他的限制条件，对算法平移结果进行修正。

图5 PVE膜材储能模量主曲线Fig.5 Master curve of storage modulus for PVE material

基于分子运动原理，其运动的温度依赖性规律服从Arrhenius 方程(式(1))[24]。但该方程适用于高分子链的整链运动以及比链段小的链节、侧基等运动单元，对于运动单元为链段运动形式的高聚物，其温度依赖性规律可以由WLF 方程(式(2))描述。WLF 方程最初由WILLIAMS 等[25]通过大量试验数据总结得到，如今随着分子运动理论研究的深入，基于自由体积概念的WLF 方程理论推导已经较为成熟[12]。

其中：aT为各曲线向参考温度平移的水平位移因子；E为活化能，J/mol；R为气体常数，8.314 J/(mol·K)；Tref为参考温度，K；T为试验温度，K；C1和C2为WLF 方程中的系数。因此，考虑将这两个温度依赖性规律作为主曲线构造的另一个限制条件。手动对算法平移结果进行修正，以位移因子随温度的变化曲线为基准反馈手动平移结果的可行性，进而决定是否要进行再一次的手动平移，直至位移因子与温度之间的关系满足相应的温度依赖性规律。位移因子随温度的变化曲线如图6所示。从图6可知：位移因子与温度之间的关系以玻璃转化区间的温度为临界点，很好地吻合Arrhenius 方程和WLF方程，其拟合参数见表2。

图6 位移因子随温度的变化曲线Fig.6 Change curves of shift factor with temperature

表2 Arrhenius方程和WLF方程拟合参数Table 2 Fitting parameters of Arrhenius and WLF functions

2.1.3 黏弹性本构

在DMTA 试验中，根据损耗模量和损耗因子可以看出PVE 膜材表现出明显的黏弹性特性。而广义Maxwell 模型[16](图7)被广泛运用于描述小变形下的黏弹性行为，因此基于广义Maxwell模型建立PVE 膜材的黏弹性本构。该模型是由n个Maxwell元件和一个弹簧并联组成，其中的黏壶是黏弹性特性表达的重要元件。广义Maxwell模型的数学Prony级数的表达形式为

图7 广义Maxwell模型Fig.7 General Maxwell model

其中：E(t)为随时间变化的弹性模量；E∞为长期弹性模量；Ei为第i个Maxwell元件弹簧的弹性模量；τi=ηi/Ei为第i个Maxwell 元件的松弛时间；ηi为第i个Maxwell元件中黏壶的黏度。

由于DMTA 试验得到的是弹性模量均处于频域谱中，因此考虑使用FERRY[26]研究的经验公式(式(4))将频域谱中的储能模量和损耗模量转化为时域谱中的应力松弛模量。

式中：E(t)为时域谱中的应力松弛弹性模量；E′(ω)为频域谱中的储能模量；E″(ω)为频域谱中的损耗模量；ω为圆频率；t为应力松弛时间。基于式(4)和广义Maxwell模型得到的应力松弛模量以及拟合效果见图8，其拟合参数见表3。试验结果与拟合得到的广义Maxwell模型相关性系数达到0.999 91，表明广义Maxwell 模型能够很好地表征PVE 膜材黏弹性行为。

表3 广义Maxwell模型拟合参数Table 3 Fitting parameters of general Maxwell model

图8 时域谱中的应力松弛模量以及广义Maxwell模型拟合Fig.8 Stress relaxation modulus in time domain spectrum and fitting of generalized Maxwell model

2.2 PVE膜材松弛特性研究

由于高聚物的相对分子质量大，表现出明显的柔性，在外力作用下不能立即达到平衡状态；而且高聚物中还存在不同相对分子质量的分子链，进一步增加高聚物外力响应的时间相关性。本文从温度、应力水平对膜材蠕变的影响以及蠕变本构模型三个方面深入研究PVE 膜材长期的松弛特性。

2.2.1 温度对PVE膜蠕变的影响

温度从-40 ℃升高至80 ℃，跨越PVE 膜材热流变行为的特征温度点。0.5 MPa应力水平及不同温度下PVE膜蠕变曲线如图9所示。利用双坐标绘制PVE膜材在0.5 MPa应力水平以及不同温度条件下的蠕变曲线。从图9可知：随着温度上升，膜材的初始应变以及蠕变速率明显增加，膜材的抗蠕变能力随着温度升高而下降。在-40 ℃蠕变曲线几乎维持在零应变状态，PVE 膜材处于高模量的玻璃态，在外力施加的瞬间分子内通过改变键角和键长产生内应力与外力平衡，平衡响应几乎在外力施加瞬间完成。0 ℃时从DMTA试验结果分析可知，其经历了玻璃转化处于半结晶高弹态，膜材的抗蠕变性有所下降，在初始的几十秒出现明显的松弛现象，但后续应变约以10-6s-1的低应变速率增长。40 ℃时PVE 膜材发生结晶熔融，蠕变现象表现更加明显。80 ℃膜材的蠕变应变急剧增大，6 000 s时应变达到4.635，产生明显的变形。

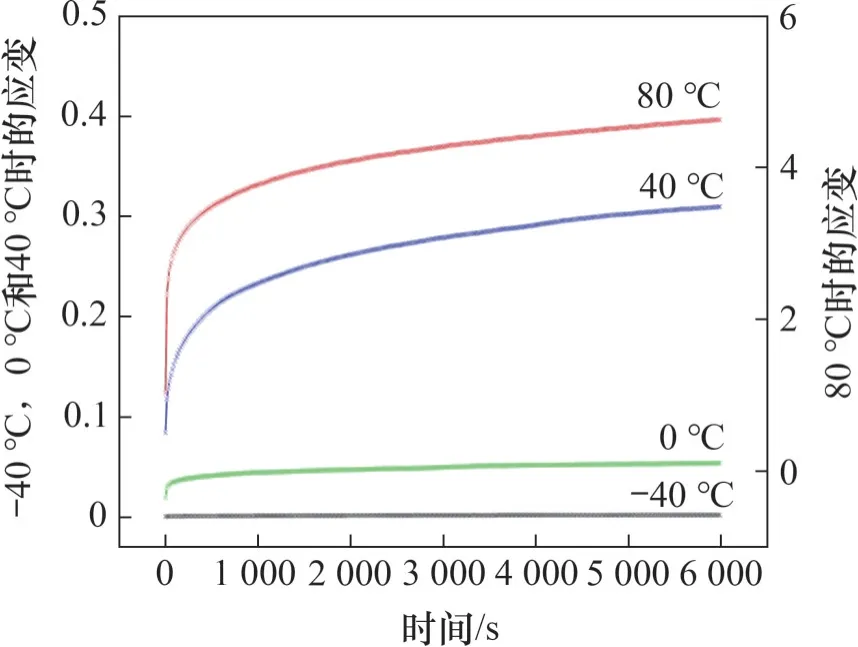
图9 0.5 MPa应力水平及不同温度下PVE膜蠕变曲线Fig.9 Creep curves under stress level of 0.5 MPa at different temperatures for PVE

2.2.2 应力水平对PVE膜蠕变的影响

应力水平会影响高聚物分子链段运动的位垒，其蠕变性能对不同的应力水平产生不同的响应特性。其中初始应变和蠕变增量作为膜材蠕变特性研究的两个重要的参数，前者体现膜材的瞬时刚度，后者表示膜材的抗蠕变性。不同温度下两种应力水平情况的蠕变特征值对比如图10 所示。在各温度下应力水平提高均会显著提高初始应变以及在6 000 s 时间内的应变增量(其中80 ℃及1.0 MPa 条件下试样样本的变形量过大而超出Q850 仪器的变形量程)，表明应力水平的提高能够使得PVE 膜材的蠕变现象更加明显且提高了蠕变速率。此外，从图10还可得出以下规律：

图10 不同温度下两种应力水平情况的蠕变特征值对比Fig.10 Comparison of creep characteristic values of two stress levels at different temperatures

1) 温度具有加剧应力水平对PVE膜材蠕变速率影响的效应。应力水平从0.5 MPa提高至1.0 MPa，-40 ℃、0 ℃和40 ℃温度条件下，6 000 s 应变增量分别为8.20×10-4，6.14×10-2和7.22×10-1。随着温度升高，同样应力水平提高的条件下相同时间内蠕变应变的增加表现得更加明显。

2) 应力水平对初始应变的影响具有非线性。应力水平线性增加提高至原来的两倍，-40、0 和40 ℃温度条件下初始应变分别提高至原来的2.40，4.03 和3.65 倍，表现出非线性影响效应；且PVE膜材的初始刚度随着应力水平提高而有所下降，表现出蠕变初始刚度的应力水平相关性。

3) 0 ℃温度条件相比于-40，40和80 ℃，PVE膜材在受外荷载作用时短期效应相比于长期效应更加明显。在-40，40 和80 ℃温度条件下，6 000 s的蠕变增量均显著高于初始应变，并且随着温度和应力水平提高，长期效应表现更加明显。然而在0 ℃温度条件下，蠕变增量却低于初始应变，且随着应力水平提高，短期效应的比例也随之提高，长期效应表现出的变形量相比于短期效应有所下降。

2.2.3 蠕变本构

描述蠕变的模型通常有Burgers 模型[27-28]、Findley幂法则[29]以及广义Kelvin-Voigt模型[30-31]。但Findley 幂法则基于试验曲线进行唯象拟合，模型参数不代表实际的物理意义。Burgers 模型又称为四元件模型，模型中的弹簧、黏壶和Kelvin 元件能在一定程度上反映高聚物的松弛特性，但其仅存在一个松弛机制，难以很好地描述内部存在多种分子的高聚物。广义Kelvin-Voigt 模型(图11)是对Burgers 模型进行改进以更好地描述高分子聚合物的蠕变特性。广义Kelvin-Voigt 模型由n个Kelvin元件和一个弹簧串联构成，在外力σ的作用下，整体应变为

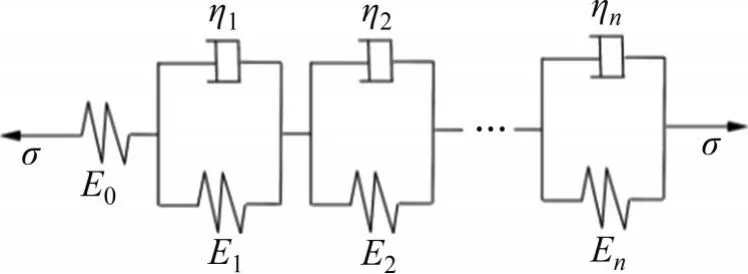
图11 广义Kelvin-Voigt模型Fig.11 General Kelvin-Voigt model

其中：σ为施加的应力水平；E0为代表膜材初始刚度的弹性模量；Ei为第i个Kelvin 元件中弹簧的弹性模量，τi=ηi/Ei为第i个Kelvin 元件的松弛时间；ηi为第i个Kelvin元件中黏壶的黏度。

基于PVE 膜材各温度和应力水平条件下的蠕变特性，对广义Kelvin-Voigt 模型进行训练。拟合结果表明广义Kelvin-Voigt 模型对蠕变特性具有很好的表征性，相关性系数均达到0.99 以上，其拟合结果见表4。

表4 各温度以及应力水平下广义Kelvin-Voigt模型拟合参数Table 4 Fitting parameters of general Kelvin-Voigt model under different stress levels at different temperatures

3 结论

1) PVE 膜材为一种交联的半结晶高聚物。在-50～120 ℃温度区间，其依次会有玻璃态、玻璃转化、半结晶橡胶态、结晶熔融和无定形橡胶态五种状态出现，其中在-35～-15 ℃温度区间发生玻璃转化，在35～65 ℃温度区间发生结晶熔融，模量分别有两个和一个数量级的下降。

2) 温度和时间对PVE 膜材储能模量具有相同的影响，其在试验条件下服从简单热流变行为规律，且Arrhenius和WLF方程能够分别描述玻璃转化温度以下和以上温度区间膜材温度和时间的关系。

3) 温度和应力水平均能使得PVE 膜材的蠕变现象更加明显。例如，在0.5 MPa应力水平下，温度从-40 ℃升高至80 ℃，100 min时的蠕变应变约提高了2 340倍。在40 ℃温度条件下，应力水平从0.5 MPa 提高至1.0 MPa，100 min 时的蠕变应变约提高了3.17倍。

4) 应力水平对初始应变的影响具有非线性。应力水平从0.5 MPa 提高至1.0 MPa，初始应变增幅超过100%；而且其初始刚度随着应力水平提高而有所下降，表现出蠕变初始刚度的应力水平相关性。

5) 广义Maxwell 模型和广义Kelvin-Voigt 模型均能很好地描述PVE 膜材的黏弹性行为和蠕变特性，为PVE 膜材在夹层玻璃中的应用和设计方法提供支撑。