竖向荷载作用下悬索桥内力计算研究★

马玉荣,李海霞

(安徽新华学院，建筑结构安徽省普通高校重点实验室，安徽 合肥 230088)

1 概述

桥梁设计软件的应用极大的解放了桥梁设计师的重复劳动，但复杂桥梁建模过程烦琐，耗时较长，一旦结构计算不收敛，模型检查的工作量巨大。因此很多学者在桥梁的内力计算方面做了很多研究[1-4]，试图弥补桥梁软件在桥梁设计中的不足。本文以日本关门桥为例，给出了悬索桥在竖向荷载作用下的内力计算方法，为今后悬索桥的设计计算及校核提供了快捷方法。

2 计算原理及应用

2.1 工程案例

日本关门桥简图如图1所示，1973年建造，总跨1 068 m，(178+712+178)m三跨钢桁架悬索桥，塔高133.8 m，边跨长167.2 m，梁高9 m，宽28.5 m，Iz=2.916 m4,主缆垂度64 m，边缆垂度3.909 m，缆索截面积As1=0.599 m2(2×154×91φ5.04 mm)，缆索和吊索的材料的弹性模量E=2×105MPa，主梁设计时恒载为120.86 kN/m，风载为18.85 kN/m，地震荷载为4.57 kN/m，主缆：荷载25.66 kN/m，风载3.02 kN/m，地震荷载1.23 kN/m[5]。

2.2 计算方法

本文计算内容所取的计算结构简图如图2所示。在图2所示结构中，在Fkp,qkp作用下(缆索和吊索上无外荷载)，每根吊索所产生的拉力相同。图2所示体系，用力法求解时为一次超静定，取力法基本体系如图3所示。

该桥的吊索间距d=8.9 m，每缆下79根吊索，索直径为φ60 mm高强度钢绳索。每吊杆可承受拉力4 524 kN(As2×1 600 MPa,As2为吊索截面面积)，EsAs2=EI/500,一根缆索可承受拉力447 200 kN(As1×1 600 MPa)，EsAs1=EI/5.2，桁架梁用16号锰钢焊成，双排桁架，每一桁架可承受弯矩=220 320 kN·m。由索l=712 m，f=64 m，f/l=1/11.125，则缆索方程为：

由此方程可算出：

∂Δy=Δyi+1-yi=0.08。

Δlmax=9.444 m。

∑y=y0+∑yi=1 918 m。

∑Δl3=61 890 m。

其中,Δli为每段缆索长度；∑y为所有吊索总长。

用力法进行求解,一次超静定力法方程为:

δ11X1+Δ1P=0。

1)δ11系数项由三部分组成:

2)Δ1p常数项由两部分组成:

由于缆索和吊索自重产生的Δ1p非常微小,不计入Δ1p的计算。Δ1p由梁上作用荷载和梁的自重产生。

qk=10.5+(120.86+18.85+4.57)/2=82.72 kN/m。

其中，αl为Fkp在梁上的作用位置。

吊索安全系数计算:

最长吊索产生最大吊索拉力(以此根吊索为强度校核依据)。

FTmax=X1+最长吊索自重=741.39+14.04=755.43 kN。

缆索安全系数计算:

缆索内力由吊索拉力产生的缆索内力两部分产生,最大缆索内力产生在最长吊索处,即缆索端部(以此处为缆索强度校核依据)。

由吊索产生的缆索端部内力:

q0=缆索自重+索上风载+索上地震荷载=25.66+3.02+1.23=29.91 kN。

加劲梁安全系数计算:

X1=738.835 3。

q1=0.285 2 kN/m(↑)。

则梁的最大弯矩值为：

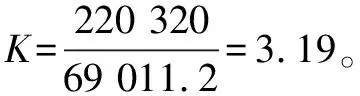
2.3 计算结果比对

本案例同时采用通用有限元程序Midas/Civil计算数据及文献[5]中记载的设计此桥的桥梁设计规范数据与该文的计算结果进行对比分析(见表1)。

表1 桥梁主要构件的安全系数

文献[5]中记载,对于建在海边江河海港上的、地震多发区的悬索桥,设计时安全系数应取的偏大。因吊索直径远小于缆索直径,在风雨作用下吊索易于发生颤振现象,故安全系数大于缆索的安全系数。通过表1数据的对比分析,可知该文计算结果是正确的。

3 结论

1)运用本文的方法对已建成的如本关门桥进行校核,计算结果与Midas/Civil结构分析软件得出的数据及桥梁设计规范数据对比表明:该文提供的计算方法正确,本文计算方法可为悬索桥设计及校核提供新的而且比较快捷的方法,可以与软件计算互为校核。

2)文中提出悬索桥内力计算方法,可以编写成计算机程序,将实现更加快捷的桥梁设计和校核。