爆炸荷载下张拉膜结构的动力响应研究

杨晨瑶，马佳文，王 浩，马小川，薛恺文

(中国矿业大学力学与土木工程学院，江苏 徐州 221116)

0 引言

近年来爆炸事故时有发生，爆炸源引起的建筑物倒塌和各类残片是造成人员伤亡与财产损失的主要原因。当前对爆炸残片及冲击波作用下的结构失效机理研究主要集中在传统刚性结构，对膜结构的相关研究鲜有涉及。膜结构[1-2]可通过发生大变形耗散能量，在爆炸荷载作用下有独特的优势。由于爆炸冲击荷载的特殊性、膜材建筑瞬间发生大变形等原因，膜结构在爆炸荷载下的结构特性与静力作用下的结构特性有着明显差异，传统的静力学计算方法不再适用。因此，本文通过数值模拟分析爆炸载荷作用下膜结构的动力响应过程，阐述膜结构的抗冲击机理。

1 结构试件设计

1.1 张拉膜结构设计

建立一种张拉膜结构的有限元模型试件，试件尺寸为4 m(长)×4 m(宽)×0.001 m(厚)，质量密度为1 350 kg/m3，质量为均匀分布。弹性模量E1=691 MPa，E2=601 MPa，泊松比为0.3，剪切模量G12=20 MPa，G13=20 MPa，G23=20 MPa。热膨胀系数alpha=6×10-6，膨胀类型为各项同性。试件具体组成情况见表1。

表1 试件参数

1.2 弹片设计

建立一种半圆球形空心有限元壳模型试件，模拟爆炸产生的弹片，模型试件简化为刚体，其半径为R=0.3 m。弹片模型初始位置位于张拉膜结构中心点垂直距离1 m处，并设置弹片模型基础速度为Z方向100 m/s，随后控制炸药TNT当量为0.1 kg，改变弹片速度为90 m/s，80 m/s，70 m/s，60 m/s，50 m/s，得出弹片不同速度时张拉膜结构的动力响应并进行分析。

1.3 网格单元划分

张拉膜结构取网格单元的整体近似比例为0.1，残片模型取网格单元的整体近似比例为0.05。张拉膜结构与弹片装配模型见图1。

1.4 相互作用与边界条件

设置相互作用时间长度为0.01 s，无时间缩放。线性体积黏性参数为0.06 s，二次体积黏性参数为1.2 s。

入射的冲击波采用ABAQUS内置的CONWEP模型，CONWEP模型考虑空气的可压缩性与轻质的特点，忽略了空气的刚度与惯性效应，因此使用它进行空中爆炸分析时不用为空气介质建模，仅需结构模型参与爆炸响应计算即可，这样在较高的精度范围内，大大节省了爆炸分析的计算量。在ABAQUS中，只需要定义起爆点、结构上的爆炸载荷作用面、爆炸类型和炸药的TNT当量即可，内置的CONWEP模型可以据此计算出爆炸载荷曲线中的载荷到达时间、最大超压、超压时间、指数衰减因子等参数。

设置炸药TNT当量为0.1 kg,引爆时间为0时刻，无大小缩放。设置弹片动力显示力学约束为运动接触法，并设置为有限滑移。张拉膜的边界约束为完全固定。

1.5 预张力施加

通过降温法对平面张拉膜结构施加预应力，计算公式如下：

其中，Δt为降温法温度下降值；T为设定的膜面初始预应力；E为膜材弹性模量；η为膜材热膨胀系数；t为膜材厚度。

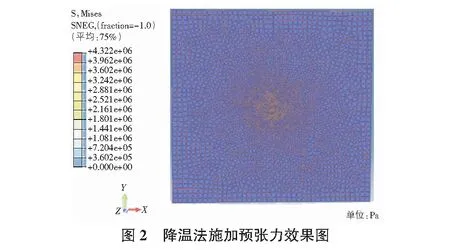
降温法施加预张力过程：设置张拉膜的热膨胀系数E为6×10-6，设初始状态温度为0 ℃，分析步状态温度为-800 ℃,即降温800 ℃，膜材厚度t=0.001 m,降温后施加的预张力可达到4.322 MPa。降温法施加预应力效果图见图2。

2 冲击波荷载作用下膜结构动力响应

2.1 模型概况

建立一种空气冲击波相互作用，炸药TNT当量设置为0.1 kg，位于膜中心点垂直距离为1 m处。张拉膜结构的模型参数在第1节中已有介绍。

2.2 模拟云图分析

1)位移应变分析。位移分布云图见图3。

由图3可见张拉膜随时间向外隆起，其变形从膜的中间向四周逐渐减小，其位移最大值为0.335 6 m，在膜的中心位置。

2)应力状态分析。对模型的应力分布图(如图4所示)进行分析，模型的应力变化可以分为前期和后期。通过ABAQUS提供的标注功能我们发现，张拉膜结构在冲击波作用下，膜结构的应力最大值一直处于膜的中心位置，而应力最小值一直处于膜的四个角上，应力的最大值为16.76 MPa，最小值为0.128 7 MPa。在冲击波作用的前期，膜上应力分布与应变分布类似，从中心位置向四周逐渐减小，其应力等势线呈圆形，从中间向四周逐渐扩散。而当应力等势线达到张拉膜边界时，膜的应力状态开始进入后期。这时，除了膜的中心位置，膜的四周也对称出现了应力集中的现象。

根据膜在冲击波作用下的应力和应变情况，我们发现膜面出现了多处的应力集中现象，可能会导致膜面的结构性破坏，在实际设计过程中可以对这些位置进行加固。

3 弹片作用下膜结构动力响应(v=50 m/s)

1)位移应变分析。

张拉膜受弹片作用的位移云图见图5。

由图5可以得到，弹片入射的地方，膜面最大位移达到1.0 m，随着距离入射点距离的增大，位移值也随之减小，最小位移值在膜角点，数值为0。

2)应力状态分析。

张拉膜受弹片作用的应力云图见图6。

由图6可以看出当弹片入射在膜中心处时，膜面应力变化规律类似于位移云图，位移最大处应力也为最大值，即弹片入射的地方，膜面最大应力达到128.55 MPa，随着距离入射点距离的增大，应力值也随之减小，最小应力值在膜角点，为7.672 MPa。

而通过对比图7，图8的前后变化过程可以发现，应力变化云图呈现出明显“十字形”增长规律，直到整个膜面各个位置达到其应力峰值。

4 冲击波与弹片耦合作用下膜结构动力响应

4.1 改变弹片速度的分析结果

4.1.1 张拉膜应力云图

设定TNT炸药包的当量m=0.1 kg并保持不变，改变弹片速度,分别为100 m/s，90 m/s，80 m/s，70 m/s，60 m/s，50 m/s，导出不同弹片速度时张拉膜结构的动力响应并进行分析。分析步结束时膜结构变形后的应力见云图9。

4.1.2 张拉膜最大位移

改变弹片速度，分别为100 m/s，90 m/s，80 m/s，70 m/s，60 m/s，50 m/s，导出不同弹片速度时张拉膜结构节点A的最大位移情况并进行对比(见表2)。

表2 不同弹片速度下张拉膜结构节点A的最大位移

可见在时间0.01 s内，随着弹片速度的等差增加，张拉膜结构上节点A的最大位移也呈现几乎等差的增加(见图10)。

4.1.3 张拉膜最大主应变

改变弹片速度，分别为100 m/s，90 m/s，80 m/s，70 m/s，60 m/s，50 m/s，导出不同弹片速度时张拉膜结构节点A的最大主应变(见图11)。在0.002 s时刻，弹片与冲击波相互耦合作用在张拉膜结构上产生第一次最大主应变峰值，在0.004 s时刻，产生第二次最大主应变峰值，结果表明，两者耦合比单一荷载作用释放的能量效应更明显。

4.1.4 张拉膜的应变能

改变弹片速度，分别为100 m/s，90 m/s，80 m/s，70 m/s，60 m/s，50 m/s，得出不同弹片速度时张拉膜结构的应变能(见表3)。

表3 不同弹片速度下张拉膜结构的应变能

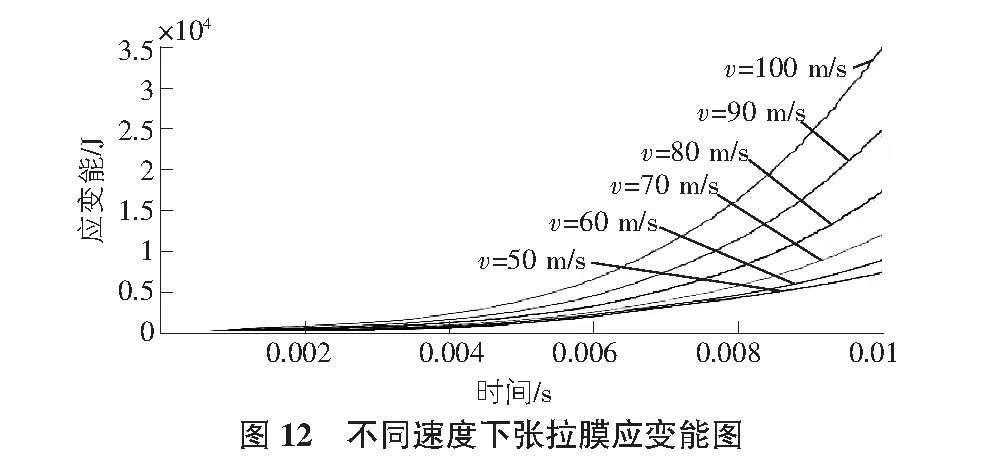
由表3中数据易得，随着时间的增加张拉膜结构的应变能呈指数上升，且随着弹片速度的增加应变能逐渐增加。不同速度下张拉膜应变能图如图12所示。

4.2 改变炸药当量的分析结果

4.2.1 张拉膜应力云图

设定弹片速度v=100 m/s并保持不变，改变TNT炸药的当量，分别为0.5 kg，1 kg。得到不同炸药当量时张拉膜结构的动力响应。膜结构变形后的应力云图如图13，图14所示。

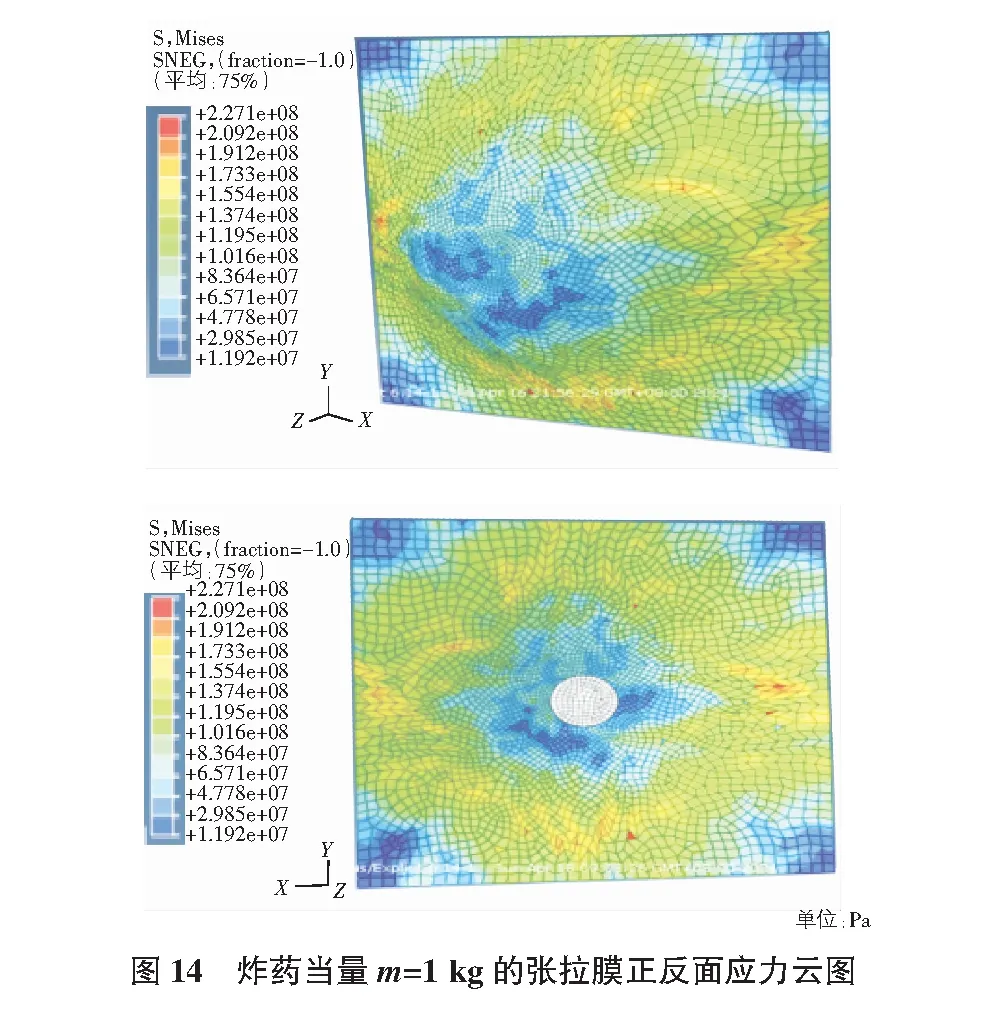
通过观察爆炸荷载作用下张拉膜的应力云图可得，炸药当量m=0.1 kg时，冲击波和弹片全过程同时作用在膜结构上；炸药当量m=0.5 kg时，在冲击波和弹片联合作用条件下，形成弹片-冲击波-弹片的接触模式，冲击波作用时间大于弹片接触时间，两者对结构具有一定的耦合效应。冲击波作用主要引起膜面的整体挠曲大变形，而弹片穿膜为局部效应，当弹片速度非常高且弹片距离膜面较近时，极易在接触区形成大破口；炸药当量m=1 kg时，冲击波冲击作用强烈导致弹片未与膜面接触。

4.2.2 张拉膜最大位移

炸药当量m=0.5 kg时，膜结构受到爆炸荷载的冲击破坏，取弹片与张拉膜接触边缘上的一个节点为观测对象；炸药当量m=1 kg时，膜结构尚未破坏，取膜中心一点为观测对象(见图15)。通过分析节点的最大位移时程曲线，总结膜结构在冲击波与弹片耦合作用下的变形位移特征(见图16)。

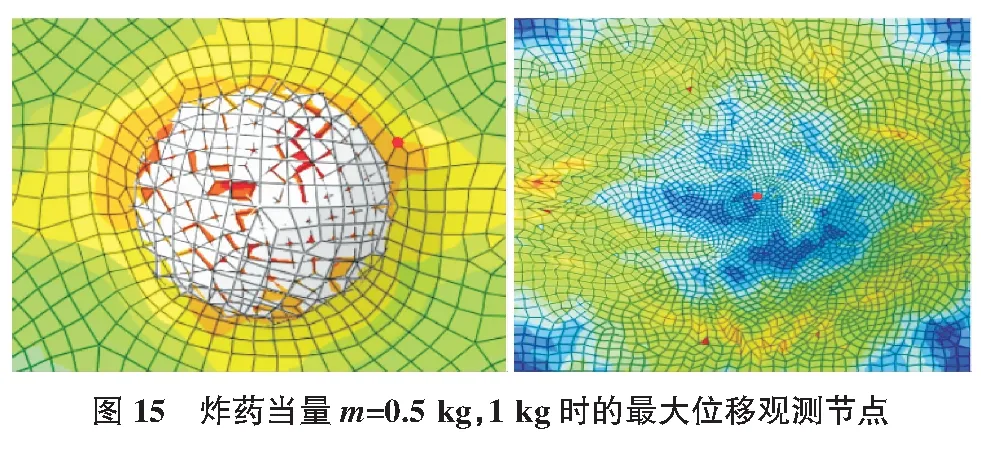
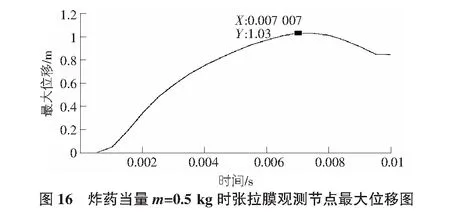
观察m=0.5 kg时观测节点位移曲线可见，节点位移在0.001 s左右有突变，突变后位移不断增加至峰值1.03 m，随后衰减至0.8 m保持不变。这是因为0.001 s之前弹片与膜结构接触产生一小段位移，随着冲击波的不断扩散，冲击波对膜结构位移的作用已超过弹片对膜结构的位移作用，致使0.001 s附近观测节点的位移突变。在0.001 s至节点位移达到峰值时段内，弹片与膜结构无接触，冲击波是使膜结构发生位移的唯一因素。0.001 s～0.009 s 时段内膜结构在冲击波作用下发生振动，位移达到峰值然后逐渐减小。当膜结构的位移减小至0.9 m时，弹片撞击膜结构致使张拉膜破坏，膜结构的失效导致最终的位移为0.9 m并保持不变。当量m=1 kg时张拉膜观测节点最大位移图见图17。

炸药当量m=1 kg时的节点位移曲线与m=0.5 kg时曲线走向相近，不同的是m=1 kg时弹片与膜结构仅发生位移突变前的一小段位移。当冲击波的作用成为膜结构发生位移的主导因素后，弹片并未与膜结构接触，膜结构未受弹片冲击而破坏，因此0.01 s时膜结构的位移仍在减小。

4.2.3 张拉膜最大主应变

与爆炸荷载下张拉膜的最大位移分析类似，炸药当量m=0.5 kg时，取弹片与张拉膜接触边缘上的一个单元为观测对象；炸药当量m=1 kg时，膜结构尚未破坏，取膜中心一单元为观测对象。通过分析观测单元的最大主应变曲线(见图18，图19)，总结膜单元在冲击波与弹片耦合作用下的应变特征。

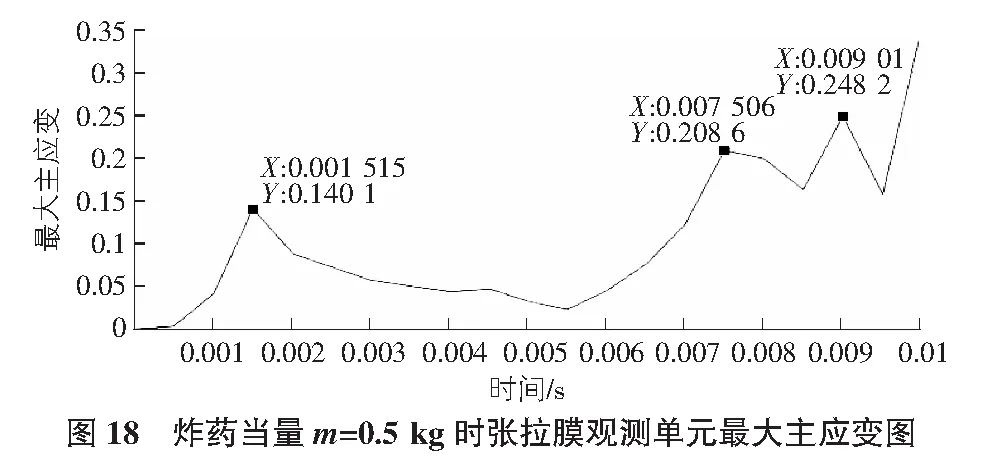
在0.002 s左右，两种当量的炸药产生的冲击波均达峰值应变，峰值应变的增长倍数小于当量的增长倍数。由于张拉膜中心的应力向四周呈“十字形”扩散，中心单元的应力衰减，膜面应变降到最低点。随着膜四周应力达到峰值，应力波的中心由四周逐渐向中心转移，使得中心的最大主应变再次增大，而应变的增幅与炸药当量有关。所以在这种应力波的传播机制下，膜应变呈现周期性的“增大-减小-再次增大”的现象。m=0.5 kg时，弹片在0.009 5 s左右与张拉膜碰撞使得膜结构破坏，破口周围的膜应变随时间呈线性增长趋势。

4.2.4 张拉膜的应变能

对比仅有冲击波作用的张拉膜应变能(如图20所示)和相同炸药当量下的冲击波-弹片耦合作用下的张拉膜应变能，可以得到炸药当量m=1 kg时，冲击波作用致使张拉膜产生的应变能539.1 kJ占总应变能553.5 kJ的92%左右；m=0.5 kg时，仅有冲击波作用的应变能更是超过了耦合作用下的应变能。可见，冲击波作用下产生的应变能远远超过弹片作用下的应变能。

5 总结与展望

本文利用ABAQUS有限元软件建立了一种张拉膜结构的有限元模型，模拟爆炸环境下张拉膜结构在遭受冲击波与弹片，以及其耦合作用下的一系列动力响应。并分别改变弹片速度和炸药TNT当量，可以得出：

1)张拉膜结构在受到冲击波作用后，其膜中心处和膜四周会对称出现应力集中现象。在设计抗爆膜时可以对这些部位进行加厚处理。

2)张拉膜受弹片冲击作用的应力变化云图呈现出“十字形”增长规律，直到整个膜面各个位置达到其应力峰值。膜面中心点应力变化剧烈，膜面变形振动频率大，应力曲线存在“增大-应力减小-再次增大”的现象。对角线处膜面应力变化初始较为平缓，后期增长速率变快，曲线斜率也明显变大。而远离膜中心的“十字形”棱上观测点初始阶段应力增长较快，后期增长速率开始减缓。有关“十字形”应力影响区的产生机理以及传播规律待我们下一步进行研究，这与我们研究的膜结构动力响应问题是密切相关的。

3)在冲击波-弹片耦合作用下，随着弹片速度的等差增加，张拉膜结构上节点的最大位移也呈现几乎等差的增加，且弹片与冲击波两者耦合作用下比单一荷载作用释放的能量效应更明显。随着时间的增加张拉膜结构的应变能呈指数上升，且随着弹片速度的增加应变能逐渐增加。

4)冲击波作用主要引起膜面的整体挠曲大变形，而弹片穿膜为局部效应，当弹片速度非常高且弹片距离膜面较近时，极易在接触区形成大破口。膜结构在冲击波作用下产生的应变能远远超过弹片作用下的应变能。

由于试验的分析时长仅为0.01 s，对于这一时间点之后的动力响应情况没有分析，故随后的试验可以考虑延长作用时间。并尝试改变膜结构的相关材料参数，做进一步膜结构抗爆炸现象的力学行为分析。

最后，上述模型并不能完全等同于实际膜的结构设计，实际膜结构例如充气膜结构的内部气压等参数也会对抗爆炸性能产生影响。并且本文模拟的张拉膜结构较为理想，没有考虑不同方向上的弹性模量与剪切模量的差异，这些条件都可能与实际结构有所区别。对于膜结构的抗爆炸性能的研究还需要更加具体深入的模拟与分析。